[python] การสร้างจำลองข้อมูลเป็นกลุ่มก้อนขึ้นมาเพื่อใช้ทดสอบการเรียนรู้ของเครื่อง
เขียนเมื่อ 2016/11/27 18:45
แก้ไขล่าสุด 2022/07/21 15:26
ก่อนหน้านี้ได้เขียนถึงการสร้างแบบจำลองสำหรับวิเคราะห์การถดถอยโลจิสติกไป https://phyblas.hinaboshi.com/20161103
ตัวอย่างในนั้นใช้ข้อมูลที่มีแค่สองมิติ (แกน x และ y) ตลอด แต่ว่าคลาสที่สร้างขึ้นตอนท้ายสุดนั้นถูกสร้างเผื่อไว้ให้สามารถใช้ได้กับข้อมูลที่มิติเป็นเท่าไหร่ก็ได้
ดังนั้นจึงอยากทดสอบกับตัวอย่างที่มีหลายมิติมากขึ้นไปสักหน่อย
มอดูล sklearn นั้นนอกจากจะมีคำสั่งมากมายที่ช่วยในคำนวณสำหรับการเรียนรู้ของเครื่องแล้ว ก็ยังมีความสามารถในการสร้างข้อมูลขึ้นมาเพื่อใช้ทดสอบด้วย ในครั้งนี้เราจะลองใช้ดู
ภายในมอดูลย่อย datasets ของ sklearn มีฟังก์ชันอยู่หลายชนิดที่ใช้สำหรับจำลองข้อมูลเพื่อนำมาใช้ทดสอบการเรียนรู้ของเครื่อง ครั้งนี้ที่จะใช้คือฟังก์ชัน make_blobs ซึ่งใช้สร้างชุดข้อมูลซึ่งมีการกระจายเป็นกระจุกแบบเกาส์ขึ้นมาเป็นกลุ่มๆ
อธิบายด้วยคำพูดอาจนึกภาพตามยาก มาดูตัวอย่างเพื่อให้เห็นภาพดีกว่า
สมมุติเราต้องการสร้างชุดข้อมูลสองมิติซึ่งมีจำนวนข้อมูลพันตัว และมีการแบ่งกลุ่มออกเป็น ๕ กลุ่มก็สามารถเขียนได้แบบนี้
ในที่นี้ n_samples คือจำนวนข้อมูลที่ต้องการ n_features คือจำนวนมิติของข้อมูล (จำนวนตัวแปรต้น) และ centers
ฟังก์ชัน datasets.make_blobs ในที่นี้จะคืนค่ามา ๒ ตัว ซึ่งในที่นี้เก็บในตัวแปร X และ z
ตัวแรก X คือข้อมูลตัวแปรต้น เป็นอาเรย์ที่มีจำนวนหลักเท่ากับ n_features และจำนวนแถวเท่ากับ n_samples
ส่วนตัวที่สอง z คือหมายเลขแสดงกลุ่ม จะเป็นเลขจำนวนเต็มไล่ตั้งแต่ 0 ไปจนถึงจำนวนที่ระบุไว้ที่ centers ในที่นี้ใส่ไว้ 5 ก็จะได้เลข 0 ถึง 4
ลองดูค่า X และ z ที่ได้มา
ได้
หมายเลขใน z จะสัมพันธ์กับตำแหน่งที่ระบุใน X โดยหมายเลขเดียวกันจะมีค่า X ใกล้เคียงกัน
ลองนำมาวาดแผนภาพการกระจายเพื่อดูว่าค่าของแต่ละกลุ่มเป็นอย่างไรบ้าง

จะได้แบบนี้คือเป็นกลุ่มก้อน ๕ กลุ่ม ภาพที่ได้อาจต่างกันออกไปขึ้นอยู่กับว่าสุ่มได้แบบไหน ลองทำซ้ำดูหลายๆครั้งได้จะเห็นภาพและเข้าใจฟังก์ชันนี้มากขึ้น
ถ้าลองเปลี่ยน n_features เป็น 3 ก็จะได้ข้อมูลเป็นสามมิติ
ลองสร้างข้อมูลสามมิติซึ่งแบ่งเป็น ๗ กลุ่มจากนั้นก็วาดแผนภาพการกระจายในสามมิติด้วย mpl_toolkits.mplot3d
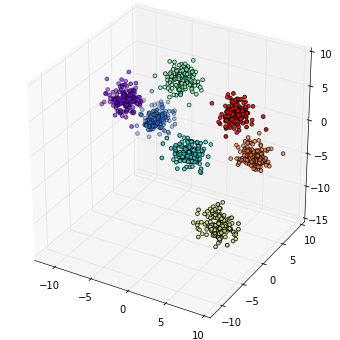
***เรื่องของการใช้ mpl_toolkits.mplot3d เพื่อวาดภาพสามมิตินี้ยังไม่เคยเขียนลงบล็อกนี้แต่ขอนำมาใช้ก่อน ไว้มีโอกาสจะเขียนถึงเพราะเป็นเรื่องที่สำคัญต้องใช้งานเยอะอยู่
จะเพิ่ม n_features เป็นกี่มิติก็ได้ แต่ถ้า 4 ขึ้นไปคงจะไม่สามารถวาดแผนภาพการกระจายแสดงให้เห็นได้แล้ว เข้าสู่โลกที่สามัญสำนึกของมนุษย์ยากจะจินตนาการถึง แต่ถึงอย่างนั้นข้อมูลทั่วไปก็มักจะมีหลายมิติ จะไม่พูดถึงคงไม่ได้ เพียงแต่จะไม่สามารถวาดแผนภาพง่ายๆให้ดูได้
นอกจากนี้สามารถปรับอะไรได้อีกหลายอย่าง สรุปพารามิเตอร์ที่ใส่ได้มีดังนี้
ถ้าต้องการให้ข้อมูลมีการกระจายมากขึ้นก็อาจปรับค่า cluster_std ให้สูงขึ้น แต่ถ้ามากไปแต่ละกลุ่มก็จะปนๆกันได้ง่าย
หรือถ้าลด center_box ให้ขอบเขตการสุ่มใจกลางแต่ละกลุ่มแคบลงก็จะเกิดการปนกันได้ง่ายเช่นกัน
ข้อมูลที่มีการปนกันแยกออกยากในบางส่วนก็อาจใช้เป็นตัวอย่างการเรียนรู้ในกรณีที่มีความไม่แน่นอนของข้อมูลสูงได้ ขึ้นอยู่กับการใช้งาน
ส่วน random_state นั้นคล้ายกับ np.random.seed ของ numpy คือเอาไว้ใช้เมื่อต้องการให้สุ่มได้ข้อมูลชุดเดิมๆ เช่นถ้าใส่ random_state=100 แล้วลองรันซ้ำๆดูไม่ว่ากี่ครั้งก็จะได้เท่าเดิม แต่ถ้าลองเปลี่ยนเป็น random_state=101 จะได้ค่าที่ต่างไปอีกค่า แต่ถ้าไม่ใส่อะไรจะเท่ากับเป็น Nonoe ก็จะสุ่มได้ข้อมูลต่างกันไปตลอดหมดทุกครั้ง
ตอนนี้ได้รู้วิธีสร้างข้อมูลทดสอบขึ้นมาแล้ว ต่อไปลองนำมาใช้เป็นตัวอย่างการทดสอบการวิเคราะห์การถดถอยโลจิสติก
เพียงแต่ว่าตอนนี้แบบจำลองที่ได้ทำขึ้นนั้นใช้ได้แค่สำหรับการแบ่งกลุ่มเป็นสองกลุ่ม ดังนั้นใช้ centers=2 ซึ่งจะได้ z เป็นเลข 0 หรือ 1 สำหรับแบบจำลองการวิเคราะห์การถดถอยโลจิสติกแบบที่แบ่งข้อมูลเป็นหลายกลุ่มนั้นจะพูดถึงในโอกาสต่อไป
ในที่นี้จะใช้แบบจำลองวิเคราะห์การถดถอยโลจิสติกที่มีการปรับมาตรฐานที่เขียนถึงไว้ใน https://phyblas.hinaboshi.com/20161124
เพื่อเป็นการประหยัดพื้นที่ จะไม่เขียนส่วนนิยามคลาสในหน้านี้ซ้ำ ให้นำส่วนที่นิยามฟังก์ชัน sigmoid กับคลาส ThotthoiLogistic จากในหน้านั้นมาใช้
มีสรุปลงเอาไว้ใน github คัดลอกจากในนี้มาได้ https://github.com/phyblas/rianrupython/blob/master/kanrianrukhongkhrueang/thotthoi_logistic_2.py
จากนั้นจึงต่อด้วยโค้ดต่อไปนี้ ลองเริ่มจากแบบสองมิติซึ่งสามารถเห็นภาพได้ง่ายกันก่อน
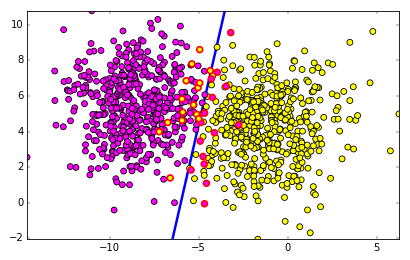
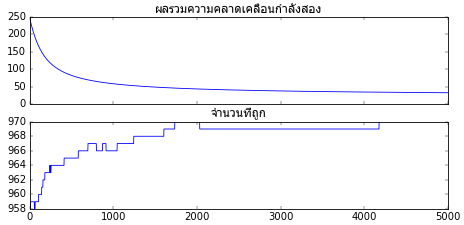
ถ้ากลุ่มก้อนมีการซ้อนทับกันแบบที่เห็นนี้ไม่ว่าจะเรียนรู้กี่ครั้งก็ไม่มีทางทายได้ถูกทั้งหมด แต่ถึงอย่างนั้นการเรียนรู้ก็ไปในทิศทางที่ทำให้จำนวนที่ทายถูกมีมากที่สุดเท่าที่จะทำได้
กรณีปัญหาแบบนี้เราอาจทำได้แค่หาความน่าจะเป็นที่จะอยู่กลุ่มนั้นๆเท่านั้น
เดิมทีตอนที่เราหาว่าเป็นกลุ่ม 0 หรือ 1 เราทำการคำนวณความน่าจะเป็นด้วยฟังก์ชันซิกมอยด์ด้วยเมธอด ha_sigmoid จากนั้นเมธอด thamnai ก็นำค่าไปใช้โดยดูว่าถ้าสูงกว่า 0.5 ก็ตัดเป็น 1 ถ้าต่ำกว่าก็ตัดเป็น 0
ดังนั้นแทนที่เราจะเอาค่าจากเมธอด thamnai ถ้าคำนวณค่าจากเมธอด ha_sigmoid ก็จะได้ค่าความน่าจะเป็นที่จะอยู่ในกลุ่ม 1
ลองวาดแผนภาพไล่สีแสดงความน่าจะเป็นดู
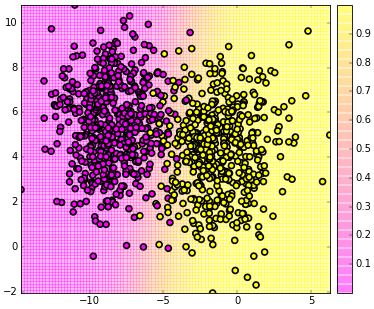
ต่อมาคราวนี้ลองใช้กับข้อมูลสามมิติดูบ้าง
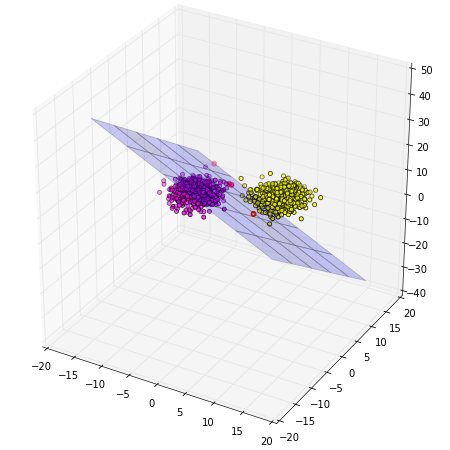
กรณีสามมิตินั้นแทนที่จะใช้แค่เส้นเป็นตัวคั่นก็ต้องเปลี่ยนเป็นใช้ระนาบในการคั่นแทน
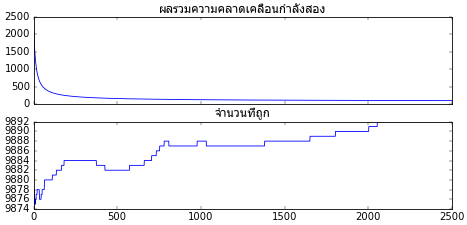
สุดท้ายลองกับห้ามิติดู คราวนี้มิติมากกว่าสามจึงทำเป็นภาพไม่ได้ ได้แค่ดูผลว่าค่าความคลาดเคลื่อนลดลงและจำนวนที่ถูกมากขึ้นเท่านั้น
อาจลองเปลี่ยนค่าต่างๆแล้วทดสอบแต่ละกรณีดูไปเรื่อยๆ
เท่านี้ก็จะเห็นได้ว่าแบบจำลองการวิเคราะห์การถดถอยโลจิสติกที่สร้างขึ้นนั้นสามารถใช้ได้ในข้อมูลที่มีตัวแปรต้นกี่ตัวก็ได้
ตัวอย่างในนั้นใช้ข้อมูลที่มีแค่สองมิติ (แกน x และ y) ตลอด แต่ว่าคลาสที่สร้างขึ้นตอนท้ายสุดนั้นถูกสร้างเผื่อไว้ให้สามารถใช้ได้กับข้อมูลที่มิติเป็นเท่าไหร่ก็ได้
ดังนั้นจึงอยากทดสอบกับตัวอย่างที่มีหลายมิติมากขึ้นไปสักหน่อย
มอดูล sklearn นั้นนอกจากจะมีคำสั่งมากมายที่ช่วยในคำนวณสำหรับการเรียนรู้ของเครื่องแล้ว ก็ยังมีความสามารถในการสร้างข้อมูลขึ้นมาเพื่อใช้ทดสอบด้วย ในครั้งนี้เราจะลองใช้ดู
ภายในมอดูลย่อย datasets ของ sklearn มีฟังก์ชันอยู่หลายชนิดที่ใช้สำหรับจำลองข้อมูลเพื่อนำมาใช้ทดสอบการเรียนรู้ของเครื่อง ครั้งนี้ที่จะใช้คือฟังก์ชัน make_blobs ซึ่งใช้สร้างชุดข้อมูลซึ่งมีการกระจายเป็นกระจุกแบบเกาส์ขึ้นมาเป็นกลุ่มๆ
อธิบายด้วยคำพูดอาจนึกภาพตามยาก มาดูตัวอย่างเพื่อให้เห็นภาพดีกว่า
สมมุติเราต้องการสร้างชุดข้อมูลสองมิติซึ่งมีจำนวนข้อมูลพันตัว และมีการแบ่งกลุ่มออกเป็น ๕ กลุ่มก็สามารถเขียนได้แบบนี้
import numpy as np
from sklearn import datasets
X,z = datasets.make_blobs(n_samples=1000,n_features=2,centers=5)
from sklearn import datasets
X,z = datasets.make_blobs(n_samples=1000,n_features=2,centers=5)
ในที่นี้ n_samples คือจำนวนข้อมูลที่ต้องการ n_features คือจำนวนมิติของข้อมูล (จำนวนตัวแปรต้น) และ centers
ฟังก์ชัน datasets.make_blobs ในที่นี้จะคืนค่ามา ๒ ตัว ซึ่งในที่นี้เก็บในตัวแปร X และ z
ตัวแรก X คือข้อมูลตัวแปรต้น เป็นอาเรย์ที่มีจำนวนหลักเท่ากับ n_features และจำนวนแถวเท่ากับ n_samples
ส่วนตัวที่สอง z คือหมายเลขแสดงกลุ่ม จะเป็นเลขจำนวนเต็มไล่ตั้งแต่ 0 ไปจนถึงจำนวนที่ระบุไว้ที่ centers ในที่นี้ใส่ไว้ 5 ก็จะได้เลข 0 ถึง 4
ลองดูค่า X และ z ที่ได้มา
print(X[:10]) # เนื่องจากเยอะขอแสดงแค่ ๑๐ ตัวแรกพอ
print(z[:100]) # แสดงแค่ ๑๐๐ ตัวแรก
print(z[:100]) # แสดงแค่ ๑๐๐ ตัวแรก
ได้
[[ -0.47833185 -1.03782344]
[ 1.55130783 0.50396236]
[ -8.41234362 1.25698346]
[ -9.16511718 1.63663075]
[ 3.70073197 -4.55646884]
[ -2.55585116 8.89175305]
[ 2.31022323 0.50023084]
[ -2.03417759 10.26677945]
[ -7.50242695 0.31749443]
[-10.68328818 2.48912317]]
[0 0 3 3 2 1 0 1 3 3 3 1 0 0 1 4 4 2 1 4 4 0 0 4 3 0 2 0 0 2 4 0 3 2 3 1 4
3 3 1 0 3 0 0 0 4 1 1 4 1 0 1 0 0 0 4 0 4 0 0 3 3 1 0 3 2 3 3 0 4 0 2 0 2
2 0 2 0 2 0 0 4 3 0 1 2 2 3 3 3 2 1 1 1 3 4 4 1 2 0]
[ 1.55130783 0.50396236]
[ -8.41234362 1.25698346]
[ -9.16511718 1.63663075]
[ 3.70073197 -4.55646884]
[ -2.55585116 8.89175305]
[ 2.31022323 0.50023084]
[ -2.03417759 10.26677945]
[ -7.50242695 0.31749443]
[-10.68328818 2.48912317]]
[0 0 3 3 2 1 0 1 3 3 3 1 0 0 1 4 4 2 1 4 4 0 0 4 3 0 2 0 0 2 4 0 3 2 3 1 4
3 3 1 0 3 0 0 0 4 1 1 4 1 0 1 0 0 0 4 0 4 0 0 3 3 1 0 3 2 3 3 0 4 0 2 0 2
2 0 2 0 2 0 0 4 3 0 1 2 2 3 3 3 2 1 1 1 3 4 4 1 2 0]
หมายเลขใน z จะสัมพันธ์กับตำแหน่งที่ระบุใน X โดยหมายเลขเดียวกันจะมีค่า X ใกล้เคียงกัน
ลองนำมาวาดแผนภาพการกระจายเพื่อดูว่าค่าของแต่ละกลุ่มเป็นอย่างไรบ้าง
import matplotlib.pyplot as plt
plt.figure(figsize=[6,6])
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k')
plt.show()
plt.figure(figsize=[6,6])
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k')
plt.show()

จะได้แบบนี้คือเป็นกลุ่มก้อน ๕ กลุ่ม ภาพที่ได้อาจต่างกันออกไปขึ้นอยู่กับว่าสุ่มได้แบบไหน ลองทำซ้ำดูหลายๆครั้งได้จะเห็นภาพและเข้าใจฟังก์ชันนี้มากขึ้น
ถ้าลองเปลี่ยน n_features เป็น 3 ก็จะได้ข้อมูลเป็นสามมิติ
ลองสร้างข้อมูลสามมิติซึ่งแบ่งเป็น ๗ กลุ่มจากนั้นก็วาดแผนภาพการกระจายในสามมิติด้วย mpl_toolkits.mplot3d
from mpl_toolkits.mplot3d import Axes3D
X,z = datasets.make_blobs(n_samples=1000,n_features=3,centers=7)
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[X.min(),X.max()],ylim=[X.min(),X.max()])
ax.scatter(X[:,0],X[:,1],X[:,2],c=z,edgecolor='k',cmap='rainbow')
plt.show()
X,z = datasets.make_blobs(n_samples=1000,n_features=3,centers=7)
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[X.min(),X.max()],ylim=[X.min(),X.max()])
ax.scatter(X[:,0],X[:,1],X[:,2],c=z,edgecolor='k',cmap='rainbow')
plt.show()

***เรื่องของการใช้ mpl_toolkits.mplot3d เพื่อวาดภาพสามมิตินี้ยังไม่เคยเขียนลงบล็อกนี้แต่ขอนำมาใช้ก่อน ไว้มีโอกาสจะเขียนถึงเพราะเป็นเรื่องที่สำคัญต้องใช้งานเยอะอยู่
จะเพิ่ม n_features เป็นกี่มิติก็ได้ แต่ถ้า 4 ขึ้นไปคงจะไม่สามารถวาดแผนภาพการกระจายแสดงให้เห็นได้แล้ว เข้าสู่โลกที่สามัญสำนึกของมนุษย์ยากจะจินตนาการถึง แต่ถึงอย่างนั้นข้อมูลทั่วไปก็มักจะมีหลายมิติ จะไม่พูดถึงคงไม่ได้ เพียงแต่จะไม่สามารถวาดแผนภาพง่ายๆให้ดูได้
นอกจากนี้สามารถปรับอะไรได้อีกหลายอย่าง สรุปพารามิเตอร์ที่ใส่ได้มีดังนี้
| ความหมาย | ค่าตั้งต้น | |
|---|---|---|
| n_samples | จำนวนข้อมูลทั้งหมด | 100 |
| n_features | จำนวนตัวแปรต้น | 2 |
| centers | จำนวนกลุ่มก้อน | 3 |
| cluster_std | ส่วนเบี่ยงเบนมาตรฐานของการกระจาย | 1.0 |
| center_box | ขอบเขตที่จะสุ่มจุดศูนย์กลางการกระจาย | (-10.0,10.0) |
| shuffle | จะสุ่มการจัดเรียงแต่ละกลุ่มหรือไม่ | True |
| random_state | หมายเลขชุดของการสุ่ม | None |
ถ้าต้องการให้ข้อมูลมีการกระจายมากขึ้นก็อาจปรับค่า cluster_std ให้สูงขึ้น แต่ถ้ามากไปแต่ละกลุ่มก็จะปนๆกันได้ง่าย
หรือถ้าลด center_box ให้ขอบเขตการสุ่มใจกลางแต่ละกลุ่มแคบลงก็จะเกิดการปนกันได้ง่ายเช่นกัน
ข้อมูลที่มีการปนกันแยกออกยากในบางส่วนก็อาจใช้เป็นตัวอย่างการเรียนรู้ในกรณีที่มีความไม่แน่นอนของข้อมูลสูงได้ ขึ้นอยู่กับการใช้งาน
ส่วน random_state นั้นคล้ายกับ np.random.seed ของ numpy คือเอาไว้ใช้เมื่อต้องการให้สุ่มได้ข้อมูลชุดเดิมๆ เช่นถ้าใส่ random_state=100 แล้วลองรันซ้ำๆดูไม่ว่ากี่ครั้งก็จะได้เท่าเดิม แต่ถ้าลองเปลี่ยนเป็น random_state=101 จะได้ค่าที่ต่างไปอีกค่า แต่ถ้าไม่ใส่อะไรจะเท่ากับเป็น Nonoe ก็จะสุ่มได้ข้อมูลต่างกันไปตลอดหมดทุกครั้ง
ตอนนี้ได้รู้วิธีสร้างข้อมูลทดสอบขึ้นมาแล้ว ต่อไปลองนำมาใช้เป็นตัวอย่างการทดสอบการวิเคราะห์การถดถอยโลจิสติก
เพียงแต่ว่าตอนนี้แบบจำลองที่ได้ทำขึ้นนั้นใช้ได้แค่สำหรับการแบ่งกลุ่มเป็นสองกลุ่ม ดังนั้นใช้ centers=2 ซึ่งจะได้ z เป็นเลข 0 หรือ 1 สำหรับแบบจำลองการวิเคราะห์การถดถอยโลจิสติกแบบที่แบ่งข้อมูลเป็นหลายกลุ่มนั้นจะพูดถึงในโอกาสต่อไป
ในที่นี้จะใช้แบบจำลองวิเคราะห์การถดถอยโลจิสติกที่มีการปรับมาตรฐานที่เขียนถึงไว้ใน https://phyblas.hinaboshi.com/20161124
เพื่อเป็นการประหยัดพื้นที่ จะไม่เขียนส่วนนิยามคลาสในหน้านี้ซ้ำ ให้นำส่วนที่นิยามฟังก์ชัน sigmoid กับคลาส ThotthoiLogistic จากในหน้านั้นมาใช้
มีสรุปลงเอาไว้ใน github คัดลอกจากในนี้มาได้ https://github.com/phyblas/rianrupython/blob/master/kanrianrukhongkhrueang/thotthoi_logistic_2.py
จากนั้นจึงต่อด้วยโค้ดต่อไปนี้ ลองเริ่มจากแบบสองมิติซึ่งสามารถเห็นภาพได้ง่ายกันก่อน
X,z = datasets.make_blobs(n_samples=1000,n_features=2,centers=2,cluster_std=2,random_state=7)
eta = 0.00002 # อัตราการเรียนรู้
n_thamsam = 5000 # จำนวนครั้งที่ทำซ้ำ
tl = ThotthoiLogistic(eta)
tl.rianru(X,z,n_thamsam)
x_sen = np.array([X[:,0].min(),X[:,0].max()])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(X)==z
plt.axes(aspect=1,xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.plot(x_sen,y_sen,lw=3,zorder=0)
plt.scatter(X[thukmai==1,0],X[thukmai==1,1],c=z[thukmai==1],s=50,edgecolor='k',cmap='spring')
plt.scatter(X[thukmai==0,0],X[thukmai==0,1],c=z[thukmai==0],s=50,edgecolor='r',lw=2,cmap='spring')
plt.figure(figsize=[9,4])
plt.subplot(211)
plt.title(u'ผลรวมความคลาดเคลื่อนกำลังสอง',fontname='Tahoma')
plt.plot(tl.sse)
plt.tick_params(labelbottom='off')
plt.subplot(212)
plt.title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
plt.show()
eta = 0.00002 # อัตราการเรียนรู้
n_thamsam = 5000 # จำนวนครั้งที่ทำซ้ำ
tl = ThotthoiLogistic(eta)
tl.rianru(X,z,n_thamsam)
x_sen = np.array([X[:,0].min(),X[:,0].max()])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(X)==z
plt.axes(aspect=1,xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.plot(x_sen,y_sen,lw=3,zorder=0)
plt.scatter(X[thukmai==1,0],X[thukmai==1,1],c=z[thukmai==1],s=50,edgecolor='k',cmap='spring')
plt.scatter(X[thukmai==0,0],X[thukmai==0,1],c=z[thukmai==0],s=50,edgecolor='r',lw=2,cmap='spring')
plt.figure(figsize=[9,4])
plt.subplot(211)
plt.title(u'ผลรวมความคลาดเคลื่อนกำลังสอง',fontname='Tahoma')
plt.plot(tl.sse)
plt.tick_params(labelbottom='off')
plt.subplot(212)
plt.title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
plt.show()


ถ้ากลุ่มก้อนมีการซ้อนทับกันแบบที่เห็นนี้ไม่ว่าจะเรียนรู้กี่ครั้งก็ไม่มีทางทายได้ถูกทั้งหมด แต่ถึงอย่างนั้นการเรียนรู้ก็ไปในทิศทางที่ทำให้จำนวนที่ทายถูกมีมากที่สุดเท่าที่จะทำได้
กรณีปัญหาแบบนี้เราอาจทำได้แค่หาความน่าจะเป็นที่จะอยู่กลุ่มนั้นๆเท่านั้น
เดิมทีตอนที่เราหาว่าเป็นกลุ่ม 0 หรือ 1 เราทำการคำนวณความน่าจะเป็นด้วยฟังก์ชันซิกมอยด์ด้วยเมธอด ha_sigmoid จากนั้นเมธอด thamnai ก็นำค่าไปใช้โดยดูว่าถ้าสูงกว่า 0.5 ก็ตัดเป็น 1 ถ้าต่ำกว่าก็ตัดเป็น 0
ดังนั้นแทนที่เราจะเอาค่าจากเมธอด thamnai ถ้าคำนวณค่าจากเมธอด ha_sigmoid ก็จะได้ค่าความน่าจะเป็นที่จะอยู่ในกลุ่ม 1
ลองวาดแผนภาพไล่สีแสดงความน่าจะเป็นดู
xm,ym = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),100),np.linspace(X[:,1].min(),X[:,1].max(),100))
Xm = np.stack([xm.ravel(),ym.ravel()],1)
zm = tl.ha_sigmoid(Xm).reshape(100,100)
plt.axes(xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.pcolormesh(xm,ym,zm,cmap='spring',alpha=0.3)
plt.colorbar(pad=0.02)
plt.scatter(X[:,0],X[:,1],c=z,s=50,edgecolor='k',lw=2,cmap='spring')
plt.show()
Xm = np.stack([xm.ravel(),ym.ravel()],1)
zm = tl.ha_sigmoid(Xm).reshape(100,100)
plt.axes(xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.pcolormesh(xm,ym,zm,cmap='spring',alpha=0.3)
plt.colorbar(pad=0.02)
plt.scatter(X[:,0],X[:,1],c=z,s=50,edgecolor='k',lw=2,cmap='spring')
plt.show()

ต่อมาคราวนี้ลองใช้กับข้อมูลสามมิติดูบ้าง
X,z = datasets.make_blobs(n_samples=1000,n_features=3,centers=2,cluster_std=2,random_state=7)
eta = 0.0001
n_thamsam = 100
tl = ThotthoiLogistic(eta)
tl.rianru(X,z,n_thamsam)
xm = np.linspace(X.min(),X.max(),6)
ym = np.linspace(X.min(),X.max(),6)
xm,ym = np.meshgrid(xm,ym)
zm = -(tl.w[0]+tl.w[1]*xm+tl.w[2]*ym)/tl.w[3]
thukmai = tl.thamnai(X)==z
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d')
ax.plot_surface(xm,ym,zm,rstride=1,cstride=1,zorder=0,alpha=0.2)
ax.scatter(X[thukmai==1,0],X[thukmai==1,1],X[thukmai==1,2],c=z[thukmai==1],sizes=z[thukmai==1]+24,edgecolor='k',cmap='spring')
ax.scatter(X[thukmai==0,0],X[thukmai==0,1],X[thukmai==0,2],c=z[thukmai==0],sizes=z[thukmai==1]+25,edgecolor='r',lw=2,cmap='spring')
plt.show()
eta = 0.0001
n_thamsam = 100
tl = ThotthoiLogistic(eta)
tl.rianru(X,z,n_thamsam)
xm = np.linspace(X.min(),X.max(),6)
ym = np.linspace(X.min(),X.max(),6)
xm,ym = np.meshgrid(xm,ym)
zm = -(tl.w[0]+tl.w[1]*xm+tl.w[2]*ym)/tl.w[3]
thukmai = tl.thamnai(X)==z
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d')
ax.plot_surface(xm,ym,zm,rstride=1,cstride=1,zorder=0,alpha=0.2)
ax.scatter(X[thukmai==1,0],X[thukmai==1,1],X[thukmai==1,2],c=z[thukmai==1],sizes=z[thukmai==1]+24,edgecolor='k',cmap='spring')
ax.scatter(X[thukmai==0,0],X[thukmai==0,1],X[thukmai==0,2],c=z[thukmai==0],sizes=z[thukmai==1]+25,edgecolor='r',lw=2,cmap='spring')
plt.show()
กรณีสามมิตินั้นแทนที่จะใช้แค่เส้นเป็นตัวคั่นก็ต้องเปลี่ยนเป็นใช้ระนาบในการคั่นแทน

สุดท้ายลองกับห้ามิติดู คราวนี้มิติมากกว่าสามจึงทำเป็นภาพไม่ได้ ได้แค่ดูผลว่าค่าความคลาดเคลื่อนลดลงและจำนวนที่ถูกมากขึ้นเท่านั้น
X,z = datasets.make_blobs(n_samples=10000,n_features=5,centers=2,cluster_std=4,random_state=7)
eta = 0.00001
n_thamsam = 2500
tl = ThotthoiLogistic(eta)
tl.rianru(X,z,n_thamsam)
plt.figure(figsize=[10,4])
plt.subplot(211)
plt.title(u'ผลรวมความคลาดเคลื่อนกำลังสอง',fontname='Tahoma')
plt.plot(tl.sse)
plt.tick_params(labelbottom='off')
plt.subplot(212)
plt.title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
plt.show()
eta = 0.00001
n_thamsam = 2500
tl = ThotthoiLogistic(eta)
tl.rianru(X,z,n_thamsam)
plt.figure(figsize=[10,4])
plt.subplot(211)
plt.title(u'ผลรวมความคลาดเคลื่อนกำลังสอง',fontname='Tahoma')
plt.plot(tl.sse)
plt.tick_params(labelbottom='off')
plt.subplot(212)
plt.title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
plt.show()

อาจลองเปลี่ยนค่าต่างๆแล้วทดสอบแต่ละกรณีดูไปเรื่อยๆ
เท่านี้ก็จะเห็นได้ว่าแบบจำลองการวิเคราะห์การถดถอยโลจิสติกที่สร้างขึ้นนั้นสามารถใช้ได้ในข้อมูลที่มีตัวแปรต้นกี่ตัวก็ได้
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib