numpy & matplotlib เบื้องต้น บทที่ ๑๙: ดัชนีบูลและดัชนีแฟนซี กับการคัดกรองส่วนประกอบในอาเรย์
เขียนเมื่อ 2016/06/11 23:53
แก้ไขล่าสุด 2022/07/21 20:30
ในบทที่ ๒ ได้พูดถึงการเข้าถึงสมาชิกในอาเรย์ในเบื้องต้นไปแล้ว แต่นั่นเป็นแค่เบื้องต้น มีวิธีการเข้าถึงอาเรย์ที่ยืดหยุ่นกว่านั้นแม้ว่าอาจจะเข้าใจยากสักหน่อย นั่นคือการอ้างอิงเข้าถึงส่วนประกอบบางส่วนภายในอาเรย์โดยใช้อาเรย์อีกอันมาทำหน้าที่เป็นดัชนี
อาเรย์ที่ใช้เป็นดัชนีได้นั้นต้องเป็นอาเรย์ของจำนวนเต็ม หรือไม่ก็อาเรย์ของข้อมูลชนิดบูล (True และ False)
กรณีที่ใช้อาเรย์เป็นข้อมูลชนิดบูลจะเป็นการเข้าถึงสมาชิกภายในอาเรย์เฉพาะที่ค่าในอาเรย์ของดัชนีนั้นเป็น True
กรณีที่ใช้อาเรย์เป็นจำนวนเต็ม จำนวนเต็มนั้นจะแทนเลขดัชนีของข้อมูลที่ต้องการ ซึ่งเมื่อประกอบด้วยหลายตัวก็ทำให้เราเข้าถึงสมาชิกในตำแหน่งที่ต้องการทีละหลายตัวตามที่ระบุได้ การใช้ดัชนีในลักษณะนี้บางครั้งถูกเรียกว่าดัชนีแฟนซี (fancy index)
ทั้งดัชนีบูลและดัชนีแฟนซีเป็นเครื่องมือที่สะดวกมากในการคัดกรองส่วนประกอบภายในอาเรย์ออกมาบางส่วนตามที่เราต้องการโดยการกำหนดเงื่อนไขบางอย่าง
นอกจากนี้ในนี้จะพูดถึงฟังก์ชันส่วนหนึ่งที่เกี่ยวข้อง ซึ่งก็ใช้ในการคัดกรองและจัดการกับสมาชิกในอาเรย์ ได้แก่ np.where, np.select และ np.choose
การใช้อาเรย์ของบูลเป็นดัชนีในอาเรย์
สมมุติมีอาเรย์หนึ่งมิติอยู่ตัวหนึ่ง
การเข้าถึงสมาชิกภายในอาเรย์ทีละหลายตัวนั้นก็ทำได้แบบเดียวกับลิสต์ แต่นอกจากนี้แล้วยังสามารถใช้อาเรย์ที่เก็บออบเจ็กต์ชนิดบูล
การเขียนแบบนี้อาจดูยุ่งยากยืดยาวกว่าเดิม แต่ความจริงแล้วมีประโยชน์ในทางประยุกต์ใช้มาก นั่นเพราะปกติหากเราเอาอาเรย์มาใช้ในนิพจน์การเปรียบเทียบก็จะคืนค่าออกมา เป็นอาเรย์ของข้อมูลชนิดบูล
ดังนั้นหากนำผลที่ได้จากนิพจน์นี้ไปใช้เป็นดัชนีในการเข้าถึงสมาชิกในอาเรย์ละก็ จะได้อาเรย์ที่มีสมาชิกเหลือแค่ตัวที่เข้าเงื่อนไข
ผลที่ได้ก็คือเป็นการคัดกรองสมาชิกภายในอาเรย์ให้เหลือเฉพาะบางส่วน การเขียนแบบนี้จึงมีประโยชน์มาก หากประยุกต์ให้ดีจะสามารถสร้างอาเรย์ในแบบที่ต้องการได้ง่ายมาก
ตัวอย่างการประยุกต์ใช้ เช่นลองคัดกรองข้อมูลบางส่วนที่เข้าเงื่อนไข แบ่งเอาไว้เป็นส่วนหนึ่ง ส่วนที่ไม่เข้าเงื่อนไขก็ไว้อีกส่วนหนึ่ง
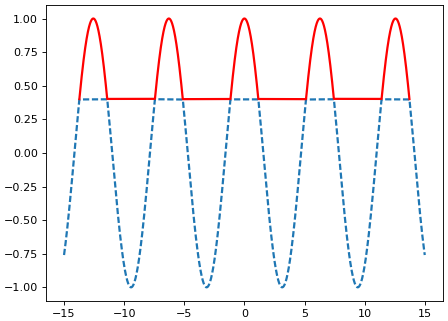
เช่นลองแบ่งกราฟ sin ออกเป็น ๒ ส่วน ส่วนที่ค่าสูงกว่าและต่ำกว่า 0.4
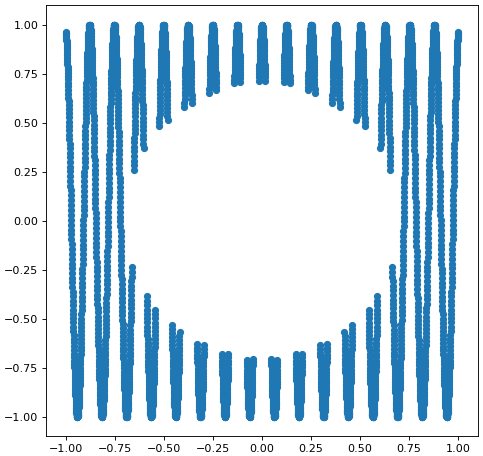
หรืออาจใช้เงื่อนไขเป็นทั้งแกน x และ y ร่วมกัน เช่นคัดกรองจุดที่อยู่ภายในรัศมี 0.7 จากใจกลางออกไป
เราสามารถใช้วิธีนี้เข้าถึงสมาชิกบางส่วนเพื่อไปแก้ไขบางส่วน
เช่น แก้ข้อมูลที่ติดลบให้เป็น 0 ให้หมด
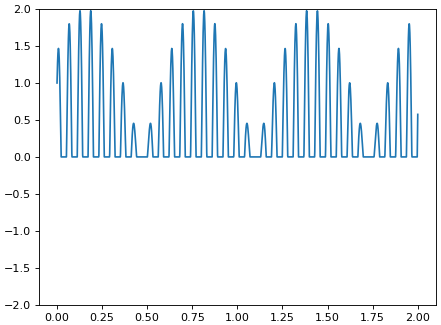
ลองดูตัวอย่างโดยวาดกราฟซึ่งมีการตัดข้อมูลส่วนที่ต่ำกว่า 0 ให้กลายเป็น 0 ทั้งหมด
หากใช้ตัวแปรมารับอาเรย์ที่ได้จากการเข้าถึงด้วยดัชนีบูล จะมีการคัดลอกค่าทั้งหมดเข้าไปเก็บในตัวแปรนั้น ไม่ได้เกิดการถ่ายทอด กล่าวคือหากมีการเปลี่ยนแปลงค่าภายในตัวแปรใหม่นั้นจะไม่กระทบถึงข้อมูลภายในอาเรย์เดิม
ซึ่งจะเห็นว่าต่างจากการใช้ดัชนีเป็นเลขธรรมดาซึ่งมีคุณสมบัติการถ่ายทอด ดังนั้นต้องระวังอย่าสับสนกัน
ดัชนีในสองมิติ
กรณีที่ใช้ในสองมิติขึ้นไปจะมีความซับซ้อนขึ้นมาแต่หากเข้าใจแล้วก็จะประยุกต์ใช้ได้ดี
ก่อนอื่นทวนเนื้อหาจากบทที่แล้วสักหน่อย อาเรย์สองมิติประกอบไปด้วยแถว (แนวตั้ง) กับหลัก (แนวนอน)
ขอใช้อาเรย์นี้เป็นตัวอย่าง
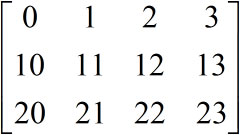
การเข้าถึงสมาชิกในอาเรย์สามารถใช้ลิสต์ของดัชนี โดยใช้เป็น [แถว,หลัก]
ถ้าใส่แทนเลขหลักด้วย : หรือไม่ใส่เลย จะเป็นการเลือกเอาสมาชิกจากทุกหลักในแถวนั้น
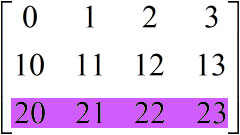
แต่ถ้าใส่แทนเลขหลักด้วย : หรือไม่ใส่เลย และใส่แทนเลขแถวด้วยลิสต์ จะเป็นการเลือกเอาหลักที่มีดัชนีเป็นทุกตัวในลิสต์นั้น
ถ้าใส่แทนเลขแถวด้วย : ใส่แทนหลักด้วยตัวเลขจะกลายเป็นการเลือกเอาสมาชิกจากทุกแถวในหลักนั้น
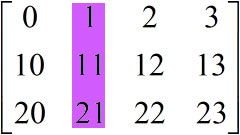
แต่ถ้าใส่แทนเลขแถวด้วย : แทนหลักด้วยลิสต์ ผลที่จะเป็นการเลือกเอาแถวที่มีดัชนีเป็นทุกตัวในลิสต์นั้นมาพร้อมกัน

จากตรงนี้ เราลองเปลี่ยนมาลองใช้อาเรย์ชนิดบูลในการเข้าถึงสมาชิกในอาเรย์เช่นเดียวกับที่ทำในหนึ่งมิติ
ลองสร้างอาเรย์ที่เก็บค่าความจริงเท็จขึ้นมา จากนั้นลองนำไปใช้เป็นตัวระบุดัชนีในอาเรย์ z

ซึ่งมีค่าเท่ากับ z[2] หรือ z[2,:]
จะเห็นว่าอาเรย์ fft ในที่นี้เป็นตัวระบุว่าจะเอาสมาชิกในแถวไหนของ z
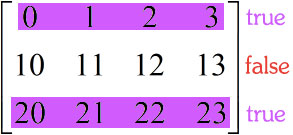
ถ้าหากมี True อยู่ ๒ ตัว ก็จะได้ออกมา ๒ แถว
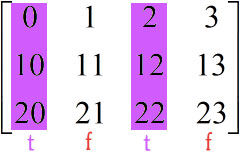
ซึ่งมีค่าเท่ากับ z[[1,2]] หรือ z[[1,2],:]
หากใช้วิธีเดียวกันแทนเลขหลักก็ได้ผลในลักษณะเดียวกัน
ทีนี้อาเรย์มีคุณสมบัติการกระจาย ถ้าหากเอาอาเรย์มาเทียบกับค่าอะไรบางอย่างก็สามารถได้ผลออกมาเป็นอาเรย์ของค่าความจริงเท็จ
จะเห็นว่าในนี้มีแค่สมาชิกตัวเดียวที่มีค่าเป็น 21 จึงคืนค่าเป็น True ที่เหลือเป็น False
ถ้าใช้วิธีนี้กับบางส่วนของอาเรย์ก็จะได้อาเรย์ของค่าความจริงเท็จที่มีมิติเดียว
ซึ่งเป็นสิ่งที่สามารถถูกนำมาใช้เป็นค่าดัชนีได้
ดังนั้นหากนำมาประยุกต์เราจะสามารถใช้เพื่อคัดกรองสมาชิกได้
หากนำทั้งอาเรย์มาเข้านิพจน์หาค่าความจริงเท็จก็จะได้อาเรย์ของ True False ที่มีขนาดตามนั้น เช่น
ซึ่งเมื่อเราเอาอาเรย์ที่ได้ตัวนี้มาเป็นดัชนีให้กับตัวอาเรย์นั้นเอง ผลที่ได้จะออกมาในรูปของอาเรย์หนึ่งมิติซึ่งประกอบด้วยสมาชิกเฉพาะส่วนที่เป็น True
ซึ่งจะเห็นว่าแบบนี้ทำให้สูญเสียมิติไป อย่างไรก็ตามแม้จะอยู่ในรูปหนึ่งมิติแต่อาเรย์ตัวนี้ก็ชี้ถึงสมาชิกแต่ละตัวในอาเรย์ตัวเดิมนี้อยู่ เราสามารถทำการแก้ข้อมูลมันได้
เท่านี้ตัวเลขที่มีค่ามากกว่า 50 ก็ถูกเปลี่ยนให้กลายเป็น 0 หมด
การใช้อาเรย์ของจำนวนเต็มเป็นดัชนี
อาเรย์ของข้อมูลชนิดจำนวนเต็ม รวมทั้งลิสต์ของจำนวนเต็ม สามารถใช้เพื่อเป็นดัชนีเพื่ออ้างอิงถึงสมาชิกในอาเรย์ได้ โดยจะเป็นการเข้าถึงสมาชิกทีละหลายตัวตามตัวเลขที่ระบุไว้นั้น
ตัวอย่าง
การใช้ในลักษณะนี้มีประโยชน์มาก สามารถเอาไปประยุกต์ใช้เช่นเวลาที่มีข้อมูลที่ยาวมากๆแล้วต้องการจะยกแต่บางส่วนออกมาเป็นช่วงๆ
เช่น เวลาที่ต้องการวาดแค่บางจุดบนกราฟ
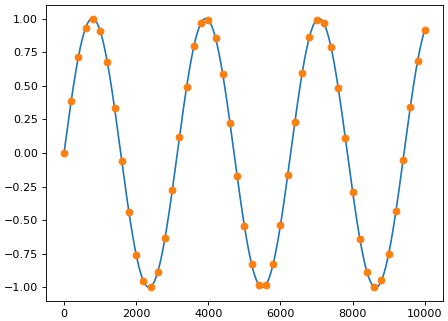
จะเห็นว่ามีข้อมูล 10001 ตัวที่ประกอบกันเป็นกราฟ sin แต่เราต้องการนำข้อมูลแค่บางส่วน โดยในที่นี้ให้วาดจุดแค่ทุก 200 ค่า กรณีแบบนี้ดัชนีแฟนซีจะมีประโยชน์มาก
กรณีที่มีการนำตัวแปรมารับค่าอาเรย์ที่ได้จากดัชนีแฟนซีก็จะได้ผลเช่นเดียวกับดัชนีบูลก็คือเป็นการคัดลอกอาเรย์ไปเก็บไว้ในตัวแปรใหม่ ไม่ใช่การถ่ายทอด หากมีการแก้ไขค่าอะไรในตัวแปรใหม่ก็จะไม่กระทบถึงอาเรย์ตัวเดิม
เรื่องของดัชนีแฟนซีนี้อาจจะเข้าใจยาก แต่หากใช้จนคล่องแล้วมันจะเป็นวิธีการในการคัดกรององค์ประกอบที่ทรงพลังมาก ยังไงก็คงจะพยายามเข้าใจมันสักหน่อย
np.where
เราสามารถใช้ฟังก์ชัน np.where เพื่อหาค่าดัชนีของสมาชิกภายในอาเรย์ที่เข้ากับเงื่อนไขบางอย่างที่ต้องการได้
np.where ต้องการอาร์กิวเมนต์เป็นนิพจน์ของอาเรย์ซึ่งให้ค่าความจริงเท็จ เช่น x>10 x==20 x!=3 เป็นต้น จากนั้นจะคืนค่าออกมาเป็นดัชนีของอาเรย์นั้นที่เข้าเงื่อนไข (ให้ผลค่าความจริงเป็นจริง)
ตัวอย่าง
จะเห็นว่า np.where(a>11) จะได้ผลออกมาเป็นอาเรย์ที่ประกอบไปด้วยเลขดัชนีของสมาชิกใน a ที่ให้ a>11 เป็น True
จากนั้นหากเอาผลที่ได้จาก np.where นี้มาใช้เป็นดัชนี
จะเห็นว่าผลที่ได้จะเหมือนกับ a[a>11]
ซึ่งถ้าหากนำมาใช้ในลักษณะนี้ก็อาจดูไม่จำเป็น เพราะทำให้เขียนยาวขึ้นแต่ผลเหมือนเดิม
นอกจากนี้แล้ว np.where มีวิธีการใช้งานที่มากกว่านั้น ซึ่งทำได้โดยใส่อาร์กิวเมนต์เพิ่มเป็นสามตัว แบบนั้นจะเป็นการนำอาเรย์ตัวเดิมมาจัดการอะไรบางอย่างโดยขึ้นกับเงื่อนไขที่ ใส่ลงไป
การทำงานอาจเข้าใจยากเล็กน้อย ลองดูตัวอย่างเพื่อให้พอเห็นภาพ
จะเห็นว่าการทำงานของ np.where ในที่นี้ก็คือจะพิจารณาค่าความจริงเท็จจากอาร์กิวเมนต์ตัวที่หนึ่ง ถ้าหากว่าเป็นจริงก็จะคืนค่าออกมาตามค่าที่ใส่ไว้ในอาร์กิวเมนต์ตัวที่สอง ถ้าเป็นเท็จก็จะคืนค่าตามอาร์กิวเมนต์ตัวที่สาม
ในที่นี้จะเห็นว่า สมาชิก ๒ ตัวแรกคือ 10. กับ 10.6 ไม่เข้าเงื่อนไข (ให้ค่า False) จึงได้รับค่าที่อยู่ในอาร์กิวเมนต์ตัวที่สาม ก็คือ 2 ส่วนที่เหลือเป็น True จึงได้ค่า 1
ค่าที่ใส่นั้นอาจไม่ใช่แค่จำนวนค่าคงที่เท่านั้นแต่สามารถใส่ตัวอาเรย์ตัวนั้นเพื่อให้มันนำเอาสมาชิกในลำดับที่ตรงกันมาคำนวณ
เช่น
ในที่นี้สมาชิกใน a สองตัวแรกไม่เข้าเงื่อนไข a>11 จึงได้ค่าเป็น a-10 ค่าจึงลดลงไป 10 ส่วนตัวที่เหลือเข้าเงื่อนไขจึงบวกไป 10
อาเรย์ที่ใช้เป็นเงื่อนไขในอาร์กิวเมนต์ตัวแรกกับอาเรย์ที่ใช้พิจารณาค่าอาจไม่ใช่ตัวเดียวกันก็ได้ ขอแค่มีสมาชิกจำนวนเท่ากัน
ตัวอย่าง
ในตัวอย่างนี้ใช้ c เป็นเงื่อนไขโดยจะเห็นว่าตัวที่ 0,2,4 เป็น False ส่วน b ถูกใช้เป็นอาเรย์สำหรับนำค่ามาคำนวณ ค่าที่ได้จาก np.where ในที่นี้จะเป็นค่าของสมาชิกใน b ในตำแหน่งที่ได้ True ส่วนตำแหน่งที่ได้ False จะถูกหาร 5
และในบางครั้งอาจใช้เพื่อคัดเลือกว่าจะเอาค่าจากอาเรย์ตัวไหนตามเงื่อนไขที่กำหนดก็ได้
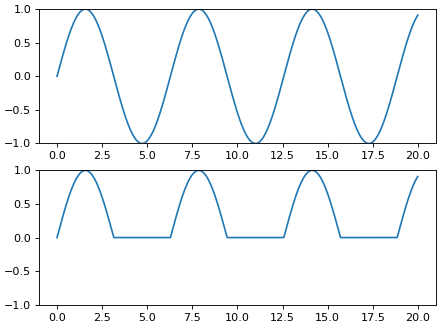
เราอาจนำมาใช้เพื่อกรองค่าในฟังก์ชันบางส่วนที่ไม่ตรงเงื่อนไขที่ต้องการ ตัวอย่างเช่นลองสร้างกราฟของฟังก์ชัน sin โดยที่ให้ค่าที่ต่ำกว่า 0 เป็น 0 ไปให้หมด
np.select
มีอีกฟังก์ชันซึ่งคล้ายๆกับ np.where สามารถทำให้ได้ผลที่เหมือนกันได้ นั่นคือ np.select
ฟังก์ชันนี้จะทำการสร้างอาเรย์ใหม่ขึ้นมาจากอาเรย์เดิมที่ใช้เป็นตัวกำหนดเงื่อนไข ซึ่งจะใส่เป็นอาร์กิวเมนต์ตัวแรก ค่าในอาเรย์ที่สร้างขึ้นใหม่จะกำหนดโดยอาร์กิวเมนต์ตัวหลัง
ในตัวอย่างนี้สมาชิกใน x สองตัวแรก 1.1,1.3 นั้นน้อยว่า 1.5 จึงเข้าเงื่อนไขหลังจึง
เงื่อนไขแรกกับเงื่อนไขหลังไม่จำเป็นต้องครอบคลุมทุกสิ่งที่เป็นไปได้ หากมีสมาชิกไหนที่ไม่เข้ากับเงื่อนไขเลยก็จะได้ค่า 0 เช่น
เงื่อนไขอาจมีกี่ตัวก็ได้ ซึ่งก็จะต้องเตรียมค่าที่จะใช้เมื่อเข้าเงื่อนไขนั้นให้มีจำนวนเท่ากันด้วย
ค่าในลิสต์ตัวหลังก็อาจใช้เป็นอาเรย์ตัวที่พิจารณาเองได้
และก็อาจใช้เป็นอาเรย์ตัวอื่นที่มีขนาดเท่ากัน
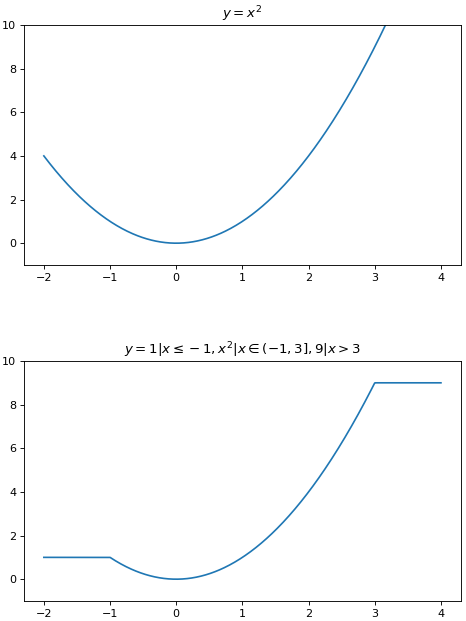
เราอาจประยุกต์ใช้เพื่อทำกราฟที่มีค่าแบ่งเป็นช่วงๆก็ได้
np.choose
ฟังก์ชัน np.choose มีไว้สร้างอาเรย์ขึ้นจากรายการ (ลิสต์หรืออาเรย์) ของเลขดัชนี และรายการของค่าที่ต้องการนำมาใช้
เพื่อให้เข้าใจจำเป็นต้องดูตัวอย่างการใช้
จากตัวอย่างนี้จะเป็นการสร้างอาเรย์ที่ใช้อาร์กิวเมนต์ตัวแรกเป็นเลขดัชนีและ ตัวหลังเป็นค่าที่จะให้นำมาใช้เมื่อถูกอ้างอิงจากดัชนี ผลลัพธ์ที่ได้จะมีจำนวนสมาชิกเท่ากับอาเรย์ที่เก็บดัชนีตัวเลือก
จริงๆแล้วเราสามารถได้ผลแบบเดียวกันนี้ด้วยการเขียนง่ายๆเป็น g[s]
ซึ่งก็เป็นไปตามหลักของดัชนีแฟนซี
อ้างอิง
อาเรย์ที่ใช้เป็นดัชนีได้นั้นต้องเป็นอาเรย์ของจำนวนเต็ม หรือไม่ก็อาเรย์ของข้อมูลชนิดบูล (True และ False)
กรณีที่ใช้อาเรย์เป็นข้อมูลชนิดบูลจะเป็นการเข้าถึงสมาชิกภายในอาเรย์เฉพาะที่ค่าในอาเรย์ของดัชนีนั้นเป็น True
กรณีที่ใช้อาเรย์เป็นจำนวนเต็ม จำนวนเต็มนั้นจะแทนเลขดัชนีของข้อมูลที่ต้องการ ซึ่งเมื่อประกอบด้วยหลายตัวก็ทำให้เราเข้าถึงสมาชิกในตำแหน่งที่ต้องการทีละหลายตัวตามที่ระบุได้ การใช้ดัชนีในลักษณะนี้บางครั้งถูกเรียกว่าดัชนีแฟนซี (fancy index)
ทั้งดัชนีบูลและดัชนีแฟนซีเป็นเครื่องมือที่สะดวกมากในการคัดกรองส่วนประกอบภายในอาเรย์ออกมาบางส่วนตามที่เราต้องการโดยการกำหนดเงื่อนไขบางอย่าง
นอกจากนี้ในนี้จะพูดถึงฟังก์ชันส่วนหนึ่งที่เกี่ยวข้อง ซึ่งก็ใช้ในการคัดกรองและจัดการกับสมาชิกในอาเรย์ ได้แก่ np.where, np.select และ np.choose
การใช้อาเรย์ของบูลเป็นดัชนีในอาเรย์
สมมุติมีอาเรย์หนึ่งมิติอยู่ตัวหนึ่ง
import numpy as np
z = np.array([0,1,2,3,4,5])
z = np.array([0,1,2,3,4,5])
การเข้าถึงสมาชิกภายในอาเรย์ทีละหลายตัวนั้นก็ทำได้แบบเดียวกับลิสต์ แต่นอกจากนี้แล้วยังสามารถใช้อาเรย์ที่เก็บออบเจ็กต์ชนิดบูล
z[np.array([False, False, True, False, True, False])] # ได้ [2 4]
การเขียนแบบนี้อาจดูยุ่งยากยืดยาวกว่าเดิม แต่ความจริงแล้วมีประโยชน์ในทางประยุกต์ใช้มาก นั่นเพราะปกติหากเราเอาอาเรย์มาใช้ในนิพจน์การเปรียบเทียบก็จะคืนค่าออกมา เป็นอาเรย์ของข้อมูลชนิดบูล
print(z>3) # ได้ [False False False False True True]
print(z%2==1) # ได้ [False True False True False True]
print(z%2==1) # ได้ [False True False True False True]
ดังนั้นหากนำผลที่ได้จากนิพจน์นี้ไปใช้เป็นดัชนีในการเข้าถึงสมาชิกในอาเรย์ละก็ จะได้อาเรย์ที่มีสมาชิกเหลือแค่ตัวที่เข้าเงื่อนไข
print(z[z>3]) # ได้ [4 5]
print(z[z%2==1]) # ได้ [1 3 5]
print(z[z%2==1]) # ได้ [1 3 5]
ผลที่ได้ก็คือเป็นการคัดกรองสมาชิกภายในอาเรย์ให้เหลือเฉพาะบางส่วน การเขียนแบบนี้จึงมีประโยชน์มาก หากประยุกต์ให้ดีจะสามารถสร้างอาเรย์ในแบบที่ต้องการได้ง่ายมาก
ตัวอย่างการประยุกต์ใช้ เช่นลองคัดกรองข้อมูลบางส่วนที่เข้าเงื่อนไข แบ่งเอาไว้เป็นส่วนหนึ่ง ส่วนที่ไม่เข้าเงื่อนไขก็ไว้อีกส่วนหนึ่ง
เช่นลองแบ่งกราฟ sin ออกเป็น ๒ ส่วน ส่วนที่ค่าสูงกว่าและต่ำกว่า 0.4
import matplotlib.pyplot as plt
x = np.linspace(-15,15,10001)
y = np.cos(x)
plt.plot(x[y<0.4],y[y<0.4],'--',lw=2)
plt.plot(x[y>=0.4],y[y>=0.4],'r',lw=2)
plt.show()
x = np.linspace(-15,15,10001)
y = np.cos(x)
plt.plot(x[y<0.4],y[y<0.4],'--',lw=2)
plt.plot(x[y>=0.4],y[y>=0.4],'r',lw=2)
plt.show()

หรืออาจใช้เงื่อนไขเป็นทั้งแกน x และ y ร่วมกัน เช่นคัดกรองจุดที่อยู่ภายในรัศมี 0.7 จากใจกลางออกไป
x = np.linspace(-1,1,4001)
y = np.cos(x*50)
plt.figure(figsize=[7,7])
plt.axes(aspect=1,xlim=[-1.1,1.1],ylim=[-1.1,1.1])
plt.scatter(x[x**2+y**2>0.7**2],y[x**2+y**2>0.7**2],s=30)
plt.show()
y = np.cos(x*50)
plt.figure(figsize=[7,7])
plt.axes(aspect=1,xlim=[-1.1,1.1],ylim=[-1.1,1.1])
plt.scatter(x[x**2+y**2>0.7**2],y[x**2+y**2>0.7**2],s=30)
plt.show()

เราสามารถใช้วิธีนี้เข้าถึงสมาชิกบางส่วนเพื่อไปแก้ไขบางส่วน
เช่น แก้ข้อมูลที่ติดลบให้เป็น 0 ให้หมด
ay = np.random.randint(-9,9,10)
print(ay) # ได้ [ 8 -4 0 1 -5 -1 5 -2 1 1]
ay[ay<0] = 0
print(ay) # ได้ [8 0 0 1 0 0 5 0 1 1]
print(ay) # ได้ [ 8 -4 0 1 -5 -1 5 -2 1 1]
ay[ay<0] = 0
print(ay) # ได้ [8 0 0 1 0 0 5 0 1 1]
ลองดูตัวอย่างโดยวาดกราฟซึ่งมีการตัดข้อมูลส่วนที่ต่ำกว่า 0 ให้กลายเป็น 0 ทั้งหมด
x = np.linspace(0,2,2001)
y = np.cos(100*x)+np.sin(110*x)
y[y<0] = 0
plt.axes(ylim=[-2,2])
plt.plot(x,y)
plt.show()
y = np.cos(100*x)+np.sin(110*x)
y[y<0] = 0
plt.axes(ylim=[-2,2])
plt.plot(x,y)
plt.show()

หากใช้ตัวแปรมารับอาเรย์ที่ได้จากการเข้าถึงด้วยดัชนีบูล จะมีการคัดลอกค่าทั้งหมดเข้าไปเก็บในตัวแปรนั้น ไม่ได้เกิดการถ่ายทอด กล่าวคือหากมีการเปลี่ยนแปลงค่าภายในตัวแปรใหม่นั้นจะไม่กระทบถึงข้อมูลภายในอาเรย์เดิม
print(ay) # ได้ [-3 7 -5 -7 7 3 8 5 -8 -1]
ayw = ay[ay<0]
print(ayw) # ได้ [-3 -5 -7 -8 -1]
ayw[:] = 0
print(aw) # ได้ [0 0 0 0 0]
print(ay) # ได้ [-3 7 -5 -7 7 3 8 5 -8 -1]
ayw = ay[ay<0]
print(ayw) # ได้ [-3 -5 -7 -8 -1]
ayw[:] = 0
print(aw) # ได้ [0 0 0 0 0]
print(ay) # ได้ [-3 7 -5 -7 7 3 8 5 -8 -1]
ซึ่งจะเห็นว่าต่างจากการใช้ดัชนีเป็นเลขธรรมดาซึ่งมีคุณสมบัติการถ่ายทอด ดังนั้นต้องระวังอย่าสับสนกัน
ดัชนีในสองมิติ
กรณีที่ใช้ในสองมิติขึ้นไปจะมีความซับซ้อนขึ้นมาแต่หากเข้าใจแล้วก็จะประยุกต์ใช้ได้ดี
ก่อนอื่นทวนเนื้อหาจากบทที่แล้วสักหน่อย อาเรย์สองมิติประกอบไปด้วยแถว (แนวตั้ง) กับหลัก (แนวนอน)
ขอใช้อาเรย์นี้เป็นตัวอย่าง
z = np.array([[0,1,2,3],[10,11,12,13],[20,21,22,23]])
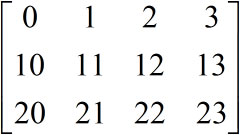
การเข้าถึงสมาชิกในอาเรย์สามารถใช้ลิสต์ของดัชนี โดยใช้เป็น [แถว,หลัก]
print(z[2,1]) # ได้ 21
ถ้าใส่แทนเลขหลักด้วย : หรือไม่ใส่เลย จะเป็นการเลือกเอาสมาชิกจากทุกหลักในแถวนั้น
print(z[2,:]) # ได้ [20 21 22 23]
print(z[2]) # ได้ [20 21 22 23]
print(z[2]) # ได้ [20 21 22 23]

แต่ถ้าใส่แทนเลขหลักด้วย : หรือไม่ใส่เลย และใส่แทนเลขแถวด้วยลิสต์ จะเป็นการเลือกเอาหลักที่มีดัชนีเป็นทุกตัวในลิสต์นั้น
print(z[[1,2],:])
# ได้
# [[10 11 12 13]
# [20 21 22 23]]
print(z[[1,2]])
# ได้
# [[10 11 12 13]
# [20 21 22 23]]
# ได้
# [[10 11 12 13]
# [20 21 22 23]]
print(z[[1,2]])
# ได้
# [[10 11 12 13]
# [20 21 22 23]]
ถ้าใส่แทนเลขแถวด้วย : ใส่แทนหลักด้วยตัวเลขจะกลายเป็นการเลือกเอาสมาชิกจากทุกแถวในหลักนั้น
print(z[:,1]) # ได้ [ 1 11 21]

แต่ถ้าใส่แทนเลขแถวด้วย : แทนหลักด้วยลิสต์ ผลที่จะเป็นการเลือกเอาแถวที่มีดัชนีเป็นทุกตัวในลิสต์นั้นมาพร้อมกัน
print(z[:,[1,2]])
# ได้
# [[ 1 2]
# [11 12]
# [21 22]]
# ได้
# [[ 1 2]
# [11 12]
# [21 22]]

จากตรงนี้ เราลองเปลี่ยนมาลองใช้อาเรย์ชนิดบูลในการเข้าถึงสมาชิกในอาเรย์เช่นเดียวกับที่ทำในหนึ่งมิติ
ลองสร้างอาเรย์ที่เก็บค่าความจริงเท็จขึ้นมา จากนั้นลองนำไปใช้เป็นตัวระบุดัชนีในอาเรย์ z
fft = np.array([False,False,True])
print(fft) # ได้ [False False True]
print(z[fft]) # ได้ [[20 21 22 23]]
print(z[fft,:]) # ได้ [[20 21 22 23]]
print(fft) # ได้ [False False True]
print(z[fft]) # ได้ [[20 21 22 23]]
print(z[fft,:]) # ได้ [[20 21 22 23]]

ซึ่งมีค่าเท่ากับ z[2] หรือ z[2,:]
จะเห็นว่าอาเรย์ fft ในที่นี้เป็นตัวระบุว่าจะเอาสมาชิกในแถวไหนของ z
ถ้าหากมี True อยู่ ๒ ตัว ก็จะได้ออกมา ๒ แถว
tft = np.array([True,False,True])
print(tft) # ได้ [ True False True]
print(z[tft]) # หรือ print(z[tft,:]) ก็ได้
# ได้
# [[ 0 1 2 3]
# [20 21 22 23]]
print(tft) # ได้ [ True False True]
print(z[tft]) # หรือ print(z[tft,:]) ก็ได้
# ได้
# [[ 0 1 2 3]
# [20 21 22 23]]

ซึ่งมีค่าเท่ากับ z[[1,2]] หรือ z[[1,2],:]
หากใช้วิธีเดียวกันแทนเลขหลักก็ได้ผลในลักษณะเดียวกัน
fftf = np.array([False,False,True,False])
print(fftf) # ได้ [False False True False]
print(z[:,fftf])
# ได้
# [[ 2]
# [12]
# [22]]
tftf = np.array([True,False,True,False])
print(tftf) # ได้ [ True False True False]
print(z[:,tftf])
# ได้
# [[ 0 2]
# [10 12]
# [20 22]]
print(fftf) # ได้ [False False True False]
print(z[:,fftf])
# ได้
# [[ 2]
# [12]
# [22]]
tftf = np.array([True,False,True,False])
print(tftf) # ได้ [ True False True False]
print(z[:,tftf])
# ได้
# [[ 0 2]
# [10 12]
# [20 22]]

ทีนี้อาเรย์มีคุณสมบัติการกระจาย ถ้าหากเอาอาเรย์มาเทียบกับค่าอะไรบางอย่างก็สามารถได้ผลออกมาเป็นอาเรย์ของค่าความจริงเท็จ
print(z==21)
# ได้
# [[False False False False]
# [False False False False]
# [False True False False]]
# ได้
# [[False False False False]
# [False False False False]
# [False True False False]]
จะเห็นว่าในนี้มีแค่สมาชิกตัวเดียวที่มีค่าเป็น 21 จึงคืนค่าเป็น True ที่เหลือเป็น False
ถ้าใช้วิธีนี้กับบางส่วนของอาเรย์ก็จะได้อาเรย์ของค่าความจริงเท็จที่มีมิติเดียว
print(z[2,:]==21) # ได้ [False True False False]
ซึ่งเป็นสิ่งที่สามารถถูกนำมาใช้เป็นค่าดัชนีได้
ดังนั้นหากนำมาประยุกต์เราจะสามารถใช้เพื่อคัดกรองสมาชิกได้
print(z[:,z[2,:]==21]) # เอาอาเรย์หลักที่มีสมาชิกแถว 2 เป็น 21
# ได้
# [[ 1]
# [11]
# [21]]
print(z[z[:,2]==22,:]) # เอาอาเรย์แถวที่มีสมาชิกหลัก 2 เป็น 22
# ได้ [[20 21 22 23]]
print(z[z[:,2]>11,:]) # เอาอาเรย์แถวที่มีสมาชิกหลัก 2 มากกว่า 11
# ได้
# [[10 11 12 13]
# [20 21 22 23]]
print(z[:,z[2,:]%10>1]) # เอาอาเรย์หลักที่มีสมาชิกแถว 2 หาร 10 แล้วเหลือเศษมากกว่า 1 (ก็คือมีเลขหลักหน่วยเป็น 2 ขึ้นไป)
# ได้
# [[ 2 3]
# [12 13]
# [22 23]]
# ได้
# [[ 1]
# [11]
# [21]]
print(z[z[:,2]==22,:]) # เอาอาเรย์แถวที่มีสมาชิกหลัก 2 เป็น 22
# ได้ [[20 21 22 23]]
print(z[z[:,2]>11,:]) # เอาอาเรย์แถวที่มีสมาชิกหลัก 2 มากกว่า 11
# ได้
# [[10 11 12 13]
# [20 21 22 23]]
print(z[:,z[2,:]%10>1]) # เอาอาเรย์หลักที่มีสมาชิกแถว 2 หาร 10 แล้วเหลือเศษมากกว่า 1 (ก็คือมีเลขหลักหน่วยเป็น 2 ขึ้นไป)
# ได้
# [[ 2 3]
# [12 13]
# [22 23]]
หากนำทั้งอาเรย์มาเข้านิพจน์หาค่าความจริงเท็จก็จะได้อาเรย์ของ True False ที่มีขนาดตามนั้น เช่น
ay = np.random.randint(0,100,[4,4])
print(ay)
# ได้
# [[50 61 5 63]
# [57 10 80 82]
# [25 30 10 24]
# [53 61 36 71]]
print(ay>50)
# ได้
# [[False True False True]
# [ True False True True]
# [False False False False]
# [ True True False True]]
print(ay)
# ได้
# [[50 61 5 63]
# [57 10 80 82]
# [25 30 10 24]
# [53 61 36 71]]
print(ay>50)
# ได้
# [[False True False True]
# [ True False True True]
# [False False False False]
# [ True True False True]]
ซึ่งเมื่อเราเอาอาเรย์ที่ได้ตัวนี้มาเป็นดัชนีให้กับตัวอาเรย์นั้นเอง ผลที่ได้จะออกมาในรูปของอาเรย์หนึ่งมิติซึ่งประกอบด้วยสมาชิกเฉพาะส่วนที่เป็น True
print(ay[ay>50]) # ได้ [61 63 57 80 82 53 61 71]
ซึ่งจะเห็นว่าแบบนี้ทำให้สูญเสียมิติไป อย่างไรก็ตามแม้จะอยู่ในรูปหนึ่งมิติแต่อาเรย์ตัวนี้ก็ชี้ถึงสมาชิกแต่ละตัวในอาเรย์ตัวเดิมนี้อยู่ เราสามารถทำการแก้ข้อมูลมันได้
ay[ay>50] = 0
print(ay)
# ได้
# [[50 0 5 0]
# [ 0 10 0 0]
# [25 30 10 24]
# [ 0 0 36 0]]
print(ay)
# ได้
# [[50 0 5 0]
# [ 0 10 0 0]
# [25 30 10 24]
# [ 0 0 36 0]]
เท่านี้ตัวเลขที่มีค่ามากกว่า 50 ก็ถูกเปลี่ยนให้กลายเป็น 0 หมด
การใช้อาเรย์ของจำนวนเต็มเป็นดัชนี
อาเรย์ของข้อมูลชนิดจำนวนเต็ม รวมทั้งลิสต์ของจำนวนเต็ม สามารถใช้เพื่อเป็นดัชนีเพื่ออ้างอิงถึงสมาชิกในอาเรย์ได้ โดยจะเป็นการเข้าถึงสมาชิกทีละหลายตัวตามตัวเลขที่ระบุไว้นั้น
ตัวอย่าง
az = np.arange(0,100,10)
print(az) # [ 0 10 20 30 40 50 60 70 80 90]
print(az[[2,3,7]]) # [20 30 70]
ai = np.array([3,5,6]) # สร้างอาเรย์เพื่อใช้เป็นดัชนี
print(az[ai]) # ได้ [30 50 60]
print(az) # [ 0 10 20 30 40 50 60 70 80 90]
print(az[[2,3,7]]) # [20 30 70]
ai = np.array([3,5,6]) # สร้างอาเรย์เพื่อใช้เป็นดัชนี
print(az[ai]) # ได้ [30 50 60]
การใช้ในลักษณะนี้มีประโยชน์มาก สามารถเอาไปประยุกต์ใช้เช่นเวลาที่มีข้อมูลที่ยาวมากๆแล้วต้องการจะยกแต่บางส่วนออกมาเป็นช่วงๆ
เช่น เวลาที่ต้องการวาดแค่บางจุดบนกราฟ
x = np.arange(10001)
y = np.sin(x/500.)
plt.plot(x,y) # กราฟเส้นของข้อมูลทั้งหมด
ai = np.arange(0,10001,200) # อาเรย์ที่ใช้เป็นดัชนี
plt.plot(x[ai],y[ai],'o') # กราฟจุดของข้อมูลที่กรองแล้ว
plt.show()
y = np.sin(x/500.)
plt.plot(x,y) # กราฟเส้นของข้อมูลทั้งหมด
ai = np.arange(0,10001,200) # อาเรย์ที่ใช้เป็นดัชนี
plt.plot(x[ai],y[ai],'o') # กราฟจุดของข้อมูลที่กรองแล้ว
plt.show()

จะเห็นว่ามีข้อมูล 10001 ตัวที่ประกอบกันเป็นกราฟ sin แต่เราต้องการนำข้อมูลแค่บางส่วน โดยในที่นี้ให้วาดจุดแค่ทุก 200 ค่า กรณีแบบนี้ดัชนีแฟนซีจะมีประโยชน์มาก
กรณีที่มีการนำตัวแปรมารับค่าอาเรย์ที่ได้จากดัชนีแฟนซีก็จะได้ผลเช่นเดียวกับดัชนีบูลก็คือเป็นการคัดลอกอาเรย์ไปเก็บไว้ในตัวแปรใหม่ ไม่ใช่การถ่ายทอด หากมีการแก้ไขค่าอะไรในตัวแปรใหม่ก็จะไม่กระทบถึงอาเรย์ตัวเดิม
เรื่องของดัชนีแฟนซีนี้อาจจะเข้าใจยาก แต่หากใช้จนคล่องแล้วมันจะเป็นวิธีการในการคัดกรององค์ประกอบที่ทรงพลังมาก ยังไงก็คงจะพยายามเข้าใจมันสักหน่อย
np.where
เราสามารถใช้ฟังก์ชัน np.where เพื่อหาค่าดัชนีของสมาชิกภายในอาเรย์ที่เข้ากับเงื่อนไขบางอย่างที่ต้องการได้
np.where ต้องการอาร์กิวเมนต์เป็นนิพจน์ของอาเรย์ซึ่งให้ค่าความจริงเท็จ เช่น x>10 x==20 x!=3 เป็นต้น จากนั้นจะคืนค่าออกมาเป็นดัชนีของอาเรย์นั้นที่เข้าเงื่อนไข (ให้ผลค่าความจริงเป็นจริง)
ตัวอย่าง
a = np.linspace(10,13,6)
print(a) # ได้ [ 10. 10.6 11.2 11.8 12.4 13. ]
print(a>11) # ได้ [False False True True True True]
print(np.where(a>11)) # ได้ (array([2, 3, 4, 5]),)
print(a) # ได้ [ 10. 10.6 11.2 11.8 12.4 13. ]
print(a>11) # ได้ [False False True True True True]
print(np.where(a>11)) # ได้ (array([2, 3, 4, 5]),)
จะเห็นว่า np.where(a>11) จะได้ผลออกมาเป็นอาเรย์ที่ประกอบไปด้วยเลขดัชนีของสมาชิกใน a ที่ให้ a>11 เป็น True
จากนั้นหากเอาผลที่ได้จาก np.where นี้มาใช้เป็นดัชนี
print(a[np.where(a>11)]) # ได้ [ 11.2 11.8 12.4 13. ]
จะเห็นว่าผลที่ได้จะเหมือนกับ a[a>11]
print(a[a>11]) # ได้ [ 11.2 11.8 12.4 13. ]
ซึ่งถ้าหากนำมาใช้ในลักษณะนี้ก็อาจดูไม่จำเป็น เพราะทำให้เขียนยาวขึ้นแต่ผลเหมือนเดิม
นอกจากนี้แล้ว np.where มีวิธีการใช้งานที่มากกว่านั้น ซึ่งทำได้โดยใส่อาร์กิวเมนต์เพิ่มเป็นสามตัว แบบนั้นจะเป็นการนำอาเรย์ตัวเดิมมาจัดการอะไรบางอย่างโดยขึ้นกับเงื่อนไขที่ ใส่ลงไป
การทำงานอาจเข้าใจยากเล็กน้อย ลองดูตัวอย่างเพื่อให้พอเห็นภาพ
a = np.linspace(10,13,6)
print(a) # ได้ [ 10. 10.6 11.2 11.8 12.4 13. ]
print(np.where(a>11,1,2)) # ได้ [2 2 1 1 1 1]
print(a) # ได้ [ 10. 10.6 11.2 11.8 12.4 13. ]
print(np.where(a>11,1,2)) # ได้ [2 2 1 1 1 1]
จะเห็นว่าการทำงานของ np.where ในที่นี้ก็คือจะพิจารณาค่าความจริงเท็จจากอาร์กิวเมนต์ตัวที่หนึ่ง ถ้าหากว่าเป็นจริงก็จะคืนค่าออกมาตามค่าที่ใส่ไว้ในอาร์กิวเมนต์ตัวที่สอง ถ้าเป็นเท็จก็จะคืนค่าตามอาร์กิวเมนต์ตัวที่สาม
ในที่นี้จะเห็นว่า สมาชิก ๒ ตัวแรกคือ 10. กับ 10.6 ไม่เข้าเงื่อนไข (ให้ค่า False) จึงได้รับค่าที่อยู่ในอาร์กิวเมนต์ตัวที่สาม ก็คือ 2 ส่วนที่เหลือเป็น True จึงได้ค่า 1
ค่าที่ใส่นั้นอาจไม่ใช่แค่จำนวนค่าคงที่เท่านั้นแต่สามารถใส่ตัวอาเรย์ตัวนั้นเพื่อให้มันนำเอาสมาชิกในลำดับที่ตรงกันมาคำนวณ
เช่น
print(np.where(a>11,a+10,a-10)) # [ 0. 0.6 21.2 21.8 22.4 23. ]
ในที่นี้สมาชิกใน a สองตัวแรกไม่เข้าเงื่อนไข a>11 จึงได้ค่าเป็น a-10 ค่าจึงลดลงไป 10 ส่วนตัวที่เหลือเข้าเงื่อนไขจึงบวกไป 10
อาเรย์ที่ใช้เป็นเงื่อนไขในอาร์กิวเมนต์ตัวแรกกับอาเรย์ที่ใช้พิจารณาค่าอาจไม่ใช่ตัวเดียวกันก็ได้ ขอแค่มีสมาชิกจำนวนเท่ากัน
ตัวอย่าง
b = np.linspace(20,24,6)
c = np.arange(1,7)
print(b) # ได้ [ 20. 20.8 21.6 22.4 23.2 24. ]
print(c) # ได้ [1 2 3 4 5 6]
print(c%2==0) # ได้ [False True False True False True]
print(np.where(c%2==0,b,b/5)) # ได้ [ 4. 20.8 4.32 22.4 4.64 24. ]
c = np.arange(1,7)
print(b) # ได้ [ 20. 20.8 21.6 22.4 23.2 24. ]
print(c) # ได้ [1 2 3 4 5 6]
print(c%2==0) # ได้ [False True False True False True]
print(np.where(c%2==0,b,b/5)) # ได้ [ 4. 20.8 4.32 22.4 4.64 24. ]
ในตัวอย่างนี้ใช้ c เป็นเงื่อนไขโดยจะเห็นว่าตัวที่ 0,2,4 เป็น False ส่วน b ถูกใช้เป็นอาเรย์สำหรับนำค่ามาคำนวณ ค่าที่ได้จาก np.where ในที่นี้จะเป็นค่าของสมาชิกใน b ในตำแหน่งที่ได้ True ส่วนตำแหน่งที่ได้ False จะถูกหาร 5
และในบางครั้งอาจใช้เพื่อคัดเลือกว่าจะเอาค่าจากอาเรย์ตัวไหนตามเงื่อนไขที่กำหนดก็ได้
d = np.array([1100,1200,1300,1400])
e = np.array([11,12,13,14])
f = np.array([1,9,8,1])
print(np.where(f>1,e,d)) # ได้ [1100 12 13 1400]
e = np.array([11,12,13,14])
f = np.array([1,9,8,1])
print(np.where(f>1,e,d)) # ได้ [1100 12 13 1400]
เราอาจนำมาใช้เพื่อกรองค่าในฟังก์ชันบางส่วนที่ไม่ตรงเงื่อนไขที่ต้องการ ตัวอย่างเช่นลองสร้างกราฟของฟังก์ชัน sin โดยที่ให้ค่าที่ต่ำกว่า 0 เป็น 0 ไปให้หมด
x = np.arange(0,20,0.01)
y = np.sin(x)
y2 = np.where(y<0,0,y)
plt.subplot(211,ylim=[-1,1])
plt.plot(x,y)
plt.subplot(212,ylim=[-1,1])
plt.plot(x,y2)
plt.show()
y = np.sin(x)
y2 = np.where(y<0,0,y)
plt.subplot(211,ylim=[-1,1])
plt.plot(x,y)
plt.subplot(212,ylim=[-1,1])
plt.plot(x,y2)
plt.show()

np.select
มีอีกฟังก์ชันซึ่งคล้ายๆกับ np.where สามารถทำให้ได้ผลที่เหมือนกันได้ นั่นคือ np.select
ฟังก์ชันนี้จะทำการสร้างอาเรย์ใหม่ขึ้นมาจากอาเรย์เดิมที่ใช้เป็นตัวกำหนดเงื่อนไข ซึ่งจะใส่เป็นอาร์กิวเมนต์ตัวแรก ค่าในอาเรย์ที่สร้างขึ้นใหม่จะกำหนดโดยอาร์กิวเมนต์ตัวหลัง
x = np.array([1.1,1.3,1.6,1.7,2.1,2.4])
print(np.select([x>1.5,x<=1.5],[3,4])) # ได้ [4 4 3 3 3 3]
print(np.select([x>1.5,x<=1.5],[3,4])) # ได้ [4 4 3 3 3 3]
ในตัวอย่างนี้สมาชิกใน x สองตัวแรก 1.1,1.3 นั้นน้อยว่า 1.5 จึงเข้าเงื่อนไขหลังจึง
เงื่อนไขแรกกับเงื่อนไขหลังไม่จำเป็นต้องครอบคลุมทุกสิ่งที่เป็นไปได้ หากมีสมาชิกไหนที่ไม่เข้ากับเงื่อนไขเลยก็จะได้ค่า 0 เช่น
print(np.select([x>1.5,x<=1.2],[3,4])) # ได้ [4 0 3 3 3 3]
เงื่อนไขอาจมีกี่ตัวก็ได้ ซึ่งก็จะต้องเตรียมค่าที่จะใช้เมื่อเข้าเงื่อนไขนั้นให้มีจำนวนเท่ากันด้วย
print(np.select([x>1.8,x>1.5,x<=1.5],[2,3,4])) # ได้
ค่าในลิสต์ตัวหลังก็อาจใช้เป็นอาเรย์ตัวที่พิจารณาเองได้
print(np.select([x>1.8,x>1.5,x<=1.5],[2*x,0,4*x])) # ได้ [ 4.4 5.2 0. 0. 4.2 4.8]
และก็อาจใช้เป็นอาเรย์ตัวอื่นที่มีขนาดเท่ากัน
x = np.array([1.1,1.3,1.6,1.7,2.1,2.4])
a = np.array([100,200,300,400,500,600])
b = np.array([10,20,30,40,50,60])
c = np.array([1,2,3,4,5,6])
print(np.select([x>1.8,x>1.5,x<=1.5],[a*x,b*x,c*x])) # ได้ [ 1100. 2600. 480. 680. 105. 144.]
a = np.array([100,200,300,400,500,600])
b = np.array([10,20,30,40,50,60])
c = np.array([1,2,3,4,5,6])
print(np.select([x>1.8,x>1.5,x<=1.5],[a*x,b*x,c*x])) # ได้ [ 1100. 2600. 480. 680. 105. 144.]
เราอาจประยุกต์ใช้เพื่อทำกราฟที่มีค่าแบ่งเป็นช่วงๆก็ได้
x = np.linspace(-2,4,600)
y = x**2
y2 = np.select([x<-1,x<=3,x>3],[1,y,9])
plt.figure(figsize=[6,8])
plt.subplot(211,ylim=[-1,10],title='$y=x^2$')
plt.plot(x,y)
plt.subplot(212,ylim=[-1,10],title=r'$y=1|x\leq-1,x^2|x\in(-1,3],9|x>3$')
plt.plot(x,y2)
plt.subplots_adjust(0.05,0.05,0.96,0.95,0.4,0.4)
plt.show()
y = x**2
y2 = np.select([x<-1,x<=3,x>3],[1,y,9])
plt.figure(figsize=[6,8])
plt.subplot(211,ylim=[-1,10],title='$y=x^2$')
plt.plot(x,y)
plt.subplot(212,ylim=[-1,10],title=r'$y=1|x\leq-1,x^2|x\in(-1,3],9|x>3$')
plt.plot(x,y2)
plt.subplots_adjust(0.05,0.05,0.96,0.95,0.4,0.4)
plt.show()

np.choose
ฟังก์ชัน np.choose มีไว้สร้างอาเรย์ขึ้นจากรายการ (ลิสต์หรืออาเรย์) ของเลขดัชนี และรายการของค่าที่ต้องการนำมาใช้
เพื่อให้เข้าใจจำเป็นต้องดูตัวอย่างการใช้
s = np.array([1,1,1,2,2,0,1,3]) # อาเรย์เก็บดัชนีตัวเลือก
g = np.array([0.1,3.1,5.1,6.1]) # อาเรย์เก็บค่าที่จะใช้
print(np.choose(s,g)) # ได้ [ 3.1 3.1 3.1 5.1 5.1 0.1 3.1 6.1]
g = np.array([0.1,3.1,5.1,6.1]) # อาเรย์เก็บค่าที่จะใช้
print(np.choose(s,g)) # ได้ [ 3.1 3.1 3.1 5.1 5.1 0.1 3.1 6.1]
จากตัวอย่างนี้จะเป็นการสร้างอาเรย์ที่ใช้อาร์กิวเมนต์ตัวแรกเป็นเลขดัชนีและ ตัวหลังเป็นค่าที่จะให้นำมาใช้เมื่อถูกอ้างอิงจากดัชนี ผลลัพธ์ที่ได้จะมีจำนวนสมาชิกเท่ากับอาเรย์ที่เก็บดัชนีตัวเลือก
จริงๆแล้วเราสามารถได้ผลแบบเดียวกันนี้ด้วยการเขียนง่ายๆเป็น g[s]
print(g[s]) # ได้ [ 3.1 3.1 3.1 5.1 5.1 0.1 3.1 6.1]
ซึ่งก็เป็นไปตามหลักของดัชนีแฟนซี
อ้างอิง
http://www.turbare.net/transl/scipy-lecture-notes/intro/numpy/operations.html
http://oppython.hatenablog.com/entry/2014/01/19/054931
http://kaiseki-web.lhd.nifs.ac.jp/documents/Python/array.htm
http://ism1000ch.hatenablog.com/entry/2014/01/15/025328
http://kaisk.hatenadiary.com/entry/2015/02/19/224531
http://oppython.hatenablog.com/entry/2014/01/19/054931
http://kaiseki-web.lhd.nifs.ac.jp/documents/Python/array.htm
http://ism1000ch.hatenablog.com/entry/2014/01/15/025328
http://kaisk.hatenadiary.com/entry/2015/02/19/224531