ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๒๒: การแจกแจงดีริคเล

เขียนเมื่อ 2020/09/12 14:09

แก้ไขล่าสุด 2024/10/03 19:39

ต่อจาก บทที่ ๒๑

ในบทนี้เป็นเรื่องของการแจกแจงดีริคเล (狄利克雷分布, Dirichlet distribution)

ฟังก์ชันการแจกแจงความน่าจะเป็นของการแจกแจงดีริคเล

การแจกแจงดีริคเล เป็นการแจกความน่าจะเป็นก่อนหน้าสังยุคของการแจกแจงอเนกนาม

ลักษณะความสัมพันธ์เช่นเดียวกับที่การแจกแจงเบตาเป็นการแจกแจงความน่าจะเป็นก่อนหน้าสังยุคของการแจกแจงทวินาม ดังนั้นอาจถือว่าเป็นการแจกแจงเบตาในกรณีหลายหมวดหมู่นั่นเอง

ฟังก์ชันการแจกแจงเป็นดังนี้

$\begin{align} P(\vec{x}) = \frac{1}{B(α_1,α_2,\cdots,α_m)}\prod_{i=1}^{m}x_i^{α_i-1} \end{align}$

โดยในที่นี้ B คือฟังก์ชันเบตาแบบหลายมิติ นิยามโดย

$\begin{align} B(α_1,α_2,\cdots,α_m)=\frac{\prod_{i=1}^m Γ(α_i)}{Γ(\sum_{i=1}^m α_i)} \end{align}$

ในที่นี้ $\vec{x}$ คือความน่าจะเป็นของหมวดต่างๆ (คือ $\vec{p}$ ในการแจกแจงอเนกนาม) มีทั้งหมด m หมวด รวมกันทุกตัวต้องเป็น 1

$\begin{align} \sum_{i=1}^m x_i = 1 \end{align}$

พารามิเตอร์ในที่นี้คือ $\vec{α}$ เรียกว่าเป็นพารามิเตอร์ความเข้มข้น (集中度参数, concentration parameter) ไม่ใช่เลขตัวเดียงแต่มีทั้งหมด m ตัว เท่ากับจำนวนหมวดหมู่ที่พิจารณา ทุกตัวเป็นจำนวนจริงบวก เป็นค่าที่บอกถึงน้ำหนักความสำคัญของแต่ละหมวดหมู่

$\begin{align} \vec{α} = \begin{bmatrix} α_1 \\ α_2 \\ \cdots \\ α_m \end{bmatrix} \end{align}$

หาก m=2 ซึ่งหมายถึงมีแค่ 2 หมวดหมู่แล้ว

$\begin{align} P(\vec{x}) = \frac{1}{B(α_1,α_2)}x_1^{α_1-1}x_2^{α_2-1} \end{align}$

ซึ่งถ้าแทน α₁ ด้วย α และแทน α₁ ด้วย β ก็จะกลายเป็นการแจกแจงเบตา ดังนั้นตรงนี้ก็พิสูจน์ได้ว่าการแจกแจงเบตาก็คือรูปแบบหนึ่งของการแจกแจงดีริคเลในกรณีที่มีแค่ 2 หมวดหมู่

สำหรับความหมายของ $\vec{α}$ ในการแจกแจงดีริคเลก็จะเหมือนกับ α และ β ในการแจกแจงเบตา แต่คราวนี้ไม่ได้มีแค่ 2 ตัว แต่มีจำนวนตัวแปรมากเท่าจำนวนหมวดหมู่

ค่าคาดหมายและส่วนเบี่ยงเบนมาตรฐานของการแจกแจงดีริคเล

ค่าคาดหมายของแต่ละหมวดหมู่ในการแจกแจงรีริคเลก็คือ

$\begin{align} E(x_i) = \frac{α_i}{α_Σ} \end{align}$

โดยในที่นี้ให้ $α_Σ$ แทนผลรวมของ α ทั้งหมด

$\begin{align} α_Σ = \sum_{i=1}^k α_i \end{align}$

ค่าความแปรปรวนของแต่ละหมวดหมู่คือ

$\begin{align} σ_i^{2} = \frac{α_i(α_Σ-α_i)}{(α_Σ)^2(α_Σ+1)} \end{align}$

ความแปรปรวนร่วมเกี่ยวระหว่างต่างหมวดหมู่คือ

$\begin{align} σ_{i,j}^{2} = \frac{-α_i α_j}{(α_Σ)^2(α_Σ+1)} \end{align}$

เมื่อ i≠j

เมทริกซ์ความแปรปรวนร่วมเกี่ยวได้เป็น

$\begin{align} Σ = \frac{1}{(α_Σ)^2(α_Σ+1)}\begin{bmatrix} α_1(α_Σ-α_1) & -α_1 α_2 & \cdots & -α_1 α_m \\ -α_2α_1 & α_2(α_Σ-α_2) & \cdots & -α_2α_m \\ \vdots & \vdots & \ddots & \vdots \\ -α_mp_1 & -α_mα_2 & \cdots & α_m(α_Σ-α_m) \end{bmatrix} \end{align}$

การแจกแจงความน่าจะเป็นของพารามิเตอร์ของการแจกแจงอเนกนาม

เพื่อพิสูจน์ว่าการแจกแจงดีริคเลเป็นการแจกแจงความน่าจะเป็นก่อนหน้าสังยุคของการแจกแจงอเนกนาม ในที่นี้จะทำเหมือนกับที่ทำกับการแจกแจงทวินามในบทที่ ๑๕ วิธีการจะคล้ายๆกันแค่เปลี่ยนจากการแจกแจงทวินามเป็นการแจกแจงอเนกนาม ดังนั้นจะไม่เขียนถึงรายละเอียดมากนัก

ในที่นี้จะเขียนแทนการแจกแจงดีริคเลด้วย $\mathcal{Dì}$ แบบนี้

$\begin{align} \mathcal{Dì}(\vec{p}|\vec{α}) &= \frac{1}{B(α_1,α_2,\cdots,α_m)}\prod_{i=1}^{m}p_i^{α_i-1} \\ &= \mathcal{C} \prod_{i=1}^{m}p_i^{α_i-1} \end{align}$

ในที่นี้ก็จะดึงส่วนที่ไม่เกี่ยวข้องกับ $\vec{p}$ มาใส่ไว้ใน $\mathcal{C}$ ให้หมดแล้วพิจารณาเฉพาะส่วนที่เหลือเพื่อความง่าย เช่นเดียวกับที่ทำมาในบทก่อนๆ

พิจารณาการแจกแจงของ $\vec{p}$ ซึ่งเป็นการแจกแจงอเนกนาม m หมวด สมมุติว่ามีผลการทดลองใหม่เข้ามาเป็น $\vec{k}_1 =\begin{bmatrix} k_{1,1} \\ k_{1,2} \\ \cdots \\ k_{1,m} \end{bmatrix}$ พิจารณาการแจกแจงความน่าจะเป็นภายหลังตามทฤษฎีบทของเบส์ได้ว่า

$\begin{align} \mathcal{P}(\vec{p}|\vec{k}_1) &= \frac{P(\vec{k}_1|\vec{p})\mathcal{P}(\vec{p})}{P(\vec{k}_1)} \\ &= \mathcal{C}P(\vec{k}_1|\vec{p})\mathcal{P}(\vec{p}) \end{align}$

ในส่วนของการแจกแจงก่อนหน้านั้นในที่นี้หากเริ่มจากไม่มีข้อมูลอะไรก็ให้เป็นค่าคงตัว ซึ่งก็คือ $\vec{α}=\vec{1}$ ทุกตัวมีค่าเป็น 1 ทั้งหมด

$\begin{align} \mathcal{P}(\vec{p}) &= \mathcal{Dì}(\vec{p}|\vec{1}) \\ &= \mathcal{C} \end{align}$

ส่วนฟังก์ชันควรจะเป็นในที่นี้เป็นการแจกแจงอเนกนาม

$\begin{align} P(\vec{k}|\vec{p}) &= n!\prod_{i=1}^m\frac{p_{1,i}^{k_{1,i}}}{k_{1,i}!} \\ &= \mathcal{C}\prod_{i=1}^m p_{1,i}^{k_{1,i}} \end{align}$

เมื่อเอามารวมกันก็ได้การแจกแจงความน่าจะเป็นภายหลังออกมา ซึ่งเขียนให้อยู่ในรูปของการแจกแจงดีริคเลได้ดังนี้

$\begin{align} \mathcal{P}(\vec{p}|\vec{k}_1) &= \mathcal{C}\prod_{i=1}^m p_{1,i}^{k_{1,i}} \\ &= \mathcal{Dì}\left(\vec{p}\left|\begin{bmatrix} k_{1,1}+1 \\ k_{1,2}+1 \\ \cdots \\ k_{1,m}+1 \end{bmatrix}\right.\right) \end{align}$

เท่านี้ก็คงจะพอมองออกได้ว่าต่อมาหากมีข้อมูลเข้ามาอีกหลายๆชุด เป็นจำนวน n ชุด ก็เอาค่า k ของแต่ละชุดมาบวกกันให้หมด

$\begin{align} \mathcal{P}(\vec{p}|\vec{k}_1,\vec{k}_2,\cdots,\vec{k}_n) &= \mathcal{Dì}\left(\vec{p}\left|\begin{bmatrix} \sum_{i=1}^n k_{i,1}+1 \\ \sum_{i=1}^n k_{i,2}+1 \\ \cdots \\ \sum_{i=1}^n k_{i,m}+1 \end{bmatrix}\right.\right) \end{align}$

และถ้าการแจกแจงก่อนหน้าไม่ใช่ 1 ทั้งหมด แต่มีค่า α ตั้งต้นอยู่แล้วเป็น α₀

$\begin{align} \mathcal{P}(\vec{p}) = \mathcal{Dì}(\vec{p}|\vec{α}_0) = \mathcal{Dì}\left(\vec{p}\left|\begin{bmatrix} α_{0,1} \\ α_{0,2} \\ \cdots \\ α_{0,m} \end{bmatrix}\right.\right) \end{align}$

แบบนั้นแล้วความน่าจะเป็นภายหลังก็จะมีค่า $\vec{α}_0$ เพิ่มเข้าไปอีกแทน 1 เป็น

$\begin{align} \mathcal{P}(\vec{p}|\vec{k}_1,\vec{k}_2,\cdots,\vec{k}_n) &= \mathcal{Dì}\left(\vec{p}\left|\begin{bmatrix} \sum_{i=1}^n k_{i,1}+α_{0,1} \\ \sum_{i=1}^n k_{i,2}+α_{0,2} \\ \cdots \\ \sum_{i=1}^n k_{i,m}+α_{0,m} \end{bmatrix}\right.\right) \end{align}$

การแจกแจงดีริคเลสามหมวดหมู่

เช่นเดียวกับที่ในบทที่ ๑๑ ได้อธิบายและแสดงการเปลี่ยนแปลงของการแจกแจงความน่าจะเป็นตามจำนวนข้อมูลที่เพิ่มเข้ามาด้วยฟังก์ชันเบตาไปแล้ว

บทนี้จะยกตัวอย่างกรณี 3 หมวดหมู่ ซึ่งเพิ่มเติมมาจากกรณี 2 หมวดหมู่ของการแจกแจงเบตา

ให้ $\vec{p}$ เป็นความน่าจะเป็นของแต่ละหมวดหมู่ แล้ว α ก็เป็นพารามิเตอร์ความเข้มข้นของหมวดหมู่นั้น

$\begin{align} \vec{p} = \begin{bmatrix} p_1 \\ p_2 \\ p_3 \end{bmatrix}, \vec{α} = \begin{bmatrix} α_1 \\ α_2 \\ α_3 \end{bmatrix} \end{align}$

ในที่นี้จะพิจารณาการแจกแจงค่า p₁ กับ p₂ ส่วน p₃ ก็จะถูกกำหนดค่าไปเองโดยอัตโนมัติ ตามเงื่อนไขที่ว่า

$\begin{align} p_3=1-p_1-p_2 \end{align}$

เริ่มแรก กรณีที่ไม่มีข้อมูลใดๆเลย การแจกแจงทั้งหมดจะเท่ากันหมด นั่นคือ α ทุกตัวเป็น 1

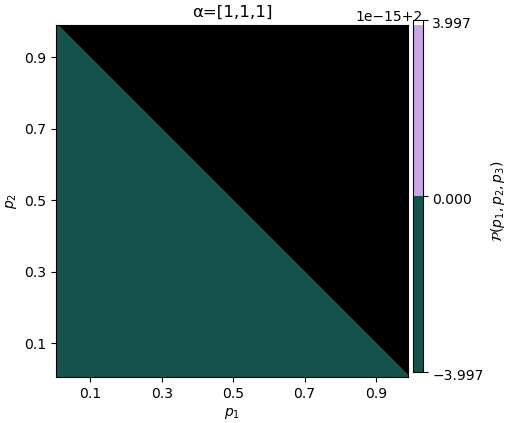
ในที่นี้การแจกแจงจะมีแค่ครึ่งล่างซ้าย เพราะถ้า p₁+p₂>1 จะทำให้ p₃ ติดลบ ซึ่งไม่มีอยู่จริง

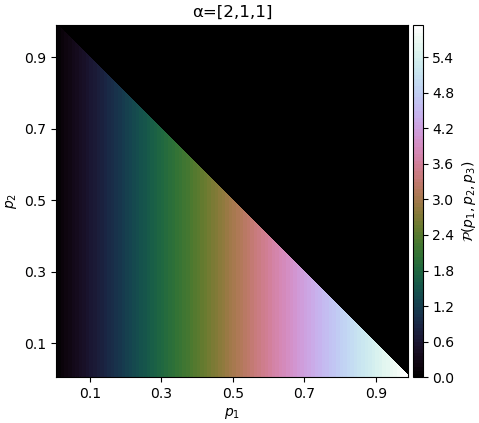
ต่อมาหากสุ่มครั้งแรกแล้วได้ผลลัพธ์เป็นหมวดหมู่ที่ 1 แล้ว ค่า α₁ ก็จะเพิ่มอีก 1 แล้วการแจกแจงความน่าจะเป็นก็จะกลายเป็นแปรตาม p₁

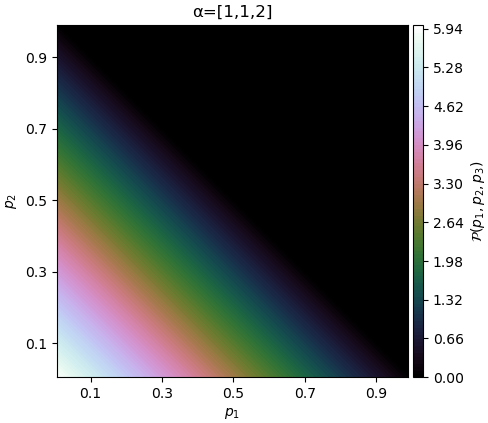
หรือถ้าหากเปลี่ยนเป็นได้ผลลัพธ์เป็นหมวดหมู่ที่ 3 แทน แบบนี้การแจกแจงความน่าจะเป็นก็จะแปรตาม p₃ ซึ่งก็คือ 1-p₁-p₂

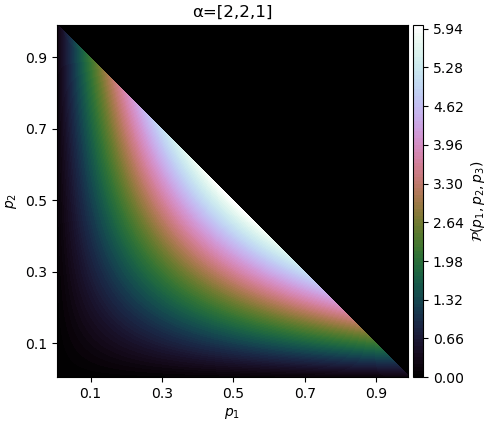
ถ้าได้ทั้งหมวดหมู่ที่ 1 และ 2 เพิ่มมาพร้อมกัน การแจกแจงก็จะเพิ่มตามค่า p₁ และ p₂

ถ้าเปลี่ยนเป็นได้หมวดหมู่ที่ 1 และ 3 แทน การแจกแจงก็เปลี่ยนไปเป็นทางนี้

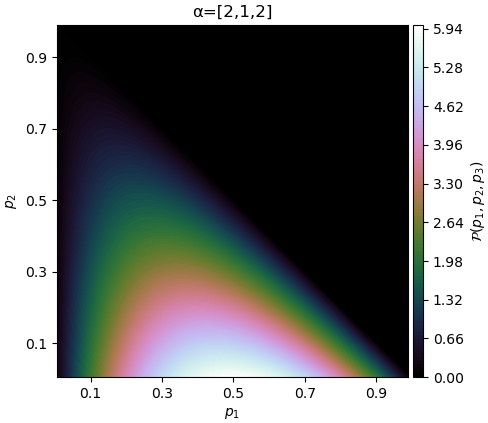
ถ้าแต่ละหมวดต่างก็เพิ่มมา 1 กลายเป็น 2 ทั้งหมด การแจกแจงตรงขอบก็จะเป็น 0 แล้วตรงกลางที่ 1/3 ก็จะมีค่าสูงขึ้นมา

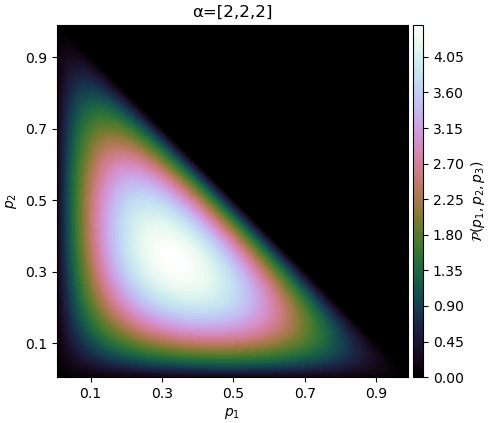
ถ้า α ตัวไหนมาก การแจกแจงก็จะเอนเอียงไปทางนั้นมาก

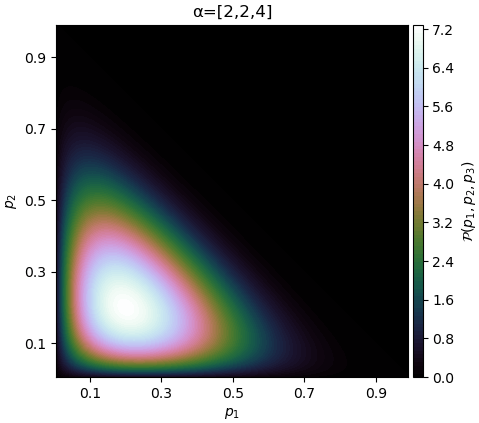
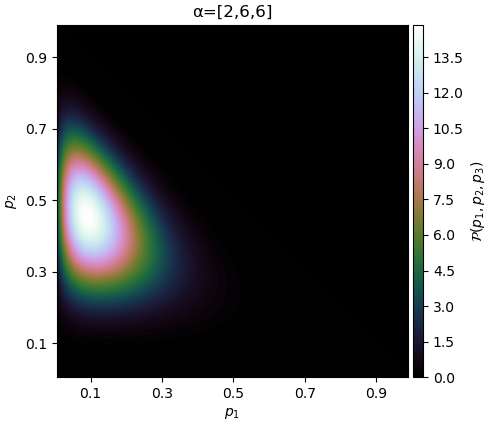
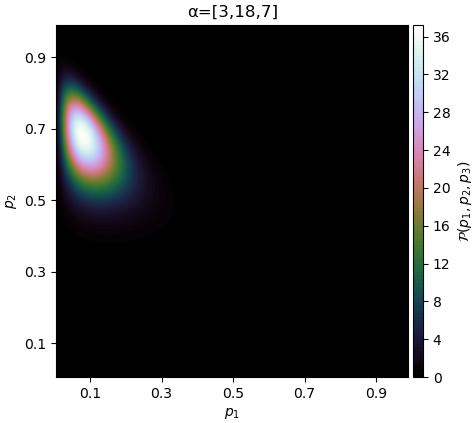
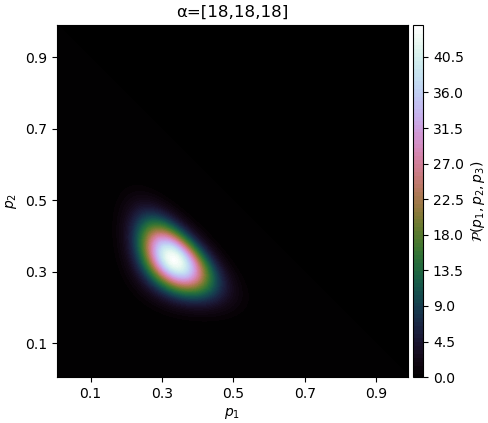
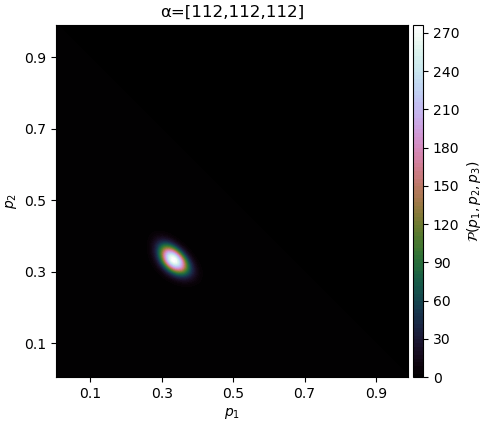
ถ้า α แต่ละตัวเท่าๆกัน แต่ค่าเพิ่มขึ้นเรื่อยๆ จุดสูงสุดก็ยังอยู่ที่ 1/3 แต่การแจกแจงจะยิ่งกองรวมกันตรงนั้นมากขึ้น

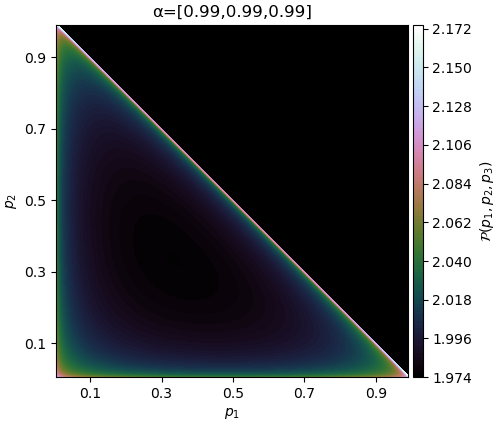
ในทางตรงกันข้าม ค่า α สามารถจะไม่เป็นจำนวนเต็ม ซึ่งจะเป็นค่าน้อยกว่า 1 ได้ด้วย ในกรณีนั้นจะกลายเป็นว่าตรงขอบค่าสูงกว่า

ลองทำเป็นภาพเคลื่อนไหวแสดงความเปลี่ยนแปลง เปรียบเทียบกรณีที่ α เท่ากันทั้ง 3 ตัว แต่ค่อยๆเพิ่มขึ้นไปพร้อมกัน

จะเห็นว่าเมื่อ α น้อยกว่า 1 ตรงกลางจะเว้า แล้วพอ α เป็น 1 ก็จะเรียบเท่ากันหมด แล้วพอ α มากกว่า 1 ก็จะเริ่มนูนตรงกลางแทน

-----------------------------------------

囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧

ดูสถิติของหน้านี้

หมวดหมู่

-- คณิตศาสตร์ >> ความน่าจะเป็น

ไม่อนุญาตให้นำเนื้อหาของบทความไปลงที่อื่นโดยไม่ได้ขออนุญาตโดยเด็ดขาด หากต้องการนำบางส่วนไปลงสามารถทำได้โดยต้องไม่ใช่การก๊อปแปะแต่ให้เปลี่ยนคำพูดเป็นของตัวเอง หรือไม่ก็เขียนในลักษณะการยกข้อความอ้างอิง และไม่ว่ากรณีไหนก็ตาม ต้องให้เครดิตพร้อมใส่ลิงก์ของทุกบทความที่มีการใช้เนื้อหาเสมอ

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

φυβλαςのβλογ
phyblas的博客

-----------------------------------------

囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧

หมวดหมู่

~ 自我介绍 ~

目录

按类别分日志

查看日志

最近

推荐日志

各月日志

2024年

2023年

2022年

2021年

2020年

找更早以前的日志

ไทย

日本語

中文

φυβλαςのβλογphyblas的博客

-----------------------------------------

囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧

หมวดหมู่

~ 自我介绍 ~

目录

按类别分日志

查看日志

最近

推荐日志

各月日志

2024年

2023年

2022年

2021年

2020年

找更早以前的日志

ไทย

日本語

中文

φυβλαςのβλογ
phyblas的博客

　查看日志

　最近

　推荐日志