maya python เบื้องต้น บทที่ ๒๑: การวิเคราะห์และคัดกรองส่วนประกอบ
เขียนเมื่อ 2016/03/11 13:52
แก้ไขล่าสุด 2021/09/28 16:42
ในบทที่แล้วเราได้พูดถึงการเปลี่ยนแปลงส่วนประกอบภายในซึ่งได้แก่จุดยอด เส้นขอบ และด้านของวัตถุแล้ว แต่ว่าวิธีนั้นก็มีปัญหาอยู่คือต้องมีการระบุตัวเลขของแต่ละส่วนประกอบ
ตัวเลขของส่วนประกอบเหล่านั้นแม้จะมีหลักตายตัว แต่บางทีก็ไม่ง่ายที่จะทำความเข้าใจได้ ไม่ใช่ว่าสามารถที่จะรู้ได้ตลอด ยิ่งเมื่อสร้างไปเรื่อยๆจะพบจุดยอดมากมาย ยากต่อการคาดเดามากขึ้น
การที่จะเลือกส่วนประกอบที่ต้องการได้โดยไม่จำเป็นต้องรู้หมายเลขนั้นง่าย ที่สุดก็คือการดูจากตำแหน่ง ว่าเราต้องการที่จะเลือกส่วนที่อยู่ตรงไหน
โดยปกติถ้าเป็นวัตถุถ้าหากเราต้องการหาตำแหน่งสามารถใช้ getAttr('.t') ได้ แต่ว่าวิธีนี้ใช้ได้กับตัววัตถุเท่านั้นไม่สามารถใช้ได้กับส่วนประกอบย่อย ภายในวัตถุ
เมื่อต้องการจะหาตำแหน่งของส่วนประกอบย่อยมีฟังก์ชันอีกตัวที่ใช้งานได้สะดวกกว่า นั่นคือ xform()
ฟังก์ชันนี้ใช้สำหรับเปลี่ยนค่าหรือหาค่าของวัตถุหรือส่วนประกอบบางอย่างที่ต้องการ ในที่นี้จะใช้เพื่อหาค่าพิกัดของส่วนประกอบที่ต้องการ
กรณีที่ใช้เพื่อหาค่าต้องใส่แฟล็ก q (query) ลงไปเป็น q=1 และใส่แฟล็ก t (translation) จากนั้นฟังก์ชันจะคืนค่าตำแหน่งพิกัดของวัตถุหรือส่วนประกอบเป็นลิส์ของ พิกัดแกน x y z
เช่น
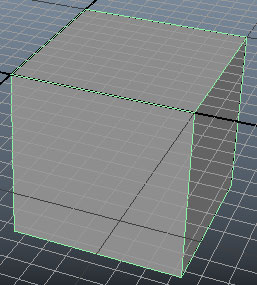
จะได้ค่า [-5,-5,-5]
หรืออาจใช้กับส่วนประกอบ เช่นจุดยอด ก็จะได้ตำแหน่งของจุดยอดนั้น
อย่างไรก็ตาม จะเห็นว่าค่าที่ได้นั้นไม่ใช่ค่าตำแหน่งที่แท้จริงของมัน แต่เป็นตำแหน่งเมื่อเทียบกับใจกลางของวัตถุ
กรณีที่ต้องการหาตำแหน่งสัมบูรณ์เทียบกับฉากหลังจะต้องเพิ่มแฟล็กไปอีกตัว นั่นคือ ws (worldSpace) เป็น ws=1
คราวนี้ลองใช้กับเส้นขอบดู
จะได้ลิสต์ที่มีตัวเลข ๖ ตัว ๓ ตัวแรกคือพิกัด xyz ของจุดยอดจุดหนึ่งที่ประกอบเป็นเส้นขอบนั้น ส่วน ๓ ตัวหลังคือของจุดยอดอีกจุด
หากใช้กับหน้าดู
ก็จะพบว่าได้เป็นลิสต์ที่มีจำนวนสมาชิกเท่ากับ ๓ คูณด้วยจำนวนจุดยอดที่ประกอบเป็นด้านนั้น เช่น ๙ หรือ ๑๒
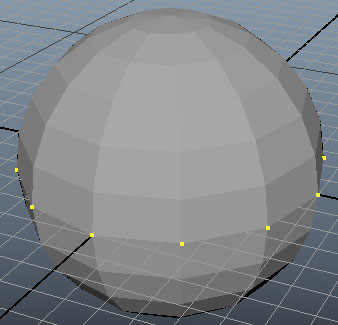
การประยุกต์ใช้งาน เช่นถ้าลองสร้างทรงกลมขึ้นมาอันหนึ่งแล้วต้องการเลือกแค่ส่วน
ในที่นี้ใช้วิธีการให้วนทำซ้ำเพื่อตรวจจุดยอดทีละจุดว่ามีอันไหนมีคุณสมบัติ ตามที่ต้องการ ซึ่งในที่นี้คือต้องการจุดที่มีตำแหน่งในแกน y เป็น 0
อย่างไรก็ตามที่ใส่เป็น abs(t[1])<0.001 แทนที่จะเป็น t[1]==0 เพราะในคอมพิวเตอร์เลขจำนวนจริงที่เห็นว่าเป็นจำนวนง่ายๆอาจไม่ใช่เป็นอย่าง นั้นจริงๆ บางทีอาจมีจุดทศนิยมเป็นจำนวนเล็กๆเช่น 0.000001 อยู่ โดยเฉพาะค่าที่ได้จากการคำนวณบางอย่างมาก่อน
ดังนั้นโดยปกติไม่ควรใช้เครื่องหมาย == กับจำนวนจริงในคอมพิวเตอร์ แต่ใช้วิธีเผื่อขอบเขตบวกลบเล็กน้อยไว้เสมอ ในที่นี้ใช้ 0.001 ก็เพียงพอ
ตอนนี้หากพิมพ์
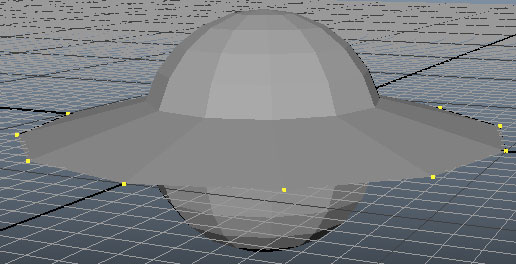
ทรงกลมก็จะแป้นออกกลายเป็นมีหน้าตาคล้ายจานบิน
คราวนี้ลองให้เลือกทั้งหมดที่อยู่ครึ่งบน
แบบนี้จะเห็นว่าเฉพาะส่วนบนถูกเลือก

ตอนนี้ถ้าพิมพ์
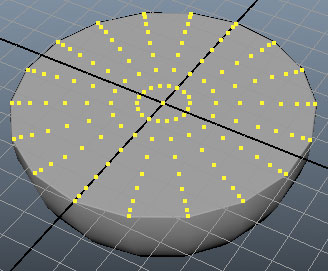
ก็จะออกมาเป็นวัตถุรูปครึ่งวงกลม
ถ้าพิมพ์
ก็จะได้รูปร่างคล้ายๆหลอดทดลอง
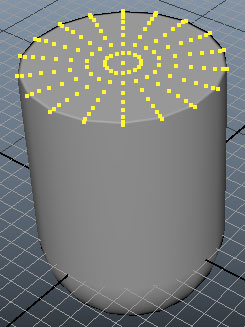
กรณีที่เป้าหมายที่ต้องการเลือกมีอยู่แค่อันเดียวอาจใช้ break ช่วยเพื่อให้หยุดการวนซ้ำทันทีที่เจอเป้าหมาย เครื่องจะได้ไม่ต้องทำงานซ้ำเกินโดยไม่จำเป็น
เช่น คราวนี้ลองสร้างกระโจมโดยหาจุดยอดที่อยู่ตรงกลางด้านบนแล้วดึงสูงขึ้นไป
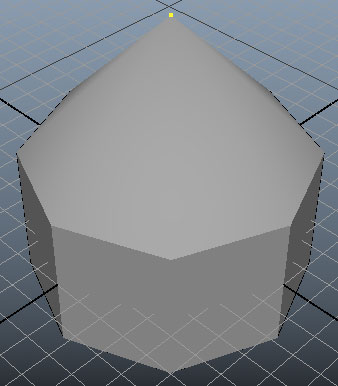
ในตัวอย่างนี้มีการวนซ้ำด้วย for เพื่อหาว่าจุดยอดไหนที่อยู่ด้านบนสุดตรงกลางโดยใช้ xform เพื่อดูข้อมูลตำแหน่ง พอตรวจพบจุดที่อยู่ในตำแหน่งที่ต้องการแล้วจุดนั้นก็จะถูกเลือกและการวนซ้ำ ก็จะสิ้นสุดทันที
นอกจากการหาตำแหน่งเป็นจุดๆด้วยแฟล็ก t แล้ว ยังสามารถหาตำแหน่งที่เป็นขอบเขตของวัตถุหรือเส้นขอบหรือด้านได้ ด้วยการแทนแฟล็ก t ด้วยแฟล็ก bb (boundingBox)
ลอง
จะได้ตัวเลขออกมา ๖ ตัว ๓ ตัวแรกเป็นขอบเขตที่ x y z ต่ำสุด ตามลำดับ และ ๓ ตัวหลังเป็นขอบเขตที่ x y z สูงสุด เมื่อดูค่าเหล่านี้จะทำให้รู้ว่าด้านนี้มีขอบเขตอยู่ในช่วงไหน และอาจนำไปหาตำแหน่งใจกลางหรือความกว้างได้ คือ
bb นั้นอาจใช้ได้ทั้งกับเส้นขอบ ด้าน หรือทั้งตัววัตถุ
ลองใช้วิธีนี้สร้างทรงกลมแล้วคัดเลือกหน้าที่อยู่ครึ่งล่างออกมาแล้วลบ กลายเป็นรูปร่างคล้ายโดมครึ่งทรงกลม

นอกจากจะคัดกรองส่วนประกอบเพื่อเลือกแล้ว เราอาจใช้ xform() เพื่อกำหนดค่าบางอย่างที่ต้องการให้เปลี่ยนไปตามตำแหน่งของวัตถุ
สามารถนำมาใช้ประโยชน์เพื่อวาดกราฟสามมิติได้ เช่น
แบบนี้จะได้ทรงพาราโบลา
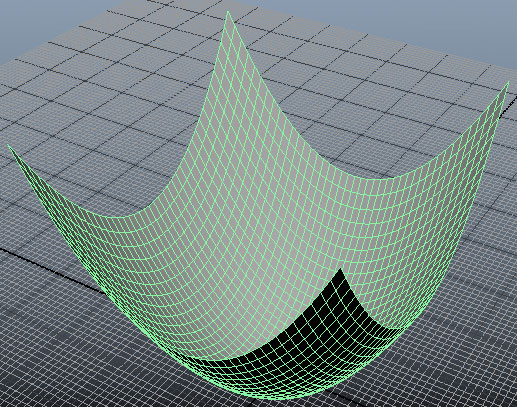
ลองใส่ฟังก์ชันตรีโกณไปให้กลายเป็นผิวรูปคลื่น

ลองประยุกต์ใช้กับทรงกลมก็ได้ เช่น ลองสร้างผลอะไรที่ดูเป็นแฉกๆคล้ายบวบ
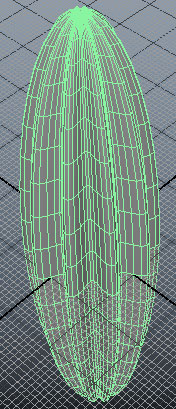
จะเห็นว่าส่วนประกอบแต่ละอันถูกย่อหรือขยายตามแนวนอน (xz) โดยขึ้นอยู่กับลองจิจูด ซึ่งลองจิจูดก็คำนวณมาจาก arctan ของตำแหน่งในแนว x และ z แต่ต้องระวังกรณีที่เป็น 0 ด้วย
หรืออาจทำเป็นหนามๆคล้ายทุเรียนก็ได้

ในที่นี้มีการใช้ละติจูดด้วย ซึ่งก็คำนวณจาก arcsin
จะเห็นว่าสามารถนำไปประยุกต์ใช้อะไรต่างๆได้มากมายเพื่อให้ได้รูปทรงตามที่ต้องการ
อ้างอิง
ตัวเลขของส่วนประกอบเหล่านั้นแม้จะมีหลักตายตัว แต่บางทีก็ไม่ง่ายที่จะทำความเข้าใจได้ ไม่ใช่ว่าสามารถที่จะรู้ได้ตลอด ยิ่งเมื่อสร้างไปเรื่อยๆจะพบจุดยอดมากมาย ยากต่อการคาดเดามากขึ้น
การที่จะเลือกส่วนประกอบที่ต้องการได้โดยไม่จำเป็นต้องรู้หมายเลขนั้นง่าย ที่สุดก็คือการดูจากตำแหน่ง ว่าเราต้องการที่จะเลือกส่วนที่อยู่ตรงไหน
โดยปกติถ้าเป็นวัตถุถ้าหากเราต้องการหาตำแหน่งสามารถใช้ getAttr('.t') ได้ แต่ว่าวิธีนี้ใช้ได้กับตัววัตถุเท่านั้นไม่สามารถใช้ได้กับส่วนประกอบย่อย ภายในวัตถุ
เมื่อต้องการจะหาตำแหน่งของส่วนประกอบย่อยมีฟังก์ชันอีกตัวที่ใช้งานได้สะดวกกว่า นั่นคือ xform()
ฟังก์ชันนี้ใช้สำหรับเปลี่ยนค่าหรือหาค่าของวัตถุหรือส่วนประกอบบางอย่างที่ต้องการ ในที่นี้จะใช้เพื่อหาค่าพิกัดของส่วนประกอบที่ต้องการ
กรณีที่ใช้เพื่อหาค่าต้องใส่แฟล็ก q (query) ลงไปเป็น q=1 และใส่แฟล็ก t (translation) จากนั้นฟังก์ชันจะคืนค่าตำแหน่งพิกัดของวัตถุหรือส่วนประกอบเป็นลิส์ของ พิกัดแกน x y z
เช่น
mc.polyCube(w=10,h=10,d=10)
mc.move(-5,-5,-5)
print(mc.xform(q=1,t=1))
mc.move(-5,-5,-5)
print(mc.xform(q=1,t=1))

จะได้ค่า [-5,-5,-5]
หรืออาจใช้กับส่วนประกอบ เช่นจุดยอด ก็จะได้ตำแหน่งของจุดยอดนั้น
print(xform('.vtx[0]',q=1,t=1))
อย่างไรก็ตาม จะเห็นว่าค่าที่ได้นั้นไม่ใช่ค่าตำแหน่งที่แท้จริงของมัน แต่เป็นตำแหน่งเมื่อเทียบกับใจกลางของวัตถุ
กรณีที่ต้องการหาตำแหน่งสัมบูรณ์เทียบกับฉากหลังจะต้องเพิ่มแฟล็กไปอีกตัว นั่นคือ ws (worldSpace) เป็น ws=1
print(xform('.vtx[0]',q=1,t=1,ws=1))
คราวนี้ลองใช้กับเส้นขอบดู
print(xform('.e[0]',q=1,t=1))
จะได้ลิสต์ที่มีตัวเลข ๖ ตัว ๓ ตัวแรกคือพิกัด xyz ของจุดยอดจุดหนึ่งที่ประกอบเป็นเส้นขอบนั้น ส่วน ๓ ตัวหลังคือของจุดยอดอีกจุด
หากใช้กับหน้าดู
print(xform('.f[0]',q=1,t=1))
ก็จะพบว่าได้เป็นลิสต์ที่มีจำนวนสมาชิกเท่ากับ ๓ คูณด้วยจำนวนจุดยอดที่ประกอบเป็นด้านนั้น เช่น ๙ หรือ ๑๒
การประยุกต์ใช้งาน เช่นถ้าลองสร้างทรงกลมขึ้นมาอันหนึ่งแล้วต้องการเลือกแค่ส่วน
mc.polySphere(r=5,sx=12,sy=12,n='songklom')
mc.select(cl=1)
for i in range(mc.polyEvaluate('songklom',v=1)):
t = mc.xform('songklom.vtx[%d]'%i,t=1,q=1)
if(abs(t[1])<0.001):
mc.select('songklom.vtx[%d]'%i,add=1)
mc.select(cl=1)
for i in range(mc.polyEvaluate('songklom',v=1)):
t = mc.xform('songklom.vtx[%d]'%i,t=1,q=1)
if(abs(t[1])<0.001):
mc.select('songklom.vtx[%d]'%i,add=1)
ในที่นี้ใช้วิธีการให้วนทำซ้ำเพื่อตรวจจุดยอดทีละจุดว่ามีอันไหนมีคุณสมบัติ ตามที่ต้องการ ซึ่งในที่นี้คือต้องการจุดที่มีตำแหน่งในแกน y เป็น 0

อย่างไรก็ตามที่ใส่เป็น abs(t[1])<0.001 แทนที่จะเป็น t[1]==0 เพราะในคอมพิวเตอร์เลขจำนวนจริงที่เห็นว่าเป็นจำนวนง่ายๆอาจไม่ใช่เป็นอย่าง นั้นจริงๆ บางทีอาจมีจุดทศนิยมเป็นจำนวนเล็กๆเช่น 0.000001 อยู่ โดยเฉพาะค่าที่ได้จากการคำนวณบางอย่างมาก่อน
ดังนั้นโดยปกติไม่ควรใช้เครื่องหมาย == กับจำนวนจริงในคอมพิวเตอร์ แต่ใช้วิธีเผื่อขอบเขตบวกลบเล็กน้อยไว้เสมอ ในที่นี้ใช้ 0.001 ก็เพียงพอ
ตอนนี้หากพิมพ์
mc.scale(2,1,2)
ทรงกลมก็จะแป้นออกกลายเป็นมีหน้าตาคล้ายจานบิน

คราวนี้ลองให้เลือกทั้งหมดที่อยู่ครึ่งบน
mc.polySphere(r=5,sx=18,sy=18,n='songklom')
mc.select(cl=1)
for i in range(mc.polyEvaluate('songklom',v=1)):
t = mc.xform('songklom.vtx[%d]'%i,t=1,q=1)
if(t[1]>0.001):
mc.select('songklom.vtx[%d]'%i,add=1)
mc.select(cl=1)
for i in range(mc.polyEvaluate('songklom',v=1)):
t = mc.xform('songklom.vtx[%d]'%i,t=1,q=1)
if(t[1]>0.001):
mc.select('songklom.vtx[%d]'%i,add=1)
แบบนี้จะเห็นว่าเฉพาะส่วนบนถูกเลือก

ตอนนี้ถ้าพิมพ์
mc.scale(1,0,1)
ก็จะออกมาเป็นวัตถุรูปครึ่งวงกลม

ถ้าพิมพ์
mc.move(10,y=1)
ก็จะได้รูปร่างคล้ายๆหลอดทดลอง

กรณีที่เป้าหมายที่ต้องการเลือกมีอยู่แค่อันเดียวอาจใช้ break ช่วยเพื่อให้หยุดการวนซ้ำทันทีที่เจอเป้าหมาย เครื่องจะได้ไม่ต้องทำงานซ้ำเกินโดยไม่จำเป็น
เช่น คราวนี้ลองสร้างกระโจมโดยหาจุดยอดที่อยู่ตรงกลางด้านบนแล้วดึงสูงขึ้นไป
mc.polyCylinder(r=5,h=5,sx=8,sy=1,sz=1,n='krachom')
for i in range(mc.polyEvaluate(v=1)):
t = mc.xform('.vtx[%d]'%i,t=1,q=1)
if(t[0]**2+t[2]**2<0.001 and t[1]>0):
mc.select('.vtx[%d]'%i)
break
mc.move(0,5,0,r=1)
for i in range(mc.polyEvaluate(v=1)):
t = mc.xform('.vtx[%d]'%i,t=1,q=1)
if(t[0]**2+t[2]**2<0.001 and t[1]>0):
mc.select('.vtx[%d]'%i)
break
mc.move(0,5,0,r=1)

ในตัวอย่างนี้มีการวนซ้ำด้วย for เพื่อหาว่าจุดยอดไหนที่อยู่ด้านบนสุดตรงกลางโดยใช้ xform เพื่อดูข้อมูลตำแหน่ง พอตรวจพบจุดที่อยู่ในตำแหน่งที่ต้องการแล้วจุดนั้นก็จะถูกเลือกและการวนซ้ำ ก็จะสิ้นสุดทันที
นอกจากการหาตำแหน่งเป็นจุดๆด้วยแฟล็ก t แล้ว ยังสามารถหาตำแหน่งที่เป็นขอบเขตของวัตถุหรือเส้นขอบหรือด้านได้ ด้วยการแทนแฟล็ก t ด้วยแฟล็ก bb (boundingBox)
ลอง
print(xform('.f[0]',q=1,bb=1))
จะได้ตัวเลขออกมา ๖ ตัว ๓ ตัวแรกเป็นขอบเขตที่ x y z ต่ำสุด ตามลำดับ และ ๓ ตัวหลังเป็นขอบเขตที่ x y z สูงสุด เมื่อดูค่าเหล่านี้จะทำให้รู้ว่าด้านนี้มีขอบเขตอยู่ในช่วงไหน และอาจนำไปหาตำแหน่งใจกลางหรือความกว้างได้ คือ
bb = xform('.f[0]',q=1,bb=1)
(bb[0]+bb[3])/2 จุดกึ่งกลางในแกน x
(bb[1]+bb[4])/2 จุดกึ่งกลางในแกน y
(bb[2]+bb[5])/2 จุดกึ่งกลางในแกน z
bb[3]-bb[0] ความกว้างในแกน x
bb[4]-bb[1] ความกว้างในแกน y
bb[5]-bb[2] ความกว้างในแกน z
(bb[1]+bb[4])/2 จุดกึ่งกลางในแกน y
(bb[2]+bb[5])/2 จุดกึ่งกลางในแกน z
bb[3]-bb[0] ความกว้างในแกน x
bb[4]-bb[1] ความกว้างในแกน y
bb[5]-bb[2] ความกว้างในแกน z
bb นั้นอาจใช้ได้ทั้งกับเส้นขอบ ด้าน หรือทั้งตัววัตถุ
ลองใช้วิธีนี้สร้างทรงกลมแล้วคัดเลือกหน้าที่อยู่ครึ่งล่างออกมาแล้วลบ กลายเป็นรูปร่างคล้ายโดมครึ่งทรงกลม
mc.polySphere(r=5,sx=18,sy=18,n='khruengsongklom')
mc.select(cl=1)
for i in range(mc.polyEvaluate('khruengsongklom',f=1)):
bb = mc.xform('khruengsongklom.f[%d]'%i,t=1,q=1)
if(bb[4]<-0.001):
mc.select('khruengsongklom.f[%d]'%i,add=1)
mc.delete()
mc.select(cl=1)
for i in range(mc.polyEvaluate('khruengsongklom',f=1)):
bb = mc.xform('khruengsongklom.f[%d]'%i,t=1,q=1)
if(bb[4]<-0.001):
mc.select('khruengsongklom.f[%d]'%i,add=1)
mc.delete()

นอกจากจะคัดกรองส่วนประกอบเพื่อเลือกแล้ว เราอาจใช้ xform() เพื่อกำหนดค่าบางอย่างที่ต้องการให้เปลี่ยนไปตามตำแหน่งของวัตถุ
สามารถนำมาใช้ประโยชน์เพื่อวาดกราฟสามมิติได้ เช่น
mc.polyPlane(w=40,h=40,sx=40,sy=40)
for i in range(mc.polyEvaluate(v=1)):
t = mc.xform('.vtx[%d]'%i,t=1,q=1)
mc.move((t[0]**2+t[2]**2)/20,'.vtx[%d]'%i,y=1)
for i in range(mc.polyEvaluate(v=1)):
t = mc.xform('.vtx[%d]'%i,t=1,q=1)
mc.move((t[0]**2+t[2]**2)/20,'.vtx[%d]'%i,y=1)
แบบนี้จะได้ทรงพาราโบลา

ลองใส่ฟังก์ชันตรีโกณไปให้กลายเป็นผิวรูปคลื่น
import math
mc.polyPlane(w=40,h=40,sx=40,sy=40)
for i in range(mc.polyEvaluate(v=1)):
t = mc.xform('.vtx[%d]'%i,t=1,q=1)
mc.move(math.sin(0.2*math.pi*(t[0]**2+t[2]**2)**0.5)*3,'.vtx[%d]'%i,y=1)
mc.polyPlane(w=40,h=40,sx=40,sy=40)
for i in range(mc.polyEvaluate(v=1)):
t = mc.xform('.vtx[%d]'%i,t=1,q=1)
mc.move(math.sin(0.2*math.pi*(t[0]**2+t[2]**2)**0.5)*3,'.vtx[%d]'%i,y=1)

ลองประยุกต์ใช้กับทรงกลมก็ได้ เช่น ลองสร้างผลอะไรที่ดูเป็นแฉกๆคล้ายบวบ
import math
mc.polySphere(r=10,sx=100,sy=20)
for i in range(mc.polyEvaluate(v=1)):
t = mc.xform('.vtx[%d]'%i,q=1,t=1,ws=1)
if(t[2]!=0): longi = math.atan(t[0]/t[2])
else: longi = 0
w = 1+0.2*math.sin(longi*10)
mc.scale(w,5,w,'.vtx[%d]'%i)
mc.polySphere(r=10,sx=100,sy=20)
for i in range(mc.polyEvaluate(v=1)):
t = mc.xform('.vtx[%d]'%i,q=1,t=1,ws=1)
if(t[2]!=0): longi = math.atan(t[0]/t[2])
else: longi = 0
w = 1+0.2*math.sin(longi*10)
mc.scale(w,5,w,'.vtx[%d]'%i)

จะเห็นว่าส่วนประกอบแต่ละอันถูกย่อหรือขยายตามแนวนอน (xz) โดยขึ้นอยู่กับลองจิจูด ซึ่งลองจิจูดก็คำนวณมาจาก arctan ของตำแหน่งในแนว x และ z แต่ต้องระวังกรณีที่เป็น 0 ด้วย
หรืออาจทำเป็นหนามๆคล้ายทุเรียนก็ได้
import math
mc.polySphere(r=10,sx=40,sy=20,n='thurian')
for i in range(mc.polyEvaluate(v=1)):
t = mc.xform('.vtx[%d]'%i,q=1,t=1,ws=1)
if(t[2]!=0): longi = math.atan(t[0]/t[2])
else: longi = 0
lati = math.asin(t[1]/(t[0]**2+t[1]**2+t[2]**2)**0.5)
w = (1+0.1*math.cos(longi*20))*(1-0.1*math.cos(lati*20))
mc.scale(w,w,w,'.vtx[%d]'%i)
mc.polySphere(r=10,sx=40,sy=20,n='thurian')
for i in range(mc.polyEvaluate(v=1)):
t = mc.xform('.vtx[%d]'%i,q=1,t=1,ws=1)
if(t[2]!=0): longi = math.atan(t[0]/t[2])
else: longi = 0
lati = math.asin(t[1]/(t[0]**2+t[1]**2+t[2]**2)**0.5)
w = (1+0.1*math.cos(longi*20))*(1-0.1*math.cos(lati*20))
mc.scale(w,w,w,'.vtx[%d]'%i)

ในที่นี้มีการใช้ละติจูดด้วย ซึ่งก็คำนวณจาก arcsin
จะเห็นว่าสามารถนำไปประยุกต์ใช้อะไรต่างๆได้มากมายเพื่อให้ได้รูปทรงตามที่ต้องการ
อ้างอิง