maya python เบื้องต้น บทที่ ๓๑: การสร้างเส้นโค้ง NURBS
เขียนเมื่อ 2016/03/11 19:12
แก้ไขล่าสุด 2021/09/28 16:42
ในบทที่ผ่านๆมาเราเล่นแต่กับวัตถุที่เป็นโพลิกอนมาโดยตลอด โพลิกอนนั้นมีข้อดีคือเข้าใจง่าย จึงนิยมใช้ในงานต่างๆมากที่สุด อย่างไรก็ตามวัตถุที่ใช้โพลิกอนมีความเหลี่ยมอยู่เสมอ และเพื่อจะทำให้ดูโค้งมนจะต้องเพิ่มความละเอียดมากขึ้น
ในบทนี้จะลองมาพูดถึงวัตถุอีกชนิดหนึ่งที่มีลักษณะสำคัญเช่นควบคุมส่วนโค้งเว้าได้สะดวกกว่า คือสิ่งที่เรียกว่า NURBS
NURBS เป็นคำย่อ ย่อมาจาก Non-Uniform Rational Basis Spline เป็นระบบหนึ่งในการสร้างวัตถุภายในงานกราฟิกต่างๆ นิยมใช้กันมากในหลายๆโปรแกรม
NURBS จะก่อตัวเป็นเส้นโค้ง (曲線, curve) และเส้นโค้งหลายเส้นจะประกอบกันต่อเกิดเป็นพื้นผิวโค้ง (曲面, surface) ในบทนี้จะพูดถึงเส้นโค้งก่อน
รูปร่างของ NURBS จะถูกควบคุมด้วยสิ่งที่เรียกว่าจุดยอดควบคุม (制御頂点, control vertex) หรือเรียกย่อๆว่า cv เป็นจุดที่กำกับรูปร่างของเส้นโค้ง โดยเส้นโค้งจะลากไปมาระหว่าง cv แต่ละจุดเรียงตามลำดับ
แต่ ว่า cv ไม่ใช่จุดบนเส้นโค้ง แต่เป็นจุดที่อยู่นอกเส้นโค้งแล้วคอยกำกับเส้นโค้งอีกที ดังนั้นการจะสร้างเส้นโค้งขึ้นจาก cv นั้นจึงอาจไม่สะดวกเท่าไหร่นัก จึงมีอีกสิ่งหนึ่งที่อาจถูกใช้งานแทนเพื่อความสะดวก นั่นคือ อีดิตพอยนต์ (エディット ポイント, edit point) เรียกย่อๆว่า ep
ep นั้นคือจุดบนเส้นโค้ง โดยทั่วไปแล้วการสร้างเส้นโค้งในมายาจะสร้างจากการกำหนด ep เป็นหลักเพราะเข้าใจง่ายกว่า cv เพียงแต่ว่าในความเป็นจริงแล้วตำแหน่งของ ep นั้นเป็นเพียงสิ่งที่ได้จากการคำนวณจาก cv ดังนั้นถ้าเราสร้างเส้นโค้งด้วยการกำหนด ep โปรแกรมก็จะไปคำนวณย้อนเพื่อหาค่าจุด cv ที่ทำให้ได้ ep ตามที่เรากำหนดนี้อีกที
ดังนั้นในแง่ของประสิทธิภาพการคำนวณแล้วใช้ cv จะง่ายกว่า ep อย่างไรก็ตามสำหรับผู้ใช้ทั่วๆไป ep จะอำนวยความสะดวกในการใช้มากกว่า
เพื่อให้เห็นภาพความต่างระหว่าง cv กับ ep ชัดเจน เรามาลองสร้างเส้นโค้งขึ้นมาดูกันเลย
การสร้างเส้นโค้งโดยใช้โค้ดไพธอนนั้นสามารถทำได้โดยฟังก์ชัน curve() และใส่พิกัดจุด cv หรือ ep เข้าไปในแฟล็ก
หากจะสร้างด้วยจุด cv ให้ใส่แฟล็ก p (point) และหากจะสร้างด้วยจุด ep ให้ใส่แฟล็ก ep (editPoint)
พิกัดจุดใส่ในลักษณะเป็นลิสต์ของลิสต์ [[x1,y1,z1,],[x2,y2,z2,],[x3,y3,z3,],...]
และเช่นเดียวกับการสร้างโพลิกอน การสร้างเส้นโค้ง NURBS ก็สามารถใส่แฟล็ก n (name) เพื่อตั้งชื่อให้กับวัตถุเส้นโค้งที่จะสร้างขึ้นด้วย
ลองพิมพ์
จะได้เส้นโค้งที่เป็นลักษณะรูปคลื่นมา ๒ อัน แต่ขนาดไม่เท่ากัน ทั้งสองเส้นใช้พิกัดค่าเดียวกันในการสร้าง แต่ว่าเส้นแรกใช้เป็น cv ในขณะที่อีกเส้นใช้เป็น ep
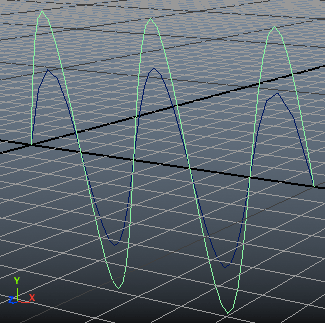
จะเห็นว่าอันที่ใช้เป็น ep นั้นเส้นที่ได้จะลากผ่านจุดพิกัดทุกจุดที่ใส่เข้าไป
ส่วนอันที่ใช้เป็น cv นั้นเส้นจะเลื้อยแคบกว่าพิกัดที่ใส่เข้าไป เพราะว่า cv เป็นแค่จุดกำกับซึ่งจะอยู่ด้านนอกเส้น
จะเห็นว่าแค่ใส่จุดพิกัดลงไปโปรแกรมก็จะทำการสร้างเส้นโค้งออกมาให้โดยอัตโนมัติแทนที่จะเป็นแค่เส้นตรงง่ายๆที่ลากระหว่างจุดแต่ละจุด
นั่นเพราะเส้นเหล่านี้ถูกสร้างขึ้นจากการคำนวณพหุนามโดยใช้จุดหลายจุด ซึ่งจำนวนของจุดที่ใช้นั้นสัมพันธ์กับดีกรีของพหุนาม
ถ้า ดีกรีเป็น 1 จะได้เส้นตรง ซึ่งตำแหน่งของจุดภายในเส้นก็จะถูกคำนวณจากจุดที่กำหนดให้ ๒ จุด แต่ถ้าดีกรีเป็น 2 ก็จะคำนวณโดยใช้จุด ๓ จุด และกลายเป็นเส้นโค้งพาราโบลา
โดยทั่วไปเส้นโค้งในโปรแกรมจะใช้เส้นโค้งดีกรี 3 นั่นคือคำนวณจากจุด ๔ จุด อย่างไรก็ตามหากต้องการดีกรีที่ต่างออกไปก็สามารถกำหนดได้ตอนที่สร้างเส้น โค้งขึ้น โดยใส่แฟล็กเพิ่มอีกตัว คือ d (degree)
ลองสร้างเส้นโค้งที่มีดีกรีต่างๆกันมาเปรียบเทียบกันดู
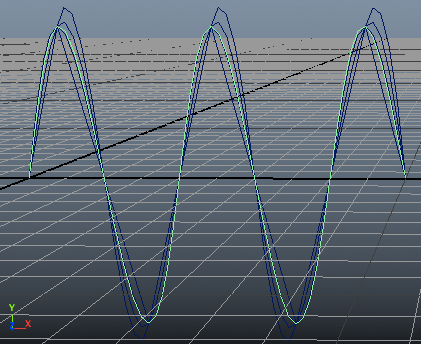
จะเห็นว่าแต่ละเส้นมีความแตกต่างกัน แม้จะมีจุด ep เหมือนกันก็ตาม ความแตกต่างจะเห็นได้จากบริเวณรอยต่อระหว่างจุด ep
ถ้าดีกรี 1 เส้นจะมีความต่อเนื่อง แต่มุมเส้นสัมผัสจะไม่ต่อเนื่อง คือจะเห็นการหักมุม
ถ้าดีกรี 2 เส้นสัมผัสจะมีความต่อเนื่อง แต่ความโค้งจะไม่ต่อเนื่อง คือถึงแม้จะเห็นกราฟไม่มีการหักมุม แต่หากเทียบว่าเป็นเส้นของการเคลื่อนที่จะรู้สึกว่าตรงจุดเปลี่ยนนั้นมีการ เปลี่ยนแปลงความเร็วกะทันหัน คือความเร็วไม่ต่อเนื่อง ดูไม่เป็นธรรมชาติ
ถ้าดีกรี 3 ความโค้งจะมีความต่อเนื่อง จะรู้สึกว่าที่จุดเปลี่ยนไม่ได้มีการเปลี่ยนแปลงความเร็วกะทันหัน ดูแล้วเป็นธรรมชาติ
ดังนั้นโดยทั่วไปดีกรี 3 ถือว่าเพียงพอ และนิยมใช้มากที่สุด ปกติยิ่งดีกรีสูงการคำนวณก็จะมีความละเอียดซับซ้อนมากขึ้น จะมีการใช้ดีกรีที่สูงขึ้นไปกว่า 3 ในบางกรณีเท่านั้น
หากต้องการเพิ่มจุดต่อจากเส้นโค้งที่มีอยู่แล้วก็สามารถทำได้ด้วยฟังก์ชัน curve() เช่นกัน โดยใส่อาร์กิวเมนต์ลงไปเป็นชื่อของวัตถุที่ต้องการเพิ่ม แล้วใส่แฟล็ก a (append) เพิ่มลงไปเป็น a=1
เช่น ลองใช้ลิสต์เดิมสร้างเส้นโค้งโดยคราวนี้เริ่มสร้างจากจุดเดียวแล้วเพิ่ม cv ไปทีละจุด
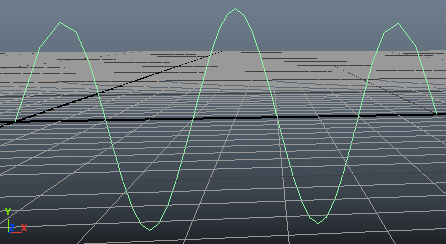
จะเห็นว่าได้ผลเหมือนกับใส่จุดทั้งหมดไปทีเดียวตอนสร้างเส้น
เรา สามารถเข้าถึงโครงสร้างภายในเส้นโค้งได้โดยวิธีคล้ายกับโพลิกอน คืออ้างอิงโดยใช้ชื่อของวัตถุตามด้วยจุดแล้วก็ชนิดขององค์ประกอบ ตามด้วยหมายเลข
สำหรับ cv คือ 'ชื่อวัตถุ.cv[หมายเลข]'
สำหรับ ep คือ 'ชื่อวัตถุ.ep[หมายเลข]'
ลองพิมพ์
จะเป็นการสร้างเส้นกราฟแบบเดียวกับตัวอย่างก่อนหน้า โดยสร้างเสร็จก็กดเลือกจุด cv หมายเลข 6

เราสามารถทำการลบจุด cv ออกได้ด้วย delete() เช่น
แบบนี้จุด cv[6] ก็จะถูกลบออกไป เส้นก็จะมีรูปร่างเปลี่ยนไปเพราะไม่มีจุดตรงนั้นแล้ว และจุดที่เคยเป็น cv[7] ก็จะกลายเป็น cv[6] แทน
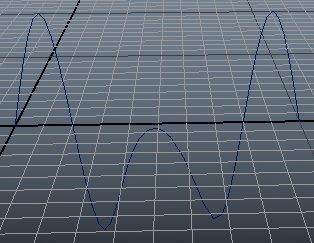
หากจะเข้าถึง cv ทั้งหมดก็ใช้ *
ep เองก็สามารถเข้าถึงได้ในลักษณะเดียวกัน เช่นลองย้าย ep
สามารถใช้ getAttr() เพื่อดูค่าตำแหน่งขององค์ประกอบได้ หากใช้ getAttr('.ep[หมายเลข]') หรือ getAttr('.cv[หมายเลข]') จะได้ผลออกมาเป็นลิสต์ของทูเพิล โดยทูเพิลที่อยู่ภายในลิสต์นั้นเป็นพิกัด xyz ของจุด ep หรือ cv นั้น
เช่น
จะได้พิกัดของ ep และ cv ทั้งหมดของเส้นโค้งที่สร้างขึ้นมา
จะเห็นว่ามีการใส่ [0] ลงไปตรงท้าย เนื่องจากว่าค่าที่คืคกลับมาไม่ใช่แค่ทูเพิลหรือลิสต์เฉยๆ แต่เป็นลิสต์ของทูเพิล จึงต้องใส่ [0] เพื่อให้เข้าถึงทูเพิลซึ่งอยู่ภายในลิสต์
สำหรับ mc.getAttr('sen.ep[%d]'%i) นั้นจะได้ลิสต์ที่ประกอบดูทูเพิลเพียงตัวเดียว จึงมีแต่ [0] แต่สำหรับ mc.getAttr('sen.ep[*]') จะได้ลิสต์ที่มีทูเพิลหลายตัว จำนวนเท่ากับจำนวน ep ทั้งหมดที่มี
นอกจากนี้ยังสามารถใช้ setAttr() เพื่อเปลี่ยนตำแหน่งของ cv แต่ละจุดได้ด้วย แต่สำหรับ ep ไม่สามารถทำอะไรได้
cv นั้นยังสามารถใช้ setKeyframe() หรือ expression() เพื่อทำเป็นภาพเคลื่อนไหวได้ด้วย
เช่น
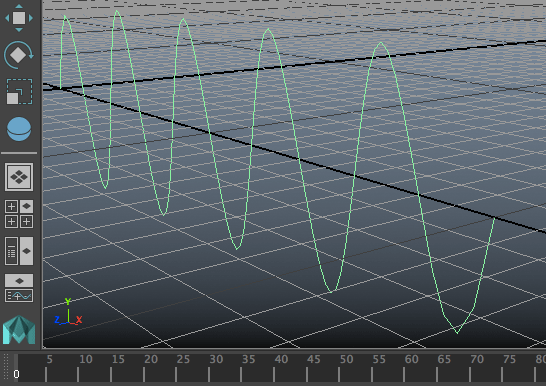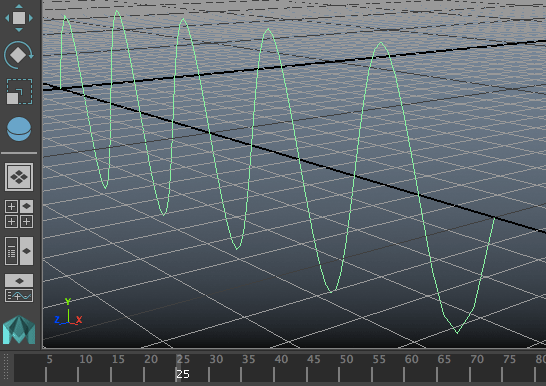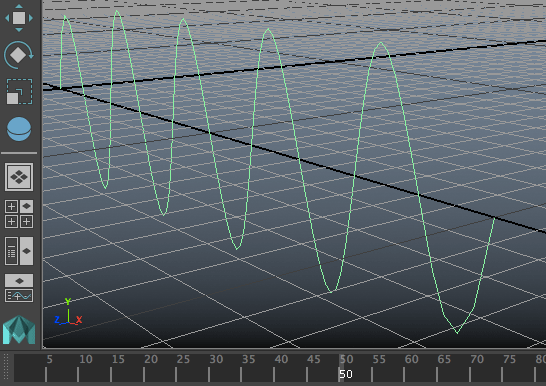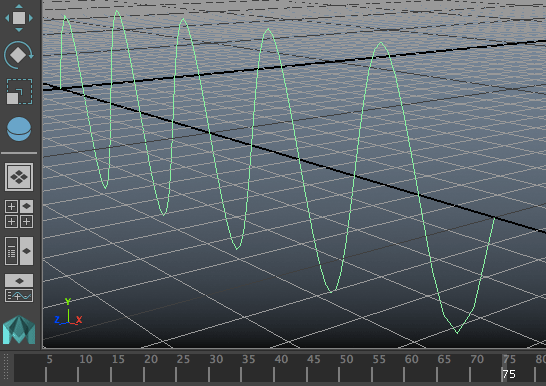
จะได้คลื่นในเส้นเชือกที่ปลายสองข้างถูกตรึง
สำหรับเส้นโค้งที่เป็นวงนั้นสามารถสร้างได้ง่ายๆด้วยฟังก์ชัน circle()
แฟล็กหลักๆของฟังก์ชัน circle() นี้มีดังนี้
ตัวอย่าง

จะเห็นว่าสามารถเข้าถึงจุด ep และ cv เพื่อเลื่อนตำแหน่งหรือทำอะไรได้เหมือนกับในเส้นโค้งจาก curve()
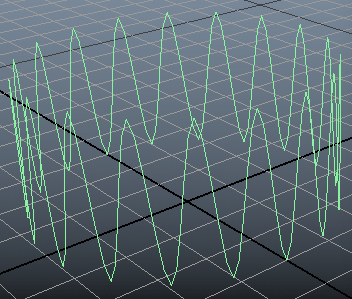
ลองยกจุด ep ขึ้นแบบสลับจุดเว้นจุด เลื่อนเฉพาะจุดที่เป็นเลขคู่ แบบนี้ก็จะได้วงกลมหยึกหยักเป็นคลื่น
เท่านี้ก็สามารถสร้างเส้น NURBS แบบต่างๆได้มากมายแล้ว เพียงแต่ว่าเส้นที่สร้างขึ้นมาตอนนี้ยังไม่ได้นำไปใช้ประโยชน์อะไร สำหรับการใช้ประโยชน์ที่เห็นชัดจะแนะนำในบทที่ ๓๓
อ้างอิง
ในบทนี้จะลองมาพูดถึงวัตถุอีกชนิดหนึ่งที่มีลักษณะสำคัญเช่นควบคุมส่วนโค้งเว้าได้สะดวกกว่า คือสิ่งที่เรียกว่า NURBS
NURBS เป็นคำย่อ ย่อมาจาก Non-Uniform Rational Basis Spline เป็นระบบหนึ่งในการสร้างวัตถุภายในงานกราฟิกต่างๆ นิยมใช้กันมากในหลายๆโปรแกรม
NURBS จะก่อตัวเป็นเส้นโค้ง (曲線, curve) และเส้นโค้งหลายเส้นจะประกอบกันต่อเกิดเป็นพื้นผิวโค้ง (曲面, surface) ในบทนี้จะพูดถึงเส้นโค้งก่อน
รูปร่างของ NURBS จะถูกควบคุมด้วยสิ่งที่เรียกว่าจุดยอดควบคุม (制御頂点, control vertex) หรือเรียกย่อๆว่า cv เป็นจุดที่กำกับรูปร่างของเส้นโค้ง โดยเส้นโค้งจะลากไปมาระหว่าง cv แต่ละจุดเรียงตามลำดับ
แต่ ว่า cv ไม่ใช่จุดบนเส้นโค้ง แต่เป็นจุดที่อยู่นอกเส้นโค้งแล้วคอยกำกับเส้นโค้งอีกที ดังนั้นการจะสร้างเส้นโค้งขึ้นจาก cv นั้นจึงอาจไม่สะดวกเท่าไหร่นัก จึงมีอีกสิ่งหนึ่งที่อาจถูกใช้งานแทนเพื่อความสะดวก นั่นคือ อีดิตพอยนต์ (エディット ポイント, edit point) เรียกย่อๆว่า ep
ep นั้นคือจุดบนเส้นโค้ง โดยทั่วไปแล้วการสร้างเส้นโค้งในมายาจะสร้างจากการกำหนด ep เป็นหลักเพราะเข้าใจง่ายกว่า cv เพียงแต่ว่าในความเป็นจริงแล้วตำแหน่งของ ep นั้นเป็นเพียงสิ่งที่ได้จากการคำนวณจาก cv ดังนั้นถ้าเราสร้างเส้นโค้งด้วยการกำหนด ep โปรแกรมก็จะไปคำนวณย้อนเพื่อหาค่าจุด cv ที่ทำให้ได้ ep ตามที่เรากำหนดนี้อีกที
ดังนั้นในแง่ของประสิทธิภาพการคำนวณแล้วใช้ cv จะง่ายกว่า ep อย่างไรก็ตามสำหรับผู้ใช้ทั่วๆไป ep จะอำนวยความสะดวกในการใช้มากกว่า
เพื่อให้เห็นภาพความต่างระหว่าง cv กับ ep ชัดเจน เรามาลองสร้างเส้นโค้งขึ้นมาดูกันเลย
การสร้างเส้นโค้งโดยใช้โค้ดไพธอนนั้นสามารถทำได้โดยฟังก์ชัน curve() และใส่พิกัดจุด cv หรือ ep เข้าไปในแฟล็ก
หากจะสร้างด้วยจุด cv ให้ใส่แฟล็ก p (point) และหากจะสร้างด้วยจุด ep ให้ใส่แฟล็ก ep (editPoint)
พิกัดจุดใส่ในลักษณะเป็นลิสต์ของลิสต์ [[x1,y1,z1,],[x2,y2,z2,],[x3,y3,z3,],...]
และเช่นเดียวกับการสร้างโพลิกอน การสร้างเส้นโค้ง NURBS ก็สามารถใส่แฟล็ก n (name) เพื่อตั้งชื่อให้กับวัตถุเส้นโค้งที่จะสร้างขึ้นด้วย
ลองพิมพ์
chut = [[0,0,0],[1,4,0],[2,0,0],[3,-4,0],[4,0,0],[5,4,0],[6,0,0],[7,-4,0],[8,0,0],[9,4,0],[10,0,0]]
mc.curve(p=chut,n='chai_cv')
mc.curve(ep=chut,n='chai_ep')
mc.curve(p=chut,n='chai_cv')
mc.curve(ep=chut,n='chai_ep')
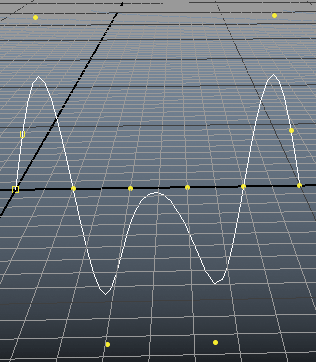
จะได้เส้นโค้งที่เป็นลักษณะรูปคลื่นมา ๒ อัน แต่ขนาดไม่เท่ากัน ทั้งสองเส้นใช้พิกัดค่าเดียวกันในการสร้าง แต่ว่าเส้นแรกใช้เป็น cv ในขณะที่อีกเส้นใช้เป็น ep

จะเห็นว่าอันที่ใช้เป็น ep นั้นเส้นที่ได้จะลากผ่านจุดพิกัดทุกจุดที่ใส่เข้าไป
ส่วนอันที่ใช้เป็น cv นั้นเส้นจะเลื้อยแคบกว่าพิกัดที่ใส่เข้าไป เพราะว่า cv เป็นแค่จุดกำกับซึ่งจะอยู่ด้านนอกเส้น
จะเห็นว่าแค่ใส่จุดพิกัดลงไปโปรแกรมก็จะทำการสร้างเส้นโค้งออกมาให้โดยอัตโนมัติแทนที่จะเป็นแค่เส้นตรงง่ายๆที่ลากระหว่างจุดแต่ละจุด
นั่นเพราะเส้นเหล่านี้ถูกสร้างขึ้นจากการคำนวณพหุนามโดยใช้จุดหลายจุด ซึ่งจำนวนของจุดที่ใช้นั้นสัมพันธ์กับดีกรีของพหุนาม
ถ้า ดีกรีเป็น 1 จะได้เส้นตรง ซึ่งตำแหน่งของจุดภายในเส้นก็จะถูกคำนวณจากจุดที่กำหนดให้ ๒ จุด แต่ถ้าดีกรีเป็น 2 ก็จะคำนวณโดยใช้จุด ๓ จุด และกลายเป็นเส้นโค้งพาราโบลา
โดยทั่วไปเส้นโค้งในโปรแกรมจะใช้เส้นโค้งดีกรี 3 นั่นคือคำนวณจากจุด ๔ จุด อย่างไรก็ตามหากต้องการดีกรีที่ต่างออกไปก็สามารถกำหนดได้ตอนที่สร้างเส้น โค้งขึ้น โดยใส่แฟล็กเพิ่มอีกตัว คือ d (degree)
ลองสร้างเส้นโค้งที่มีดีกรีต่างๆกันมาเปรียบเทียบกันดู
import math
chut = [[x,4*math.sin(x*math.pi/2),0] for x in range(11)]
for i in range(1,6):
mc.curve(ep=chut,d=i,n='degree%d'%i)
chut = [[x,4*math.sin(x*math.pi/2),0] for x in range(11)]
for i in range(1,6):
mc.curve(ep=chut,d=i,n='degree%d'%i)

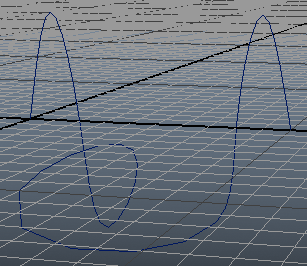
จะเห็นว่าแต่ละเส้นมีความแตกต่างกัน แม้จะมีจุด ep เหมือนกันก็ตาม ความแตกต่างจะเห็นได้จากบริเวณรอยต่อระหว่างจุด ep
ถ้าดีกรี 1 เส้นจะมีความต่อเนื่อง แต่มุมเส้นสัมผัสจะไม่ต่อเนื่อง คือจะเห็นการหักมุม
ถ้าดีกรี 2 เส้นสัมผัสจะมีความต่อเนื่อง แต่ความโค้งจะไม่ต่อเนื่อง คือถึงแม้จะเห็นกราฟไม่มีการหักมุม แต่หากเทียบว่าเป็นเส้นของการเคลื่อนที่จะรู้สึกว่าตรงจุดเปลี่ยนนั้นมีการ เปลี่ยนแปลงความเร็วกะทันหัน คือความเร็วไม่ต่อเนื่อง ดูไม่เป็นธรรมชาติ
ถ้าดีกรี 3 ความโค้งจะมีความต่อเนื่อง จะรู้สึกว่าที่จุดเปลี่ยนไม่ได้มีการเปลี่ยนแปลงความเร็วกะทันหัน ดูแล้วเป็นธรรมชาติ
ดังนั้นโดยทั่วไปดีกรี 3 ถือว่าเพียงพอ และนิยมใช้มากที่สุด ปกติยิ่งดีกรีสูงการคำนวณก็จะมีความละเอียดซับซ้อนมากขึ้น จะมีการใช้ดีกรีที่สูงขึ้นไปกว่า 3 ในบางกรณีเท่านั้น
หากต้องการเพิ่มจุดต่อจากเส้นโค้งที่มีอยู่แล้วก็สามารถทำได้ด้วยฟังก์ชัน curve() เช่นกัน โดยใส่อาร์กิวเมนต์ลงไปเป็นชื่อของวัตถุที่ต้องการเพิ่ม แล้วใส่แฟล็ก a (append) เพิ่มลงไปเป็น a=1
เช่น ลองใช้ลิสต์เดิมสร้างเส้นโค้งโดยคราวนี้เริ่มสร้างจากจุดเดียวแล้วเพิ่ม cv ไปทีละจุด
import math
chut = [[x,4*math.sin(x*math.pi/2),0] for x in range(11)]
mc.curve(p=chut[0],n='sen')
for i in range(1,11):
mc.curve('sen',p=chut[i],a=1)
chut = [[x,4*math.sin(x*math.pi/2),0] for x in range(11)]
mc.curve(p=chut[0],n='sen')
for i in range(1,11):
mc.curve('sen',p=chut[i],a=1)

จะเห็นว่าได้ผลเหมือนกับใส่จุดทั้งหมดไปทีเดียวตอนสร้างเส้น
เรา สามารถเข้าถึงโครงสร้างภายในเส้นโค้งได้โดยวิธีคล้ายกับโพลิกอน คืออ้างอิงโดยใช้ชื่อของวัตถุตามด้วยจุดแล้วก็ชนิดขององค์ประกอบ ตามด้วยหมายเลข
สำหรับ cv คือ 'ชื่อวัตถุ.cv[หมายเลข]'
สำหรับ ep คือ 'ชื่อวัตถุ.ep[หมายเลข]'
ลองพิมพ์
import math
chut = [[x,4*math.sin(x*math.pi/2),0] for x in range(11)]
mc.curve(ep=chut,n='sen')
mc.select('sen.cv[6]')
chut = [[x,4*math.sin(x*math.pi/2),0] for x in range(11)]
mc.curve(ep=chut,n='sen')
mc.select('sen.cv[6]')
จะเป็นการสร้างเส้นกราฟแบบเดียวกับตัวอย่างก่อนหน้า โดยสร้างเสร็จก็กดเลือกจุด cv หมายเลข 6

เราสามารถทำการลบจุด cv ออกได้ด้วย delete() เช่น
mc.delete('sen.cv[6]')
แบบนี้จุด cv[6] ก็จะถูกลบออกไป เส้นก็จะมีรูปร่างเปลี่ยนไปเพราะไม่มีจุดตรงนั้นแล้ว และจุดที่เคยเป็น cv[7] ก็จะกลายเป็น cv[6] แทน

หากจะเข้าถึง cv ทั้งหมดก็ใช้ *
mc.select('sen.cv[*]')

ep เองก็สามารถเข้าถึงได้ในลักษณะเดียวกัน เช่นลองย้าย ep
mc.move(5,0,10,'sen.ep[5]')

สามารถใช้ getAttr() เพื่อดูค่าตำแหน่งขององค์ประกอบได้ หากใช้ getAttr('.ep[หมายเลข]') หรือ getAttr('.cv[หมายเลข]') จะได้ผลออกมาเป็นลิสต์ของทูเพิล โดยทูเพิลที่อยู่ภายในลิสต์นั้นเป็นพิกัด xyz ของจุด ep หรือ cv นั้น
เช่น
chut = [[x,4*math.sin(x*math.pi/2),0] for x in range(11)]
mc.curve(ep=chut,n='sen')
for i in range(len(mc.getAttr('sen.ep[*]'))):
print('ep%d: %s'%(i,mc.getAttr('sen.ep[%d]'%i)[0]))
for i in range(len(mc.getAttr('sen.cv[*]'))):
print('cv%d: %s'%(i,mc.getAttr('sen.cv[%d]'%i)[0]))
mc.curve(ep=chut,n='sen')
for i in range(len(mc.getAttr('sen.ep[*]'))):
print('ep%d: %s'%(i,mc.getAttr('sen.ep[%d]'%i)[0]))
for i in range(len(mc.getAttr('sen.cv[*]'))):
print('cv%d: %s'%(i,mc.getAttr('sen.cv[%d]'%i)[0]))
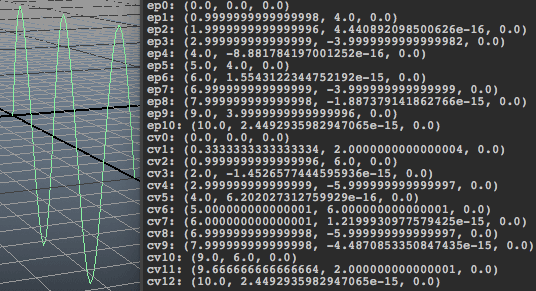
จะได้พิกัดของ ep และ cv ทั้งหมดของเส้นโค้งที่สร้างขึ้นมา

จะเห็นว่ามีการใส่ [0] ลงไปตรงท้าย เนื่องจากว่าค่าที่คืคกลับมาไม่ใช่แค่ทูเพิลหรือลิสต์เฉยๆ แต่เป็นลิสต์ของทูเพิล จึงต้องใส่ [0] เพื่อให้เข้าถึงทูเพิลซึ่งอยู่ภายในลิสต์
สำหรับ mc.getAttr('sen.ep[%d]'%i) นั้นจะได้ลิสต์ที่ประกอบดูทูเพิลเพียงตัวเดียว จึงมีแต่ [0] แต่สำหรับ mc.getAttr('sen.ep[*]') จะได้ลิสต์ที่มีทูเพิลหลายตัว จำนวนเท่ากับจำนวน ep ทั้งหมดที่มี
นอกจากนี้ยังสามารถใช้ setAttr() เพื่อเปลี่ยนตำแหน่งของ cv แต่ละจุดได้ด้วย แต่สำหรับ ep ไม่สามารถทำอะไรได้
cv นั้นยังสามารถใช้ setKeyframe() หรือ expression() เพื่อทำเป็นภาพเคลื่อนไหวได้ด้วย
เช่น
chut = [[x,0,0] for x in range(21)]
mc.curve(p=chut,n='sen')
for i in range(1,len(mc.getAttr('sen.cv[*]'))-1):
mc.expression(o='sen.cv[%d]'%i,s='yv=4*sin((xv+4*time)/2*%f)'%math.pi)
mc.curve(p=chut,n='sen')
for i in range(1,len(mc.getAttr('sen.cv[*]'))-1):
mc.expression(o='sen.cv[%d]'%i,s='yv=4*sin((xv+4*time)/2*%f)'%math.pi)
จะได้คลื่นในเส้นเชือกที่ปลายสองข้างถูกตรึง

สำหรับเส้นโค้งที่เป็นวงนั้นสามารถสร้างได้ง่ายๆด้วยฟังก์ชัน circle()
แฟล็กหลักๆของฟังก์ชัน circle() นี้มีดังนี้
| r | (radius) | รัศมีวงกลม | ค่าตั้งต้นคือ 1 |
| c | (center) | ใจกลางวงกลม | ค่าตั้งต้นคือ [0,0,0] |
| nr | (normal) | แกนหัน | ค่าตั้งต้นคือ [0,0,1] |
| sw | (sweep) | ขนาดมุม | ค่าตั้งต้นคือเต็มวง 360 องศา (2π เรเดียน) |
| d | (degree) | ดีกรี | ค่าตั้งต้นคือ 3 |
| s | (sections) | จำนวน cv | ค่าตั้งต้นคือ 8 |
ตัวอย่าง
mc.circle(r=2,sw=270,c=[1,0,0],nr=[0,1,0],s=16,n='suankhongwongklom')
mc.select('suankhongwongklom.cv[*]')
mc.select('suankhongwongklom.cv[*]')

จะเห็นว่าสามารถเข้าถึงจุด ep และ cv เพื่อเลื่อนตำแหน่งหรือทำอะไรได้เหมือนกับในเส้นโค้งจาก curve()
ลองยกจุด ep ขึ้นแบบสลับจุดเว้นจุด เลื่อนเฉพาะจุดที่เป็นเลขคู่ แบบนี้ก็จะได้วงกลมหยึกหยักเป็นคลื่น
mc.circle(r=3,nr=[0,1,0],s=36,n='wongklomyuekyak')
mc.move(0,3,0,['wongklomyuekyak.ep[%d]'%i for i in range(0,36,2)],r=1)
mc.move(0,3,0,['wongklomyuekyak.ep[%d]'%i for i in range(0,36,2)],r=1)

เท่านี้ก็สามารถสร้างเส้น NURBS แบบต่างๆได้มากมายแล้ว เพียงแต่ว่าเส้นที่สร้างขึ้นมาตอนนี้ยังไม่ได้นำไปใช้ประโยชน์อะไร สำหรับการใช้ประโยชน์ที่เห็นชัดจะแนะนำในบทที่ ๓๓
อ้างอิง
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/curve.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/circle.html
http://help.autodesk.com/view/MAYAUL/2016/JPN/?guid=GUID-5EC05798-3F28-4AD2-8154-36BC444A4DC9
http://www.rhino3d.co.jp/seminar/s_b_0.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/circle.html
http://help.autodesk.com/view/MAYAUL/2016/JPN/?guid=GUID-5EC05798-3F28-4AD2-8154-36BC444A4DC9
http://www.rhino3d.co.jp/seminar/s_b_0.html