[python] วิเคราะห์จำแนกประเภทข้อมูลเป็นสองกลุ่มด้วยการถดถอยโลจิสติก
เขียนเมื่อ 2016/11/03 23:54
แก้ไขล่าสุด 2022/07/21 15:23
ช่วงไม่กี่เดือนที่ผ่านมานี้มีโอกาสได้เริ่มศึกษาเกี่ยวกับเรื่องการเรียนรู้ของเครื่องซึ่งเป็นสาขาที่ช่วงนี้คนกำลังให้ความสนใจอยู่มาก
หลังจากที่ลองซื้อหนังสือมาอ่านๆหลายเล่มอีกทั้งเปิดอ่านตามเว็บต่างๆก็อยากลองเขียนสรุปความรู้ที่ตัวเองได้ลงบล็อกสักหน่อย
เพียงแต่เรื่องนี้เป็นศาสตร์ที่มีรายละเอียดมากมาย หากจะอธิบายตั้งแต่ต้นจริงๆคงต้องรอคนที่เป็นเฉพาะทางมาเขียนมากกว่า (ซึ่งค่อนข้างคาดหวังอยากให้มี เพราะเรื่องนี้ขาดแคลนคนเขียนเป็นภาษาไทยมาก) ในที่นี้คงจะอธิบายละเอียดแค่เท่าที่จะพอทำได้
นี่เป็นบทความแรกที่จะเขียนถึงเรื่องการเรียนรู้ของเครื่อง จากนี้ไปก็ตั้งใจว่าจะเขียนอีกหลายเรื่องต่อไป
เทคนิคการเรียนรู้ของเครื่องมีอยู่หลากหลายรูปแบบมาก แต่ในที่นี้จะเริ่มแนะนำเรื่องของการวิเคราะห์การถดถอยโลจิสติก (逻辑回归, logistic regression) ซึ่งเป็นวิธีการที่นิยมใช้เพื่อจำแนกประเภทข้อมูลหรือสิ่งของบางอย่างออกเป็นสองกลุ่ม
สำหรับเรื่องที่พื้นฐานกว่านั้นเช่นว่า "การวิเคราะห์ถดถอย" คืออะไร มีเขียนเอาไว้ในบทความเรื่อง "การวิเคราะห์การถดถอยเชิงเส้นด้วยการเคลื่อนลงตามความชัน" https://phyblas.hinaboshi.com/20161210 ซึ่งเขียนขึ้นมาทีหลัง แนะนำให้อ่านในนั้นก่อนแล้วค่อยมาอ่านหน้านี้อาจจะดีกว่า
ขอเริ่มจากยกปัญหาโดยลองสมมุติสถานการณ์ง่ายๆ
มีที่ดินอยู่แปลงหนึ่ง ขนาด 40x30 เมตร อยากทดสอบว่าดินบริเวณไหนอุดมสมบูรณ์ก็เลยลองหว่านเมล็ดถั่วไปพันเมล็ดโดยสุ่มตำแหน่ง ผลปรากฏมาตามนี้
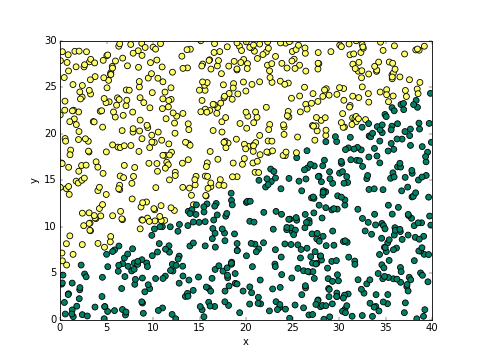
สีเขียวคือต้นถั่วงอก สีเหลืองคือต้นถั่วไม่งอก จะเห็นว่าแบ่งเขตกันชัดเจน ดูด้วยตาก็คงพอกะได้คร่าวๆว่าจะแบ่งเขตยังไงดี
เฉลย... ความจริงแล้วพื้นที่นี้สามารถอธิบายได้ง่ายๆด้วยสมการนี้ นั่นคือเมื่อ x-2y+10>0 ถั่วจะงอก
และภาพนี้ก็ได้มาจากการเขียนโค้ดตามนี้
จะเห็นว่าถ้ารู้สมการแล้วที่เหลือต่อไปนี้เราก็รู้แล้วว่าควรจะปลูกถั่วตรงไหน อย่างไรก็ตามปัญหาก็คือหากเราไม่รู้สมการมาก่อนเราจะทำอย่างไรจึงจะรู้มันได้โดยดูจากแค่ผลของการปลูกถั่วดังในภาพนี้
นั่นล่ะคือหน้าที่ของเทคนิคการวิเคราะห์การถดถอยโลจิสติก
สมมุติว่าถ้าเขตของพื้นที่ถูกแบ่งเป็นเส้นตรงชัดเจนอย่างในตัวอย่างนี้ เราอาจกำหนดฟังก์ชันตัดสินขึ้นมา
..(1)
โดยให้จุดที่ฟังก์ชันตัดสิน f(x,y)=0 เป็นเส้นแบ่งเขต และทำการวิเคราะห์เพื่อหาค่า a, b และ c
ในที่นี้ a กับ b จะถูกเรียกว่าสัมประสิทธิ์น้ำหนัก และ c เรียกว่าเป็นไบแอส
น้ำหนักในที่นี้คนละความหมายกับน้ำหนักตัวของคนหรือสิ่งของ แต่มีความหมายทำนองเดียวกับน้ำหนักเวลาคำนวนค่าทางสถิติ คือหมายถึงความสำคัญหรือสิ่งที่จะบอกว่าค่าข้างหลังมันจะส่งผลถึงค่าของฟังก์ชันมากน้อยแค่ไหน มีผลในทิศทางไหน
ส่วนไบแอสคือค่าศูนย์สำหรับยืนพื้น ในที่นี้เป็นตัวกำหนดว่ากราฟเส้นแบ่งจะเลื่อนไปทางซ้ายขวาบนล่างแค่ไหนโดยไม่เกี่ยวกับความชันเส้นแบ่ง ถ้าไบแอสเป็น 0 กราฟก็จะผ่านจุด 0,0
กรณีตัวอย่างนี้ ผลเฉลยค่า a, b และ c ที่ได้นั้นสุดท้ายควรจะมีความสัมพันธ์ในลักษณะที่เป็น b/a=-2 และ c/a=10
วิธีการที่ใช้กันทั่วไปในการหาค่าเหล่านี้ก็คือ กำหนดค่าเริ่มต้นอะไรก็ได้ไปก่อน แล้วดูว่าผลที่ได้ใกล้เคียงแค่ไหน จากนั้นก็ค่อยๆปรับตัวเลขให้ได้ค่าใกล้เคียงขึ้นไปเรื่อยๆ
การจะดูว่าผลที่ได้นั้นใกล้เคียงแค่ไหน วิธีการง่ายสุดก็คือนับจำนวนที่ทายถูก
เช่น ลองทดสอบโดยเอาข้อมูลผลการปลูกถั่วที่เก็บไว้ในตัวอย่างข้างต้นมาใช้ จากโค้ดที่แล้วข้อมูลถูกเก็บอยู่ใน x_thua, y_thua และ ngokmai เราอาจทำการบันทึกเก็บไว้ก่อนเพื่อนำมาใช้ทีหลัง การบันทึกอาเรย์ทีเดียวหลายตัวเราอาจใช้คำสั่ง np.savez ของ numpy
จากนั้นเราจะดึงไฟล์ .npz ที่บันทึกไว้มาใช้งานได้ด้วยคำสั่ง np.load (รายละเอียดมากกว่านี้อ่านได้ใน numpy เบื้องต้นบทที่ ๓๙)
เช่น ลองสมมุติให้ a=3, b=-15, c=129.3 แล้วลองวาดดูว่าผลเป็นอย่างไร
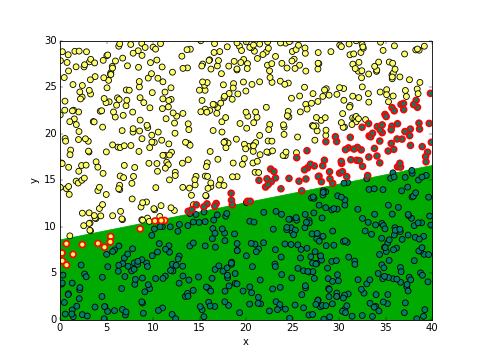
จากรูปนี้บริเวณที่พื้นสีเขียวคือที่ทำนายว่าจะอุดมสมบูรณ์ (จุดเป็นสีเขียว) โดยจุดที่ขอบสีแดงคือที่ทายผิด จะเห็นว่าส่วนใหญ่ทายถูกแล้ว ดังที่จะเห็นได้ว่าค่าที่ print ออกมาได้คือทายถูก 880 จาก 1000
เป้าหมายคือการปรับค่าให้จำนวนที่ผิดมีน้อยลง อย่างไรก็ตาม โดยทั่วไปแล้วแทนที่จะใช้จำนวนที่ทายถูกเป็นเป้าหมายโดยตรง วิธีที่นิยมกว่ากลับเป็นการคำนวณค่าความคลาดเคลื่อนรวม แล้วพยายามปรับให้ความคลาดเคลื่อนรวมน้อยที่สุด
ค่าความคลาดเคลื่อนรวมมักถูกเรียกว่าเป็นค่าเสียหาย (cost หรือ loss) คือเป็นค่าที่จะยิ่งมากขึ้นเมื่อคำนวณหรือทำนายผิด
ค่าเสียหายที่นิยมใช้คือค่าความคลาดเคลื่อนกำลังสองเฉลี่ย (sum of squared error มักย่อว่า SSE) การนำค่าที่ทำนายได้ (ในที่นี้คือ ngokmai) กับค่าจริงๆ (ในที่นี้คือ ngokmang) มาลบกันแล้วยกกำลังสอง จากนั้นก็คิดค่าของทุกจุดแล้วเอามารวมกัน
สามารถคำนวนความคลาดเคลื่อนกำลังสองของแต่ละตัวได้โดย
จะได้ค่าที่เป็น 0 และ 1 สลับกันไป อันที่เป็น 0 คือที่ทายถูก ที่เป็น 1
ดังนั้นแล้วเราสามารถคำนวณ SSE ได้ด้วยการเอาทุกตัวมารวมกัน
อย่างไรก็ตามการที่ให้ทายถูกแล้วเป็น 0 ทายผิดแล้วเป็น 1 แบบนี้เป็นลักษณะของฟังก์ชันขั้นบันได เป็นการแบ่งที่หยาบไปสักหน่อย ในความเป็นจริงที่เรามักจะเจอกันมากกว่าก็คือให้คะแนนความคลาดเคลื่อนในระดับที่ละเอียดกว่านี้
ลองย้อนกลับไปดูตอนแรกที่เราหาค่า ngokmang นั้นเราใช้ a*x_thua+b*y_thua+c มาเทียบว่ามากกว่า 0 หรือเปล่า ถ้ามากกว่าให้เป็น 1 ถ้าน้อยกว่าเป็น 0
แต่คราวนี้แทนที่จะทำอย่างนั้นเราลองเปลี่ยนเป็นว่าถ้ามากกว่า 0 ไปมากๆจึงจะเข้าใกล้ 1 ถ้าน้อยกว่า 0 มากๆให้เข้าใกล้ 0 แต่ถ้าค่าใกล้ๆ 0 ก็ให้มีค่าที่ประมาณ 0.5
ฟังก์ชันที่มีลักษณะเป็นแบบนี้ที่นิยมใช้คือฟังก์ชันซิกมอยด์ (sigmoid)
..(2)
เพื่อให้เห็นภาพลองเอาฟังก์ชันมาเขียนกราฟ เปรียบเทียบกับกราฟแบบขั้นบันไดที่แบ่ง 0 กับ 1 แบบตัดกันชัดเจนแบบเดิมดูด้วย
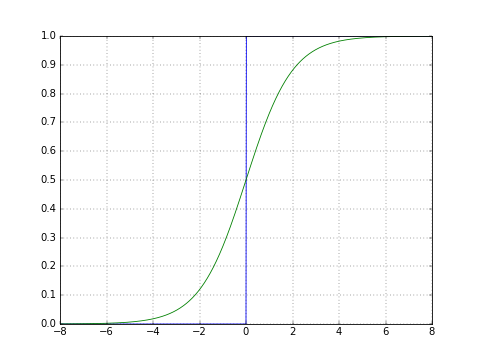
เส้นสีเขียวคือซิกมอยด์ จะเห็นว่ามีการเปลี่ยนแปลงแบบค่อยๆเป็นค่อยๆไป แต่เมื่อมีค่ามากๆก็จะลู่เข้า 1 และเมื่อน้อยมากๆจะลู่เข้า 0
ที่มักใช้แบบนี้เพราะในปัญหาการจำแนกประเภทโดยทั่วไปถ้าฟังก์ชันคำนวณได้ใกล้ 0 แสดงว่าค่าที่คำนวณได้ก็อยู่ใกล้ขอบเขตแบ่งทำให้จริงๆแล้วมันมีโอกาสที่จะอยู่ฝั่งไหนก็ได้ บางทีแทนที่จะตัดสินตูมเดียวไปเลยว่าเป็น 0 หรือ 1 การตัดสินให้ค่าเป็นตัวเลขอยู่ในช่วงระหว่าง 0 ถึง 1 จะดูประนีประนอมกว่า
ในกรณีตัวอย่างนี้ f(x) = ax+bx+c เป็นฟังก์ชันตัดสินของเรา ซึ่งอาจให้ค่าอะไรก็ได้ตั้งแต่ลบอนันต์ถึงอนันต์ ยิ่งค่ามากยิ่งมีโอกาสเป็นดินดีมาก แต่ถ้าค่าใกล้ 0 ก็อาจก้ำกึ่ง
กรณีนี้ฟังก์ชันเป้าหมายที่ผ่านฟังก์ชันซิกมอยด์แล้วสามารถตีความได้ว่าเป็นความน่าจะเป็นที่บริเวณนั้นจะเป็นดินดี ซึ่งแสดงได้ว่าถ้า sigmoid(0)=0.5 หมายความว่าโอกาสเป็นคือ 50:50
ลองวาดแผนภาพไล่สีดูเปรียบเทียบระหว่างสองแบบ
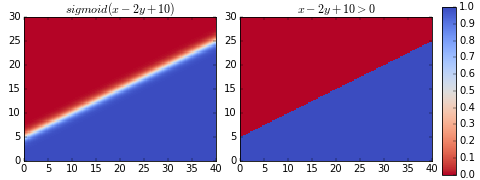
จะสังเกตได้ว่าต่างกันแค่ที่บริเวณใกล้รอยต่อ ซิกมอยด์จะค่อยๆไล่สี ไม่ได้ตัดเปลี่ยนไปทันทีแบบฟังก์ชันขั้นบันได
ซึ่งหมายความว่าถ้าห่างจากรอยต่อมากๆเราจะตัดสินได้ทันทีว่าอยู่กลุ่มไหน แต่ถ้าอยู่แถวๆรอยต่อค่าก็จะก้ำกึ่ง มีความเป็นไปได้ที่จะอยู่กลุ่มไหนก็ได้
ฟังก์ชันซิกมอยด์ในที่นี้เรียกว่าทำหน้าที่เป็นฟังก์ชันกระตุ้น (activation function)
ฟังก์ชันกระตุ้นที่นิยมใช้ยังมีอีกหลากหลายแบบ เช่น relu, tanh, ฯลฯ ซึ่งก็เหมาะใช้ในกรณีต่างกันออกไป
ฟังก์ชันกระตุ้นแบบนี้จะใช้เมื่อตอนคำนวณความควรจะเป็นของค่าที่ทำนายได้เท่านั้น แต่ในผลลัพธ์สุดท้ายแล้วค่าจริงมีเพียง 0 กับ 1 ดังนั้นเมื่อจะเทียบกับค่าจริงว่าทายถูกหรือผิดยังไงก็ต้องมาดูว่าค่ามากหรือน้อยกว่า 0.5 เพื่อแบ่งเป็น 0 หรือ 1
สรุปแล้วสิ่งที่ต้องเปลี่ยนตอนนี้คือ เปลี่ยนค่าทำนายจากเดิมมาเป็น
พอลองดูค่า ngokmang ที่ได้แล้วก็จะพบว่าค่าส่วนใหญ่จะกองกันอยู่ที่ใกล้ 0 และใกล้ 1 แต่ก็จะไม่เป็น 0 หรือ 1 พอดีซะทีเดียว
จากนั้นก็คำนวณค่าเสียหายใหม่อีกที
ค่าเสียหายนี้ตามหนังสือมักแทนด้วยตัว J หากนำค่าเสียหาย SSE เขียนในรูปสมการคณิตศาสตร์จะได้เป็น
..(3)
โดย n คือจำนวนจุดข้อมูลทั้งหมด z(i) คือค่าคำตอบจริงของแต่ละจุด (เป็น 0 หรือ 1) ส่วน φ(i) คือค่าที่คำนวณได้ในแต่ละจุด ในที่นี้มาจากฟังก์ชันซิกมอยด์
..(4)
ในที่นี้เป็นการเขียนในรูปทั่วไป ไม่ได้จำกัดอยู่แค่ ๒ มิติ แต่ให้มี m มิติ ฟังก์ชันตัดสิน f(x(i)) = f(x1,(i),x2,(i),...,xm,(i)) จะเขียนใหม่เป็น
..(5)
wj คือค่าน้ำหนักของตัวแปรต้นแต่ละตัว โดยหากเทียบกับสมการ (1) แล้วในที่นี้เรามีตัวแปรต้น ๓ ตัว แบ่งเป็นน้ำหนักในแกน x ในที่นี้คือ w1=wx=a และน้ำหนักแกน y คือ w2=wy=b ส่วนไบแอส c ในที่นี้เขียนแทนด้วย w0 โดยต่อจากนี้จะเขียน a เป็น wx เขียน b เป็น wy และ c เป็น w0 เพื่อความเข้าใจง่าย
ตอนนี้เราเข้าใจแล้วว่าเป้าหมายคือการเปลี่ยนแปลงค่าน้ำหนักและค่าไบแอสให้ค่า SSE นี้น้อยที่สุด เพื่อการนั้นขั้นต่อไปคือต้องใช้วิธีการที่เรียกว่าการเคลื่อนลงตามความชัน (gradient descent, GD)
***หมายเหตุ ส่วนตรงนี้ต้องใช้ความรู้แคลคูลัสระดับมหาวิทยาลัย ใครไม่สนใจคณิตศาสตร์อาจข้ามไปอ่านส่วนของโค้ดได้เลย
หลักการของวิธีนี้คือหาค่าความชันของฟังก์ชันเทียบกับตัวแปรแต่ละตัว หรือก็คืออนุพันธ์ย่อย จากนั้นปรับเปลี่ยนค่าไปในทางที่ตรงกันข้ามกับความชัน
นั่นคือความเปลี่ยนแปลงของน้ำหนักคำนวณโดย
..(6)
หรือเขียนเป็นภาษาพูดได้ว่า
การเปลี่ยนแปลงค่าน้ำหนัก = -อัตราการเรียนรู้ x ความชันของค่าเสียหายเทียบกับค่าน้ำหนักตัวนั้น
อัตราการเรียนรู้ (η) คือค่าที่จะกำหนดว่าในแต่ละรอบที่คำนวณจะมีการปรับเปลี่ยนค่าน้ำหนักไปมากแค่ไหน
ค่านี้เป็นค่าที่ผู้เขียนโปรแกรมจะต้องกำหนดขึ้นเองให้พอเหมาะ ถ้าหากมากไปค่าจะถูกปรับเยอะไปจนอาจเลยค่าที่เหมาะสมและปรับเท่าไหร่ก็ไม่อาจได้ค่าที่ต้องการได้เลย แต่ถ้าน้อยไปก็จะใช้เวลานานมากกว่าจะลู่เข้าสู่คำตอบที่ต้องการ
ค่าความคลาดเคลื่อนในที่นี้ใช้เป็น SSE แต่ในกรณีอื่นก็อาจใช้อย่างอื่นได้อีก ที่จริงแล้วกรณีปัญหาการถดถอยโลจิสติกมักนิยมใช้ค่าที่เรียกว่าเอนโทรปีไขว้ (cross entropy) มากกว่า แต่ในที่นี้ขอใช้ SSE เนื่องจากเข้าใจง่ายกว่า
ความชันของค่าเสียหาย J ในกรณีที่ J เป็น SSE ดังสมการ (3) เมื่อทำการหาอนุพันธ์ย่อยสำหรับ wj และ w0 ออกมาจะได้เป็น
..(7)
และ
..(8)
ซึ่งสมการ (7) สำหรับ wx และ wy ในตัวอย่างนี้จะได้
..(9)
เมื่อแทนค่าสมการ (8) และ (9) ลงในสมการ (6) ก็จะหาค่าความชันที่ควรเปลี่ยนแปลงไปได้เป็น
..(10)
หากใครไม่สามารถเข้าใจกับคณิตศาสตร์ที่อธิบายมาตรงนี้ก็ขอสรุปสั้นๆแค่ว่าสิ่งที่เราต้องการคือสมการ (10) เพื่อไว้ใช้หาค่าการเปลี่ยนแปลงของความชันและไบแอสในแต่ละรอบ
เมื่ออธิบายทฤษฎีคร่าวๆจนพอรู้แนวทางแล้ว ทีนี้มาลองเขียนโค้ดกันดูเลย
เมื่อรันแล้วก็จะได้ผลออกมาเป็นภาพนี้
ผลที่ได้อาจต่างไปโดยขึ้นกับตำแหน่ง x และ y ของต้นถั่วที่สุ่มมาตอนแรกสุด แต่โดยรวมแล้วแนวโน้มควรจะเหมือนกันคือทายถูกเกือบหมด
สำหรับกรณีของข้อมูลสุ่มชุดนี้ผลที่ได้จะเห็นว่าถูก 994 แสดงว่าผิดแค่ 6 เท่านั้น ดังที่จะเห็นได้ว่ามีจุดขอบแดงอยู่ 6 จุด
สมการที่ได้ก็คือ 0.582x-1.123y+5.066 = 0 ซึ่งก็สอดคล้องกับที่ควรจะเป็นนั่นคือ wy/wx ประมาณ -2 และ w0/wx ประมาณ 10
ค่าความคลาดเคลื่อนรวมและจำนวนที่ทายถูกในแต่ละขั้นได้ถูกเก็บไว้ในตัวแปร sse และ thuktong ลองเอามาวาดกราฟแสดงการเปลี่ยนแปลงของค่า
จะเห็นว่ายิ่งผ่านไปหลายๆรอบความคลาดเคลื่อนรวมยิ่งลดลง และจำนวนครั้งที่ทายถูกก็มากขึ้น
ตอนนี้สามารถเขียนโค้ดสำหรับการเรียนรู้ของเครื่องสำหรับการวิเคราะห์การถดถอยโลจิสติกได้แล้ว แต่อย่างไรก็ตาม เพื่อให้เป็นระบบระเบียบมากขึ้น โดยทั่วไปแล้วการเขียนโดยใช้วิธีการสร้างคลาสจะสะดวกกว่าและเป็นที่นิยมมาก
ลองเขียนใหม่โดยใช้คลาสดูก็จะได้ประมาณนี้
จากนั้นเริ่มการใช้งานโดยสร้างออบเจ็กต์จากคลาส จากนั้นใช้เมธอด rianru เพื่อให้ออบเจ็กต์ทำการเรียนรู้และปรับค่าน้ำหนัก
เสร็จแล้วก็นำมาวาดกราฟผลการเรียนรู้ดู โดยค่าจะเก็บอยู่ในแอตทริบิวต์ sse และ thuktong ของออบเจ็กต์ นำมาใช้ได้เลย
ผลที่ได้จะเหมือนกันกับตอนที่ไม่ใช้คลาส
ค่าน้ำหนักก็อยู่ในแอตทริบิวต์ wx,wy,w0 นำมาแสดงผลได้ในลักษณะเดียวกัน
ในที่นี้ที่ตั้งชื่อคลาสโดยมีคำว่า 2d ต่อท้ายก็เพราะว่าคลาสนี้ใช้กับกรณีที่ตัวแปรต้นมีแค่ ๒ ตัวเท่านั้น อย่างไรก็ตามปัญหาการแบ่งหมวดหมู่โดยทั่วไปอาจมีตัวแปรต้นกี่ตัวก็ได้ ดังนั้นเราลองมาปรับแก้อักสักหน่อยให้ใช้กับกี่ตัวแปรก็ได้
กรณีแบบนี้จะเป็นการสะดวกที่จะใช้ฟังก์ชัน np.dot ซึ่งใช้ในการคูณเมทริกซ์ ซึ่งถ้าใครไม่คุ้นเคยแล้วอาจจะเข้าใจยากขึ้นสักหน่อย แต่หากลองเทียบเคียงกับโค้ดในตัวอย่างบนก็จะเข้าใจง่ายขึ้น
ลองปรับแล้วก็จะออกมาแบบนี้
ในที่นี้ตัวแปร X จะแทนทั้ง x และ y ในโค้ดอันก่อน โดย X ในที่นี้เป็นอาเรย์สองมิติ สามารถสร้างขึ้นจาก x และ y ได้ด้วยฟังก์ชัน np.stack ดังที่เห็น ในตัวอย่างนี้รวมอยู่ในตัวแปรชื่อ xy_thua
พอทำแบบนี้แล้วตัวแปรสำหรับเมธอด rianru ก็จะลดลง แต่ใน X นี้จะแทนตัวแปรต้นกี่ตัวก็ได้ ไม่ใช่ว่าจะมีได้แค่สอง
ส่วน self.w ในที่นี้จะเก็บค่าน้ำหนักทั้งหมด (เทียบเท่า wx และ wy จากโค้ดที่แล้ว) รวมทั้งค่าไบแอส (เทียบเท่ากับ w0 จากโค้ดที่แล้ว) ด้วย พอเขียนรวมกันเป็นตัวแปรเดียวแบบนี้แล้วดูกะทัดรัดขึ้น
ขอส่งท้ายด้วยการทดสอบเกี่ยวกับอัตราการเรียนรู้ (eta) ซึ่งเป็นค่าที่สำคัญที่ต้องกำหนดให้พอเหมาะ
ลองนำคลาสที่เพิ่งสร้างมาใช้โดยปรับค่า eta ให้ต่างๆกันไป แล้ววาดกราฟเพื่อเปรียบเทียบการเรียนรู้ด้วยค่า eta ต่างๆดู
จากผลที่ได้จะเห็นว่าค่า 0.01 กับ 0.001 มากเกินไปจนทำให้ผลที่ได้แกว่งไปมาไม่อาจลู่เข้าสู่ค่าสูงสุดได้
ส่วน 0.00001 ก็น้อยไปทำให้การเปลี่ยนแปลงเป็นไปแบบช้ามาก กว่าจะลู่เข้าได้ก็ต้องทำซ้ำไปอีกนาน
ดังนั้นค่าที่เหมาะที่สุดคือ 0.0001
หากจะเขียนให้ซับซ้อนเพิ่มเติมขึ้นไปอีกแล้วอาจลองทำให้อัตราการเรียนรู้เปลี่ยนแปลงไปตามความเหมาะสม โดยลดลงเรื่อยๆเมื่อทำซ้ำ แบบนี้จะทำให้ช่วงแรกลู่เข้าได้เร็วแล้วช่วงหลังเข้าใกล้ค่าที่ต้องการได้มากที่สุด
สิ่งที่ควรปรับปรุงอีกก็เช่นเปลี่ยนฟังก์ชันค่าเสียหายจาก SSE มาเป็นอย่างอื่นเช่นเอนโทรปีไขว้
ในตัวอย่างทั้งหมดที่เขียนในนี้เป็นแค่พื้นฐานเบื้องต้น ยังมีอะไรๆต้องปรับปรุงอีกมากมายจึงจะเหมาะแก่การใช้งานจริงๆ
ในทางปฏิบัติแล้วปัจจุบันมีมอดูลหลายตัวในไพธอนที่มีฟังก์ชันและคลาสที่สำเร็จรูปเหมาะสำหรับการเรียนรู้ของเครื่อง เช่น sklearn, keras, chainer, ฯลฯ
ดังนั้นขอแค่รู้หลักการพื้นฐานแล้วที่เหลือก็ไปใช้มอดูลซึ่งถูกทำมาไว้ดีแล้ว
การวิเคราะห์การถดถอยโลจิสติกนี้โดยพื้นฐานแล้วเอาไว้แบ่งหมวดหมู่ข้อมูลออกเป็นสองหมวด แต่ก็สามารถนำไปประยุกต์ต่อยอดเป็นการแบ่งกี่หมวดก็ได้
และนอกจากนี้แล้วยังมีเทคนิคอื่นๆอีกมากมาย หากมีโอกาสจะเขียนถึงในคราวต่อไป
อ้างอิง
หลังจากที่ลองซื้อหนังสือมาอ่านๆหลายเล่มอีกทั้งเปิดอ่านตามเว็บต่างๆก็อยากลองเขียนสรุปความรู้ที่ตัวเองได้ลงบล็อกสักหน่อย
เพียงแต่เรื่องนี้เป็นศาสตร์ที่มีรายละเอียดมากมาย หากจะอธิบายตั้งแต่ต้นจริงๆคงต้องรอคนที่เป็นเฉพาะทางมาเขียนมากกว่า (ซึ่งค่อนข้างคาดหวังอยากให้มี เพราะเรื่องนี้ขาดแคลนคนเขียนเป็นภาษาไทยมาก) ในที่นี้คงจะอธิบายละเอียดแค่เท่าที่จะพอทำได้
นี่เป็นบทความแรกที่จะเขียนถึงเรื่องการเรียนรู้ของเครื่อง จากนี้ไปก็ตั้งใจว่าจะเขียนอีกหลายเรื่องต่อไป
เทคนิคการเรียนรู้ของเครื่องมีอยู่หลากหลายรูปแบบมาก แต่ในที่นี้จะเริ่มแนะนำเรื่องของการวิเคราะห์การถดถอยโลจิสติก (逻辑回归, logistic regression) ซึ่งเป็นวิธีการที่นิยมใช้เพื่อจำแนกประเภทข้อมูลหรือสิ่งของบางอย่างออกเป็นสองกลุ่ม
สำหรับเรื่องที่พื้นฐานกว่านั้นเช่นว่า "การวิเคราะห์ถดถอย" คืออะไร มีเขียนเอาไว้ในบทความเรื่อง "การวิเคราะห์การถดถอยเชิงเส้นด้วยการเคลื่อนลงตามความชัน" https://phyblas.hinaboshi.com/20161210 ซึ่งเขียนขึ้นมาทีหลัง แนะนำให้อ่านในนั้นก่อนแล้วค่อยมาอ่านหน้านี้อาจจะดีกว่า
ขอเริ่มจากยกปัญหาโดยลองสมมุติสถานการณ์ง่ายๆ
มีที่ดินอยู่แปลงหนึ่ง ขนาด 40x30 เมตร อยากทดสอบว่าดินบริเวณไหนอุดมสมบูรณ์ก็เลยลองหว่านเมล็ดถั่วไปพันเมล็ดโดยสุ่มตำแหน่ง ผลปรากฏมาตามนี้

สีเขียวคือต้นถั่วงอก สีเหลืองคือต้นถั่วไม่งอก จะเห็นว่าแบ่งเขตกันชัดเจน ดูด้วยตาก็คงพอกะได้คร่าวๆว่าจะแบ่งเขตยังไงดี
เฉลย... ความจริงแล้วพื้นที่นี้สามารถอธิบายได้ง่ายๆด้วยสมการนี้ นั่นคือเมื่อ x-2y+10>0 ถั่วจะงอก
และภาพนี้ก็ได้มาจากการเขียนโค้ดตามนี้
import numpy as np
import matplotlib.pyplot as plt
x_thua = np.random.uniform(0,40,1000) # สุ่มค่า x ตั้งแต่ 0 ถึง 40 มา 1000 ค่า
y_thua = np.random.uniform(0,30,1000) # สุ่มค่า y ตั้งแต่ 0 ถึง 30 มา 1000 ค่า
ngokmai = np.array(x_thua-2*y_thua+10>0,dtype=int) # กำหนดว่าจะงอกมั้ยโดยดูจากค่าตำแหน่งแกน x และ y
plt.axes(aspect=1,xlim=[0,40],ylim=[0,30],xlabel='x',ylabel='y')
plt.scatter(x_thua,y_thua,c=ngokmai,s=50,edgecolor='k',cmap='summer_r')
plt.show()
import matplotlib.pyplot as plt
x_thua = np.random.uniform(0,40,1000) # สุ่มค่า x ตั้งแต่ 0 ถึง 40 มา 1000 ค่า
y_thua = np.random.uniform(0,30,1000) # สุ่มค่า y ตั้งแต่ 0 ถึง 30 มา 1000 ค่า
ngokmai = np.array(x_thua-2*y_thua+10>0,dtype=int) # กำหนดว่าจะงอกมั้ยโดยดูจากค่าตำแหน่งแกน x และ y
plt.axes(aspect=1,xlim=[0,40],ylim=[0,30],xlabel='x',ylabel='y')
plt.scatter(x_thua,y_thua,c=ngokmai,s=50,edgecolor='k',cmap='summer_r')
plt.show()
จะเห็นว่าถ้ารู้สมการแล้วที่เหลือต่อไปนี้เราก็รู้แล้วว่าควรจะปลูกถั่วตรงไหน อย่างไรก็ตามปัญหาก็คือหากเราไม่รู้สมการมาก่อนเราจะทำอย่างไรจึงจะรู้มันได้โดยดูจากแค่ผลของการปลูกถั่วดังในภาพนี้
นั่นล่ะคือหน้าที่ของเทคนิคการวิเคราะห์การถดถอยโลจิสติก
สมมุติว่าถ้าเขตของพื้นที่ถูกแบ่งเป็นเส้นตรงชัดเจนอย่างในตัวอย่างนี้ เราอาจกำหนดฟังก์ชันตัดสินขึ้นมา
..(1)
โดยให้จุดที่ฟังก์ชันตัดสิน f(x,y)=0 เป็นเส้นแบ่งเขต และทำการวิเคราะห์เพื่อหาค่า a, b และ c
ในที่นี้ a กับ b จะถูกเรียกว่าสัมประสิทธิ์น้ำหนัก และ c เรียกว่าเป็นไบแอส
น้ำหนักในที่นี้คนละความหมายกับน้ำหนักตัวของคนหรือสิ่งของ แต่มีความหมายทำนองเดียวกับน้ำหนักเวลาคำนวนค่าทางสถิติ คือหมายถึงความสำคัญหรือสิ่งที่จะบอกว่าค่าข้างหลังมันจะส่งผลถึงค่าของฟังก์ชันมากน้อยแค่ไหน มีผลในทิศทางไหน
ส่วนไบแอสคือค่าศูนย์สำหรับยืนพื้น ในที่นี้เป็นตัวกำหนดว่ากราฟเส้นแบ่งจะเลื่อนไปทางซ้ายขวาบนล่างแค่ไหนโดยไม่เกี่ยวกับความชันเส้นแบ่ง ถ้าไบแอสเป็น 0 กราฟก็จะผ่านจุด 0,0
กรณีตัวอย่างนี้ ผลเฉลยค่า a, b และ c ที่ได้นั้นสุดท้ายควรจะมีความสัมพันธ์ในลักษณะที่เป็น b/a=-2 และ c/a=10
วิธีการที่ใช้กันทั่วไปในการหาค่าเหล่านี้ก็คือ กำหนดค่าเริ่มต้นอะไรก็ได้ไปก่อน แล้วดูว่าผลที่ได้ใกล้เคียงแค่ไหน จากนั้นก็ค่อยๆปรับตัวเลขให้ได้ค่าใกล้เคียงขึ้นไปเรื่อยๆ
การจะดูว่าผลที่ได้นั้นใกล้เคียงแค่ไหน วิธีการง่ายสุดก็คือนับจำนวนที่ทายถูก
เช่น ลองทดสอบโดยเอาข้อมูลผลการปลูกถั่วที่เก็บไว้ในตัวอย่างข้างต้นมาใช้ จากโค้ดที่แล้วข้อมูลถูกเก็บอยู่ใน x_thua, y_thua และ ngokmai เราอาจทำการบันทึกเก็บไว้ก่อนเพื่อนำมาใช้ทีหลัง การบันทึกอาเรย์ทีเดียวหลายตัวเราอาจใช้คำสั่ง np.savez ของ numpy
np.savez('plukthua.npz',x=x_thua,y=y_thua,z=ngokmai)
จากนั้นเราจะดึงไฟล์ .npz ที่บันทึกไว้มาใช้งานได้ด้วยคำสั่ง np.load (รายละเอียดมากกว่านี้อ่านได้ใน numpy เบื้องต้นบทที่ ๓๙)
เช่น ลองสมมุติให้ a=3, b=-15, c=129.3 แล้วลองวาดดูว่าผลเป็นอย่างไร
a = 3
b = -15
c = 129.3
# ดึงข้อมูลผลการปลูกถั่วที่บันทึกไว้มาใช้
plukthua = np.load('plukthua.npz')
x_thua = plukthua['x']
y_thua = plukthua['y']
ngokmai = plukthua['z']
# ทำการทายผลด้วยค่า a,b,c ที่เรากำหนดขึ้นดู
ngokmang = np.array(a*x_thua+b*y_thua+c>0,dtype=int)
# เทียบผลดูว่าถูกไหม
thukmai = np.array(ngokmang==ngokmai,dtype=int)
# วาดเส้นแบ่งเขตและลงสีส่วนล่าง
x_sen = np.array([0,40])
y_sen = -(c+a*x_sen)/b
plt.axes(aspect=1,xlim=[0,40],ylim=[0,30],xlabel='x',ylabel='y')
plt.fill_between(x_sen,y_sen,color='#00aa00')
# วาดจุดที่ทายถูก
plt.scatter(x_thua[thukmai==1],y_thua[thukmai==1],c=ngokmai[thukmai==1],s=50,edgecolor='k',cmap='summer_r')
# วาดจุดที่ทายผิด (ขอบแดง)
plt.scatter(x_thua[thukmai==0],y_thua[thukmai==0],c=ngokmai[thukmai==0],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()
print('ทายถูกทั้งหมด %d จาก 1000'%thukmai.sum())
b = -15
c = 129.3
# ดึงข้อมูลผลการปลูกถั่วที่บันทึกไว้มาใช้
plukthua = np.load('plukthua.npz')
x_thua = plukthua['x']
y_thua = plukthua['y']
ngokmai = plukthua['z']
# ทำการทายผลด้วยค่า a,b,c ที่เรากำหนดขึ้นดู
ngokmang = np.array(a*x_thua+b*y_thua+c>0,dtype=int)
# เทียบผลดูว่าถูกไหม
thukmai = np.array(ngokmang==ngokmai,dtype=int)
# วาดเส้นแบ่งเขตและลงสีส่วนล่าง
x_sen = np.array([0,40])
y_sen = -(c+a*x_sen)/b
plt.axes(aspect=1,xlim=[0,40],ylim=[0,30],xlabel='x',ylabel='y')
plt.fill_between(x_sen,y_sen,color='#00aa00')
# วาดจุดที่ทายถูก
plt.scatter(x_thua[thukmai==1],y_thua[thukmai==1],c=ngokmai[thukmai==1],s=50,edgecolor='k',cmap='summer_r')
# วาดจุดที่ทายผิด (ขอบแดง)
plt.scatter(x_thua[thukmai==0],y_thua[thukmai==0],c=ngokmai[thukmai==0],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()
print('ทายถูกทั้งหมด %d จาก 1000'%thukmai.sum())

จากรูปนี้บริเวณที่พื้นสีเขียวคือที่ทำนายว่าจะอุดมสมบูรณ์ (จุดเป็นสีเขียว) โดยจุดที่ขอบสีแดงคือที่ทายผิด จะเห็นว่าส่วนใหญ่ทายถูกแล้ว ดังที่จะเห็นได้ว่าค่าที่ print ออกมาได้คือทายถูก 880 จาก 1000
เป้าหมายคือการปรับค่าให้จำนวนที่ผิดมีน้อยลง อย่างไรก็ตาม โดยทั่วไปแล้วแทนที่จะใช้จำนวนที่ทายถูกเป็นเป้าหมายโดยตรง วิธีที่นิยมกว่ากลับเป็นการคำนวณค่าความคลาดเคลื่อนรวม แล้วพยายามปรับให้ความคลาดเคลื่อนรวมน้อยที่สุด
ค่าความคลาดเคลื่อนรวมมักถูกเรียกว่าเป็นค่าเสียหาย (cost หรือ loss) คือเป็นค่าที่จะยิ่งมากขึ้นเมื่อคำนวณหรือทำนายผิด
ค่าเสียหายที่นิยมใช้คือค่าความคลาดเคลื่อนกำลังสองเฉลี่ย (sum of squared error มักย่อว่า SSE) การนำค่าที่ทำนายได้ (ในที่นี้คือ ngokmai) กับค่าจริงๆ (ในที่นี้คือ ngokmang) มาลบกันแล้วยกกำลังสอง จากนั้นก็คิดค่าของทุกจุดแล้วเอามารวมกัน
สามารถคำนวนความคลาดเคลื่อนกำลังสองของแต่ละตัวได้โดย
print((ngokmang-ngokmai)**2)
จะได้ค่าที่เป็น 0 และ 1 สลับกันไป อันที่เป็น 0 คือที่ทายถูก ที่เป็น 1
ดังนั้นแล้วเราสามารถคำนวณ SSE ได้ด้วยการเอาทุกตัวมารวมกัน
sse = ((ngokmang-ngokmai)**2).sum()
อย่างไรก็ตามการที่ให้ทายถูกแล้วเป็น 0 ทายผิดแล้วเป็น 1 แบบนี้เป็นลักษณะของฟังก์ชันขั้นบันได เป็นการแบ่งที่หยาบไปสักหน่อย ในความเป็นจริงที่เรามักจะเจอกันมากกว่าก็คือให้คะแนนความคลาดเคลื่อนในระดับที่ละเอียดกว่านี้
ลองย้อนกลับไปดูตอนแรกที่เราหาค่า ngokmang นั้นเราใช้ a*x_thua+b*y_thua+c มาเทียบว่ามากกว่า 0 หรือเปล่า ถ้ามากกว่าให้เป็น 1 ถ้าน้อยกว่าเป็น 0
แต่คราวนี้แทนที่จะทำอย่างนั้นเราลองเปลี่ยนเป็นว่าถ้ามากกว่า 0 ไปมากๆจึงจะเข้าใกล้ 1 ถ้าน้อยกว่า 0 มากๆให้เข้าใกล้ 0 แต่ถ้าค่าใกล้ๆ 0 ก็ให้มีค่าที่ประมาณ 0.5
ฟังก์ชันที่มีลักษณะเป็นแบบนี้ที่นิยมใช้คือฟังก์ชันซิกมอยด์ (sigmoid)
..(2)
เพื่อให้เห็นภาพลองเอาฟังก์ชันมาเขียนกราฟ เปรียบเทียบกับกราฟแบบขั้นบันไดที่แบ่ง 0 กับ 1 แบบตัดกันชัดเจนแบบเดิมดูด้วย
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.linspace(-8,8,1001)
plt.axes(yticks=np.linspace(0,1,11))
plt.plot(x,x>0)
plt.plot(x,sigmoid(x))
plt.grid()
plt.show()
return 1/(1+np.exp(-x))
x = np.linspace(-8,8,1001)
plt.axes(yticks=np.linspace(0,1,11))
plt.plot(x,x>0)
plt.plot(x,sigmoid(x))
plt.grid()
plt.show()

เส้นสีเขียวคือซิกมอยด์ จะเห็นว่ามีการเปลี่ยนแปลงแบบค่อยๆเป็นค่อยๆไป แต่เมื่อมีค่ามากๆก็จะลู่เข้า 1 และเมื่อน้อยมากๆจะลู่เข้า 0
ที่มักใช้แบบนี้เพราะในปัญหาการจำแนกประเภทโดยทั่วไปถ้าฟังก์ชันคำนวณได้ใกล้ 0 แสดงว่าค่าที่คำนวณได้ก็อยู่ใกล้ขอบเขตแบ่งทำให้จริงๆแล้วมันมีโอกาสที่จะอยู่ฝั่งไหนก็ได้ บางทีแทนที่จะตัดสินตูมเดียวไปเลยว่าเป็น 0 หรือ 1 การตัดสินให้ค่าเป็นตัวเลขอยู่ในช่วงระหว่าง 0 ถึง 1 จะดูประนีประนอมกว่า
ในกรณีตัวอย่างนี้ f(x) = ax+bx+c เป็นฟังก์ชันตัดสินของเรา ซึ่งอาจให้ค่าอะไรก็ได้ตั้งแต่ลบอนันต์ถึงอนันต์ ยิ่งค่ามากยิ่งมีโอกาสเป็นดินดีมาก แต่ถ้าค่าใกล้ 0 ก็อาจก้ำกึ่ง
กรณีนี้ฟังก์ชันเป้าหมายที่ผ่านฟังก์ชันซิกมอยด์แล้วสามารถตีความได้ว่าเป็นความน่าจะเป็นที่บริเวณนั้นจะเป็นดินดี ซึ่งแสดงได้ว่าถ้า sigmoid(0)=0.5 หมายความว่าโอกาสเป็นคือ 50:50
ลองวาดแผนภาพไล่สีดูเปรียบเทียบระหว่างสองแบบ
x,y = np.meshgrid(np.linspace(0,40,160),np.linspace(0,30,120))
plt.figure(figsize=[8,3])
plt.axes([0.05,0.03,0.4,0.95],aspect=1,title='$sigmoid(x-2y+10)$',xlim=[0,40],ylim=[0,30])
plt.pcolormesh(x,y,sigmoid(x-2*y+10),cmap='coolwarm_r')
plt.axes([0.5,0.03,0.4,0.95],aspect=1,title='$x-2y+10>0$',xlim=[0,40],ylim=[0,30])
plt.pcolormesh(x,y,x-2*y+10>0,cmap='coolwarm_r')
plt.colorbar(cax=plt.axes([0.92,0.03,0.03,0.93]))
plt.show()
plt.figure(figsize=[8,3])
plt.axes([0.05,0.03,0.4,0.95],aspect=1,title='$sigmoid(x-2y+10)$',xlim=[0,40],ylim=[0,30])
plt.pcolormesh(x,y,sigmoid(x-2*y+10),cmap='coolwarm_r')
plt.axes([0.5,0.03,0.4,0.95],aspect=1,title='$x-2y+10>0$',xlim=[0,40],ylim=[0,30])
plt.pcolormesh(x,y,x-2*y+10>0,cmap='coolwarm_r')
plt.colorbar(cax=plt.axes([0.92,0.03,0.03,0.93]))
plt.show()

จะสังเกตได้ว่าต่างกันแค่ที่บริเวณใกล้รอยต่อ ซิกมอยด์จะค่อยๆไล่สี ไม่ได้ตัดเปลี่ยนไปทันทีแบบฟังก์ชันขั้นบันได
ซึ่งหมายความว่าถ้าห่างจากรอยต่อมากๆเราจะตัดสินได้ทันทีว่าอยู่กลุ่มไหน แต่ถ้าอยู่แถวๆรอยต่อค่าก็จะก้ำกึ่ง มีความเป็นไปได้ที่จะอยู่กลุ่มไหนก็ได้
ฟังก์ชันซิกมอยด์ในที่นี้เรียกว่าทำหน้าที่เป็นฟังก์ชันกระตุ้น (activation function)
ฟังก์ชันกระตุ้นที่นิยมใช้ยังมีอีกหลากหลายแบบ เช่น relu, tanh, ฯลฯ ซึ่งก็เหมาะใช้ในกรณีต่างกันออกไป
ฟังก์ชันกระตุ้นแบบนี้จะใช้เมื่อตอนคำนวณความควรจะเป็นของค่าที่ทำนายได้เท่านั้น แต่ในผลลัพธ์สุดท้ายแล้วค่าจริงมีเพียง 0 กับ 1 ดังนั้นเมื่อจะเทียบกับค่าจริงว่าทายถูกหรือผิดยังไงก็ต้องมาดูว่าค่ามากหรือน้อยกว่า 0.5 เพื่อแบ่งเป็น 0 หรือ 1
สรุปแล้วสิ่งที่ต้องเปลี่ยนตอนนี้คือ เปลี่ยนค่าทำนายจากเดิมมาเป็น
ngokmang = sigmoid(a*x_thua+b*y_thua+c)
พอลองดูค่า ngokmang ที่ได้แล้วก็จะพบว่าค่าส่วนใหญ่จะกองกันอยู่ที่ใกล้ 0 และใกล้ 1 แต่ก็จะไม่เป็น 0 หรือ 1 พอดีซะทีเดียว
จากนั้นก็คำนวณค่าเสียหายใหม่อีกที
sse = ((ngokmai-ngokmang)**2).sum()
ค่าเสียหายนี้ตามหนังสือมักแทนด้วยตัว J หากนำค่าเสียหาย SSE เขียนในรูปสมการคณิตศาสตร์จะได้เป็น
..(3)
โดย n คือจำนวนจุดข้อมูลทั้งหมด z(i) คือค่าคำตอบจริงของแต่ละจุด (เป็น 0 หรือ 1) ส่วน φ(i) คือค่าที่คำนวณได้ในแต่ละจุด ในที่นี้มาจากฟังก์ชันซิกมอยด์
..(4)
ในที่นี้เป็นการเขียนในรูปทั่วไป ไม่ได้จำกัดอยู่แค่ ๒ มิติ แต่ให้มี m มิติ ฟังก์ชันตัดสิน f(x(i)) = f(x1,(i),x2,(i),...,xm,(i)) จะเขียนใหม่เป็น
..(5)
wj คือค่าน้ำหนักของตัวแปรต้นแต่ละตัว โดยหากเทียบกับสมการ (1) แล้วในที่นี้เรามีตัวแปรต้น ๓ ตัว แบ่งเป็นน้ำหนักในแกน x ในที่นี้คือ w1=wx=a และน้ำหนักแกน y คือ w2=wy=b ส่วนไบแอส c ในที่นี้เขียนแทนด้วย w0 โดยต่อจากนี้จะเขียน a เป็น wx เขียน b เป็น wy และ c เป็น w0 เพื่อความเข้าใจง่าย
ตอนนี้เราเข้าใจแล้วว่าเป้าหมายคือการเปลี่ยนแปลงค่าน้ำหนักและค่าไบแอสให้ค่า SSE นี้น้อยที่สุด เพื่อการนั้นขั้นต่อไปคือต้องใช้วิธีการที่เรียกว่าการเคลื่อนลงตามความชัน (gradient descent, GD)
***หมายเหตุ ส่วนตรงนี้ต้องใช้ความรู้แคลคูลัสระดับมหาวิทยาลัย ใครไม่สนใจคณิตศาสตร์อาจข้ามไปอ่านส่วนของโค้ดได้เลย
หลักการของวิธีนี้คือหาค่าความชันของฟังก์ชันเทียบกับตัวแปรแต่ละตัว หรือก็คืออนุพันธ์ย่อย จากนั้นปรับเปลี่ยนค่าไปในทางที่ตรงกันข้ามกับความชัน
นั่นคือความเปลี่ยนแปลงของน้ำหนักคำนวณโดย
..(6)
หรือเขียนเป็นภาษาพูดได้ว่า
การเปลี่ยนแปลงค่าน้ำหนัก = -อัตราการเรียนรู้ x ความชันของค่าเสียหายเทียบกับค่าน้ำหนักตัวนั้น
อัตราการเรียนรู้ (η) คือค่าที่จะกำหนดว่าในแต่ละรอบที่คำนวณจะมีการปรับเปลี่ยนค่าน้ำหนักไปมากแค่ไหน
ค่านี้เป็นค่าที่ผู้เขียนโปรแกรมจะต้องกำหนดขึ้นเองให้พอเหมาะ ถ้าหากมากไปค่าจะถูกปรับเยอะไปจนอาจเลยค่าที่เหมาะสมและปรับเท่าไหร่ก็ไม่อาจได้ค่าที่ต้องการได้เลย แต่ถ้าน้อยไปก็จะใช้เวลานานมากกว่าจะลู่เข้าสู่คำตอบที่ต้องการ
ค่าความคลาดเคลื่อนในที่นี้ใช้เป็น SSE แต่ในกรณีอื่นก็อาจใช้อย่างอื่นได้อีก ที่จริงแล้วกรณีปัญหาการถดถอยโลจิสติกมักนิยมใช้ค่าที่เรียกว่าเอนโทรปีไขว้ (cross entropy) มากกว่า แต่ในที่นี้ขอใช้ SSE เนื่องจากเข้าใจง่ายกว่า
ความชันของค่าเสียหาย J ในกรณีที่ J เป็น SSE ดังสมการ (3) เมื่อทำการหาอนุพันธ์ย่อยสำหรับ wj และ w0 ออกมาจะได้เป็น
..(7)
และ
..(8)
ซึ่งสมการ (7) สำหรับ wx และ wy ในตัวอย่างนี้จะได้
..(9)
เมื่อแทนค่าสมการ (8) และ (9) ลงในสมการ (6) ก็จะหาค่าความชันที่ควรเปลี่ยนแปลงไปได้เป็น
..(10)
หากใครไม่สามารถเข้าใจกับคณิตศาสตร์ที่อธิบายมาตรงนี้ก็ขอสรุปสั้นๆแค่ว่าสิ่งที่เราต้องการคือสมการ (10) เพื่อไว้ใช้หาค่าการเปลี่ยนแปลงของความชันและไบแอสในแต่ละรอบ
เมื่ออธิบายทฤษฎีคร่าวๆจนพอรู้แนวทางแล้ว ทีนี้มาลองเขียนโค้ดกันดูเลย
def sigmoid(x):
return 1/(1+np.exp(-x))
eta = 0.0001 # อัตราการเรียนรู้
n_thamsam = 10000 # จำนวนครั้งที่ทำซ้ำเพื่อปรับค่าน้ำหนักและไบแอส
plukthua = np.load('plukthua.npz')
x_thua = plukthua['x']
y_thua = plukthua['y']
ngokmai = plukthua['z']
# ค่าน้ำหนักเริ่มต้น
wx,wy,w0 = 0,0,0
# คำนวณค่าที่ได้จากการทำนายตอนแรกสุด
ngokmang = sigmoid(wx*x_thua+wy*y_thua+w0)
sse = [] # เตรียมลิสต์เก็บค่า sse
thuktong = [] # เตรียมลิสต์เก็บค่าจำนวนครั้งที่ทายถูก
# เริ่มการทำซ้ำเพื่อปรับค่าน้ำหนัก
for i in range(n_thamsam):
# ปรับค่าน้ำหนัก
eee = 2*ngokmang*(1-ngokmang)*(ngokmai-ngokmang)
wx += (eee*x_thua).sum()*eta
wy += (eee*y_thua).sum()*eta
w0 += eee.sum()*eta
# คำนวณฟังก์ชันกระตุ้น
ngokmang = sigmoid(wx*x_thua + wy*y_thua + w0)
# คำนวณ sse แล้วเก็บใส่ลิสต์
sse += [((ngokmang-ngokmai)**2).sum()]
# เทียบว่าอันไหนทายถูกบ้าง
thukmai = np.array(np.abs(ngokmai-ngokmang)<0.5,dtype=int)
# นับจำนวนว่าถูกกี่อันแล้วเก็บใส่ลิสต์
thuktong += [thukmai.sum()]
x_sen = np.array([0,40])
y_sen = -(w0+wx*x_sen)/wy
plt.axes(aspect=1,xlim=[0,40],ylim=[0,30],xlabel='x',ylabel='y')
plt.fill_between(x_sen,y_sen,color='#00aa00')
plt.scatter(x_thua[thukmai==1],y_thua[thukmai==1],c=ngokmai[thukmai==1],s=50,edgecolor='k',cmap='summer_r')
plt.scatter(x_thua[thukmai==0],y_thua[thukmai==0],c=ngokmai[thukmai==0],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()
print('ได้สมการเส้นแบ่งเขตเป็น %.3fx%+.3fy%+.3f = 0'%(wx,wy,w0))
print('ทายถูกทั้งหมด %d จาก %d'%(thukmai.sum(),len(x_thua)))
return 1/(1+np.exp(-x))
eta = 0.0001 # อัตราการเรียนรู้
n_thamsam = 10000 # จำนวนครั้งที่ทำซ้ำเพื่อปรับค่าน้ำหนักและไบแอส
plukthua = np.load('plukthua.npz')
x_thua = plukthua['x']
y_thua = plukthua['y']
ngokmai = plukthua['z']
# ค่าน้ำหนักเริ่มต้น
wx,wy,w0 = 0,0,0
# คำนวณค่าที่ได้จากการทำนายตอนแรกสุด
ngokmang = sigmoid(wx*x_thua+wy*y_thua+w0)
sse = [] # เตรียมลิสต์เก็บค่า sse
thuktong = [] # เตรียมลิสต์เก็บค่าจำนวนครั้งที่ทายถูก
# เริ่มการทำซ้ำเพื่อปรับค่าน้ำหนัก
for i in range(n_thamsam):
# ปรับค่าน้ำหนัก
eee = 2*ngokmang*(1-ngokmang)*(ngokmai-ngokmang)
wx += (eee*x_thua).sum()*eta
wy += (eee*y_thua).sum()*eta
w0 += eee.sum()*eta
# คำนวณฟังก์ชันกระตุ้น
ngokmang = sigmoid(wx*x_thua + wy*y_thua + w0)
# คำนวณ sse แล้วเก็บใส่ลิสต์
sse += [((ngokmang-ngokmai)**2).sum()]
# เทียบว่าอันไหนทายถูกบ้าง
thukmai = np.array(np.abs(ngokmai-ngokmang)<0.5,dtype=int)
# นับจำนวนว่าถูกกี่อันแล้วเก็บใส่ลิสต์
thuktong += [thukmai.sum()]
x_sen = np.array([0,40])
y_sen = -(w0+wx*x_sen)/wy
plt.axes(aspect=1,xlim=[0,40],ylim=[0,30],xlabel='x',ylabel='y')
plt.fill_between(x_sen,y_sen,color='#00aa00')
plt.scatter(x_thua[thukmai==1],y_thua[thukmai==1],c=ngokmai[thukmai==1],s=50,edgecolor='k',cmap='summer_r')
plt.scatter(x_thua[thukmai==0],y_thua[thukmai==0],c=ngokmai[thukmai==0],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()
print('ได้สมการเส้นแบ่งเขตเป็น %.3fx%+.3fy%+.3f = 0'%(wx,wy,w0))
print('ทายถูกทั้งหมด %d จาก %d'%(thukmai.sum(),len(x_thua)))
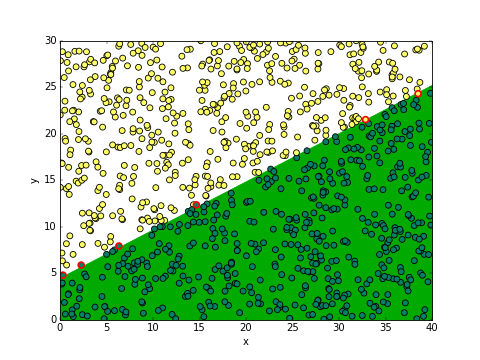
เมื่อรันแล้วก็จะได้ผลออกมาเป็นภาพนี้

ผลที่ได้อาจต่างไปโดยขึ้นกับตำแหน่ง x และ y ของต้นถั่วที่สุ่มมาตอนแรกสุด แต่โดยรวมแล้วแนวโน้มควรจะเหมือนกันคือทายถูกเกือบหมด
สำหรับกรณีของข้อมูลสุ่มชุดนี้ผลที่ได้จะเห็นว่าถูก 994 แสดงว่าผิดแค่ 6 เท่านั้น ดังที่จะเห็นได้ว่ามีจุดขอบแดงอยู่ 6 จุด
สมการที่ได้ก็คือ 0.582x-1.123y+5.066 = 0 ซึ่งก็สอดคล้องกับที่ควรจะเป็นนั่นคือ wy/wx ประมาณ -2 และ w0/wx ประมาณ 10
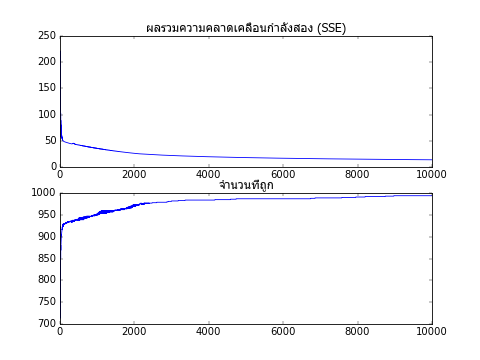
ค่าความคลาดเคลื่อนรวมและจำนวนที่ทายถูกในแต่ละขั้นได้ถูกเก็บไว้ในตัวแปร sse และ thuktong ลองเอามาวาดกราฟแสดงการเปลี่ยนแปลงของค่า
ax = plt.subplot(211)
ax.set_title(u'ผลรวมความคลาดเคลื่อนกำลังสอง (SSE)',fontname='Tahoma')
plt.plot(sse)
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(thuktong)
plt.show()
ax.set_title(u'ผลรวมความคลาดเคลื่อนกำลังสอง (SSE)',fontname='Tahoma')
plt.plot(sse)
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(thuktong)
plt.show()

จะเห็นว่ายิ่งผ่านไปหลายๆรอบความคลาดเคลื่อนรวมยิ่งลดลง และจำนวนครั้งที่ทายถูกก็มากขึ้น
ตอนนี้สามารถเขียนโค้ดสำหรับการเรียนรู้ของเครื่องสำหรับการวิเคราะห์การถดถอยโลจิสติกได้แล้ว แต่อย่างไรก็ตาม เพื่อให้เป็นระบบระเบียบมากขึ้น โดยทั่วไปแล้วการเขียนโดยใช้วิธีการสร้างคลาสจะสะดวกกว่าและเป็นที่นิยมมาก
ลองเขียนใหม่โดยใช้คลาสดูก็จะได้ประมาณนี้
class ThotthoiLogistic2d:
def __init__(self,eta):
self.eta = eta # อัตราการเรียนรู้
# เรียนรู้
def rianru(self,x,y,z,n_thamsam):
self.sse = []
self.thuktong = []
# ค่าน้ำหนักเริ่มต้น
self.wx,self.wy,self.w0 = 0,0,0
phi = self.ha_sigmoid(x,y)
for i in range(n_thamsam):
# ปรับค่าน้ำหนัก
eee = 2*phi*(1-phi)*(z-phi)
self.wx += (eee*x_thua).sum()*self.eta
self.wy += (eee*y_thua).sum()*self.eta
self.w0 += eee.sum()*self.eta
phi = self.ha_sigmoid(x,y)
# บันทึกผลในแต่ละรอบ
thukmai = np.abs(phi-z)<0.5
self.thuktong += [thukmai.sum()]
self.sse += [self.ha_sse(x,y,z)]
# ทำนายผล
def thamnai(self,x,y):
return self.ha_sigmoid(x,y)>0.5
# ฟังก์ชันกระตุ้น
def ha_sigmoid(self,x,y):
return sigmoid(self.wx*x + self.wy*y + self.w0)
# หาค่าเสียหาย
def ha_sse(self,x,y,z):
return ((z-self.ha_sigmoid(x,y))**2).sum()
def __init__(self,eta):
self.eta = eta # อัตราการเรียนรู้
# เรียนรู้
def rianru(self,x,y,z,n_thamsam):
self.sse = []
self.thuktong = []
# ค่าน้ำหนักเริ่มต้น
self.wx,self.wy,self.w0 = 0,0,0
phi = self.ha_sigmoid(x,y)
for i in range(n_thamsam):
# ปรับค่าน้ำหนัก
eee = 2*phi*(1-phi)*(z-phi)
self.wx += (eee*x_thua).sum()*self.eta
self.wy += (eee*y_thua).sum()*self.eta
self.w0 += eee.sum()*self.eta
phi = self.ha_sigmoid(x,y)
# บันทึกผลในแต่ละรอบ
thukmai = np.abs(phi-z)<0.5
self.thuktong += [thukmai.sum()]
self.sse += [self.ha_sse(x,y,z)]
# ทำนายผล
def thamnai(self,x,y):
return self.ha_sigmoid(x,y)>0.5
# ฟังก์ชันกระตุ้น
def ha_sigmoid(self,x,y):
return sigmoid(self.wx*x + self.wy*y + self.w0)
# หาค่าเสียหาย
def ha_sse(self,x,y,z):
return ((z-self.ha_sigmoid(x,y))**2).sum()
จากนั้นเริ่มการใช้งานโดยสร้างออบเจ็กต์จากคลาส จากนั้นใช้เมธอด rianru เพื่อให้ออบเจ็กต์ทำการเรียนรู้และปรับค่าน้ำหนัก
eta = 0.0001 # อัตราการเรียนรู้
n_thamsam = 10000 # จำนวนครั้งที่ทำซ้ำ
# ดึงข้อมูลที่เก็บไว้มาใช้
plukthua = np.load('plukthua.npz')
x_thua = plukthua['x']
y_thua = plukthua['y']
ngokmai = plukthua['z']
# สร้างออบเจ็กต์
tl = ThotthoiLogistic2d(eta)
# เริ่มการเรียนรู้
tl.rianru(x_thua,y_thua,ngokmai,n_thamsam)
n_thamsam = 10000 # จำนวนครั้งที่ทำซ้ำ
# ดึงข้อมูลที่เก็บไว้มาใช้
plukthua = np.load('plukthua.npz')
x_thua = plukthua['x']
y_thua = plukthua['y']
ngokmai = plukthua['z']
# สร้างออบเจ็กต์
tl = ThotthoiLogistic2d(eta)
# เริ่มการเรียนรู้
tl.rianru(x_thua,y_thua,ngokmai,n_thamsam)
เสร็จแล้วก็นำมาวาดกราฟผลการเรียนรู้ดู โดยค่าจะเก็บอยู่ในแอตทริบิวต์ sse และ thuktong ของออบเจ็กต์ นำมาใช้ได้เลย
ax = plt.subplot(211)
ax.set_title(u'ผลรวมความคลาดเคลื่อนกำลังสอง (SSE)',fontname='Tahoma')
plt.plot(tl.sse)
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
plt.show()
print('ทายถูกทั้งหมด %d จาก %d'%(tl.thuktong[-1],len(ngokmai)))
ax.set_title(u'ผลรวมความคลาดเคลื่อนกำลังสอง (SSE)',fontname='Tahoma')
plt.plot(tl.sse)
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
plt.show()
print('ทายถูกทั้งหมด %d จาก %d'%(tl.thuktong[-1],len(ngokmai)))
ผลที่ได้จะเหมือนกันกับตอนที่ไม่ใช้คลาส
ค่าน้ำหนักก็อยู่ในแอตทริบิวต์ wx,wy,w0 นำมาแสดงผลได้ในลักษณะเดียวกัน
print('ได้สมการเส้นแบ่งเขตเป็น %.3fx%+.3fy%+.3f = 0'%(tl.wx,tl.wy,tl.w0))
ในที่นี้ที่ตั้งชื่อคลาสโดยมีคำว่า 2d ต่อท้ายก็เพราะว่าคลาสนี้ใช้กับกรณีที่ตัวแปรต้นมีแค่ ๒ ตัวเท่านั้น อย่างไรก็ตามปัญหาการแบ่งหมวดหมู่โดยทั่วไปอาจมีตัวแปรต้นกี่ตัวก็ได้ ดังนั้นเราลองมาปรับแก้อักสักหน่อยให้ใช้กับกี่ตัวแปรก็ได้
กรณีแบบนี้จะเป็นการสะดวกที่จะใช้ฟังก์ชัน np.dot ซึ่งใช้ในการคูณเมทริกซ์ ซึ่งถ้าใครไม่คุ้นเคยแล้วอาจจะเข้าใจยากขึ้นสักหน่อย แต่หากลองเทียบเคียงกับโค้ดในตัวอย่างบนก็จะเข้าใจง่ายขึ้น
ลองปรับแล้วก็จะออกมาแบบนี้
class ThotthoiLogistic:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam):
self.sse = []
self.thuktong = []
self.w = np.zeros(X.shape[1]+1)
phi = self.ha_sigmoid(X)
for i in range(n_thamsam):
eee = 2*phi*(1-phi)*(z-phi)
self.w[1:] += np.dot(X.T,eee)*self.eta
self.w[0] += eee.sum()*self.eta
phi = self.ha_sigmoid(X)
thukmai = np.abs(phi-z)<0.5
self.thuktong += [thukmai.sum()]
self.sse += [self.ha_sse(X,z)]
def thamnai(self,X):
return self.ha_sigmoid(X)>0.5
def ha_sigmoid(self,X):
return sigmoid(np.dot(X,self.w[1:])+self.w[0])
def ha_sse(self,X,z):
return ((z-self.ha_sigmoid(X))**2).sum()
# เริ่มการใช้งาน
eta = 0.0001
n_thamsam = 10000
plukthua = np.load('plukthua.npz')
x_thua = plukthua['x']
y_thua = plukthua['y']
ngokmai = plukthua['z']
# สร้างออบเจ็กต์
tl = ThotthoiLogistic(eta)
# ทำการรวมอาเรย์ของ x และ y ได้เป็นอาเรย์สองมิติ
xy_thua = np.stack([x_thua,y_thua],axis=1)
# เริ่มการเรียนรู้
tl.rianru(xy_thua,ngokmai,n_thamsam)
print('ได้สมการเส้นแบ่งเขตเป็น %.3fx%+.3fy%+.3f = 0'%(tl.w[1],tl.w[2],tl.w[0]))
print('ทายถูกทั้งหมด %d จาก %d'%(tl.thuktong[-1],len(ngokmai)))
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam):
self.sse = []
self.thuktong = []
self.w = np.zeros(X.shape[1]+1)
phi = self.ha_sigmoid(X)
for i in range(n_thamsam):
eee = 2*phi*(1-phi)*(z-phi)
self.w[1:] += np.dot(X.T,eee)*self.eta
self.w[0] += eee.sum()*self.eta
phi = self.ha_sigmoid(X)
thukmai = np.abs(phi-z)<0.5
self.thuktong += [thukmai.sum()]
self.sse += [self.ha_sse(X,z)]
def thamnai(self,X):
return self.ha_sigmoid(X)>0.5
def ha_sigmoid(self,X):
return sigmoid(np.dot(X,self.w[1:])+self.w[0])
def ha_sse(self,X,z):
return ((z-self.ha_sigmoid(X))**2).sum()
# เริ่มการใช้งาน
eta = 0.0001
n_thamsam = 10000
plukthua = np.load('plukthua.npz')
x_thua = plukthua['x']
y_thua = plukthua['y']
ngokmai = plukthua['z']
# สร้างออบเจ็กต์
tl = ThotthoiLogistic(eta)
# ทำการรวมอาเรย์ของ x และ y ได้เป็นอาเรย์สองมิติ
xy_thua = np.stack([x_thua,y_thua],axis=1)
# เริ่มการเรียนรู้
tl.rianru(xy_thua,ngokmai,n_thamsam)
print('ได้สมการเส้นแบ่งเขตเป็น %.3fx%+.3fy%+.3f = 0'%(tl.w[1],tl.w[2],tl.w[0]))
print('ทายถูกทั้งหมด %d จาก %d'%(tl.thuktong[-1],len(ngokmai)))
ในที่นี้ตัวแปร X จะแทนทั้ง x และ y ในโค้ดอันก่อน โดย X ในที่นี้เป็นอาเรย์สองมิติ สามารถสร้างขึ้นจาก x และ y ได้ด้วยฟังก์ชัน np.stack ดังที่เห็น ในตัวอย่างนี้รวมอยู่ในตัวแปรชื่อ xy_thua
พอทำแบบนี้แล้วตัวแปรสำหรับเมธอด rianru ก็จะลดลง แต่ใน X นี้จะแทนตัวแปรต้นกี่ตัวก็ได้ ไม่ใช่ว่าจะมีได้แค่สอง
ส่วน self.w ในที่นี้จะเก็บค่าน้ำหนักทั้งหมด (เทียบเท่า wx และ wy จากโค้ดที่แล้ว) รวมทั้งค่าไบแอส (เทียบเท่ากับ w0 จากโค้ดที่แล้ว) ด้วย พอเขียนรวมกันเป็นตัวแปรเดียวแบบนี้แล้วดูกะทัดรัดขึ้น
ขอส่งท้ายด้วยการทดสอบเกี่ยวกับอัตราการเรียนรู้ (eta) ซึ่งเป็นค่าที่สำคัญที่ต้องกำหนดให้พอเหมาะ
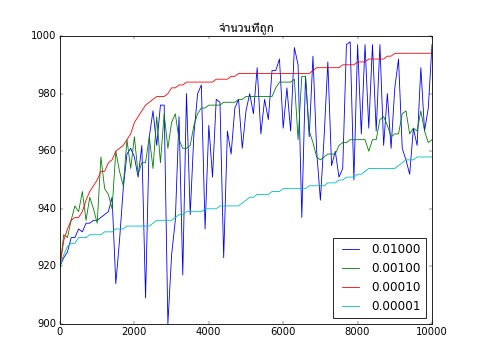
ลองนำคลาสที่เพิ่งสร้างมาใช้โดยปรับค่า eta ให้ต่างๆกันไป แล้ววาดกราฟเพื่อเปรียบเทียบการเรียนรู้ด้วยค่า eta ต่างๆดู
plt.title(u'จำนวนที่ถูก',fontname='Tahoma')
for eta in [0.01,0.001,0.0001,0.00001]:
tl = ThotthoiLogistic(eta)
tl.rianru(xy_thua,ngokmai,10001)
plt.plot(np.arange(0,10001,100),tl.thuktong[::100],label='%.5f'%eta)
plt.legend(loc=0)
plt.show()
for eta in [0.01,0.001,0.0001,0.00001]:
tl = ThotthoiLogistic(eta)
tl.rianru(xy_thua,ngokmai,10001)
plt.plot(np.arange(0,10001,100),tl.thuktong[::100],label='%.5f'%eta)
plt.legend(loc=0)
plt.show()

จากผลที่ได้จะเห็นว่าค่า 0.01 กับ 0.001 มากเกินไปจนทำให้ผลที่ได้แกว่งไปมาไม่อาจลู่เข้าสู่ค่าสูงสุดได้
ส่วน 0.00001 ก็น้อยไปทำให้การเปลี่ยนแปลงเป็นไปแบบช้ามาก กว่าจะลู่เข้าได้ก็ต้องทำซ้ำไปอีกนาน
ดังนั้นค่าที่เหมาะที่สุดคือ 0.0001
หากจะเขียนให้ซับซ้อนเพิ่มเติมขึ้นไปอีกแล้วอาจลองทำให้อัตราการเรียนรู้เปลี่ยนแปลงไปตามความเหมาะสม โดยลดลงเรื่อยๆเมื่อทำซ้ำ แบบนี้จะทำให้ช่วงแรกลู่เข้าได้เร็วแล้วช่วงหลังเข้าใกล้ค่าที่ต้องการได้มากที่สุด
สิ่งที่ควรปรับปรุงอีกก็เช่นเปลี่ยนฟังก์ชันค่าเสียหายจาก SSE มาเป็นอย่างอื่นเช่นเอนโทรปีไขว้
ในตัวอย่างทั้งหมดที่เขียนในนี้เป็นแค่พื้นฐานเบื้องต้น ยังมีอะไรๆต้องปรับปรุงอีกมากมายจึงจะเหมาะแก่การใช้งานจริงๆ
ในทางปฏิบัติแล้วปัจจุบันมีมอดูลหลายตัวในไพธอนที่มีฟังก์ชันและคลาสที่สำเร็จรูปเหมาะสำหรับการเรียนรู้ของเครื่อง เช่น sklearn, keras, chainer, ฯลฯ
ดังนั้นขอแค่รู้หลักการพื้นฐานแล้วที่เหลือก็ไปใช้มอดูลซึ่งถูกทำมาไว้ดีแล้ว
การวิเคราะห์การถดถอยโลจิสติกนี้โดยพื้นฐานแล้วเอาไว้แบ่งหมวดหมู่ข้อมูลออกเป็นสองหมวด แต่ก็สามารถนำไปประยุกต์ต่อยอดเป็นการแบ่งกี่หมวดก็ได้
และนอกจากนี้แล้วยังมีเทคนิคอื่นๆอีกมากมาย หากมีโอกาสจะเขียนถึงในคราวต่อไป
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib