[python] วิเคราะห์การถดถอยเชิงเส้นด้วยเทคนิคการเคลื่อนลงตามความชัน
เขียนเมื่อ 2016/12/10 18:04
แก้ไขล่าสุด 2022/07/21 15:29
ช่วงนี้เนื่องจากกำลังสนใจศึกษาเรื่องของศาสตร์ในการเรียนรู้ของเครื่องและการสร้างระบบโครงข่ายประสาทเทียมเพื่อวิเคราะห์ข้อมูลโดยอ่านตำราญี่ปุ่นหลายเล่ม ก็เลยเริ่มลองเขียนบล็อกสรุปสิ่งที่ตัวเองได้เรียนรู้ไป
ศาสตร์นี้มีเรื่องที่น่าเขียนถึงอยู่หลายอย่าง แต่ที่น่าพูดถึงมากที่สุดที่อยากเขียนถึงก็คือการวิเคราะห์การถดถอยโลจิสติก (逻辑回归, logistic regression) และการวิเคราะห์การถดถอยเชิงเส้น (线性回归, linear regression) ซึ่งใช้งานอย่างกว้างขวางและสามารถต่อยอดไปสู่เทคนิคอื่นๆที่ซับซ้อนขึ้นเช่นการสร้างระบบโครงข่ายประสาทได้
ก่อนหน้านี้ได้มีเขียนบทความแรกคือเรื่องการวิเคราะห์ถดถอยโลจิสติกไปแล้วใน https://phyblas.hinaboshi.com/20161103
แต่ในนั้นได้ข้ามรายละเอียดอะไรที่ควรเขียนถึงไปหลายอย่าง ที่สำคัญที่สุดอย่างหนึ่งก็คือ แต่ไหนแต่ไรแล้ว "การวิเคราะห์การถดถอย" หมายถึงอะไร
ดังนั้นในบทความนี้จะพูดถึงความหมายของการวิเคราะห์ถดถอย พร้อมทั้งทดลองเขียนโค้ดการวิเคราะห์ถดถอยอย่างง่ายสุด นั่นคือการวิเคราะห์ถดถอยแบบเชิงเส้น
การถดถอยเชิงเส้นนั้นนอกจากจะเป็นการถดถอยแบบง่ายที่สุดแล้ว ยังถูกนำไปต่อยอดเพื่อทำอะไรต่างๆได้มาก เช่นการวิเคราะห์การถดถอยโลจิสติกเพื่อการแบ่งกลุ่มข้อมูลนั้นที่จริงแล้วก็มีพื้นฐานอยู่บนการถดถอยเชิงเส้น
สำหรับใครที่อ่านบทความเรื่องการวิเคราะห์การถดถอยโลจิสติกอันนั้นไปก่อนแล้วจะลืมไปก่อนก็ได้ บทความในหน้านี้ไม่ได้ยืนพื้นจากบทความนั้น ในทางตรงกันข้าม แนะนำให้อ่านหน้านี้ก่อนแล้วค่อยไปอ่านตรงนั้นจะดีกว่า
การวิเคราะห์การถดถอยคืออะไร? อธิบายด้วยคำพูดทันทีอาจเข้าใจยาก ดังนั้นขอเริ่มด้วยการยกตัวอย่างสถานการณ์ที่สามารถใช้เพื่อแก้ปัญหาได้
โจทย์คือ สมมุติว่าซื้อลูกไดโนเสาร์มาตัวหนึ่ง เริ่มเลี้ยงมันตั้งแต่วันแรกที่ซื้อมา ในแต่ละวันไดโนเสาร์จะกินอาหารไปแค่ปริมาณหนึ่งแล้วก็อิ่ม
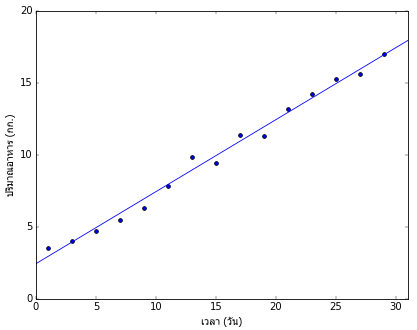
พอลองจดบันทึกปริมาณอาหารที่มันกินในแต่ละวันโดยบันทึกวันเว้นวันเป็นเวลาเดือนหนึ่งก็ได้ผลออกมาตามนี้
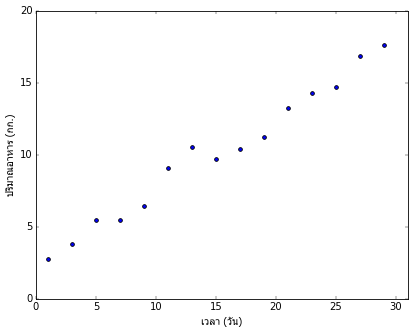
โดยแกนนอนคือเวลาในหน่วยวัน ส่วนแกนตั้งคือน้ำหนักของอาหารที่ต้องให้ในหน่วยกิโลกรัม
คำถามคือพอเห็นแนวโน้มแบบนี้แล้วเราสามารถทำนายได้หรือไม่ว่าวันถัดไปไดโนเสาร์จะกินอาหารกี่ กก.?
อีกทั้งในนี้เรามีการจดบันทึกแค่วันเว้นวัน เราจะบอกได้หรือไม่ว่าวันที่เราไม่ได้จดบันทึกนั้นมันกินอาหารไปกี่ กก.?
การหาคำตอบของปัญหาเหล่านี้ นั่นก็คือสิ่งที่เรียกว่าการวิเคราะห์การถดถอย
การวิเคราะห์การถดถอยก็คือ การวิเคราะห์หาความสัมพันธ์ระหว่างตัวแปรต้นกับตัวแปรตาม โดยวิเคราะห์จากข้อมูลที่มีอยู่โดยดูแนวโน้มต่างๆ แล้วทำนายว่าถ้าตัวแปรต้นมีค่าเท่านี้ ตัวแปรตามจะมีค่าเท่าใด
เช่นโจทย์ข้อนี้ ตัวแปรต้นคือเวลา (เดือน) ตัวแปรตามคือน้ำหนักอาหาร (กก.) เราต้องการทำนายว่าในวันไหนไดโนเสาร์จะกินอาหารเท่าไหร่
สำหรับข้อมูลในตัวอย่างนี้ หากลองพิจารณาแนวโน้มดู จะเห็นได้ว่าแม้จะมีขึ้นลงสลับกันไปบ้างแต่โดยรวมแล้วก็คือยิ่งเวลาผ่านไปก็ยิ่งกินจุขึ้น โดยมีแนวโน้มค่อนข้างเป็นเส้นตรงแน่นอน
ดังนั้นจึงควรจะสามารถเขียนสมการอธิบายความสัมพันธ์ระหว่างปริมาณอาหารเทียบกับเวลาได้ดังนี้
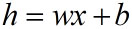
โดยในที่นี้ x เป็นตัวแปรต้น และ h เป็นตัวแปรตาม ส่วน w ในที่นี้เรียกว่าเป็นค่าน้ำหนักของตัวแปรต้น x และ b เรียกว่าเป็นค่าไบแอส
การพยายามวิเคราะห์ว่าค่า w และ b ในที่นี้ควรจะเป็นเท่าไหร่นั่นก็คือปัญหาที่เรียกว่า "การวิเคราะห์การถดถอยเชิงเส้น"
แน่นอนว่าหากแนวโน้มไม่ใช่เส้นตรงแบบนี้ก็ไม่สามารถใช้การถดถอยเชิงเส้นได้ กรณีแบบนั้นก็จะเป็นการถดถอยแบบอื่น ซึ่งก็มีอีกหลากหลายวิธี จะยังไม่กล่าวถึงตรงนี้
การถดถอยเชิงเส้นอาจไม่ได้มีตัวแปรต้นแค่ตัวเดียวแบบนี้ กรณีโจทย์นี้เป็นปัญหาหนึ่งมิติ คือมีตัวแปรต้นตัวเดียวคือ x ดังนั้นจะมีค่า w ที่ต้องหาอยู่แค่ตัวเดียว และมี b อีกตัว
แต่ปัญหาทั่วไปอาจมีตัวแปรต้นหลายตัว ในกรณีแบบนั้นจะเป็น
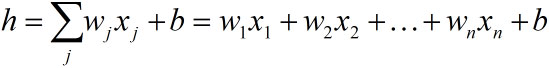
โดย n เป็นจำนวนมิติ (จำนวนตัวแปรต้น) ของปัญหา
แบบนี้จะมีค่าที่ต้องการหาคือ w1, w2, w3,..., wn และ b ปัญหาจะซับซ้อนขึ้นไปอีก
ในเบื้องต้นขอเริ่มจากปัญหาหนึ่งมิติดังในตัวอย่างที่ยกมานี้ก่อน จึงค่อยต่อยอดไปยังมิติที่สูงขึ้น
ก่อนอื่นขอเฉลยว่าผลการทดลองอันนี้ได้มาจากการเขียนโค้ดดังนี้
ซึ่งหากดูก็จะรู้ทันทีว่าคำตอบของปัญหานี้คือ w = 2.5 และ b = 0.5 นั่นเอง โดยมีค่าสุ่มบวกเพิ่มเข้ามาด้วย ซึ่งอาจเกิดจากปัจจัยความไม่แน่นอนที่ไม่สามารถควบคุมได้ เช่น อุณหภูมิและความชื้นในวันนั้นๆ ตรงนี้ถือเป็นคลื่นรบกวน
ปัญหาก็คือจะหาค่า w และ b ในนี้ได้อย่างไรถ้าเราไม่รู้มาก่อนเลย ดูแค่จากรูปเท่านั้น
ถ้าคิดหยาบๆละก็ เราอาจพยายามลองลากเส้นผ่านกลางจุดเหล่านี้แล้วดูว่าเส้นอยู่กึ่งกลางระหว่างจุด แต่ตาคนย่อมมีข้อผิดพลาดไม่อาจกะได้แม่นยำ ดังนั้นจึงต้องทำการคำนวณด้วยคอมพิวเตอร์
ที่จริงคือคำตอบอาจมีอยู่หลากหลายขึ้นอยู่กับเกณฑ์หรือวิธีการที่ใช้
วิธีที่นิยมที่สุดก็คือการพยายามหาค่า w และ b ที่ทำให้คำนวณแล้วได้ค่าความคลาดเคลื่อนต่ำที่สุด
ค่าความคลาดเคลื่อนในที่นี้ที่นิยมใช้ก็คือผลรวมความคลาดเคลื่อนกำลังสอง (和方差, sum of squared error, SSE) หรือค่าเฉลี่ยความคลาดเคลื่อนกำลังสอง (均方差, mean sqared error, MSE)
โดย SSE ได้จากการนำเอาผลต่างระหว่างค่าที่ทำนายกับคำตอบจริงของแต่ละตัวอย่างมายกกำลังสอง แล้วนำมาบวกกันทั้งหมด
กรณีหนึ่งมิติอย่างปัญหานี้จะได้ว่า
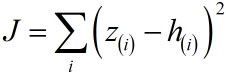
ในที่นี้ใช้ J แทนค่า SSE โดย z คือคำตอบจริง
ส่วน h คือค่าที่ทำนายจากการคำนวณจากตัวแปรต้นคูณน้ำหนักบวกไบแอส นั่นคือ
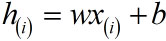
โดย (i) เป็นดัชนีชี้ลำดับแถวของข้อมูล ต้องนำความคลาดเคลื่อนที่คิดจากข้อมูลทั้งหมดมารวมกัน
เขียนในไพธอนได้ว่า
ส่วน MSE ก็ได้จากการนำ SSE มาหารจำนวนตัวอย่าง จะใช้ SSE หรือ MSE ก็ให้ผลไม่ต่างกัน ยังไงเป้าหมายก็คือทำยังไงก็ได้ให้ค่าน้อยที่สุด
เราอาจเริ่มจากเดาค่า w และ b มาหลายๆชุด แล้วดูว่าค่าไหนที่ทำให้คำนวณค่าความคลาดเคลื่อนได้น้อยที่สุด
แต่ทำแบบนั้นก็อาจเหมือนงมเข็มในมหาสมุทร ดังนั้นโดยทั่วไปแทนที่จะทำอย่างนั้น พอสุ่มค่า w และ b มาค่าหนึ่งก็ดูแนวโน้มว่าต่อไปควรจะแก้ค่ายังไงเพื่อให้ความคลาดเคลื่อนลดลง และทำอย่างนี้ต่อไปเรื่อยๆจนไม่น่าจะได้ค่าต่ำไปกว่านี้แล้ว
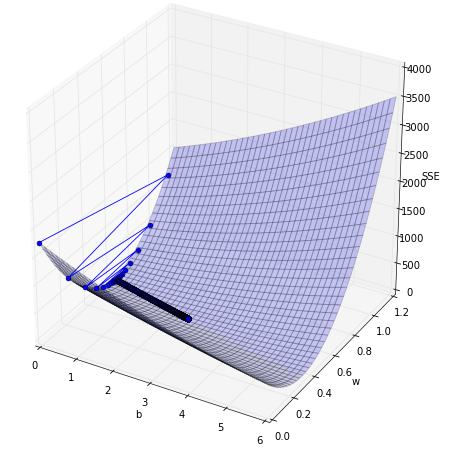
ลองวาดพื้นผิวสามมิติเพื่อแสดงความสัมพันธ์ระหว่าง w, b และ SSE ได้ดังนี้
ax = plt.axes([0,0,1,1],projection='3d',xlabel='b',ylabel='w',zlabel='SSE')
mb,mw = np.meshgrid(np.linspace(0,5,41),np.linspace(0,1,41))
sse = ((x*mw.ravel()[:,None]+mb.ravel()[:,None]-z)**2).sum(1).reshape(41,-1)
ax.plot_surface(mb,mw,sse,rstride=1,cstride=1,alpha=0.2)
plt.show()
ผลที่ได้จะบอกว่าถ้า w และ b เป็นเท่าไหร่ จะได้ค่า SSE เท่าไหร่ โดยจะเห็นลักษณะเหมือนเป็นหุบเขา มีร่องอยู่ตรงกลาง ตำแหน่งของคำตอบที่เราต้องการก็อยู่ในร่องนั่นเอง
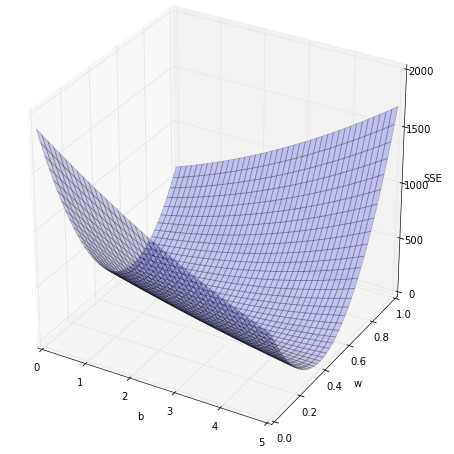
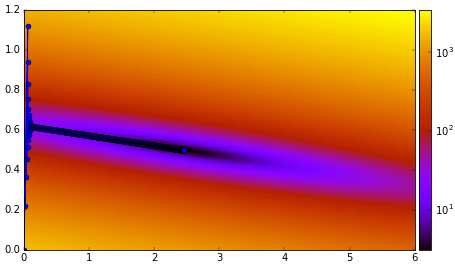
จากรูปนี้ดูเผินๆอาจเหมือนกับว่าภายในร่องนั้นดูจะมีค่าเท่าๆกันไปหมด แต่ความจริงแล้วก็มีความแตกต่างเล็กๆน้อยๆอยู่ เพื่อให้เห็นความต่างเล็กๆน้อยๆได้ง่ายคราวนี้ลองเปลี่ยนเป็นวาดแผนภาพไล่สีแทน โดยสีแสดงถึงความสูง โดยให้แสดงเป็นมาตราส่วนลอการิธึม
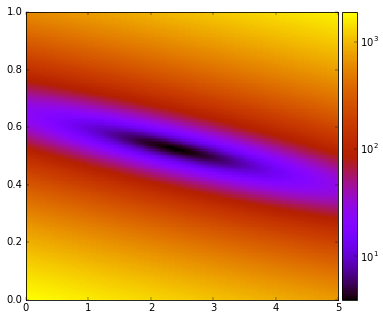
ในรูปนี้สีเหลืองคือค่าสูง สีดำคือค่าต่ำ จะเห็นว่าจุดที่ดำที่สุดก็คือแถว (2.5,0.5) ซึ่งเป็นคำตอบนั่นเอง
หากดูจากรูปเราก็คงพอเข้าใจคร่าวๆได้ว่าคำตอบที่ควรจะเป็นตรงไหน แต่ทีนี้เราจะเขียนโปรแกรมยังไงให้มันหาคำตอบนั้นเจอได้เอง นั่นคือโจทย์ในตอนนี้
วิธีการหาคำตอบนั้นอาจมีอยู่หลายวิธี แต่ในที่นี้จะแนะนำวิธีที่เรียกว่าการเคลื่อนลงตามความชัน (梯度下降法, gradient descent, GD) ซึ่งนิยมใช้มากที่สุด
สมมุติว่าเราทำเข็มอันหนึ่งตกลงไปในมหาสมุทร แต่เรารู้ว่าของมีน้ำหนักย่อมตกสู่ที่ต่ำ ดังนั้นถ้าจะหาเข็มให้เจอเราก็ต้องหาพื้นใต้สมุทรส่วนที่อยู่ต่ำที่สุด
เราอาจเริ่มจากดำน้ำลงจุดไหนสักจุดก่อนแล้วดูว่าจุดนั้นมีความลาดเอียงแค่ไหน ถ้าจุดที่เราดำน้ำลงมาเจอพื้นนั้นไม่ใช่จุดต่ำที่สุดเราก็จะต้องรู้สึกได้ถึงความลาดเอียงของพื้น แล้วก็จะสามารถคิดได้ว่าหากอยากไปที่ที่ต่ำลงไปก็ต้องเคลื่อนที่ไปตามความลาดเอียงนั้น
นั่นคือแนวคิดของเทคนิคการเคลื่อนลงการตามความชันก็คือหาค่าความชันของตำแหน่งที่อยู่ แล้วใช้มันเป็นตัวกำหนดทิศทางว่าจะปรับเปลี่ยนตำแหน่งไปทางไหนต่อ
"ตำแหน่ง" ในที่นี้หมายถึงค่า w และ b ในขณะที่ "ความสูง" คือค่า SSE
"ความชัน" ในที่นี้คืออนุพันธ์ของ SSE โดยคิดเป็นอนุพันธ์ย่อยเทียบกับ w และ b นั่นคือ
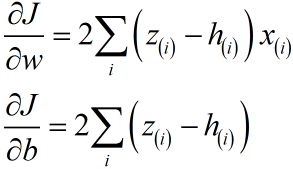
จากนั้นเมื่อคำนวณอนุพันธ์ได้แล้ว ต่อมาก็คำนวณค่าน้ำหนัก w และไบแอส b ที่ควรจะเปลี่ยนได้โดย
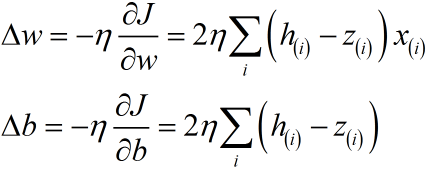
โดย η คือสิ่งที่เรียกว่า "อัตราการเรียนรู้" เป็นค่าที่กำหนดว่าในแต่ละรอบที่มีการปรับค่าน้ำหนักและไบแอสจะปรับมากแค่ไหน
ค่านี้มีความสำคัญมากต้องกำหนดให้เหมาะกับปัญหา ถ้ามากเกินไปน้ำหนักจะถูกปรับมากเกินจนไม่อาจลู่เข้าสู่คำตอบได้ แต่ถ้าน้อยไปการปรับน้ำหนักก็จะแทบไม่คืบหน้า เรื่องนี้เดี๋ยวจะแสดงให้เห็นต่อไป
ตอนนี้ได้สมการมาแล้ว ดังนั้นลองเริ่มเขียนโค้ด
เมื่อรันโปรแกรมก็จะมีการทำซ้ำหมื่นครั้งเพื่อเรียนรู้และปรับค่า w และ b ไปเรื่อยๆเพื่อให้เข้าใกล้คำตอบที่ต้องการ หากการเรียนรู้ถูกทำอย่างถูกต้องเมื่อสิ้นสุดลงค่า w และ b ก็ควรจะเป็นไปอย่างที่ควรจะเป็น
ลองนำค่า w และ b ที่ได้ท้ายที่สุดมาวาดกราฟเส้นตรงเทียบกับจุดดู
จะเห็นว่าคำตอบออกมาอย่างที่ควรจะเป็น
เพื่อให้เห็นความคืบหน้าในการเรียนรู้แต่ละครั้งชัดเจนลองนำค่า w และ b ที่เก็บไว้ในลิสต์ wi และ bi ตอนแรกมาวาดกราฟเทียบกับระนาบของค่า SSE ดู ทั้งภาพสามมิติและแผนภาพไล่สี
จะเห็นว่าเส้นทางค่อยๆไต่ลงสู่พื้นที่ต่ำลงเรื่อยๆ โดยเคลื่อนลงสู่ร่องหุบเขาก่อนอย่างรวดเร็ว จากนั้นยังเคลื่อนที่ภายในร่องต่อ การเคลื่อนที่ในร่องจะเป็นไปอย่างช้าเพราะความต่างของความชันภายในร่องค่อนข้างต่ำ แต่สุดท้ายก็จะลงสู่ส่วนลึกสุดภายในร่อง
จำนวนครั้งที่ทำซ้ำนั้นยิ่งเยอะก็ยิ่งทำให้ค่าเข้าใกล้ส่วนต่ำสุด แต่ยิ่งเข้าใกล้อัตราการเปลี่ยนแปลงก็จะยิ่งลดลง เราอาจจะเขียนโปรแกรมโดยกำหนดให้ทำซ้ำจนกว่าการเปลี่ยนแปลงจะน้อยจนถึงค่าหนึ่งแทนที่จะกำหนดเป็นจำนวนที่ทำซ้ำก็ได้
เราอาจกำหนดเกณฑ์ในการให้หยุดโดยให้หยุดเมื่อค่า SSE เปลี่ยนแปลงน้อยมากก็ได้ แต่ในที่นี้จะใช้การเปลี่ยนแปลงค่า w และ b เป็นตัวกำหนด
เช่น ลองกำหนดให้หยุดเมื่อทั้งค่า w และ b เปลี่ยนแปลงน้อยกว่า 0.0000001 จะเขียนได้แบบนี้
ที่ยังต้องกำหนดจำนวนครั้งสูงสุดไว้ก็เผื่อว่าคำตอบจะไม่ลู่เข้า แบบนั้นก็จะกลายเป็นวนทำซ้ำไปเรื่อยๆไม่มีที่สิ้นสุด
เพราะไม่ใช่ว่าการเรียนรู้จะราบรื่นเสมอไป บางทีคำตอบอาจไม่ได้ลู่เข้าก็เป็นได้ เช่นกรณีที่กำหนดค่าอัตราการเรียนรู้สูงเกินไป
เช่น ลองใช้โจทย์ข้อเดิมแต่ปรับ eta ให้สูงขึ้น แล้วลองทำซ้ำดูแค่ ๑๐ ครั้ง จากนั้นดูค่า w, b และ SSE ที่เปลี่ยนแปลงไป
จะเห็นว่าคราวนี้ยิ่งทำซ้ำไปค่าก็ยิ่งสูงขึ้น (ภาพนี้จุดเริ่มต้นอยู่ด้านล่างสุด ไม่ใช่ด้านบน)
ที่เป็นแบบนี้ก็เพราะพออัตราการเรียนรู้สูงเกินไปพอปรับค่าน้ำหนักไปทีหนึ่งก็โดดแรงไปจนข้ามร่องไปยังส่วนที่สูงขึ้นของฝั่งตรงข้าม ยิ่งปรับยิ่งโดดข้ามไปข้ามมาจนสูงขึ้นเรื่อยๆแทนที่จะลดลง
ดังนั้นการกำหนดอัตราการเรียนรู้ให้ต่ำเอาไว้อาจปลอดภัยกว่า แต่ก็ทำให้จำนวนครั้งที่ทำซ้ำมากขึ้นตาม ต้องใช้เวลานานในการเข้าถึงคำตอบ
ในเทคนิคการเคลื่อนลงตามความชันแบบธรรมดาดั้งเดิม อัตราการเรียนรู้จะเป็นค่าคงที่ตลอดการเรียนรู้ แต่ปัจจุบันมีคนคิดวิธีการที่ปรับปรุงขึ้นมามากมาย เช่น AdaGrad, AdaDelta, Adam, ฯลฯ ซึ่งก็มีพื้นฐานเหมือนกันคือต้องคำนวณค่าความชันเพื่อปรับค่าน้ำหนักและไบแอส แต่ต่างกันที่ว่าอัตราการเรียนรู้จะเปลี่ยนแปลงไปเรื่อยๆ โดยอาศัยวิธีคิดต่างๆ
รายละเอียดตรงนี้จะยังไม่พูดถึง การปรับปรุงวิธีการเคลื่อนลงตามความชันอาจเขียนถึงในโอกาสหน้า
เท่านี้ก็พอจะสามารถแก้ปัญหาการถดถอยเชิงเส้นแบบหนึ่งมิติได้แล้ว ตอนต่อไปจะเขียนต่อยอดไปเป็นการแก้ปัญหาการถดถอยเชิงเส้นแบบหลายมิติต่อไป อ่านต่อได้ใน https://phyblas.hinaboshi.com/20161212
อ้างอิง
ศาสตร์นี้มีเรื่องที่น่าเขียนถึงอยู่หลายอย่าง แต่ที่น่าพูดถึงมากที่สุดที่อยากเขียนถึงก็คือการวิเคราะห์การถดถอยโลจิสติก (逻辑回归, logistic regression) และการวิเคราะห์การถดถอยเชิงเส้น (线性回归, linear regression) ซึ่งใช้งานอย่างกว้างขวางและสามารถต่อยอดไปสู่เทคนิคอื่นๆที่ซับซ้อนขึ้นเช่นการสร้างระบบโครงข่ายประสาทได้
ก่อนหน้านี้ได้มีเขียนบทความแรกคือเรื่องการวิเคราะห์ถดถอยโลจิสติกไปแล้วใน https://phyblas.hinaboshi.com/20161103
แต่ในนั้นได้ข้ามรายละเอียดอะไรที่ควรเขียนถึงไปหลายอย่าง ที่สำคัญที่สุดอย่างหนึ่งก็คือ แต่ไหนแต่ไรแล้ว "การวิเคราะห์การถดถอย" หมายถึงอะไร
ดังนั้นในบทความนี้จะพูดถึงความหมายของการวิเคราะห์ถดถอย พร้อมทั้งทดลองเขียนโค้ดการวิเคราะห์ถดถอยอย่างง่ายสุด นั่นคือการวิเคราะห์ถดถอยแบบเชิงเส้น
การถดถอยเชิงเส้นนั้นนอกจากจะเป็นการถดถอยแบบง่ายที่สุดแล้ว ยังถูกนำไปต่อยอดเพื่อทำอะไรต่างๆได้มาก เช่นการวิเคราะห์การถดถอยโลจิสติกเพื่อการแบ่งกลุ่มข้อมูลนั้นที่จริงแล้วก็มีพื้นฐานอยู่บนการถดถอยเชิงเส้น
สำหรับใครที่อ่านบทความเรื่องการวิเคราะห์การถดถอยโลจิสติกอันนั้นไปก่อนแล้วจะลืมไปก่อนก็ได้ บทความในหน้านี้ไม่ได้ยืนพื้นจากบทความนั้น ในทางตรงกันข้าม แนะนำให้อ่านหน้านี้ก่อนแล้วค่อยไปอ่านตรงนั้นจะดีกว่า
การวิเคราะห์การถดถอยคืออะไร? อธิบายด้วยคำพูดทันทีอาจเข้าใจยาก ดังนั้นขอเริ่มด้วยการยกตัวอย่างสถานการณ์ที่สามารถใช้เพื่อแก้ปัญหาได้
โจทย์คือ สมมุติว่าซื้อลูกไดโนเสาร์มาตัวหนึ่ง เริ่มเลี้ยงมันตั้งแต่วันแรกที่ซื้อมา ในแต่ละวันไดโนเสาร์จะกินอาหารไปแค่ปริมาณหนึ่งแล้วก็อิ่ม
พอลองจดบันทึกปริมาณอาหารที่มันกินในแต่ละวันโดยบันทึกวันเว้นวันเป็นเวลาเดือนหนึ่งก็ได้ผลออกมาตามนี้

โดยแกนนอนคือเวลาในหน่วยวัน ส่วนแกนตั้งคือน้ำหนักของอาหารที่ต้องให้ในหน่วยกิโลกรัม
คำถามคือพอเห็นแนวโน้มแบบนี้แล้วเราสามารถทำนายได้หรือไม่ว่าวันถัดไปไดโนเสาร์จะกินอาหารกี่ กก.?
อีกทั้งในนี้เรามีการจดบันทึกแค่วันเว้นวัน เราจะบอกได้หรือไม่ว่าวันที่เราไม่ได้จดบันทึกนั้นมันกินอาหารไปกี่ กก.?
การหาคำตอบของปัญหาเหล่านี้ นั่นก็คือสิ่งที่เรียกว่าการวิเคราะห์การถดถอย
การวิเคราะห์การถดถอยก็คือ การวิเคราะห์หาความสัมพันธ์ระหว่างตัวแปรต้นกับตัวแปรตาม โดยวิเคราะห์จากข้อมูลที่มีอยู่โดยดูแนวโน้มต่างๆ แล้วทำนายว่าถ้าตัวแปรต้นมีค่าเท่านี้ ตัวแปรตามจะมีค่าเท่าใด
เช่นโจทย์ข้อนี้ ตัวแปรต้นคือเวลา (เดือน) ตัวแปรตามคือน้ำหนักอาหาร (กก.) เราต้องการทำนายว่าในวันไหนไดโนเสาร์จะกินอาหารเท่าไหร่
สำหรับข้อมูลในตัวอย่างนี้ หากลองพิจารณาแนวโน้มดู จะเห็นได้ว่าแม้จะมีขึ้นลงสลับกันไปบ้างแต่โดยรวมแล้วก็คือยิ่งเวลาผ่านไปก็ยิ่งกินจุขึ้น โดยมีแนวโน้มค่อนข้างเป็นเส้นตรงแน่นอน
ดังนั้นจึงควรจะสามารถเขียนสมการอธิบายความสัมพันธ์ระหว่างปริมาณอาหารเทียบกับเวลาได้ดังนี้
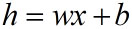
โดยในที่นี้ x เป็นตัวแปรต้น และ h เป็นตัวแปรตาม ส่วน w ในที่นี้เรียกว่าเป็นค่าน้ำหนักของตัวแปรต้น x และ b เรียกว่าเป็นค่าไบแอส
การพยายามวิเคราะห์ว่าค่า w และ b ในที่นี้ควรจะเป็นเท่าไหร่นั่นก็คือปัญหาที่เรียกว่า "การวิเคราะห์การถดถอยเชิงเส้น"
แน่นอนว่าหากแนวโน้มไม่ใช่เส้นตรงแบบนี้ก็ไม่สามารถใช้การถดถอยเชิงเส้นได้ กรณีแบบนั้นก็จะเป็นการถดถอยแบบอื่น ซึ่งก็มีอีกหลากหลายวิธี จะยังไม่กล่าวถึงตรงนี้
การถดถอยเชิงเส้นอาจไม่ได้มีตัวแปรต้นแค่ตัวเดียวแบบนี้ กรณีโจทย์นี้เป็นปัญหาหนึ่งมิติ คือมีตัวแปรต้นตัวเดียวคือ x ดังนั้นจะมีค่า w ที่ต้องหาอยู่แค่ตัวเดียว และมี b อีกตัว
แต่ปัญหาทั่วไปอาจมีตัวแปรต้นหลายตัว ในกรณีแบบนั้นจะเป็น
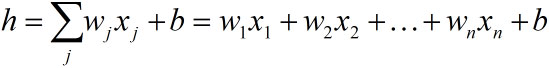
โดย n เป็นจำนวนมิติ (จำนวนตัวแปรต้น) ของปัญหา
แบบนี้จะมีค่าที่ต้องการหาคือ w1, w2, w3,..., wn และ b ปัญหาจะซับซ้อนขึ้นไปอีก
ในเบื้องต้นขอเริ่มจากปัญหาหนึ่งมิติดังในตัวอย่างที่ยกมานี้ก่อน จึงค่อยต่อยอดไปยังมิติที่สูงขึ้น
ก่อนอื่นขอเฉลยว่าผลการทดลองอันนี้ได้มาจากการเขียนโค้ดดังนี้
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(1,31,2)
z = 2.5+x*0.5+np.random.randn(15)*0.5
plt.axes(xlim=[0,31])
plt.xlabel(u'เวลา (วัน)',fontname='Tahoma')
plt.ylabel(u'ปริมาณอาหาร (กก.)',fontname='Tahoma')
plt.scatter(x,z)
plt.show()
import matplotlib.pyplot as plt
x = np.arange(1,31,2)
z = 2.5+x*0.5+np.random.randn(15)*0.5
plt.axes(xlim=[0,31])
plt.xlabel(u'เวลา (วัน)',fontname='Tahoma')
plt.ylabel(u'ปริมาณอาหาร (กก.)',fontname='Tahoma')
plt.scatter(x,z)
plt.show()
ซึ่งหากดูก็จะรู้ทันทีว่าคำตอบของปัญหานี้คือ w = 2.5 และ b = 0.5 นั่นเอง โดยมีค่าสุ่มบวกเพิ่มเข้ามาด้วย ซึ่งอาจเกิดจากปัจจัยความไม่แน่นอนที่ไม่สามารถควบคุมได้ เช่น อุณหภูมิและความชื้นในวันนั้นๆ ตรงนี้ถือเป็นคลื่นรบกวน
ปัญหาก็คือจะหาค่า w และ b ในนี้ได้อย่างไรถ้าเราไม่รู้มาก่อนเลย ดูแค่จากรูปเท่านั้น
ถ้าคิดหยาบๆละก็ เราอาจพยายามลองลากเส้นผ่านกลางจุดเหล่านี้แล้วดูว่าเส้นอยู่กึ่งกลางระหว่างจุด แต่ตาคนย่อมมีข้อผิดพลาดไม่อาจกะได้แม่นยำ ดังนั้นจึงต้องทำการคำนวณด้วยคอมพิวเตอร์
ที่จริงคือคำตอบอาจมีอยู่หลากหลายขึ้นอยู่กับเกณฑ์หรือวิธีการที่ใช้
วิธีที่นิยมที่สุดก็คือการพยายามหาค่า w และ b ที่ทำให้คำนวณแล้วได้ค่าความคลาดเคลื่อนต่ำที่สุด
ค่าความคลาดเคลื่อนในที่นี้ที่นิยมใช้ก็คือผลรวมความคลาดเคลื่อนกำลังสอง (和方差, sum of squared error, SSE) หรือค่าเฉลี่ยความคลาดเคลื่อนกำลังสอง (均方差, mean sqared error, MSE)
โดย SSE ได้จากการนำเอาผลต่างระหว่างค่าที่ทำนายกับคำตอบจริงของแต่ละตัวอย่างมายกกำลังสอง แล้วนำมาบวกกันทั้งหมด
กรณีหนึ่งมิติอย่างปัญหานี้จะได้ว่า
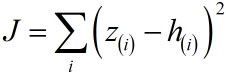
ในที่นี้ใช้ J แทนค่า SSE โดย z คือคำตอบจริง
ส่วน h คือค่าที่ทำนายจากการคำนวณจากตัวแปรต้นคูณน้ำหนักบวกไบแอส นั่นคือ
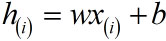
โดย (i) เป็นดัชนีชี้ลำดับแถวของข้อมูล ต้องนำความคลาดเคลื่อนที่คิดจากข้อมูลทั้งหมดมารวมกัน
เขียนในไพธอนได้ว่า
h = w*x+b
sse = ((z-h)**2).sum()
sse = ((z-h)**2).sum()
ส่วน MSE ก็ได้จากการนำ SSE มาหารจำนวนตัวอย่าง จะใช้ SSE หรือ MSE ก็ให้ผลไม่ต่างกัน ยังไงเป้าหมายก็คือทำยังไงก็ได้ให้ค่าน้อยที่สุด
เราอาจเริ่มจากเดาค่า w และ b มาหลายๆชุด แล้วดูว่าค่าไหนที่ทำให้คำนวณค่าความคลาดเคลื่อนได้น้อยที่สุด
แต่ทำแบบนั้นก็อาจเหมือนงมเข็มในมหาสมุทร ดังนั้นโดยทั่วไปแทนที่จะทำอย่างนั้น พอสุ่มค่า w และ b มาค่าหนึ่งก็ดูแนวโน้มว่าต่อไปควรจะแก้ค่ายังไงเพื่อให้ความคลาดเคลื่อนลดลง และทำอย่างนี้ต่อไปเรื่อยๆจนไม่น่าจะได้ค่าต่ำไปกว่านี้แล้ว
ลองวาดพื้นผิวสามมิติเพื่อแสดงความสัมพันธ์ระหว่าง w, b และ SSE ได้ดังนี้
from mpl_toolkits.mplot3d import Axes3D
plt.figure(figsize=[8,8])ax = plt.axes([0,0,1,1],projection='3d',xlabel='b',ylabel='w',zlabel='SSE')
mb,mw = np.meshgrid(np.linspace(0,5,41),np.linspace(0,1,41))
sse = ((x*mw.ravel()[:,None]+mb.ravel()[:,None]-z)**2).sum(1).reshape(41,-1)
ax.plot_surface(mb,mw,sse,rstride=1,cstride=1,alpha=0.2)
plt.show()

ผลที่ได้จะบอกว่าถ้า w และ b เป็นเท่าไหร่ จะได้ค่า SSE เท่าไหร่ โดยจะเห็นลักษณะเหมือนเป็นหุบเขา มีร่องอยู่ตรงกลาง ตำแหน่งของคำตอบที่เราต้องการก็อยู่ในร่องนั่นเอง
จากรูปนี้ดูเผินๆอาจเหมือนกับว่าภายในร่องนั้นดูจะมีค่าเท่าๆกันไปหมด แต่ความจริงแล้วก็มีความแตกต่างเล็กๆน้อยๆอยู่ เพื่อให้เห็นความต่างเล็กๆน้อยๆได้ง่ายคราวนี้ลองเปลี่ยนเป็นวาดแผนภาพไล่สีแทน โดยสีแสดงถึงความสูง โดยให้แสดงเป็นมาตราส่วนลอการิธึม
import matplotlib as mpl
mb,mw = np.meshgrid(np.linspace(0,5,201),np.linspace(0,1,201))
sse = ((x*mw.ravel()[:,None]+mb.ravel()[:,None]-z)**2).sum(1).reshape(201,-1)
plt.axes(xlim=[0,5],ylim=[0,1])
plt.pcolormesh(mb,mw,sse,norm=mpl.colors.LogNorm(),cmap='gnuplot')
plt.colorbar(pad=0.01)
plt.show()
mb,mw = np.meshgrid(np.linspace(0,5,201),np.linspace(0,1,201))
sse = ((x*mw.ravel()[:,None]+mb.ravel()[:,None]-z)**2).sum(1).reshape(201,-1)
plt.axes(xlim=[0,5],ylim=[0,1])
plt.pcolormesh(mb,mw,sse,norm=mpl.colors.LogNorm(),cmap='gnuplot')
plt.colorbar(pad=0.01)
plt.show()

ในรูปนี้สีเหลืองคือค่าสูง สีดำคือค่าต่ำ จะเห็นว่าจุดที่ดำที่สุดก็คือแถว (2.5,0.5) ซึ่งเป็นคำตอบนั่นเอง
หากดูจากรูปเราก็คงพอเข้าใจคร่าวๆได้ว่าคำตอบที่ควรจะเป็นตรงไหน แต่ทีนี้เราจะเขียนโปรแกรมยังไงให้มันหาคำตอบนั้นเจอได้เอง นั่นคือโจทย์ในตอนนี้
วิธีการหาคำตอบนั้นอาจมีอยู่หลายวิธี แต่ในที่นี้จะแนะนำวิธีที่เรียกว่าการเคลื่อนลงตามความชัน (梯度下降法, gradient descent, GD) ซึ่งนิยมใช้มากที่สุด
สมมุติว่าเราทำเข็มอันหนึ่งตกลงไปในมหาสมุทร แต่เรารู้ว่าของมีน้ำหนักย่อมตกสู่ที่ต่ำ ดังนั้นถ้าจะหาเข็มให้เจอเราก็ต้องหาพื้นใต้สมุทรส่วนที่อยู่ต่ำที่สุด
เราอาจเริ่มจากดำน้ำลงจุดไหนสักจุดก่อนแล้วดูว่าจุดนั้นมีความลาดเอียงแค่ไหน ถ้าจุดที่เราดำน้ำลงมาเจอพื้นนั้นไม่ใช่จุดต่ำที่สุดเราก็จะต้องรู้สึกได้ถึงความลาดเอียงของพื้น แล้วก็จะสามารถคิดได้ว่าหากอยากไปที่ที่ต่ำลงไปก็ต้องเคลื่อนที่ไปตามความลาดเอียงนั้น
นั่นคือแนวคิดของเทคนิคการเคลื่อนลงการตามความชันก็คือหาค่าความชันของตำแหน่งที่อยู่ แล้วใช้มันเป็นตัวกำหนดทิศทางว่าจะปรับเปลี่ยนตำแหน่งไปทางไหนต่อ
"ตำแหน่ง" ในที่นี้หมายถึงค่า w และ b ในขณะที่ "ความสูง" คือค่า SSE
"ความชัน" ในที่นี้คืออนุพันธ์ของ SSE โดยคิดเป็นอนุพันธ์ย่อยเทียบกับ w และ b นั่นคือ
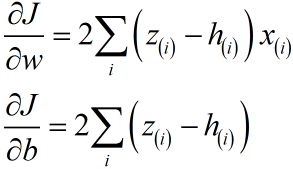
จากนั้นเมื่อคำนวณอนุพันธ์ได้แล้ว ต่อมาก็คำนวณค่าน้ำหนัก w และไบแอส b ที่ควรจะเปลี่ยนได้โดย
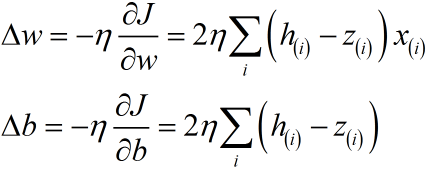
โดย η คือสิ่งที่เรียกว่า "อัตราการเรียนรู้" เป็นค่าที่กำหนดว่าในแต่ละรอบที่มีการปรับค่าน้ำหนักและไบแอสจะปรับมากแค่ไหน
ค่านี้มีความสำคัญมากต้องกำหนดให้เหมาะกับปัญหา ถ้ามากเกินไปน้ำหนักจะถูกปรับมากเกินจนไม่อาจลู่เข้าสู่คำตอบได้ แต่ถ้าน้อยไปการปรับน้ำหนักก็จะแทบไม่คืบหน้า เรื่องนี้เดี๋ยวจะแสดงให้เห็นต่อไป
ตอนนี้ได้สมการมาแล้ว ดังนั้นลองเริ่มเขียนโค้ด
eta = 0.0002 # อัตราการเรียนรู้
n_thamsam = 10000 # จำนวนครั้งที่ทำซ้ำเพื่อเรียนรู้
w,b = 0,0 # น้ำหนักและไบแอสเริ่มต้น
wi = [w] # ลิสต์บันทึกค่าน้ำหนักและไบแอส
bi = [b]
h = w*x+b # คำนวณคำตอบโดยใช้ w และ b ตอนแรก
for i in range(n_thamsam):
w += 2*((z-h)*x).sum()*eta # ปรับค่าน้ำหนักและไบแอส
b += 2*(z-h).sum()*eta
wi += [w] # บันทึกค่าน้ำหนักและไบแอสใหม่
bi += [b]
h = w*x+b # คำนวณคำตอบโดยใช้ค่า w และ b ใหม่
n_thamsam = 10000 # จำนวนครั้งที่ทำซ้ำเพื่อเรียนรู้
w,b = 0,0 # น้ำหนักและไบแอสเริ่มต้น
wi = [w] # ลิสต์บันทึกค่าน้ำหนักและไบแอส
bi = [b]
h = w*x+b # คำนวณคำตอบโดยใช้ w และ b ตอนแรก
for i in range(n_thamsam):
w += 2*((z-h)*x).sum()*eta # ปรับค่าน้ำหนักและไบแอส
b += 2*(z-h).sum()*eta
wi += [w] # บันทึกค่าน้ำหนักและไบแอสใหม่
bi += [b]
h = w*x+b # คำนวณคำตอบโดยใช้ค่า w และ b ใหม่
เมื่อรันโปรแกรมก็จะมีการทำซ้ำหมื่นครั้งเพื่อเรียนรู้และปรับค่า w และ b ไปเรื่อยๆเพื่อให้เข้าใกล้คำตอบที่ต้องการ หากการเรียนรู้ถูกทำอย่างถูกต้องเมื่อสิ้นสุดลงค่า w และ b ก็ควรจะเป็นไปอย่างที่ควรจะเป็น
ลองนำค่า w และ b ที่ได้ท้ายที่สุดมาวาดกราฟเส้นตรงเทียบกับจุดดู
plt.axes(xlim=[0,31])
plt.xlabel(u'เวลา (วัน)',fontname='Tahoma')
plt.ylabel(u'ปริมาณอาหาร (กก.)',fontname='Tahoma')
plt.scatter(x,z)
xsen = np.array([0,31])
ysen = xsen*w+b
plt.plot(xsen,ysen,'b')
plt.show()
plt.xlabel(u'เวลา (วัน)',fontname='Tahoma')
plt.ylabel(u'ปริมาณอาหาร (กก.)',fontname='Tahoma')
plt.scatter(x,z)
xsen = np.array([0,31])
ysen = xsen*w+b
plt.plot(xsen,ysen,'b')
plt.show()
จะเห็นว่าคำตอบออกมาอย่างที่ควรจะเป็น

เพื่อให้เห็นความคืบหน้าในการเรียนรู้แต่ละครั้งชัดเจนลองนำค่า w และ b ที่เก็บไว้ในลิสต์ wi และ bi ตอนแรกมาวาดกราฟเทียบกับระนาบของค่า SSE ดู ทั้งภาพสามมิติและแผนภาพไล่สี
bi = np.array(bi)
wi = np.array(wi)
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d',xlabel='b',ylabel='w',zlabel='SSE')
ssei = ((x*wi[:,None]+bi[:,None]-z)**2).sum(1)
ax.plot(bi,wi,ssei,'bo-')
mb,mw = np.meshgrid(np.linspace(0,3,201),np.linspace(0,1.2,201))
sse = ((x*mw.ravel()[:,None]+mb.ravel()[:,None]-z)**2).sum(1).reshape(201,-1)
ax.plot_surface(mb,mw,sse,rstride=5,cstride=5,alpha=0.2,color='b',edgecolor='k')
plt.figure(figsize=[10,5])
plt.pcolormesh(mb,mw,sse,norm=mpl.colors.LogNorm(),cmap='gnuplot')
plt.colorbar(pad=0.01)
plt.plot(bi,wi,'bo-')
plt.show()
wi = np.array(wi)
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d',xlabel='b',ylabel='w',zlabel='SSE')
ssei = ((x*wi[:,None]+bi[:,None]-z)**2).sum(1)
ax.plot(bi,wi,ssei,'bo-')
mb,mw = np.meshgrid(np.linspace(0,3,201),np.linspace(0,1.2,201))
sse = ((x*mw.ravel()[:,None]+mb.ravel()[:,None]-z)**2).sum(1).reshape(201,-1)
ax.plot_surface(mb,mw,sse,rstride=5,cstride=5,alpha=0.2,color='b',edgecolor='k')
plt.figure(figsize=[10,5])
plt.pcolormesh(mb,mw,sse,norm=mpl.colors.LogNorm(),cmap='gnuplot')
plt.colorbar(pad=0.01)
plt.plot(bi,wi,'bo-')
plt.show()


จะเห็นว่าเส้นทางค่อยๆไต่ลงสู่พื้นที่ต่ำลงเรื่อยๆ โดยเคลื่อนลงสู่ร่องหุบเขาก่อนอย่างรวดเร็ว จากนั้นยังเคลื่อนที่ภายในร่องต่อ การเคลื่อนที่ในร่องจะเป็นไปอย่างช้าเพราะความต่างของความชันภายในร่องค่อนข้างต่ำ แต่สุดท้ายก็จะลงสู่ส่วนลึกสุดภายในร่อง
จำนวนครั้งที่ทำซ้ำนั้นยิ่งเยอะก็ยิ่งทำให้ค่าเข้าใกล้ส่วนต่ำสุด แต่ยิ่งเข้าใกล้อัตราการเปลี่ยนแปลงก็จะยิ่งลดลง เราอาจจะเขียนโปรแกรมโดยกำหนดให้ทำซ้ำจนกว่าการเปลี่ยนแปลงจะน้อยจนถึงค่าหนึ่งแทนที่จะกำหนดเป็นจำนวนที่ทำซ้ำก็ได้
เราอาจกำหนดเกณฑ์ในการให้หยุดโดยให้หยุดเมื่อค่า SSE เปลี่ยนแปลงน้อยมากก็ได้ แต่ในที่นี้จะใช้การเปลี่ยนแปลงค่า w และ b เป็นตัวกำหนด
เช่น ลองกำหนดให้หยุดเมื่อทั้งค่า w และ b เปลี่ยนแปลงน้อยกว่า 0.0000001 จะเขียนได้แบบนี้
eta = 0.0002
n_thamsam = 100000
d_yut = 1e-7 # ค่าความเปลี่ยนแปลงน้ำหนักและไบแอสสูงสุดที่จะให้หยุดได้
w,b = 0,0
h = w*x+b
for i in range(n_thamsam):
dw = 2*((z-h)*x).sum()*eta
db = 2*(z-h).sum()*eta
w += dw
b += db
h = w*x+b
if(np.abs(dw)and np.abs(db)<d_yut):
break # หยุดเมื่อทั้ง dw และ db ต่ำกว่า d_yut
print('ทำซ้ำไป %d ครั้ง dw=%.3e, db=%.3e'%(i,dw,db))
# ทำซ้ำไป 7064 ครั้ง dw=-5.006e-09, db=9.993e-08
n_thamsam = 100000
d_yut = 1e-7 # ค่าความเปลี่ยนแปลงน้ำหนักและไบแอสสูงสุดที่จะให้หยุดได้
w,b = 0,0
h = w*x+b
for i in range(n_thamsam):
dw = 2*((z-h)*x).sum()*eta
db = 2*(z-h).sum()*eta
w += dw
b += db
h = w*x+b
if(np.abs(dw)and np.abs(db)<d_yut):
break # หยุดเมื่อทั้ง dw และ db ต่ำกว่า d_yut
print('ทำซ้ำไป %d ครั้ง dw=%.3e, db=%.3e'%(i,dw,db))
# ทำซ้ำไป 7064 ครั้ง dw=-5.006e-09, db=9.993e-08
ที่ยังต้องกำหนดจำนวนครั้งสูงสุดไว้ก็เผื่อว่าคำตอบจะไม่ลู่เข้า แบบนั้นก็จะกลายเป็นวนทำซ้ำไปเรื่อยๆไม่มีที่สิ้นสุด
เพราะไม่ใช่ว่าการเรียนรู้จะราบรื่นเสมอไป บางทีคำตอบอาจไม่ได้ลู่เข้าก็เป็นได้ เช่นกรณีที่กำหนดค่าอัตราการเรียนรู้สูงเกินไป
เช่น ลองใช้โจทย์ข้อเดิมแต่ปรับ eta ให้สูงขึ้น แล้วลองทำซ้ำดูแค่ ๑๐ ครั้ง จากนั้นดูค่า w, b และ SSE ที่เปลี่ยนแปลงไป
eta = 0.0003
n_thamsam = 10
w,b = 0,0
wi = [w]
bi = [b]
h = w*x+b
for i in range(n_thamsam):
w += 2*((z-h)*x).sum()*eta
b += 2*(z-h).sum()*eta
wi += [w]
bi += [b]
h = w*x+b
bi = np.array(bi)
wi = np.array(wi)
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d',xlabel='b',ylabel='w',zlabel='SSE')
ssei = ((x*wi[:,None]+bi[:,None]-z)**2).sum(1)
ax.plot(bi,wi,ssei,'bo-')
mb,mw = np.meshgrid(np.linspace(bi.min(),bi.max(),201),np.linspace(wi.min(),wi.max(),201))
sse = ((x*mw.ravel()[:,None]+mb.ravel()[:,None]-z)**2).sum(1).reshape(201,-1)
ax.plot_surface(mb,mw,sse,rstride=5,cstride=5,alpha=0.2,color='b',edgecolor='k')
plt.show()
n_thamsam = 10
w,b = 0,0
wi = [w]
bi = [b]
h = w*x+b
for i in range(n_thamsam):
w += 2*((z-h)*x).sum()*eta
b += 2*(z-h).sum()*eta
wi += [w]
bi += [b]
h = w*x+b
bi = np.array(bi)
wi = np.array(wi)
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d',xlabel='b',ylabel='w',zlabel='SSE')
ssei = ((x*wi[:,None]+bi[:,None]-z)**2).sum(1)
ax.plot(bi,wi,ssei,'bo-')
mb,mw = np.meshgrid(np.linspace(bi.min(),bi.max(),201),np.linspace(wi.min(),wi.max(),201))
sse = ((x*mw.ravel()[:,None]+mb.ravel()[:,None]-z)**2).sum(1).reshape(201,-1)
ax.plot_surface(mb,mw,sse,rstride=5,cstride=5,alpha=0.2,color='b',edgecolor='k')
plt.show()

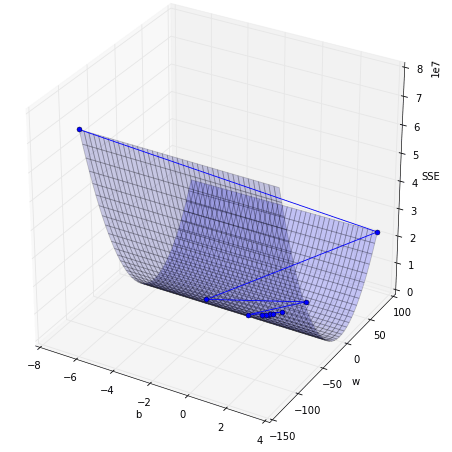
จะเห็นว่าคราวนี้ยิ่งทำซ้ำไปค่าก็ยิ่งสูงขึ้น (ภาพนี้จุดเริ่มต้นอยู่ด้านล่างสุด ไม่ใช่ด้านบน)
ที่เป็นแบบนี้ก็เพราะพออัตราการเรียนรู้สูงเกินไปพอปรับค่าน้ำหนักไปทีหนึ่งก็โดดแรงไปจนข้ามร่องไปยังส่วนที่สูงขึ้นของฝั่งตรงข้าม ยิ่งปรับยิ่งโดดข้ามไปข้ามมาจนสูงขึ้นเรื่อยๆแทนที่จะลดลง
ดังนั้นการกำหนดอัตราการเรียนรู้ให้ต่ำเอาไว้อาจปลอดภัยกว่า แต่ก็ทำให้จำนวนครั้งที่ทำซ้ำมากขึ้นตาม ต้องใช้เวลานานในการเข้าถึงคำตอบ
ในเทคนิคการเคลื่อนลงตามความชันแบบธรรมดาดั้งเดิม อัตราการเรียนรู้จะเป็นค่าคงที่ตลอดการเรียนรู้ แต่ปัจจุบันมีคนคิดวิธีการที่ปรับปรุงขึ้นมามากมาย เช่น AdaGrad, AdaDelta, Adam, ฯลฯ ซึ่งก็มีพื้นฐานเหมือนกันคือต้องคำนวณค่าความชันเพื่อปรับค่าน้ำหนักและไบแอส แต่ต่างกันที่ว่าอัตราการเรียนรู้จะเปลี่ยนแปลงไปเรื่อยๆ โดยอาศัยวิธีคิดต่างๆ
รายละเอียดตรงนี้จะยังไม่พูดถึง การปรับปรุงวิธีการเคลื่อนลงตามความชันอาจเขียนถึงในโอกาสหน้า
เท่านี้ก็พอจะสามารถแก้ปัญหาการถดถอยเชิงเส้นแบบหนึ่งมิติได้แล้ว ตอนต่อไปจะเขียนต่อยอดไปเป็นการแก้ปัญหาการถดถอยเชิงเส้นแบบหลายมิติต่อไป อ่านต่อได้ใน https://phyblas.hinaboshi.com/20161212
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib