[python] วิเคราะห์การถดถอยเชิงเส้นแบบหลายตัวแปร
เขียนเมื่อ 2016/12/12 12:57
แก้ไขล่าสุด 2022/07/21 15:29
ต่อจากตอนที่แล้วซึ่งได้อธิบายถึงการวิเคราะห์การถดถอยเชิงเส้นในมิติเดียว https://phyblas.hinaboshi.com/20161210
คราวนี้จะขยายไปสู่ปัญหาที่เป็นทั่วไปมากขึ้น คือกรณีที่มีมากกว่าหนึ่งมิติ
ในธรรมชาติแล้ว ค่าของอะไรต่างๆมักไม่ได้ขึ้นอยู่กับปัจจัยอะไรเพียงอย่างเดียว มีสิ่งที่มาเกี่ยวข้องด้วยมากมาย
แบบนี้ค่าผลลัพธ์อาจหาได้จากผลรวมของค่าของตัวแปรตามแต่ละตัวคูณด้วยน้ำหนักของตัวแปรต้นนั้น แล้วบวกด้วยค่าไบแอส
โดย n เป็นจำนวนมิติ (จำนวนตัวแปรต้น) ของปัญหา
ในที่นี้ j เป็นเลขลำดับของตัวแปรต้น แต่ละตัวแปรต้นมีค่าน้ำหนักของตัวเอง ซึ่งเป็นตัวบอกว่าตัวแปรต้นนั้นมีความสำคัญ มีอิทธิพลต่อผลลัพธ์แค่ไหน
ค่า SSE ยังคงหาได้จากสมการเดิมเหมือนตอนมิติเดียว เพียงแต่ค่า h มีจำนวนพจน์ที่ต้องบวกกันมากขึ้นเท่านั้น
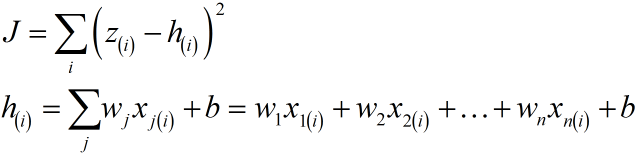
ค่าอนุพันธ์ย่อยสำหรับน้ำหนักแต่ละตัวก็จะเป็นไปตามนี้
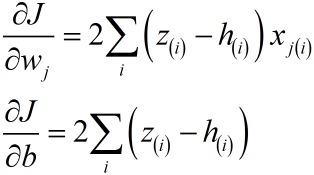
และค่าน้ำหนักที่ต้องเปลี่ยนแปลงในแต่ละครั้งของการเรียนรู้ก็จะเป็น
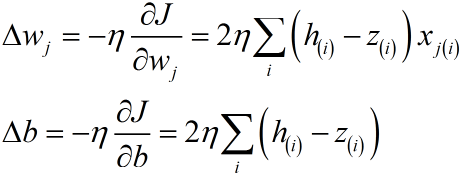
ขอเริ่มจากยกตัวอย่างโจทย์ปัญหาในสองมิติ
สมมุติว่าเล่นเกมเกมหนึ่ง ในนั้นมีให้เลี้ยงอสูรเพื่อไปต่อสู้กัน และพลังโจมตีของอสูรขึ้นกับอาหารที่ทาน
ผู้เล่นคนหนึ่งทดลองเลี้ยงอสูรหลายตัวโดยให้อาหารในปริมาณต่างๆกันแล้วดูว่าสุดท้ายแล้วอสูรมีพลังโจมตีเท่าไหร่
สมมุติว่าอาหารที่ควบคุมให้เป็นตัวแปรต้นนั้นมีอยู่สองชนิดคือผลไม้กับผัก
ผลที่ได้สามารถวาดกราฟออกมาได้ดังนี้
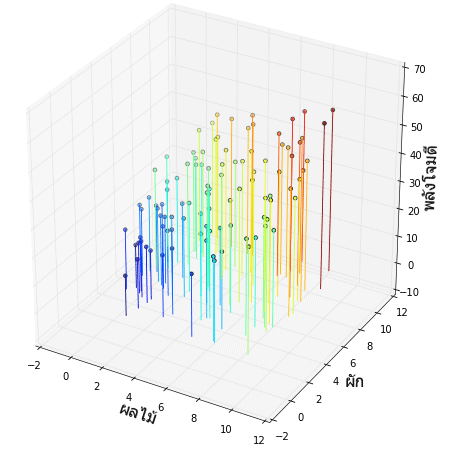
โดยในแกน x และ y คือปริมาณผลไม้และผักที่ให้อสูรทาน แกน z เป็นพลังโจมตี
ในภาพจะเห็นแนวโน้มเป็นเชิงเส้นชัดเจน ยิ่งให้อาหารมากก็ยิ่งพลังโจมตีสูง
เนื่องจากมีสองตัวแปร จึงอาจสมมุติสมการของคำตอบได้เป็น
โค้ดของภาพนี้เป็นดังนี้
จากโค้ดนี้จะเห็นได้ว่าคำตอบคือ w1=2, w2=3, b=10
พจน์ random ที่เพิ่มเข้ามาเป็นความไม่แน่นอนซึ่งเกิดจากปัจจัยต่างๆ เช่นอาหารชนิดอื่นที่เราไม่ได้ควบคุม หรืออาจเกิดจากค่าสุ่มต่างๆในเกมก็ได้
วิธีการแก้ปัญหาเราจะนำโค้ดจากตอนที่แล้วซึ่งใช้วิธีการเคลื่อนลงตามความชันในหนึ่งมิติมาแก้เล็กน้อยให้ใช้สำหรับปัญหาสองมิติได้
เขียนได้ดังนี้
ที่เปลี่ยนไปจากเดิมมีแค่แทนที่จะเป็น dw ตัวเดียวก็ใช้เป็น dw1 และ dw2 เวลาที่คำนวณอะไรต่างๆก็ต้องทำทั้ง ๒ อัน
เท่านี้ค่าน้ำหนัก w1, w2 และ b ก็ควรจะเป็นค่าตามที่ต้องการแล้ว
ลองดูผลลัพธ์ด้วยการวาดระนาบของค่าที่ทำนายจากค่าน้ำหนักและไบแอสที่ได้ในท้ายสุด โดยวาดจุดของค่าคำตอบจริงและลากเส้นค่าส่วนต่างเพื่อเปรียบเทียบให้เห็นความคลาดเคลื่อนด้วย
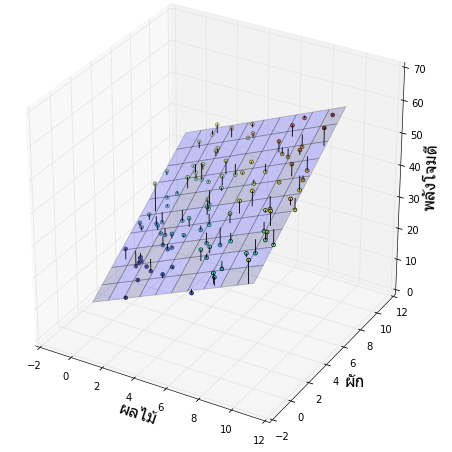
ผลลัพธ์เป็นไปตามที่ควรจะเป็น
แต่ว่าโค้ดนี้จำเพาะสำหรับปัญหาสองมิติ ถ้ามีจำนวนมิติมากกว่านั้นก็ต้องมาคอยแก้โค้ดใหม่เรื่อยๆอาจจะไม่สะดวก เพื่อที่จะให้สามารถใช้แก้ปัญหาในมิติใดๆได้เรายังควรจะปรับปรุงโค้ดอีก
ในกรณีนี้เราจะเปลี่ยนค่าน้ำหนักและไบแอสจากที่เดิมใช้เป็นตัวแปรเป็น w1,w2 และ b เป็นมาเก็บอยู่ในตัวแปรเดียวเป็นอาเรย์คือ w
ส่วนค่าตัวแปรต้นเองก็รวมเป็นอาเรย์สองมิติโดยใช้ np.stack
เขียนออกมาได้ดังนี้
โค้ดนี้จะให้ผลเหมือนกับอันก่อน แต่การเขียนดูสั้นลงเพราะทั้งค่าน้ำหนักและค่าตัวแปรต้นแต่ละตัวอยู่ในอาเรย์เดียวจึงคำนวณไปพร้อมกัน
ต่อจากนั้น เราสามารถทำให้การคำนวณดูเป็นระบบเรียบร้อยมากขึ้นและสามารถนำกลับมาใช้ซ้ำได้ง่ายด้วยการสร้างแบบจำลองการถดถอยเชิงเส้นเป็นคลาสขึ้นมา
ลองเขียนคลาสออกมาได้ตามนี้
การใช้งานจะเริ่มต้นจากสร้างออบเจ็กต์ของคลาสขึ้นมา จากนั้นก็นำข้อมูลที่เตรียมไว้สำหรับเรียนรู้มาทำการเรียนรู้ด้วยเมธอด rianru
พอเรียนรู้เสร็จค่าน้ำหนักที่เก็บอยู่ในแอตทริบิวต์ w ก็จะถูกปรับค่าเรียบร้อย สามารถนำมาใช้คำนวณค่าได้
และเพื่อให้การคำนวณค่าทำได้สะดวกจึงสร้างเมธอด thamnai เอาไว้คำนวณ สามารถดึงมาใช้หาค่าได้ทันที
ตัวอย่างการใช้ ลองเขียนแบบนี้ดูก็จะได้ผลออกมาเหมือนกับตอนแรก
นอกจากนี้ค่า SSE ในแต่ละขั้นยังถูกเก็บไว้ในแอตทริบิวต์ sse ด้วย ลองนำมาวาดกราฟดูได้
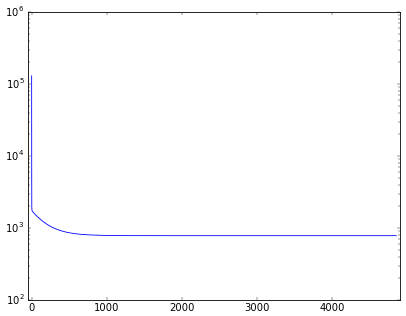
ก็จะเห็นได้ว่า SSE ลดลงเรื่อยๆเมื่อการเรียนรู้เดินหน้าไปจนลู่เข้าค่าหนึ่ง
จะเห็นว่าพอสร้างแบบจำลองเป็นคลาสขึ้นมาแบบนี้แล้วทำให้การใช้ดูสะดวกและเป็นระบบขึ้นมา
สุดท้ายนี้ ลองเปลี่ยนโจทย์ดูบ้าง เพื่อจะทดสอบว่าแบบจำลองที่เขียนขึ้นมานั้นใช้ได้กับกี่มิติก็ได้
สมมุติว่าในเกมเดียวกันนี้เราพบว่าพลังป้องกันของอสูรขึ้นกับค่าอาหารหลายชนิด ได้แก่ ผลไม้ ผัก เนื้อ แป้ง ไขมัน รวมทั้งหมด ๕ อย่าง
เขียนโค้ดสร้างข้อมูลตามนี้
แค่ดูโค้ดก็คงพอรู้คำตอบอยู่แล้วว่า w ของอาหารแต่ละชนิดเป็นเท่าไหร่ อาหารชนิดไหนมีความสำคัญมากกว่า
จากนั้นลองมาดูว่าเราจะใช้คลาสที่สร้างขึ้นนี้เพื่อหาคำตอบได้เป็นไปตามนั้นหรือเปล่า
พอมิติสูงขึ้นการจะวาดภาพให้เห็นก็กลายเป็นเรื่องยาก ดังนั้นครั้งนี้ขอแค่วาดกราฟดูผลว่าค่า SSE ลดลงเรื่อยๆ และแสดงค่า w ว่าเป็นไปตามที่ควรจะเป็นจริงๆ
จะเห็นว่าค่า w ได้ใกล้เคียงกับค่าจริงคือ [1.2,0.5,0.3,0.2,0.7,0.1] โดยมีความคลาดเคลื่อนเล็กน้อยที่เกิดจากค่าสุ่ม
ตอนนี้สามารถสร้างแบบจำลองการถดถอยเชิงเส้นสำหรับหลายมิติได้แล้ว
การถดถอยเชิงเส้นเป็นพื้นฐานสำคัญที่ต่อยอดไปสู่เทคนิคอื่นๆอีกหลายอย่าง เช่นการถดถอยโลจิสติกซึ่งนำค่าที่ได้จากการคำนวณเชิงเส้นมาใช้ในการตัดแยกกลุ่มข้อมูลตามค่า
อ่านเรื่องการวิเคราะห์การถดถอยโลจิสติกได้ใน https://phyblas.hinaboshi.com/20161103
คราวนี้จะขยายไปสู่ปัญหาที่เป็นทั่วไปมากขึ้น คือกรณีที่มีมากกว่าหนึ่งมิติ
ในธรรมชาติแล้ว ค่าของอะไรต่างๆมักไม่ได้ขึ้นอยู่กับปัจจัยอะไรเพียงอย่างเดียว มีสิ่งที่มาเกี่ยวข้องด้วยมากมาย
แบบนี้ค่าผลลัพธ์อาจหาได้จากผลรวมของค่าของตัวแปรตามแต่ละตัวคูณด้วยน้ำหนักของตัวแปรต้นนั้น แล้วบวกด้วยค่าไบแอส
h = x1w1 + x2w2 + ... + xnwn + b
โดย n เป็นจำนวนมิติ (จำนวนตัวแปรต้น) ของปัญหา
ในที่นี้ j เป็นเลขลำดับของตัวแปรต้น แต่ละตัวแปรต้นมีค่าน้ำหนักของตัวเอง ซึ่งเป็นตัวบอกว่าตัวแปรต้นนั้นมีความสำคัญ มีอิทธิพลต่อผลลัพธ์แค่ไหน
ค่า SSE ยังคงหาได้จากสมการเดิมเหมือนตอนมิติเดียว เพียงแต่ค่า h มีจำนวนพจน์ที่ต้องบวกกันมากขึ้นเท่านั้น
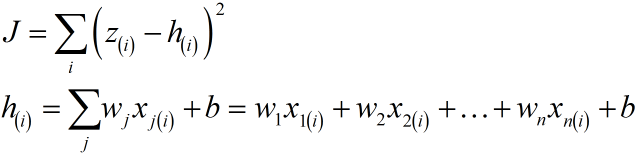
ค่าอนุพันธ์ย่อยสำหรับน้ำหนักแต่ละตัวก็จะเป็นไปตามนี้
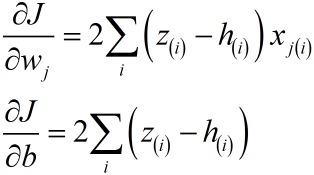
และค่าน้ำหนักที่ต้องเปลี่ยนแปลงในแต่ละครั้งของการเรียนรู้ก็จะเป็น
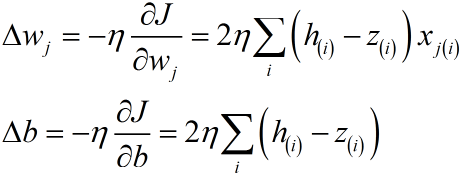
ขอเริ่มจากยกตัวอย่างโจทย์ปัญหาในสองมิติ
สมมุติว่าเล่นเกมเกมหนึ่ง ในนั้นมีให้เลี้ยงอสูรเพื่อไปต่อสู้กัน และพลังโจมตีของอสูรขึ้นกับอาหารที่ทาน
ผู้เล่นคนหนึ่งทดลองเลี้ยงอสูรหลายตัวโดยให้อาหารในปริมาณต่างๆกันแล้วดูว่าสุดท้ายแล้วอสูรมีพลังโจมตีเท่าไหร่
สมมุติว่าอาหารที่ควบคุมให้เป็นตัวแปรต้นนั้นมีอยู่สองชนิดคือผลไม้กับผัก
ผลที่ได้สามารถวาดกราฟออกมาได้ดังนี้

โดยในแกน x และ y คือปริมาณผลไม้และผักที่ให้อสูรทาน แกน z เป็นพลังโจมตี
ในภาพจะเห็นแนวโน้มเป็นเชิงเส้นชัดเจน ยิ่งให้อาหารมากก็ยิ่งพลังโจมตีสูง
เนื่องจากมีสองตัวแปร จึงอาจสมมุติสมการของคำตอบได้เป็น
h = x1w1 + x2w2 + b
โค้ดของภาพนี้เป็นดังนี้
import numpy as np
import matplotlib.pyplot as plt
phonlamai = np.random.uniform(0,10,100) # ปริมาณผลไม้
phak = np.random.uniform(0,10,100) # ปริมาณผัก
chomti = 10+phonlamai*2+phak*3+np.random.randn(100)*3 # คำนวณพลังโจมตี
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d')
ax.set_xlabel(u'ผลไม้',fontname='Tahoma',fontsize=20)
ax.set_ylabel(u'ผัก',fontname='Tahoma',fontsize=20)
ax.set_zlabel(u'พลังโจมตี',fontname='Tahoma',fontsize=20)
# กำหนดสีของเส้นและจุดตามค่า
def si(x):
x = (x-chomti.min())/(chomti.max()-chomti.min())
return plt.get_cmap('jet')(x)
# วาดเส้นลากจากพื้นให้กับทุกจุด
for i in range(100):
ax.plot([phonlamai[i],phonlamai[i]],[phak[i],phak[i]],[0,chomti[i]],color=si(chomti[i]))
# วาดจุด
ax.scatter(phonlamai,phak,chomti,c=si(chomti),edgecolor='k')
plt.show()
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
phonlamai = np.random.uniform(0,10,100) # ปริมาณผลไม้
phak = np.random.uniform(0,10,100) # ปริมาณผัก
chomti = 10+phonlamai*2+phak*3+np.random.randn(100)*3 # คำนวณพลังโจมตี
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d')
ax.set_xlabel(u'ผลไม้',fontname='Tahoma',fontsize=20)
ax.set_ylabel(u'ผัก',fontname='Tahoma',fontsize=20)
ax.set_zlabel(u'พลังโจมตี',fontname='Tahoma',fontsize=20)
# กำหนดสีของเส้นและจุดตามค่า
def si(x):
x = (x-chomti.min())/(chomti.max()-chomti.min())
return plt.get_cmap('jet')(x)
# วาดเส้นลากจากพื้นให้กับทุกจุด
for i in range(100):
ax.plot([phonlamai[i],phonlamai[i]],[phak[i],phak[i]],[0,chomti[i]],color=si(chomti[i]))
# วาดจุด
ax.scatter(phonlamai,phak,chomti,c=si(chomti),edgecolor='k')
plt.show()
จากโค้ดนี้จะเห็นได้ว่าคำตอบคือ w1=2, w2=3, b=10
พจน์ random ที่เพิ่มเข้ามาเป็นความไม่แน่นอนซึ่งเกิดจากปัจจัยต่างๆ เช่นอาหารชนิดอื่นที่เราไม่ได้ควบคุม หรืออาจเกิดจากค่าสุ่มต่างๆในเกมก็ได้
วิธีการแก้ปัญหาเราจะนำโค้ดจากตอนที่แล้วซึ่งใช้วิธีการเคลื่อนลงตามความชันในหนึ่งมิติมาแก้เล็กน้อยให้ใช้สำหรับปัญหาสองมิติได้
เขียนได้ดังนี้
eta = 0.0001
n_thamsam = 10000
d_yut = 1e-7
w1,w2,b = 0,0,0
h = w1*phonlamai+w2*phak+b
for i in range(n_thamsam):
dw1 = (2*(chomti-h)*phonlamai).sum()*eta
dw2 = (2*(chomti-h)*phak).sum()*eta
db = 2*(chomti-h).sum()*eta
w1 += dw1
w2 += dw2
b += db
h = w1*phonlamai+w2*phak+b
if(abs(dw1)and abs(dw2)and abs(db)<d_yut):
break
n_thamsam = 10000
d_yut = 1e-7
w1,w2,b = 0,0,0
h = w1*phonlamai+w2*phak+b
for i in range(n_thamsam):
dw1 = (2*(chomti-h)*phonlamai).sum()*eta
dw2 = (2*(chomti-h)*phak).sum()*eta
db = 2*(chomti-h).sum()*eta
w1 += dw1
w2 += dw2
b += db
h = w1*phonlamai+w2*phak+b
if(abs(dw1)and abs(dw2)and abs(db)<d_yut):
break
ที่เปลี่ยนไปจากเดิมมีแค่แทนที่จะเป็น dw ตัวเดียวก็ใช้เป็น dw1 และ dw2 เวลาที่คำนวณอะไรต่างๆก็ต้องทำทั้ง ๒ อัน
เท่านี้ค่าน้ำหนัก w1, w2 และ b ก็ควรจะเป็นค่าตามที่ต้องการแล้ว
ลองดูผลลัพธ์ด้วยการวาดระนาบของค่าที่ทำนายจากค่าน้ำหนักและไบแอสที่ได้ในท้ายสุด โดยวาดจุดของค่าคำตอบจริงและลากเส้นค่าส่วนต่างเพื่อเปรียบเทียบให้เห็นความคลาดเคลื่อนด้วย
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d')
ax.set_xlabel(u'ผลไม้',fontname='Tahoma',fontsize=20)
ax.set_ylabel(u'ผัก',fontname='Tahoma',fontsize=20)
ax.set_zlabel(u'พลังโจมตี',fontname='Tahoma',fontsize=20)
# สร้างโครงข่ายพื้นผิวค่าทำนาย
mx,my = np.meshgrid(np.linspace(0,10,11),np.linspace(0,10,11))
# คำนวณค่าทำนายบนพื้นผิวจากค่าน้ำหนักที่ได้
mz = b+mx*w1+my*w2
# วาดพื้นผิว
ax.plot_surface(mx,my,mz,rstride=1,cstride=1,alpha=0.2,color='b',edgecolor='k')
h = phonlamai*w1+phak*w2+b
# วาดเส้นเชื่อมระหว่างจุดของค่าจริงกับระนาบที่ทำนาย
for i in range(100):
ax.plot([phonlamai[i],phonlamai[i]],[phak[i],phak[i]],[h[i],chomti[i]],'k')
# จุดของค่าจริง
ax.scatter(phonlamai,phak,chomti,c=chomti,edgecolor='k',cmap='jet')
plt.show()
print(b,w1,w2)
# (9.964693266998049, 2.1468002594406337, 2.8872801897811629)
ax = plt.axes([0,0,1,1],projection='3d')
ax.set_xlabel(u'ผลไม้',fontname='Tahoma',fontsize=20)
ax.set_ylabel(u'ผัก',fontname='Tahoma',fontsize=20)
ax.set_zlabel(u'พลังโจมตี',fontname='Tahoma',fontsize=20)
# สร้างโครงข่ายพื้นผิวค่าทำนาย
mx,my = np.meshgrid(np.linspace(0,10,11),np.linspace(0,10,11))
# คำนวณค่าทำนายบนพื้นผิวจากค่าน้ำหนักที่ได้
mz = b+mx*w1+my*w2
# วาดพื้นผิว
ax.plot_surface(mx,my,mz,rstride=1,cstride=1,alpha=0.2,color='b',edgecolor='k')
h = phonlamai*w1+phak*w2+b
# วาดเส้นเชื่อมระหว่างจุดของค่าจริงกับระนาบที่ทำนาย
for i in range(100):
ax.plot([phonlamai[i],phonlamai[i]],[phak[i],phak[i]],[h[i],chomti[i]],'k')
# จุดของค่าจริง
ax.scatter(phonlamai,phak,chomti,c=chomti,edgecolor='k',cmap='jet')
plt.show()
print(b,w1,w2)
# (9.964693266998049, 2.1468002594406337, 2.8872801897811629)

ผลลัพธ์เป็นไปตามที่ควรจะเป็น
แต่ว่าโค้ดนี้จำเพาะสำหรับปัญหาสองมิติ ถ้ามีจำนวนมิติมากกว่านั้นก็ต้องมาคอยแก้โค้ดใหม่เรื่อยๆอาจจะไม่สะดวก เพื่อที่จะให้สามารถใช้แก้ปัญหาในมิติใดๆได้เรายังควรจะปรับปรุงโค้ดอีก
ในกรณีนี้เราจะเปลี่ยนค่าน้ำหนักและไบแอสจากที่เดิมใช้เป็นตัวแปรเป็น w1,w2 และ b เป็นมาเก็บอยู่ในตัวแปรเดียวเป็นอาเรย์คือ w
ส่วนค่าตัวแปรต้นเองก็รวมเป็นอาเรย์สองมิติโดยใช้ np.stack
เขียนออกมาได้ดังนี้
eta = 0.0001
n_sungsut = 10000
d_yut = 1e-7
ahan = np.stack([phonlamai,phak],1)
w = np.zeros(ahan.shape[1]+1)
dw = np.zeros(ahan.shape[1]+1)
h = np.dot(ahan,w[1:])+w[0]
for i in range(n_sungsut):
dw[1:] = 2*np.dot(chomti-h,ahan)*eta
dw[0] = 2*(chomti-h).sum()*eta
w += dw
h = np.dot(ahan,w[1:])+w[0]
if(np.all(abs(dw)<d_yut)):
break # หยุดเฉพาะเมื่อค่าน้ำหนักทุกตัวเปลี่ยนแปลงน้อยกว่า d_yut
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d')
ax.set_xlabel(u'ผลไม้',fontname='Tahoma',fontsize=20)
ax.set_ylabel(u'ผัก',fontname='Tahoma',fontsize=20)
ax.set_zlabel(u'พลังโจมตี',fontname='Tahoma',fontsize=20)
mx,my = np.meshgrid(np.linspace(0,10,11),np.linspace(0,10,11))
mz = w[0]+mx*w[1]+my*w[2]
ax.plot_surface(mx,my,mz,rstride=1,cstride=1,alpha=0.2)
h = phonlamai*w[1]+phak*w[2]+w[0]
for i in range(100):
ax.plot([phonlamai[i],phonlamai[i]],[phak[i],phak[i]],[h[i],chomti[i]],'k')
ax.scatter(phonlamai,phak,chomti,c=chomti,edgecolor='k',cmap='jet')
plt.show()
print(w)
n_sungsut = 10000
d_yut = 1e-7
ahan = np.stack([phonlamai,phak],1)
w = np.zeros(ahan.shape[1]+1)
dw = np.zeros(ahan.shape[1]+1)
h = np.dot(ahan,w[1:])+w[0]
for i in range(n_sungsut):
dw[1:] = 2*np.dot(chomti-h,ahan)*eta
dw[0] = 2*(chomti-h).sum()*eta
w += dw
h = np.dot(ahan,w[1:])+w[0]
if(np.all(abs(dw)<d_yut)):
break # หยุดเฉพาะเมื่อค่าน้ำหนักทุกตัวเปลี่ยนแปลงน้อยกว่า d_yut
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d')
ax.set_xlabel(u'ผลไม้',fontname='Tahoma',fontsize=20)
ax.set_ylabel(u'ผัก',fontname='Tahoma',fontsize=20)
ax.set_zlabel(u'พลังโจมตี',fontname='Tahoma',fontsize=20)
mx,my = np.meshgrid(np.linspace(0,10,11),np.linspace(0,10,11))
mz = w[0]+mx*w[1]+my*w[2]
ax.plot_surface(mx,my,mz,rstride=1,cstride=1,alpha=0.2)
h = phonlamai*w[1]+phak*w[2]+w[0]
for i in range(100):
ax.plot([phonlamai[i],phonlamai[i]],[phak[i],phak[i]],[h[i],chomti[i]],'k')
ax.scatter(phonlamai,phak,chomti,c=chomti,edgecolor='k',cmap='jet')
plt.show()
print(w)
โค้ดนี้จะให้ผลเหมือนกับอันก่อน แต่การเขียนดูสั้นลงเพราะทั้งค่าน้ำหนักและค่าตัวแปรต้นแต่ละตัวอยู่ในอาเรย์เดียวจึงคำนวณไปพร้อมกัน
ต่อจากนั้น เราสามารถทำให้การคำนวณดูเป็นระบบเรียบร้อยมากขึ้นและสามารถนำกลับมาใช้ซ้ำได้ง่ายด้วยการสร้างแบบจำลองการถดถอยเชิงเส้นเป็นคลาสขึ้นมา
ลองเขียนคลาสออกมาได้ตามนี้
class ThotthoiChoengsen:
def __init__(self,eta):
self.eta = eta
# เรียนรู้จากข้อมูล X และ z ที่ใส่เข้าไป
def rianru(self,X,z,d_yut=1e-7,n_thamsam=100000):
self.w = np.zeros(X.shape[1]+1)
dw = np.zeros(X.shape[1]+1)
h = self.thamnai(X)
self.sse = [self.ha_sse(h,z)] # ลิสต์บันทึกค่า SSE ในแต่ละรอบ
for i in range(n_thamsam):
eee = 2*(z-h)*self.eta
dw[1:] = np.dot(eee,X)
dw[0] = eee.sum()
self.w += dw
h = self.thamnai(X)
self.sse += [self.ha_sse(h,z)]
if(np.all(abs(dw)<d_yut)):
break
# ทำนายค่าจาก X ที่ใส่เข้าไป
def thamnai(self,X):
return np.dot(X,self.w[1:])+self.w[0]
# หาค่าผลรวมความคลาดเคลื่อนกำลังสอง
def ha_sse(self,h,z):
return ((h-z)**2).sum()
def __init__(self,eta):
self.eta = eta
# เรียนรู้จากข้อมูล X และ z ที่ใส่เข้าไป
def rianru(self,X,z,d_yut=1e-7,n_thamsam=100000):
self.w = np.zeros(X.shape[1]+1)
dw = np.zeros(X.shape[1]+1)
h = self.thamnai(X)
self.sse = [self.ha_sse(h,z)] # ลิสต์บันทึกค่า SSE ในแต่ละรอบ
for i in range(n_thamsam):
eee = 2*(z-h)*self.eta
dw[1:] = np.dot(eee,X)
dw[0] = eee.sum()
self.w += dw
h = self.thamnai(X)
self.sse += [self.ha_sse(h,z)]
if(np.all(abs(dw)<d_yut)):
break
# ทำนายค่าจาก X ที่ใส่เข้าไป
def thamnai(self,X):
return np.dot(X,self.w[1:])+self.w[0]
# หาค่าผลรวมความคลาดเคลื่อนกำลังสอง
def ha_sse(self,h,z):
return ((h-z)**2).sum()
การใช้งานจะเริ่มต้นจากสร้างออบเจ็กต์ของคลาสขึ้นมา จากนั้นก็นำข้อมูลที่เตรียมไว้สำหรับเรียนรู้มาทำการเรียนรู้ด้วยเมธอด rianru
พอเรียนรู้เสร็จค่าน้ำหนักที่เก็บอยู่ในแอตทริบิวต์ w ก็จะถูกปรับค่าเรียบร้อย สามารถนำมาใช้คำนวณค่าได้
และเพื่อให้การคำนวณค่าทำได้สะดวกจึงสร้างเมธอด thamnai เอาไว้คำนวณ สามารถดึงมาใช้หาค่าได้ทันที
ตัวอย่างการใช้ ลองเขียนแบบนี้ดูก็จะได้ผลออกมาเหมือนกับตอนแรก
eta = 0.0001
ahan = np.stack([phonlamai,phak],1)
tc = ThotthoiChoengsen(eta) # สร้างออบเจ็กต์
tc.rianru(ahan,chomti) # เริ่มการเรียนรู้
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d')
ax.set_xlabel(u'ผลไม้',fontname='Tahoma',fontsize=20)
ax.set_ylabel(u'ผัก',fontname='Tahoma',fontsize=20)
ax.set_zlabel(u'พลังโจมตี',fontname='Tahoma',fontsize=20)
mx,my = np.meshgrid(np.linspace(0,10,11),np.linspace(0,10,11))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = tc.thamnai(mX).reshape(11,11)
ax.plot_surface(mx,my,mz,rstride=1,cstride=1,alpha=0.2)
h = tc.thamnai(ahan)
for i in range(100):
ax.plot([phonlamai[i],phonlamai[i]],[phak[i],phak[i]],[h[i],chomti[i]],'k')
ax.scatter(phonlamai,phak,chomti,c=chomti)
plt.show()
print(tc.w)
ahan = np.stack([phonlamai,phak],1)
tc = ThotthoiChoengsen(eta) # สร้างออบเจ็กต์
tc.rianru(ahan,chomti) # เริ่มการเรียนรู้
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d')
ax.set_xlabel(u'ผลไม้',fontname='Tahoma',fontsize=20)
ax.set_ylabel(u'ผัก',fontname='Tahoma',fontsize=20)
ax.set_zlabel(u'พลังโจมตี',fontname='Tahoma',fontsize=20)
mx,my = np.meshgrid(np.linspace(0,10,11),np.linspace(0,10,11))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = tc.thamnai(mX).reshape(11,11)
ax.plot_surface(mx,my,mz,rstride=1,cstride=1,alpha=0.2)
h = tc.thamnai(ahan)
for i in range(100):
ax.plot([phonlamai[i],phonlamai[i]],[phak[i],phak[i]],[h[i],chomti[i]],'k')
ax.scatter(phonlamai,phak,chomti,c=chomti)
plt.show()
print(tc.w)
นอกจากนี้ค่า SSE ในแต่ละขั้นยังถูกเก็บไว้ในแอตทริบิวต์ sse ด้วย ลองนำมาวาดกราฟดูได้
plt.figure()
plt.axes(yscale='log',xlim=[-len(tc.sse)*0.01,len(tc.sse)*1.01])
plt.plot(tc.sse)
plt.show()
plt.axes(yscale='log',xlim=[-len(tc.sse)*0.01,len(tc.sse)*1.01])
plt.plot(tc.sse)
plt.show()

ก็จะเห็นได้ว่า SSE ลดลงเรื่อยๆเมื่อการเรียนรู้เดินหน้าไปจนลู่เข้าค่าหนึ่ง
จะเห็นว่าพอสร้างแบบจำลองเป็นคลาสขึ้นมาแบบนี้แล้วทำให้การใช้ดูสะดวกและเป็นระบบขึ้นมา
สุดท้ายนี้ ลองเปลี่ยนโจทย์ดูบ้าง เพื่อจะทดสอบว่าแบบจำลองที่เขียนขึ้นมานั้นใช้ได้กับกี่มิติก็ได้
สมมุติว่าในเกมเดียวกันนี้เราพบว่าพลังป้องกันของอสูรขึ้นกับค่าอาหารหลายชนิด ได้แก่ ผลไม้ ผัก เนื้อ แป้ง ไขมัน รวมทั้งหมด ๕ อย่าง
เขียนโค้ดสร้างข้อมูลตามนี้
# สร้างอาเรย์ ๕ หลักเท่ากับจำนวนชนิดของอาหาร
ahan = np.random.uniform(0,10,[100,5])
# คำนวณพลังป้องกันจากอาหารทั้ง ๕ ชนิด พร้อมใส่ค่าสุ่มไปด้วย
pongkan = 1.2+ahan[:,0]*0.5+ahan[:,1]*0.3+ahan[:,2]*0.2+ahan[:,3]*0.7+ahan[:,4]*0.1+np.random.randn(100)*0.1
ahan = np.random.uniform(0,10,[100,5])
# คำนวณพลังป้องกันจากอาหารทั้ง ๕ ชนิด พร้อมใส่ค่าสุ่มไปด้วย
pongkan = 1.2+ahan[:,0]*0.5+ahan[:,1]*0.3+ahan[:,2]*0.2+ahan[:,3]*0.7+ahan[:,4]*0.1+np.random.randn(100)*0.1
แค่ดูโค้ดก็คงพอรู้คำตอบอยู่แล้วว่า w ของอาหารแต่ละชนิดเป็นเท่าไหร่ อาหารชนิดไหนมีความสำคัญมากกว่า
จากนั้นลองมาดูว่าเราจะใช้คลาสที่สร้างขึ้นนี้เพื่อหาคำตอบได้เป็นไปตามนั้นหรือเปล่า
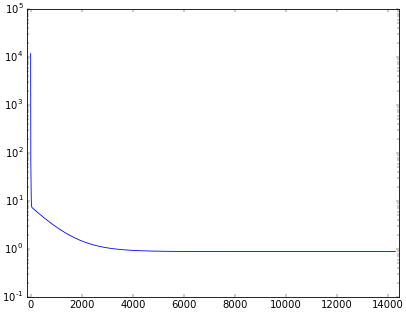
พอมิติสูงขึ้นการจะวาดภาพให้เห็นก็กลายเป็นเรื่องยาก ดังนั้นครั้งนี้ขอแค่วาดกราฟดูผลว่าค่า SSE ลดลงเรื่อยๆ และแสดงค่า w ว่าเป็นไปตามที่ควรจะเป็นจริงๆ
eta = 0.00005
tc = ThotthoiChoengsen(eta)
tc.rianru(ahan,pongkan)
plt.figure()
plt.axes(yscale='log',xlim=[-len(tc.sse)*0.01,len(tc.sse)*1.01])
plt.plot(tc.sse)
plt.show()
print(tc.w)
# [ 1.12368741 0.49667723 0.29609156 0.20440074 0.70637367 0.10687599]
tc = ThotthoiChoengsen(eta)
tc.rianru(ahan,pongkan)
plt.figure()
plt.axes(yscale='log',xlim=[-len(tc.sse)*0.01,len(tc.sse)*1.01])
plt.plot(tc.sse)
plt.show()
print(tc.w)
# [ 1.12368741 0.49667723 0.29609156 0.20440074 0.70637367 0.10687599]

จะเห็นว่าค่า w ได้ใกล้เคียงกับค่าจริงคือ [1.2,0.5,0.3,0.2,0.7,0.1] โดยมีความคลาดเคลื่อนเล็กน้อยที่เกิดจากค่าสุ่ม
ตอนนี้สามารถสร้างแบบจำลองการถดถอยเชิงเส้นสำหรับหลายมิติได้แล้ว
การถดถอยเชิงเส้นเป็นพื้นฐานสำคัญที่ต่อยอดไปสู่เทคนิคอื่นๆอีกหลายอย่าง เช่นการถดถอยโลจิสติกซึ่งนำค่าที่ได้จากการคำนวณเชิงเส้นมาใช้ในการตัดแยกกลุ่มข้อมูลตามค่า
อ่านเรื่องการวิเคราะห์การถดถอยโลจิสติกได้ใน https://phyblas.hinaboshi.com/20161103
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib