วิธีการเพื่อนบ้านใกล้สุด k ตัวโดยใช้ sklearn
เขียนเมื่อ 2017/10/31 18:27
แก้ไขล่าสุด 2022/07/21 14:59
หลังจากที่ได้แนะนำการเขียนคลาสของวิธีการเพื่อนบ้านใกล้สุด k ตัวด้วยตัวเองไปแล้ว https://phyblas.hinaboshi.com/20171028
แต่ว่าคลาสที่เขียนนั้นเป็นแค่ของที่ลองสร้างขึ้นเองเพื่อให้เข้าใจหลักการทำงานคร่าวๆเท่านั้น ประสิทธิภาพการใช้งานจริงๆไม่ค่อยดี ดังนั้นในการใช้งานจริงเราจะใช้ของที่มีคนทำมาไว้เป็นอย่างดีแล้วอย่าง sklearn ดีกว่า
การทำงานของวิธีการเพื่อนบ้านใกล้สุด k ตัวใน sklearn นั้นมีการใช้อัลกอริธึมที่เรียกว่า KD tree หรือ Ball tree ในการค้นหาจุดที่ใกล้ที่สุด แทนที่จะมาคำนวณระยะห่างจากทุกจุด ดังนั้นจึงเร็วกว่า เหมาะแก่การใช้งานจริงๆ
รายละเอียดตรงนั้นค่อนข้างซับซ้อนจึงจะไม่กล่าวถึง ในบทความนี้จะพูดถึงแค่การใช้วิธีการเพื่อนบ้านใกล้สุด k ตัวโดยใช้คลาสใน sklearn
ขอเริ่มจากยกตัวอย่างการใช้ให้ดูแล้วค่อยอธิบายโค้ดทีหลัง
สมมุติว่าต้องการจำแนกแบ่งเขตข้อมูลสองมิติที่มีการกระจายตัวแบบนี้
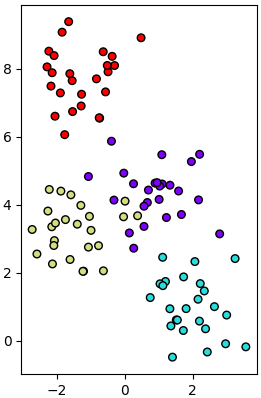
ซึ่งสร้างจากโค้ดนี้
เมื่อลองทำการแบ่งเขตด้วยวิธีการเพื่อนบ้านใกล้สุด k ตัวก็ทำได้ดังนี้
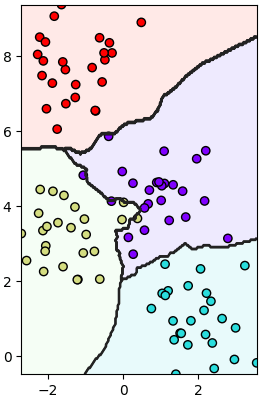
วิธีการใช้อาจเอาไปเทียบกับการถดถอยโลจิสติกที่ได้เขียนถึงไปใน https://phyblas.hinaboshi.com/20171010
นั่นคือสามารถสรุปง่ายๆว่าขั้นตอนการใช้งานหลักๆก็คือ
1. สร้างออบเจ็กต์จากคลาส KNeighborsClassifier (ในที่นี้ย่อเป็น Knn)
2. นำออบเจ็กต์ที่ได้มาใช้เมธอด fit เพื่อทำการเรียนรู้ข้อมูลที่ป้อนเข้าไป
3. ทำนายหมวดหมู่ของจุดที่ต้องการโดยใช้เมธอด predict
ตัวอย่างข้างต้นใช้ไปโดยที่ใช้ค่าต่างๆเป็นค่าตั้งต้นทั้งหมดไม่ได้ปรับแต่งอะไร แต่ว่าเราสามารถปรับแต่งอะไรได้หลายอย่าง อาร์กิวเมนต์มีดังนี้
n_neighbors
คือจำนวนเพื่อนบ้านที่จะพิจารณา
ค่าตั้งต้นคือ 5
weights
วิธีการคิดน้ำหนัก กรณีที่จำนวนเพื่อนบ้านมากกว่า 1 โดยเลือกได้ ๒ แบบคือ
- uniform คือ คิดน้ำหนักแต่ละจุดเท่ากันไม่ว่าจะระยะห่างเท่าไหร่
- distance คิดน้ำหนักตามส่วนกลับของระยะทางของจุด ยิ่งใกล้ยิ่งมีน้ำหนักมาก
นอกจากนี้ยังอาจใส่เป็นฟังก์ชันบางอย่างสำหรับคิด โดยฟังก์ชันจะต้องรับอาเรย์ของค่าระยะทางไปคำนวณแล้วคืนค่ากลับมาเป็นอาเรย์รูปร่างเดิม
ค่าตั้งต้นคือ uniform
algorithm
วิธีการคิดเพื่อค้นหาจุดที่ใกล้ที่สุด ใส่ได้ ๔ อย่างคือ
- ball_tree คือ ใช้วิธี Ball tree
- kd_tree คือ ใช้วิธี KD tree
- brute คือ คำนวณทั้งหมด
- auto เลือกวิธีการเองตามความเหมาะสม ขึ้นกับข้อมูลที่ใส่เข้าไป
ค่าตั้งต้นคือ auto
metric
มาตรวัดระยะทาง (วิธีการคิดว่าจะคำนวณระยะทางยังไง)
มีอยู่หลายวิธี แต่ในกรณีส่วนใหญ่จะใช้ minkowski คือ sum(|x - y|^p)^(1/p)
ค่าตั้งต้นคือ minkowski
มาตรวัดแบบอื่นดูได้ที่ http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.DistanceMetric.html
p
จำนวนเลขชี้กำลัง สำหรับ minkowski
ค่าตั้งต้นคือ 2
n_jobs
จำนวนจ็อบในการรันแบบคู่ขนานในกรณีที่คอมมีหลายคอร์ ถ้าใส่ -1 จะใช้คอร์ทั้งหมดเท่าที่มี
ค่าตั้งต้นคือ 1
ตัวอย่าง ลองปรับบางค่า เช่นลองแก้บรรทัดที่สร้าง knn เป็น
ผลที่ได้ก็จะเปลี่ยนไป กลายเป็นแบบนี้
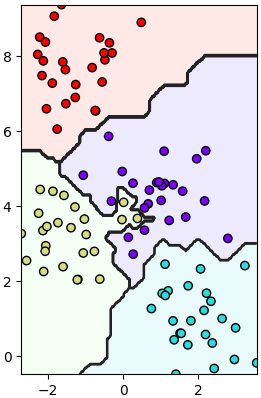
สังเกตได้ว่าเส้นแบ่งเป็นเส้นตรง เพราะระยะทางถูกคำนวณจากผลรวมค่าสัมบูรณ์ แทนที่จะเป็นยกกำลังสอง
ต่อมาลองเปรียบเทียบอัลกอริธึมดูบ้าง ลองเขียนแบบนี้ ข้อมูลมี 1000 ตัว แล้วตัวแปรต้นมี 10 ชนิด
ได้
จะเห็นได้ว่าการใช้ ball_tree หรือ kd_tree นั้นได้ผลเร็วกว่า brute ซึ่งเป็นการคำนวณทั้งหมดมาก ส่วน auto ในที่นี้ kd_tree ถูกเลือก จึงได้ผลเท่ากัน
ต่อมาลองทดสอบเรื่องจำนวนจ็อบดูด้วย
ได้
ยิ่งจ็อบเยอะก็ยิ่งเร็ว แต่เครื่องก็ทำงานหนักเต็มที่ขึ้นตาม
นอกจากนี้ในตัวออบเจ็กต์ knn ยังมีเมธอดน่าสนในอื่นๆที่สามารถใช้ได้ ได้แก่
.kneighbors
จะคืนค่าระยะห่างของเพื่อนบ้านที่ถูกใช้ พร้อมกับดัชนีของจุดนั้น
ตัวอย่าง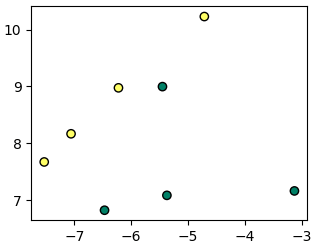
สามารถใส่คีย์เวิร์ดเพิ่มเติมได้แก่
- n_neighbors จำนวนเพื่อนบ้านที่จะให้คืนค่ากลับมา หากไม่ใส่จะคืนเท่ากับค่า n_neighbors ที่กำหนดให้ตั้งแต่ตอนแรก
- return_distance ถ้าใส่เป็น 0 จะไม่คืนค่าระยะทางกลับมา แต่จะคืนแค่อย่างเดียวคือดัชนีของจุด
ลองใส่ดู
.kneighbors_graph
จะคืนค่าที่แสดงว่าตัวไหนเป็นเพื่อนบ้านของตัวนั้นบ้าง
เพียงแต่ว่าผลที่ได้จะอยู่ในรูปของ sparse matrix ดังนั้นเพื่อให้เห็นชัดสามารถแปลงเป็นอาเรย์ธรรมดาได้โดยเมธอด .toarray อีกที
ได้
ถ้าใส่คีย์เวิร์ด mode='distance' ลงไปจะคืนค่าเป็นระยะทางแทน แล้วก็มีคีย์เวิร์ด n_neighbors สามารถเปลี่ยนจำนวนเพื่อนบ้านที่พิจารณาได้ด้วย
ตัวอย่าง
ได้
.predict_proba
เป็นการคำนวณความน่าจะเป็นว่าจะอยู่กลุ่มไหน แทนที่จะทำนายชัดลงไปเลยว่าอยู่กลุ่มไหน
ค่าความน่าจะเป็นในที่นี่คล้ายกับในการถดถอยโลจิสติก แต่ต่างกันตรงที่วิธีการคำนวณ
ตัวอย่างเทียบระหว่าง predict กับ predict_proba โดยจะเทียบให้เห็นด้วยว่าค่าจำนวนเพื่อนบ้านต่างกันก็มีความละเอียดในการแบ่งเขตทำนายที่ต่างกัน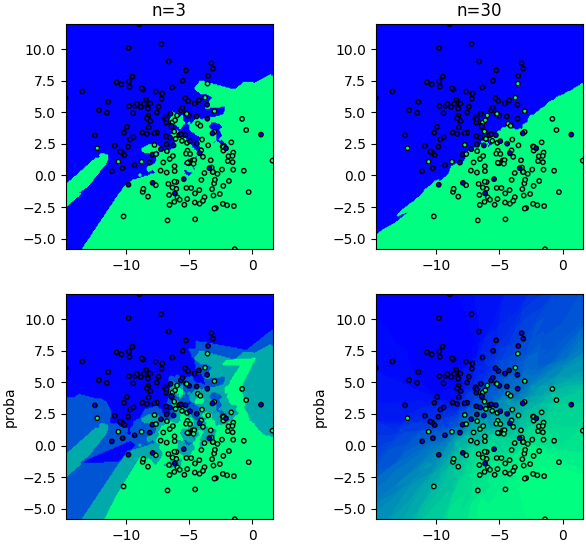
โดยรวมแล้วถือว่า sklearn สามารถใช้งานได้อย่างสะดวกดีมาก
อ้างอิง
แต่ว่าคลาสที่เขียนนั้นเป็นแค่ของที่ลองสร้างขึ้นเองเพื่อให้เข้าใจหลักการทำงานคร่าวๆเท่านั้น ประสิทธิภาพการใช้งานจริงๆไม่ค่อยดี ดังนั้นในการใช้งานจริงเราจะใช้ของที่มีคนทำมาไว้เป็นอย่างดีแล้วอย่าง sklearn ดีกว่า
การทำงานของวิธีการเพื่อนบ้านใกล้สุด k ตัวใน sklearn นั้นมีการใช้อัลกอริธึมที่เรียกว่า KD tree หรือ Ball tree ในการค้นหาจุดที่ใกล้ที่สุด แทนที่จะมาคำนวณระยะห่างจากทุกจุด ดังนั้นจึงเร็วกว่า เหมาะแก่การใช้งานจริงๆ
รายละเอียดตรงนั้นค่อนข้างซับซ้อนจึงจะไม่กล่าวถึง ในบทความนี้จะพูดถึงแค่การใช้วิธีการเพื่อนบ้านใกล้สุด k ตัวโดยใช้คลาสใน sklearn
ขอเริ่มจากยกตัวอย่างการใช้ให้ดูแล้วค่อยอธิบายโค้ดทีหลัง
สมมุติว่าต้องการจำแนกแบ่งเขตข้อมูลสองมิติที่มีการกระจายตัวแบบนี้

ซึ่งสร้างจากโค้ดนี้
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X,z = datasets.make_blobs(n_samples=100,centers=4,cluster_std=0.8,random_state=0)
plt.axes(aspect=1).scatter(X[:,0],X[:,1],c=z,s=30,edgecolor='k',cmap='rainbow')
plt.show()เมื่อลองทำการแบ่งเขตด้วยวิธีการเพื่อนบ้านใกล้สุด k ตัวก็ทำได้ดังนี้
from sklearn.neighbors import KNeighborsClassifier as Knn
knn = Knn()
knn.fit(X,z)
nmesh = 200
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),nmesh),np.linspace(X[:,1].min(),X[:,1].max(),nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = knn.predict(mX).reshape(nmesh,nmesh)
plt.axes(xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()],aspect=1)
plt.contourf(mx,my,mz,alpha=0.1,cmap='rainbow')
plt.contour(mx,my,mz,colors='#222222')
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='rainbow')
plt.show()
วิธีการใช้อาจเอาไปเทียบกับการถดถอยโลจิสติกที่ได้เขียนถึงไปใน https://phyblas.hinaboshi.com/20171010
นั่นคือสามารถสรุปง่ายๆว่าขั้นตอนการใช้งานหลักๆก็คือ
1. สร้างออบเจ็กต์จากคลาส KNeighborsClassifier (ในที่นี้ย่อเป็น Knn)
2. นำออบเจ็กต์ที่ได้มาใช้เมธอด fit เพื่อทำการเรียนรู้ข้อมูลที่ป้อนเข้าไป
3. ทำนายหมวดหมู่ของจุดที่ต้องการโดยใช้เมธอด predict
ตัวอย่างข้างต้นใช้ไปโดยที่ใช้ค่าต่างๆเป็นค่าตั้งต้นทั้งหมดไม่ได้ปรับแต่งอะไร แต่ว่าเราสามารถปรับแต่งอะไรได้หลายอย่าง อาร์กิวเมนต์มีดังนี้
n_neighbors
คือจำนวนเพื่อนบ้านที่จะพิจารณา
ค่าตั้งต้นคือ 5
weights
วิธีการคิดน้ำหนัก กรณีที่จำนวนเพื่อนบ้านมากกว่า 1 โดยเลือกได้ ๒ แบบคือ
- uniform คือ คิดน้ำหนักแต่ละจุดเท่ากันไม่ว่าจะระยะห่างเท่าไหร่
- distance คิดน้ำหนักตามส่วนกลับของระยะทางของจุด ยิ่งใกล้ยิ่งมีน้ำหนักมาก
นอกจากนี้ยังอาจใส่เป็นฟังก์ชันบางอย่างสำหรับคิด โดยฟังก์ชันจะต้องรับอาเรย์ของค่าระยะทางไปคำนวณแล้วคืนค่ากลับมาเป็นอาเรย์รูปร่างเดิม
ค่าตั้งต้นคือ uniform
algorithm
วิธีการคิดเพื่อค้นหาจุดที่ใกล้ที่สุด ใส่ได้ ๔ อย่างคือ
- ball_tree คือ ใช้วิธี Ball tree
- kd_tree คือ ใช้วิธี KD tree
- brute คือ คำนวณทั้งหมด
- auto เลือกวิธีการเองตามความเหมาะสม ขึ้นกับข้อมูลที่ใส่เข้าไป
ค่าตั้งต้นคือ auto
metric
มาตรวัดระยะทาง (วิธีการคิดว่าจะคำนวณระยะทางยังไง)
มีอยู่หลายวิธี แต่ในกรณีส่วนใหญ่จะใช้ minkowski คือ sum(|x - y|^p)^(1/p)
ค่าตั้งต้นคือ minkowski
มาตรวัดแบบอื่นดูได้ที่ http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.DistanceMetric.html
p
จำนวนเลขชี้กำลัง สำหรับ minkowski
ค่าตั้งต้นคือ 2
n_jobs
จำนวนจ็อบในการรันแบบคู่ขนานในกรณีที่คอมมีหลายคอร์ ถ้าใส่ -1 จะใช้คอร์ทั้งหมดเท่าที่มี
ค่าตั้งต้นคือ 1
ตัวอย่าง ลองปรับบางค่า เช่นลองแก้บรรทัดที่สร้าง knn เป็น
knn = Knn(n_neighbors=1,p=1)
# หรือ knn = Knn(1,p=1) ก็ได้ เพราะ n_neighbors เป็นคีย์เวิร์ดลำดับแรกอยู่แล้วผลที่ได้ก็จะเปลี่ยนไป กลายเป็นแบบนี้

สังเกตได้ว่าเส้นแบ่งเป็นเส้นตรง เพราะระยะทางถูกคำนวณจากผลรวมค่าสัมบูรณ์ แทนที่จะเป็นยกกำลังสอง
ต่อมาลองเปรียบเทียบอัลกอริธึมดูบ้าง ลองเขียนแบบนี้ ข้อมูลมี 1000 ตัว แล้วตัวแปรต้นมี 10 ชนิด
import time
X,z = datasets.make_blobs(n_samples=10000,n_features=10,centers=4,random_state=0)
for al in ['ball_tree','kd_tree','brute','auto']:
t1 = time.time()
knn = Knn(algorithm=al)
knn.fit(X,z)
knn.predict(X)
print(u'%s: %.3f วินาที'%(al,time.time()-t1))ได้
ball_tree: 0.670 วินาที
kd_tree: 0.585 วินาที
brute: 3.151 วินาที
auto: 0.585 วินาทีจะเห็นได้ว่าการใช้ ball_tree หรือ kd_tree นั้นได้ผลเร็วกว่า brute ซึ่งเป็นการคำนวณทั้งหมดมาก ส่วน auto ในที่นี้ kd_tree ถูกเลือก จึงได้ผลเท่ากัน
ต่อมาลองทดสอบเรื่องจำนวนจ็อบดูด้วย
X,z = datasets.make_blobs(n_samples=20000,n_features=20,random_state=0)
for j in [1,2,3]:
t1 = time.time()
Knn(n_jobs=j).fit(X,z).predict(X)
print(u'n_jobs=%s: %.3f วินาที'%(j,time.time()-t1))ได้
n_jobs=1: 8.393 วินาที
n_jobs=2: 4.825 วินาที
n_jobs=3: 4.235 วินาทียิ่งจ็อบเยอะก็ยิ่งเร็ว แต่เครื่องก็ทำงานหนักเต็มที่ขึ้นตาม
นอกจากนี้ในตัวออบเจ็กต์ knn ยังมีเมธอดน่าสนในอื่นๆที่สามารถใช้ได้ ได้แก่
.kneighbors
จะคืนค่าระยะห่างของเพื่อนบ้านที่ถูกใช้ พร้อมกับดัชนีของจุดนั้น
ตัวอย่าง
X,z = datasets.make_blobs(n_samples=8,centers=2,random_state=5)
knn = Knn(n_neighbors=3)
knn.fit(X,z)
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='summer')
plt.show()
k = knn.kneighbors(X)
print(k[0])
print(k[1])
for i in range(8):
print(', '.join(['%d > %.2f'%(k[1][i][j],k[0][i][j]) for j in range(3)]))[[ 0. 1.12763922 1.91394086]
[ 0. 0.68420112 1.16141094]
[ 0. 1.43561929 1.9628876 ]
[ 0. 0.77421595 1.16141094]
[ 0. 2.24451596 2.95862282]
[ 0. 1.12763922 1.35891489]
[ 0. 0.77421595 1.43561929]
[ 0. 0.68420112 1.35891489]]
[[0 5 6]
[1 7 3]
[2 6 3]
[3 6 1]
[4 0 6]
[5 0 7]
[6 3 2]
[7 1 5]]
0 > 0.00, 5 > 1.13, 6 > 1.91
1 > 0.00, 7 > 0.68, 3 > 1.16
2 > 0.00, 6 > 1.44, 3 > 1.96
3 > 0.00, 6 > 0.77, 1 > 1.16
4 > 0.00, 0 > 2.24, 6 > 2.96
5 > 0.00, 0 > 1.13, 7 > 1.36
6 > 0.00, 3 > 0.77, 2 > 1.44
7 > 0.00, 1 > 0.68, 5 > 1.36
สามารถใส่คีย์เวิร์ดเพิ่มเติมได้แก่
- n_neighbors จำนวนเพื่อนบ้านที่จะให้คืนค่ากลับมา หากไม่ใส่จะคืนเท่ากับค่า n_neighbors ที่กำหนดให้ตั้งแต่ตอนแรก
- return_distance ถ้าใส่เป็น 0 จะไม่คืนค่าระยะทางกลับมา แต่จะคืนแค่อย่างเดียวคือดัชนีของจุด
ลองใส่ดู
print(knn.kneighbors(X,n_neighbors=8,return_distance=0))[[0 5 6 1 3 7 4 2]
[1 7 3 5 6 0 2 4]
[2 6 3 1 0 4 7 5]
[3 6 1 7 2 0 5 4]
[4 0 6 5 2 3 1 7]
[5 0 7 1 3 6 4 2]
[6 3 2 1 0 5 7 4]
[7 1 5 3 0 6 2 4]].kneighbors_graph
จะคืนค่าที่แสดงว่าตัวไหนเป็นเพื่อนบ้านของตัวนั้นบ้าง
เพียงแต่ว่าผลที่ได้จะอยู่ในรูปของ sparse matrix ดังนั้นเพื่อให้เห็นชัดสามารถแปลงเป็นอาเรย์ธรรมดาได้โดยเมธอด .toarray อีกที
print(type(knn.kneighbors_graph(X))) # ให้แสดงชนิด
print(knn.kneighbors_graph(X).toarray()) # แปลงเป็นอาเรย์ธรรมดาได้
<class 'scipy.sparse.csr.csr_matrix'>
[[ 1. 0. 0. 0. 0. 1. 1. 0.]
[ 0. 1. 0. 1. 0. 0. 0. 1.]
[ 0. 0. 1. 1. 0. 0. 1. 0.]
[ 0. 1. 0. 1. 0. 0. 1. 0.]
[ 1. 0. 0. 0. 1. 0. 1. 0.]
[ 1. 0. 0. 0. 0. 1. 0. 1.]
[ 0. 0. 1. 1. 0. 0. 1. 0.]
[ 0. 1. 0. 0. 0. 1. 0. 1.]]ถ้าใส่คีย์เวิร์ด mode='distance' ลงไปจะคืนค่าเป็นระยะทางแทน แล้วก็มีคีย์เวิร์ด n_neighbors สามารถเปลี่ยนจำนวนเพื่อนบ้านที่พิจารณาได้ด้วย
ตัวอย่าง
print(knn.kneighbors_graph(X,mode='distance',n_neighbors=8).toarray())ได้
[[ 0. 2.00350493 3.21293728 2.07395977 2.24451596 1.12763922
1.91394086 2.23635633]
[ 2.00350493 0. 3.12214116 1.16141094 4.05546124 1.46770732
1.80934825 0.68420112]
[ 3.21293728 3.12214116 0. 1.9628876 3.45228072 3.83210647
1.43561929 3.80417203]
[ 2.07395977 1.16141094 1.9628876 0. 3.58705789 2.16656867
0.77421595 1.84527381]
[ 2.24451596 4.05546124 3.45228072 3.58705789 0. 3.35721827
2.95862282 4.43043208]
[ 1.12763922 1.46770732 3.83210647 2.16656867 3.35721827 0.
2.40100554 1.35891489]
[ 1.91394086 1.80934825 1.43561929 0.77421595 2.95862282 2.40100554
0. 2.46612122]
[ 2.23635633 0.68420112 3.80417203 1.84527381 4.43043208 1.35891489
2.46612122 0. ]].predict_proba
เป็นการคำนวณความน่าจะเป็นว่าจะอยู่กลุ่มไหน แทนที่จะทำนายชัดลงไปเลยว่าอยู่กลุ่มไหน
ค่าความน่าจะเป็นในที่นี่คล้ายกับในการถดถอยโลจิสติก แต่ต่างกันตรงที่วิธีการคำนวณ
ตัวอย่างเทียบระหว่าง predict กับ predict_proba โดยจะเทียบให้เห็นด้วยว่าค่าจำนวนเพื่อนบ้านต่างกันก็มีความละเอียดในการแบ่งเขตทำนายที่ต่างกัน
X,z = datasets.make_blobs(n_samples=200,centers=2,cluster_std=2.5,random_state=12)
nmesh = 200
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),nmesh),np.linspace(X[:,1].min(),X[:,1].max(),nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
for i in [0,1]:
n = 3+27*i
knn = Knn(n)
knn.fit(X,z)
k = knn.kneighbors(X)
for j in [0,1]:
if(j==1):
mz = knn.predict_proba(mX)[:,1].reshape(nmesh,nmesh)
else:
mz = knn.predict(mX).reshape(nmesh,nmesh)
plt.subplot(221+i+2*j,xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()],aspect=1)
plt.scatter(X[:,0],X[:,1],10,c=z,edgecolor='k',cmap='winter')
plt.contourf(mx,my,mz,100,cmap='winter',zorder=0)
if(j==0):
plt.title('n=%d'%n)
else:
plt.ylabel('proba')
plt.show()
โดยรวมแล้วถือว่า sklearn สามารถใช้งานได้อย่างสะดวกดีมาก
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn