วิเคราะห์การถดถอยโลจิสติกด้วย sklearn
เขียนเมื่อ 2017/10/10 07:31
แก้ไขล่าสุด 2022/07/21 15:15
ก่อนหน้านี้ได้เขียนบทความแนะนำเกี่ยวกับการสร้างคลาสแบบจำลองการถดถอยโลจิสติกเพื่อวิเคราะห์จัดข้อมูลเป็นหมวดหมู่มามากมาย ซึ่งได้สรุปรวบยอดไว้ใน https://phyblas.hinaboshi.com/20171006
อย่างไรก็ตามในความเป็นจริงเราอาจไม่จำเป็นต้องศึกษารายละเอียดมากมายขนาดนั้นเพื่อที่จะใช้งานการถดถอยโลจิสติกก็ได้
เหมือนกับที่คนขับรถไม่จำเป็นต้องเข้าใจกลไกการทำงานภายในของรถ ไม่ต้องรู้ว่าทำไมหมุนพวงมาลัยแล้วรถถึงเลี้ยว ทำไมเหยียบเบรกแล้วรถหยุด แค่เข้าใจว่าขับยังไงก็พอแล้ว
แต่นั่นหมายความว่าต้องมีคนที่มีความรู้ความเข้าใจการทำงานภายในเป็นอย่างดีได้สร้างระบบอะไรบางอย่างให้คนทั่วไปใช้ได้และมีการเขียนคู่มือบอกไว้เป็นอย่างดี
เรื่องของการเขียนโปรแกรมก็เช่นเดียวกัน หากแค่ต้องการใช้งานแบบผิวเผินแล้วจะใช้มอดูลที่คนเตรียมเอาไว้เลยโดยไม่ต้องเข้าใจอะไรภายในก็ได้
มอดูล sklearn ได้เตรียมแบบจำลองต่างๆสำหรับการวิเคราะห์ต่างๆในการเรียนรู้ของเครื่องไว้มาก ใช้งานง่ายถึงขนาดที่ผู้ที่ไม่มีความรู้เรื่องพวกนี้มาก่อนก็สามารถใช้งานได้
สำหรับการถดถอยโลจิสติกนั้นสามารถใช้คลาสชื่อ LogisticRegression ใน sklearn.linear_model
หากต้องการแบ่งข้อมูลเป็นหมวดหมู่สามารถใช้คลาสนี้จัดการได้ทันที
การใช้งานเบื้องต้น
ตัวอย่างเช่นมีข้อมูลกลุ่มก้อนแบบในรูปนี้
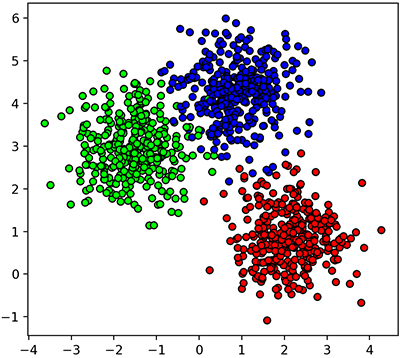
โค้ดที่ใช้สร้างข้อมูลและวาดภาพเป็นดังนี้ (คำอธิบายฟังก์ชัน make_blobs ที่ใช้สร้างอยู่ใน https://phyblas.hinaboshi.com/20161127)
ในที่นี้ z คือเลขกลุ่ม โดยเลข 0 คือสีน้ำเงิน เลข 1 คือสีแดง เลข 2 คือสีเขียว
จากนั้นต้องการใช้การวิเคราะห์การถดถอยโลจิสติกเพื่อแบ่งก็เขียนได้ดังนี้
ในที่นี้ขอย่อคลาส LogisticRegression เป็นสั้นๆเหลือแค่ Lori
เริ่มจากสร้างออบเจ็กต์จากคลาสขึ้น จากนั้นก็ใช้เมธอด fit ป้อนข้อมูลให้แบบจำลองนี้ไปทำการเรียนรู้
พอเรียนรู้เสร็จ คราวนี้ออบเจ็กต์แบบจำลองของเราก็พร้อมที่จะไปใช้เพื่อทำนายแบ่งกลุ่มของข้อมูลต่อไปแล้ว
จากนั้นขั้นต่อไปก็คือใช้เมธอด predict ซึ่งเป็นการให้แบบจำลองที่เรียนรู้แล้วมาทำนายผลให้เรา
เช่นอยากรู้ว่าจุด (0.1,0.2) จะถูกจัดอยู่ในกลุ่มไหนก็แค่พิมพ์
แบบนี้แสดงว่าตำแหน่งนั้นถูกจัดกลุ่มเป็นกลุ่ม 1 ก็คือสีแดง
ให้ระวังว่าอาเรย์ที่ใส่จำเป็นต้องเป็นอาเรย์สองมิติ แม้ว่าจะต้องการทำนายแค่จุดเดียวก็ตาม เพราะโดยทั่วไปแล้วเรามักจะให้ทำนายหลายจุดพร้อมกัน ซึ่งจะใช้งานสะดวกมาก
เช่น ลองพิจารณา ๕ จุดทีเดียวพร้อมกัน แล้วก็วาดรูปแสดงตำแหน่งพร้อมแสดงสีตามที่ทายได้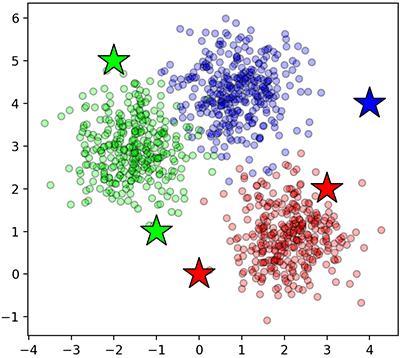
ในที่นี้ดาวคือจุดที่ทาย จะเห็นว่าสีดาวที่ได้สัมพันธ์กับสีของจุดที่อยู่ใกล้
คราวนี้เพื่อให้เห็นภาพชัดลองให้แบบจำลองทำการทำนายจุดบริเวณรอบๆ
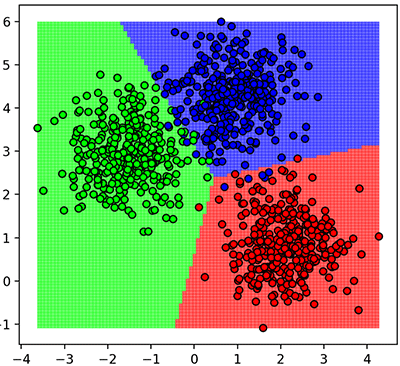
สามารถสรุปง่ายๆว่าขั้นตอนการใช้งานหลักๆก็คือ
1. สร้างออบเจ็กต์จากคลาส LogisticRegression (ในที่นี้ย่อเป็น Lori)
2. นำออบเจ็กต์ที่ได้มาใช้เมธอด fit เพื่อทำการเรียนรู้ข้อมูลที่ป้อนเข้าไป
3. ทำนายหมวดหมู่ของจุดที่ต้องการโดยใช้เมธอด predict
การทำนายเอาผลแบบละเอียดด้วย predict_proba
นอกจากการใช้งานเบื้องต้นที่ว่ามาแล้วในนี้ยังมีเมธอดที่น่าใช้งานอยู่อีกหลายตัว
เช่น predict_proba ซึ่งเอาไว้คำนวณความน่าจะเป็นในการถูกจัดเป็นแต่ละกลุ่ม
ปกติถ้าใช้ pridict เฉยๆจะเป็นการทำนายหากลุ่มที่มีความน่าจะเป็นสูงสุด แต่ถ้า predict_proba จะแยกออกมาชัดเลยว่ากลุ่มไหนมีความน่าจะเป็นเท่าไหร่ มีประโยชน์เวลาจะแยกวิเคราะห์ให้เห็นชัด
ตัวอย่างการใช้ ลองนำแบบจำลองอันเดิมมาใช้ predict_proba แทน แล้ววาดแสดงความน่าจะเป็นแยกแต่ละกลุ่ม และสุดท้ายเอามาวาดรวมกัน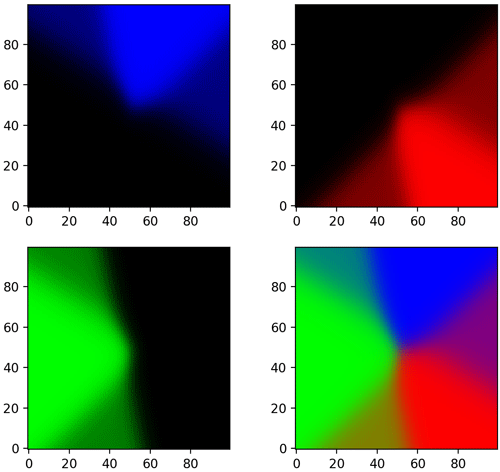
ในภาพนี้ถ้าส่วนไหนเป็นสีอะไรมากก็มีโอกาสเป็นกลุ่มนั้นสูงมาก บริเวณที่เป็นสีผสมนั้นมีความก้ำกึ่ง แต่เวลาต้องทายผลออกมาให้ชัดว่ากลุ่มไหนก็ตัดสินที่ว่ามีความเป็นสีไหนมากกว่า ก็คือมีค่าความน่าจะเป็นมากกว่า ก็จะตัดสินว่าเป็นกลุ่มนั้น
หากใช้ argmax(1) กับ predict_proba ก็จะได้ผลเป็นเท่ากับ predict
ลองตรวจสอบดูได้
นอกจากนี้ยังมีเมธอด predict_log_proba ซึ่งจะให้ค่าเป็นค่า log ของ predict_proba
การเอาค่าน้ำหนักและไบแอสที่เรียนรู้ได้มา
ค่าพารามิเตอร์น้ำหนักและไบแอสที่คำนวณได้จากในนี้จะถูกเก็บไว้ในแอตทริบิวต์ coef_ และ intercept_
โดย coef_ คือค่าน้ำหนัก เป็นอาเรย์สองมิติ ส่วน intercept_ คือค่าไบแอส เป็นอาเรย์มิติเดียว
ลองดู
พารามิเตอร์นี้เองที่จะถูกใช้เวลาที่ทำนายผล
เช่น predict_z = lori.predict(X) นั้นที่จริงแล้วหากจะเขียนคำนวณเองก็สามารถเขียนเป็น
คำนวณคะแนนความแม่นด้วย score
ปกติเวลาจะทดสอบประสิทธิภาพของผลการเรียนรู้ วิธีที่ง่ายก็คือดูว่าทายถูกมากแค่ไหน ซึ่งอาจคำนวณคะแนนความแม่นได้ง่ายๆโดย
จะได้คะแนนความแม่นซึ่งถ้าหากถูกหมดจะเป็นค่า 1 ถ้าผิดหมดจะเป็น 0
แต่ว่าในคลาส LogisticRegression นั้นได้เตรียมเมธอดสำหรับคำนวณตรงนี้ไว้ได้ง่ายๆ คือเมธอด score กล่าวคือสามารถเขียนแทนได้โดย
X และ z ที่เราใช้ในครั้งนี้คือข้อมูลที่ใช้ฝึกนั่นเอง ดังนั้นจึงได้ออกมาแม่น ผลการคำนวณพบว่าได้คะแนนความแม่นยำเป็น 0.98
ที่ไม่ได้คะแนนเต็มเพราะข้อมูลมีการปะปนกัน มีบางส่วนที่ล้ำไปอยู่ในวงล้อมของกลุ่มอื่น จึงไม่มีทางทายถูกได้หมด ดังที่จะเห็นได้จากในรูปข้างบนที่แสดงการแบ่งเขต จุดเขียวไม่ได้อยู่ในพื้นที่สีเขียวทั้งหมด จุดแดงจุดน้ำเงินก็เช่นกัน
การปรับไฮเพอร์พารามิเตอร์
ไฮเพอร์พารามิเตอร์คือค่าที่เป็นตัวกำหนดคุณสมบัติของแบบจำลองของเรา ปกติเป็นสิ่งที่เราต้องกำหนดใส่ลงไปเอง แต่ว่าใน sklearn นั้นไฮเพอร์พารามิเตอร์ทั้งหมดล้วนมีค่าตั้งต้น ถ้าเราสร้างขึ้นมาโดยไม่ได้กำหนดอะไรเลยก็จะเป็นการใช้ค่าตั้งต้นนั้น
เราสามารถดูค่าไฮเพอร์พารามิเตอร์ทั้งหมดได้โดยแค่สั่ง print ตัวออบเจ็กต์นั้น
เช่น
ได้
หรือถ้าใช้เมธอด get_params ก็จะได้ค่าพารามิเตอร์ทั้งหมดมาในรูปดิกชันนารี
ได้
จะเห็นว่ามีค่าอะไรต่างๆเยอะมากที่สามารถปรับแต่งได้ ซึ่งในขั้นตอนการสร้างออบเจ็กต์เราสามารใส่คีย์เวิร์ดเพื่อเปลี่ยนแปลงพวกไฮเพอร์พารามิเตอร์ต่างๆเหล่านี้
เนื่องจากมีรายละเอียดเยอะจะขอยกมาพูดถึงแค่ส่วนเดียว ในที่นี้ขอยกตัวอย่างเป็นเรื่องของไฮเพอร์พารามิเตอร์ที่เกี่ยวกับการเรกูลาไรซ์
ค่าที่เกี่ยวข้องกับเรกูลาไรซ์คือ penalty และ C
เรื่องเกี่ยวกับเรกูลาไรซ์ได้เขียนถึงไว้แล้วใน https://phyblas.hinaboshi.com/20170928
เพียงแต่ว่ามีส่วนแตกต่างที่ต้องเสริมสักหน่อย คือค่า C ในที่นี้เป็นส่วนกลับของค่า λ ที่อธิบายในนั้น กล่าวคือ C=1/λ หมายความว่า C ยิ่งน้อยยิ่งเรกูลาไรซ์แรง หากไม่ต้องการให้ไม่มีการเรกูลาไรซ์ก็ต้องปรับ C เป็นค่าสูงมากๆ
ส่วน penalty คือชนิดของการเรกูลาไรซ์ เลือกได้ระหว่าง l1 และ l2 ค่าตั้งต้นคือ l2
เนื่องจากค่า C เป็นส่วนกลับของ λ ดังนั้น C ยิ่งน้อยก็จะยิ่งทำให้ค่าน้ำหนักถูกถ่วงให้ไม่สามารถสูงขึ้นได้มาก หากน้อยเกินไปก็จะทำให้การเรียนรู้ไม่คืบหน้าได้
ลองเขียนโปรแกรมที่เปรียบเทียบผลของค่า C ที่มีต่อความแม่นยำและค่าน้ำหนัก โดยตัวอย่างคราวนี้ยังใช้เป็นข้อมูลเดิม ซึ่งมีพารามิเตอร์น้ำหนักอยู่ ๖ ตัว เนื่องจากมีตัวแปรต้น ๒ ตัว (๒ มิติ) และเป็นการแบ่ง ๓ กลุ่ม เราจะลองมาดูว่าหากเปลี่ยนค่า C แล้วจะส่งผลต่อค่าพารามิเตอร์ที่ได้ยังไง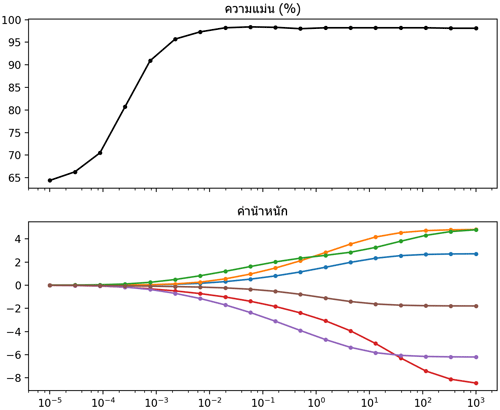
ผลที่ได้จะเห็นว่าค่า C ยิ่งสูง ค่าน้ำหนักแต่ละตัวก็สามารถไกลจาก 0 ได้มาก เกิดการกระจายค่ามากขึ้น แต่พอต่ำแล้วแต่ละค่าจะถูกบีบให้เข้าใกล้ 0
ส่วนเรื่องของความแม่นยำก็จะเห็นว่าถ้า C ต่ำจนถึงค่านึงความแม่นยำจะลด เพราะจะค่าน้ำหนักถูกหน่วงรั้งให้จำกัดอยู่ใกล้ 0 มากไปจนไม่เกิดผลในการเรียนรู้
ทั้งหมดนี้เป็นตัวอย่างส่วนหนึ่งของการใช้ LogisticRegression ของ sklearn
นอกจากนี้แล้วก็ยังมีรายละเอียดอีกมากมายที่ยังไม่ได้กล่าวถึง เช่นการปรับไฮเพอร์พารามิเตอร์ตัวอื่นๆ แล้วก็เมธอดอื่นๆ
รายละเอียดเพิ่มเติมอ่านต่อในเว็บคู่มือ sklearn
>> http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
LogisticRegression ของ sklearn ใช้งานได้สะดวกดี แม้คนที่ไม่ค่อยมีพื้นฐานเรื่องการเรียนรู้ของเครื่องเลยก็สามารถพอใช้งานได้
เพียงแต่หากรู้รายละเอียดมากขึ้นก็จะสามารถใช้งานได้อย่างเข้าใจขึ้น รู้ว่าปรับอะไรตรงไหนจะมีผลยังไง ถ้ามีปัญหาต้องแก้ยังไง จำเป็นต้องรู้มากแค่ไหนก็ขึ้นอยู่กับคน
เหมือนกับคนที่เป็นแต่ขับรถ พอวันนึงรถเกิดมีปัญหาขึ้นมาก็จะไม่สามารถไปต่อได้ ต้องรอให้คนที่รู้กลไกมาช่วยซ่อม
หากสนในรายละเอียดเรื่องการวิเคราะห์การถดถอยโลจิสติก สามารถอ่านบทความที่เขียนไว้ก่อนหน้านี้ได้
อย่างไรก็ตามในความเป็นจริงเราอาจไม่จำเป็นต้องศึกษารายละเอียดมากมายขนาดนั้นเพื่อที่จะใช้งานการถดถอยโลจิสติกก็ได้
เหมือนกับที่คนขับรถไม่จำเป็นต้องเข้าใจกลไกการทำงานภายในของรถ ไม่ต้องรู้ว่าทำไมหมุนพวงมาลัยแล้วรถถึงเลี้ยว ทำไมเหยียบเบรกแล้วรถหยุด แค่เข้าใจว่าขับยังไงก็พอแล้ว
แต่นั่นหมายความว่าต้องมีคนที่มีความรู้ความเข้าใจการทำงานภายในเป็นอย่างดีได้สร้างระบบอะไรบางอย่างให้คนทั่วไปใช้ได้และมีการเขียนคู่มือบอกไว้เป็นอย่างดี
เรื่องของการเขียนโปรแกรมก็เช่นเดียวกัน หากแค่ต้องการใช้งานแบบผิวเผินแล้วจะใช้มอดูลที่คนเตรียมเอาไว้เลยโดยไม่ต้องเข้าใจอะไรภายในก็ได้
มอดูล sklearn ได้เตรียมแบบจำลองต่างๆสำหรับการวิเคราะห์ต่างๆในการเรียนรู้ของเครื่องไว้มาก ใช้งานง่ายถึงขนาดที่ผู้ที่ไม่มีความรู้เรื่องพวกนี้มาก่อนก็สามารถใช้งานได้
สำหรับการถดถอยโลจิสติกนั้นสามารถใช้คลาสชื่อ LogisticRegression ใน sklearn.linear_model
หากต้องการแบ่งข้อมูลเป็นหมวดหมู่สามารถใช้คลาสนี้จัดการได้ทันที
การใช้งานเบื้องต้น
ตัวอย่างเช่นมีข้อมูลกลุ่มก้อนแบบในรูปนี้

โค้ดที่ใช้สร้างข้อมูลและวาดภาพเป็นดังนี้ (คำอธิบายฟังก์ชัน make_blobs ที่ใช้สร้างอยู่ใน https://phyblas.hinaboshi.com/20161127)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
np.random.seed(0)
X,z = datasets.make_blobs(n_samples=1000,n_features=2,centers=3,cluster_std=0.7)
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,s=30,edgecolor='k',cmap='brg')
plt.show()ในที่นี้ z คือเลขกลุ่ม โดยเลข 0 คือสีน้ำเงิน เลข 1 คือสีแดง เลข 2 คือสีเขียว
จากนั้นต้องการใช้การวิเคราะห์การถดถอยโลจิสติกเพื่อแบ่งก็เขียนได้ดังนี้
from sklearn.linear_model import LogisticRegression as Lori
lori = Lori()
lori.fit(X,z)ในที่นี้ขอย่อคลาส LogisticRegression เป็นสั้นๆเหลือแค่ Lori
เริ่มจากสร้างออบเจ็กต์จากคลาสขึ้น จากนั้นก็ใช้เมธอด fit ป้อนข้อมูลให้แบบจำลองนี้ไปทำการเรียนรู้
พอเรียนรู้เสร็จ คราวนี้ออบเจ็กต์แบบจำลองของเราก็พร้อมที่จะไปใช้เพื่อทำนายแบ่งกลุ่มของข้อมูลต่อไปแล้ว
จากนั้นขั้นต่อไปก็คือใช้เมธอด predict ซึ่งเป็นการให้แบบจำลองที่เรียนรู้แล้วมาทำนายผลให้เรา
เช่นอยากรู้ว่าจุด (0.1,0.2) จะถูกจัดอยู่ในกลุ่มไหนก็แค่พิมพ์
print(lori.predict(np.array([[0.1,0.2]]))) # ได้ [1]
แบบนี้แสดงว่าตำแหน่งนั้นถูกจัดกลุ่มเป็นกลุ่ม 1 ก็คือสีแดง
ให้ระวังว่าอาเรย์ที่ใส่จำเป็นต้องเป็นอาเรย์สองมิติ แม้ว่าจะต้องการทำนายแค่จุดเดียวก็ตาม เพราะโดยทั่วไปแล้วเรามักจะให้ทำนายหลายจุดพร้อมกัน ซึ่งจะใช้งานสะดวกมาก
เช่น ลองพิจารณา ๕ จุดทีเดียวพร้อมกัน แล้วก็วาดรูปแสดงตำแหน่งพร้อมแสดงสีตามที่ทายได้
X2 = np.array([[0,0.],[3,2.],[-1,1.],[4,4],[-2,5]])
z2 = lori.predict(X2)
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,s=30,alpha=0.3,edgecolor='k',cmap='brg')
plt.scatter(X2[:,0],X2[:,1],c=z2,s=700,marker='*',edgecolor='k',cmap='brg')
plt.show()
ในที่นี้ดาวคือจุดที่ทาย จะเห็นว่าสีดาวที่ได้สัมพันธ์กับสีของจุดที่อยู่ใกล้
คราวนี้เพื่อให้เห็นภาพชัดลองให้แบบจำลองทำการทำนายจุดบริเวณรอบๆ
nmesh = 100 # สร้างจุดที่จะให้ทำนาย เป็นตาราง 100x100 รอบบริเวณนี้
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),nmesh),
np.linspace(X[:,1].min(),X[:,1].max(),nmesh))
# ปรับให้เรียงต่อกันเป็นอาเรย์หนึ่งมิติ แล้วรวมค่า x และ y เข้าเป็นอาเรย์เดียว
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = lori.predict(mX) # ทำการทำนาย
mz = mz.reshape(nmesh,nmesh) # เปลี่ยนรูปกลับเป็นอาเรย์สองมิติ
plt.figure()
plt.axes(aspect=1)
plt.pcolormesh(mx,my,mz,alpha=0.6,cmap='brg') # วาดสีพื้น
plt.scatter(X[:,0],X[:,1],c=z,s=30,edgecolor='k',cmap='brg') # วาดจุดข้อมูล
plt.show()
สามารถสรุปง่ายๆว่าขั้นตอนการใช้งานหลักๆก็คือ
1. สร้างออบเจ็กต์จากคลาส LogisticRegression (ในที่นี้ย่อเป็น Lori)
2. นำออบเจ็กต์ที่ได้มาใช้เมธอด fit เพื่อทำการเรียนรู้ข้อมูลที่ป้อนเข้าไป
3. ทำนายหมวดหมู่ของจุดที่ต้องการโดยใช้เมธอด predict
การทำนายเอาผลแบบละเอียดด้วย predict_proba
นอกจากการใช้งานเบื้องต้นที่ว่ามาแล้วในนี้ยังมีเมธอดที่น่าใช้งานอยู่อีกหลายตัว
เช่น predict_proba ซึ่งเอาไว้คำนวณความน่าจะเป็นในการถูกจัดเป็นแต่ละกลุ่ม
ปกติถ้าใช้ pridict เฉยๆจะเป็นการทำนายหากลุ่มที่มีความน่าจะเป็นสูงสุด แต่ถ้า predict_proba จะแยกออกมาชัดเลยว่ากลุ่มไหนมีความน่าจะเป็นเท่าไหร่ มีประโยชน์เวลาจะแยกวิเคราะห์ให้เห็นชัด
ตัวอย่างการใช้ ลองนำแบบจำลองอันเดิมมาใช้ predict_proba แทน แล้ววาดแสดงความน่าจะเป็นแยกแต่ละกลุ่ม และสุดท้ายเอามาวาดรวมกัน
mz = lori.predict_proba(mX)
mz = mz.reshape(nmesh,nmesh,3)
plt.figure(figsize=[7,8])
zs = np.zeros([100,100])
plt.subplot(221) # กลุ่ม 0 สีน้ำเงิน
plt.imshow(np.stack([zs,zs,mz[:,:,0]],2),origin='lower')
plt.subplot(222) # กลุ่ม 1 สีแดง
plt.imshow(np.stack([mz[:,:,1],zs,zs],2),origin='lower')
plt.subplot(223) # กลุ่ม 2 สีเขียว
plt.imshow(np.stack([zs,mz[:,:,2],zs],2),origin='lower')
plt.subplot(224) # นำมารวมกัน
plt.imshow(np.stack([mz[:,:,1],mz[:,:,2],mz[:,:,0]],2),origin='lower')
plt.show()
ในภาพนี้ถ้าส่วนไหนเป็นสีอะไรมากก็มีโอกาสเป็นกลุ่มนั้นสูงมาก บริเวณที่เป็นสีผสมนั้นมีความก้ำกึ่ง แต่เวลาต้องทายผลออกมาให้ชัดว่ากลุ่มไหนก็ตัดสินที่ว่ามีความเป็นสีไหนมากกว่า ก็คือมีค่าความน่าจะเป็นมากกว่า ก็จะตัดสินว่าเป็นกลุ่มนั้น
หากใช้ argmax(1) กับ predict_proba ก็จะได้ผลเป็นเท่ากับ predict
ลองตรวจสอบดูได้
np.all(lori.predict_proba(X).argmax(1)==lori.predict(X)) # ได้ Trueนอกจากนี้ยังมีเมธอด predict_log_proba ซึ่งจะให้ค่าเป็นค่า log ของ predict_proba
การเอาค่าน้ำหนักและไบแอสที่เรียนรู้ได้มา
ค่าพารามิเตอร์น้ำหนักและไบแอสที่คำนวณได้จากในนี้จะถูกเก็บไว้ในแอตทริบิวต์ coef_ และ intercept_
โดย coef_ คือค่าน้ำหนัก เป็นอาเรย์สองมิติ ส่วน intercept_ คือค่าไบแอส เป็นอาเรย์มิติเดียว
ลองดู
print(lori.coef_)
print(lori.intercept_)[[ 1.39321745 2.54867122]
[ 2.49034169 -2.80449884]
[-4.41410752 -0.98528598]]
[-9.0248292 3.13710958 1.7673895 ]พารามิเตอร์นี้เองที่จะถูกใช้เวลาที่ทำนายผล
เช่น predict_z = lori.predict(X) นั้นที่จริงแล้วหากจะเขียนคำนวณเองก็สามารถเขียนเป็น
predict_z = (np.dot(X,lori.coef_.T)+lori.intercept_).argmax(1)คำนวณคะแนนความแม่นด้วย score
ปกติเวลาจะทดสอบประสิทธิภาพของผลการเรียนรู้ วิธีที่ง่ายก็คือดูว่าทายถูกมากแค่ไหน ซึ่งอาจคำนวณคะแนนความแม่นได้ง่ายๆโดย
khanaen = (lori.predict(X)==z).mean()จะได้คะแนนความแม่นซึ่งถ้าหากถูกหมดจะเป็นค่า 1 ถ้าผิดหมดจะเป็น 0
แต่ว่าในคลาส LogisticRegression นั้นได้เตรียมเมธอดสำหรับคำนวณตรงนี้ไว้ได้ง่ายๆ คือเมธอด score กล่าวคือสามารถเขียนแทนได้โดย
khanaen = lori.score(X,z)X และ z ที่เราใช้ในครั้งนี้คือข้อมูลที่ใช้ฝึกนั่นเอง ดังนั้นจึงได้ออกมาแม่น ผลการคำนวณพบว่าได้คะแนนความแม่นยำเป็น 0.98
ที่ไม่ได้คะแนนเต็มเพราะข้อมูลมีการปะปนกัน มีบางส่วนที่ล้ำไปอยู่ในวงล้อมของกลุ่มอื่น จึงไม่มีทางทายถูกได้หมด ดังที่จะเห็นได้จากในรูปข้างบนที่แสดงการแบ่งเขต จุดเขียวไม่ได้อยู่ในพื้นที่สีเขียวทั้งหมด จุดแดงจุดน้ำเงินก็เช่นกัน
การปรับไฮเพอร์พารามิเตอร์
ไฮเพอร์พารามิเตอร์คือค่าที่เป็นตัวกำหนดคุณสมบัติของแบบจำลองของเรา ปกติเป็นสิ่งที่เราต้องกำหนดใส่ลงไปเอง แต่ว่าใน sklearn นั้นไฮเพอร์พารามิเตอร์ทั้งหมดล้วนมีค่าตั้งต้น ถ้าเราสร้างขึ้นมาโดยไม่ได้กำหนดอะไรเลยก็จะเป็นการใช้ค่าตั้งต้นนั้น
เราสามารถดูค่าไฮเพอร์พารามิเตอร์ทั้งหมดได้โดยแค่สั่ง print ตัวออบเจ็กต์นั้น
เช่น
lori = Lori()
print(lori)ได้
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)หรือถ้าใช้เมธอด get_params ก็จะได้ค่าพารามิเตอร์ทั้งหมดมาในรูปดิกชันนารี
lori.get_params()ได้
{'C': 1.0,
'class_weight': None,
'dual': False,
'fit_intercept': True,
'intercept_scaling': 1,
'max_iter': 100,
'multi_class': 'ovr',
'n_jobs': 1,
'penalty': 'l2',
'random_state': None,
'solver': 'liblinear',
'tol': 0.0001,
'verbose': 0,
'warm_start': False}จะเห็นว่ามีค่าอะไรต่างๆเยอะมากที่สามารถปรับแต่งได้ ซึ่งในขั้นตอนการสร้างออบเจ็กต์เราสามารใส่คีย์เวิร์ดเพื่อเปลี่ยนแปลงพวกไฮเพอร์พารามิเตอร์ต่างๆเหล่านี้
เนื่องจากมีรายละเอียดเยอะจะขอยกมาพูดถึงแค่ส่วนเดียว ในที่นี้ขอยกตัวอย่างเป็นเรื่องของไฮเพอร์พารามิเตอร์ที่เกี่ยวกับการเรกูลาไรซ์
ค่าที่เกี่ยวข้องกับเรกูลาไรซ์คือ penalty และ C
เรื่องเกี่ยวกับเรกูลาไรซ์ได้เขียนถึงไว้แล้วใน https://phyblas.hinaboshi.com/20170928
เพียงแต่ว่ามีส่วนแตกต่างที่ต้องเสริมสักหน่อย คือค่า C ในที่นี้เป็นส่วนกลับของค่า λ ที่อธิบายในนั้น กล่าวคือ C=1/λ หมายความว่า C ยิ่งน้อยยิ่งเรกูลาไรซ์แรง หากไม่ต้องการให้ไม่มีการเรกูลาไรซ์ก็ต้องปรับ C เป็นค่าสูงมากๆ
ส่วน penalty คือชนิดของการเรกูลาไรซ์ เลือกได้ระหว่าง l1 และ l2 ค่าตั้งต้นคือ l2
เนื่องจากค่า C เป็นส่วนกลับของ λ ดังนั้น C ยิ่งน้อยก็จะยิ่งทำให้ค่าน้ำหนักถูกถ่วงให้ไม่สามารถสูงขึ้นได้มาก หากน้อยเกินไปก็จะทำให้การเรียนรู้ไม่คืบหน้าได้
ลองเขียนโปรแกรมที่เปรียบเทียบผลของค่า C ที่มีต่อความแม่นยำและค่าน้ำหนัก โดยตัวอย่างคราวนี้ยังใช้เป็นข้อมูลเดิม ซึ่งมีพารามิเตอร์น้ำหนักอยู่ ๖ ตัว เนื่องจากมีตัวแปรต้น ๒ ตัว (๒ มิติ) และเป็นการแบ่ง ๓ กลุ่ม เราจะลองมาดูว่าหากเปลี่ยนค่า C แล้วจะส่งผลต่อค่าพารามิเตอร์ที่ได้ยังไง
ccc = 10**np.linspace(-5,3,18)
coef = []
sco = []
for C in ccc:
lori = Lori(C=C)
lori.fit(X,z)
sco.append(lori.score(X,z)*100)
coef.append(lori.coef_.ravel())
plt.subplot(211,xscale='log')
plt.title(u'ความแม่น (%)',family='Tahoma')
plt.tick_params(labelbottom='off')
plt.plot(ccc,sco,'k.-')
plt.subplot(212,xscale='log')
plt.title(u'ค่าน้ำหนัก',family='Tahoma')
plt.plot(ccc,coef,'.-')
plt.show()
ผลที่ได้จะเห็นว่าค่า C ยิ่งสูง ค่าน้ำหนักแต่ละตัวก็สามารถไกลจาก 0 ได้มาก เกิดการกระจายค่ามากขึ้น แต่พอต่ำแล้วแต่ละค่าจะถูกบีบให้เข้าใกล้ 0
ส่วนเรื่องของความแม่นยำก็จะเห็นว่าถ้า C ต่ำจนถึงค่านึงความแม่นยำจะลด เพราะจะค่าน้ำหนักถูกหน่วงรั้งให้จำกัดอยู่ใกล้ 0 มากไปจนไม่เกิดผลในการเรียนรู้
ทั้งหมดนี้เป็นตัวอย่างส่วนหนึ่งของการใช้ LogisticRegression ของ sklearn
นอกจากนี้แล้วก็ยังมีรายละเอียดอีกมากมายที่ยังไม่ได้กล่าวถึง เช่นการปรับไฮเพอร์พารามิเตอร์ตัวอื่นๆ แล้วก็เมธอดอื่นๆ
รายละเอียดเพิ่มเติมอ่านต่อในเว็บคู่มือ sklearn
>> http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
LogisticRegression ของ sklearn ใช้งานได้สะดวกดี แม้คนที่ไม่ค่อยมีพื้นฐานเรื่องการเรียนรู้ของเครื่องเลยก็สามารถพอใช้งานได้
เพียงแต่หากรู้รายละเอียดมากขึ้นก็จะสามารถใช้งานได้อย่างเข้าใจขึ้น รู้ว่าปรับอะไรตรงไหนจะมีผลยังไง ถ้ามีปัญหาต้องแก้ยังไง จำเป็นต้องรู้มากแค่ไหนก็ขึ้นอยู่กับคน
เหมือนกับคนที่เป็นแต่ขับรถ พอวันนึงรถเกิดมีปัญหาขึ้นมาก็จะไม่สามารถไปต่อได้ ต้องรอให้คนที่รู้กลไกมาช่วยซ่อม
หากสนในรายละเอียดเรื่องการวิเคราะห์การถดถอยโลจิสติก สามารถอ่านบทความที่เขียนไว้ก่อนหน้านี้ได้
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn