[python] นำต้นไม้ตัดสินใจหลายต้นมารวมกันเป็นป่าสุ่ม
เขียนเมื่อ 2017/11/11 00:05
แก้ไขล่าสุด 2022/07/21 15:04
ก่อนหน้านี้ได้แนะนำต้นไม้ตัดสินใจ (决策树, decision tree) ไปแล้วใน https://phyblas.hinaboshi.com/20171105
ต้นไม้ตัดสินใจนั้นไวต่อการสุ่มกลุ่มข้อมูล ดังนั้นหากแค่เปลี่ยนชุดข้อมูลเพียงเล็กน้อยผลการแบ่งที่ได้ก็อาจแตกต่างไปจากเดิมมากเลยก็เป็นได้
ดังนั้นจึงอาจทำให้เกิดการเรียนรู้เกิน (过学习, over-learning) ได้ง่าย คือเวลาที่ให้ต้นไม้เรียนรู้แล้วแตกกิ่งย่อยจนกว่าจะแบ่งข้อมูลที่ให้ไปจนทายได้ถูกหมด พอนำไปใช้กับข้อมูลที่ไม่ได้อยู่ในกลุ่มนี้ก็อาจจะทายไม่ถูกเลยก็ได้
จึงมีคนคิดวิธีการที่สร้างต้นไม้ตัดสินใจหลายๆต้นโดยใช้ข้อมูลที่ต่างกัน แล้วนำผลจากหลายต้นนั้นมารวมกัน วิธีนี้ถูกเรียกว่า ป่าสุ่ม (随机森林, random forest)
นั่นเพราะถ้าต้นไม้มาอยู่รวมกันหลายๆต้นมันก็จะกลายเป็นป่าขึ้นมา และเป็นป่าของต้นไม้ที่เกิดจากการสุ่ม ก็เลยเรียกว่าเป็นป่าสุ่ม
หลักการของป่าสุ่มก็คือสุ่มข้อมูลจากกลุ่มข้อมูลที่จะใช้ในการเรียนรู้ขึ้นมาหลายๆรอบ โดยทั่วไปแล้วจะใช้การสุ่มแบบบู๊ตสแตร็ป (bootstrap)
บู๊ตสแตร็ปคือการสุ่มแบบที่สามารถเลือกซ้ำได้ เช่น หากเราทำการสุ่มหยิบสลากที่มีเลข 0-19 อยู่มาทั้งหมด 20 ครั้ง โดยแต่ละครั้งหยิบคืนกลับที่เดิม อาจเขียนในไพธอนได้โดยใช้คำสั่ง random.choice ใน numpy ดังนี้
ได้
จะเห็นว่าในแต่ละรอบอาจมีบางตัวถูกหยิบซ้ำ แล้วบางตัวก็ไม่ถูกเลือกเลย ดังนั้นในแต่ละรอบเราจะได้ตัวอย่างไม่ซ้ำกันมาใช้ป้อนให้กับต้นไม้
จากนั้นเราก็เอาข้อมูลที่สุ่มได้นี้มาสร้างต้นไม้ต้นหนึ่ง เสร็จแล้วก็สุ่มแบบเดิมอีกครั้ง สร้างต้นไม้อีกต้น ทำแบบนี้ไปเรื่อยๆ
จะลองสร้างทั้งหมดกี่ต้นก็ได้ สุดท้ายแล้วก็เอาผลการทายของทุกต้นมาเทียบกัน ทำการโหวตว่าผลการทายอันไหนถูกโหวตมากที่สุด ก็เลือกคำตอบนั้นมาเป็นคำตอบสุดท้าย
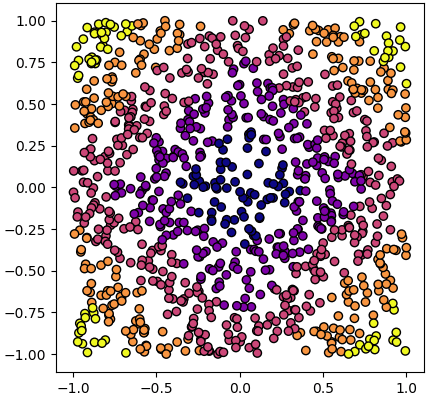
เช่น ยกตัวอย่าง ลองพยายามที่จะแบ่งข้อมูลชุดนี้ ซึ่งมีอยู่ ๕ กลุ่ม
โค้ดเป็นดังนี้
เราจะลองวนซ้ำทั้งหมด 10 รอบ ระหว่างนั้นก็เก็บผลลัพธ์ในแต่ละรอบที่แปลงเป็นแบบ one-hot ไปด้วย แล้วสุดท้ายก็นำมาสรุปเป็นผลโหวต หาผลสรุปรวม
ได้
จะเห็นว่าแม้แต่ละรอบจะทายถูกได้ไม่ถึง 0.9 เลย แต่พอนำมาโหวตรวมกันกลับได้สูงกว่า 0.9
อีกทั้งหากเราลองดูคำตอบของการใช้ต้นไม้ตัดสินใจต้นเดียวจากข้อมูลทั้งหมด ก็พบว่าไม่สูงเท่านั้น
ดังนั้นจะเห็นได้ว่าการสุ่มข้อมูลเพื่อสร้างต้นไม้หลายต้นแล้วโหวต ได้ผลดีกว่าการนำข้อมูลทั้งหมดมาสร้างต้นไม้ทีเดียว
อนึ่ง ถ้าหากลองดูรูปเทียบหน้าตาการแบ่งแล้วจะเห็นเป็นแบบนี้
นี่คือการแบ่งของต้นไม้ตัดสินใจต้นเดียว
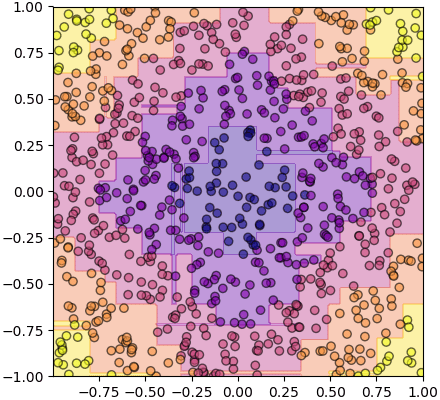
ส่วนนี่คือป่าสุ่มซึ่งได้จากต้นไม้ ๑๐ ต้น
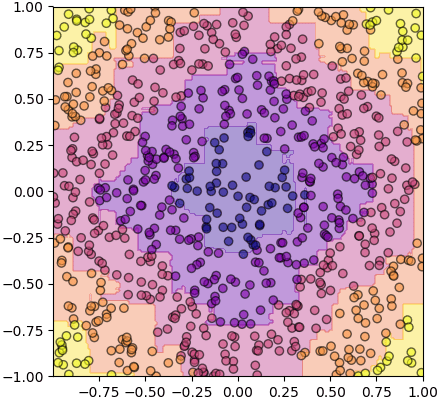
จะเห็นว่าหน้าตาออกมาดูดีกว่าหน่อย เส้นแบ่งดูมีความละเอียดมากขึ้น
โดยทั่วไปแล้วยิ่งเพิ่มจำนวนต้นไม้ในป่ามากก็จะยิ่งดี แต่เวลาที่ใช้คำนวณก็จะเพิ่มสูงขึ้นตาม
การนำเอาตัวทำนายหลายตัวมารวมกันแล้วคิดผลร่วมกันแบบนี้ถูกเรียกรวมๆว่าวิธีการอ็องซ็องบล์ (ensemble) นอกจากป่าสุ่มแล้วยังมีวิธีการอ็องซ็องบล์อยู่อีกหลายแบบ
จากนั้นก็ขอสรุปรวมเป็นคลาสไว้แบบนี้ โดยในที่นี้จะใช้คลาสของต้นไม้ตัดสินใจที่สร้างไว้คราวก่อนมาเป็นส่วนประกอบด้วย แทนที่จะใช้ของ sklearn จะได้เป็นการสร้างเองทั้งหมด แต่ที่จริงจะใช้ต้นไม้ตัดสินใจของ sklearn ก็ทำได้คล้ายๆกัน
พอเขียนแบบนี้แล้วก็นำมาใช้ได้สะดวก
ในที่นี้เมธอด thamnai จะทำการทำนายคำตอบจากผลโหวต ส่วน thamnai_laiat จะทำนายความน่าจะเป็นของแต่ละคำตอบโดยดูจากจำนวนต้นไม้ที่ทาย
ตัวอย่างการลองนำมาใช้งานดู
พอสร้างเป็นคลาสแบบนี้แล้วก็จัดการอะไรได้ง่าย ภายในตัวป่าสุ่มจะประกอบไปด้วยต้นไม้ตัดสินใจอยู่ข้างใน ในที่นี้เก็บตัวออบเจ็กต์ต้นไม้ตัดสินใจเอาไว้ในลิสต์ซึ่งเป็นแอตทริบิวต์ชื่อ .tonmai สามารถลองไล่ล้วงดูองค์ประกอบด้านในได้
ต่อไปลองใช้การทำนายละเอียดเพื่อดูความเป็นไปได้ของการจำแนกสองกลุ่ม โดยสุ่มสร้างต้นไม้สักร้อยต้น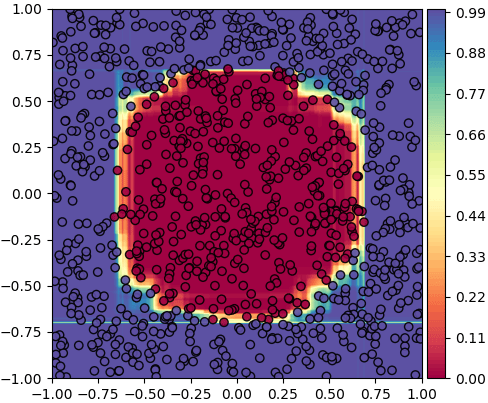
ส่วนไหนที่ต้นไม้ทุกต้นทายว่าเป็นกลุ่ม 0 เหมือนกันก็จะเป็นสีม่วง แต่ถ้าทายเป็นกลุ่ม 1 เหมือนกันหมดก็จะเป็นสีแดง ส่วนตรงรอยต่อที่มีบางต้นทายเป็น 0 บ้าง 1 บ้างก็จะเป็นสีระหว่างนั้น สัดส่วนแสดงตามแถบสีทางด้านขวา
เรื่องของป่าสุ่มนี้เป็นตัวอย่างที่แสดงให้เห็นว่าการร่วมแรงร่วมใจจะก่อให้เกิดพลังอันยิ่งใหญ่ได้ รวมกันเราอยู่ แยกหมู่เราขอบาย
จะเห็นว่าแม้ต้นไม้ต้นเดียวอาจจะไร้พลัง แต่พอรวมกันเป็นป่าก็จะดูมีคุณค่าขึ้นมา ดังนั้นเราควรจะมาช่วยกันปลูกป่าเพื่อโลกที่สดใสของพวกเรา
จากวันนี้สักหมื่นปี ต้นไม้ที่ท่านปลูก ต้องสวยต้องงดงาม และยิ่งใหญ่~
อ้างอิง
ต้นไม้ตัดสินใจนั้นไวต่อการสุ่มกลุ่มข้อมูล ดังนั้นหากแค่เปลี่ยนชุดข้อมูลเพียงเล็กน้อยผลการแบ่งที่ได้ก็อาจแตกต่างไปจากเดิมมากเลยก็เป็นได้
ดังนั้นจึงอาจทำให้เกิดการเรียนรู้เกิน (过学习, over-learning) ได้ง่าย คือเวลาที่ให้ต้นไม้เรียนรู้แล้วแตกกิ่งย่อยจนกว่าจะแบ่งข้อมูลที่ให้ไปจนทายได้ถูกหมด พอนำไปใช้กับข้อมูลที่ไม่ได้อยู่ในกลุ่มนี้ก็อาจจะทายไม่ถูกเลยก็ได้
จึงมีคนคิดวิธีการที่สร้างต้นไม้ตัดสินใจหลายๆต้นโดยใช้ข้อมูลที่ต่างกัน แล้วนำผลจากหลายต้นนั้นมารวมกัน วิธีนี้ถูกเรียกว่า ป่าสุ่ม (随机森林, random forest)
นั่นเพราะถ้าต้นไม้มาอยู่รวมกันหลายๆต้นมันก็จะกลายเป็นป่าขึ้นมา และเป็นป่าของต้นไม้ที่เกิดจากการสุ่ม ก็เลยเรียกว่าเป็นป่าสุ่ม

หลักการของป่าสุ่มก็คือสุ่มข้อมูลจากกลุ่มข้อมูลที่จะใช้ในการเรียนรู้ขึ้นมาหลายๆรอบ โดยทั่วไปแล้วจะใช้การสุ่มแบบบู๊ตสแตร็ป (bootstrap)
บู๊ตสแตร็ปคือการสุ่มแบบที่สามารถเลือกซ้ำได้ เช่น หากเราทำการสุ่มหยิบสลากที่มีเลข 0-19 อยู่มาทั้งหมด 20 ครั้ง โดยแต่ละครั้งหยิบคืนกลับที่เดิม อาจเขียนในไพธอนได้โดยใช้คำสั่ง random.choice ใน numpy ดังนี้
import numpy as np
print(np.random.choice(20,20))ได้
[ 0 14 0 0 16 12 3 5 9 5 15 13 18 6 5 1 5 6 2 13]จะเห็นว่าในแต่ละรอบอาจมีบางตัวถูกหยิบซ้ำ แล้วบางตัวก็ไม่ถูกเลือกเลย ดังนั้นในแต่ละรอบเราจะได้ตัวอย่างไม่ซ้ำกันมาใช้ป้อนให้กับต้นไม้
จากนั้นเราก็เอาข้อมูลที่สุ่มได้นี้มาสร้างต้นไม้ต้นหนึ่ง เสร็จแล้วก็สุ่มแบบเดิมอีกครั้ง สร้างต้นไม้อีกต้น ทำแบบนี้ไปเรื่อยๆ
จะลองสร้างทั้งหมดกี่ต้นก็ได้ สุดท้ายแล้วก็เอาผลการทายของทุกต้นมาเทียบกัน ทำการโหวตว่าผลการทายอันไหนถูกโหวตมากที่สุด ก็เลือกคำตอบนั้นมาเป็นคำตอบสุดท้าย
เช่น ยกตัวอย่าง ลองพยายามที่จะแบ่งข้อมูลชุดนี้ ซึ่งมีอยู่ ๕ กลุ่ม

โค้ดเป็นดังนี้
import matplotlib.pyplot as plt
np.random.seed(20)
X = np.random.uniform(-1,1,[1000,2])
z = ((np.abs(X[:,0])+np.abs(X[:,1]))//0.4).astype(int)
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='plasma')
plt.show()เราจะลองวนซ้ำทั้งหมด 10 รอบ ระหว่างนั้นก็เก็บผลลัพธ์ในแต่ละรอบที่แปลงเป็นแบบ one-hot ไปด้วย แล้วสุดท้ายก็นำมาสรุปเป็นผลโหวต หาผลสรุปรวม
from sklearn.tree import DecisionTreeClassifier as Ditri
from sklearn.model_selection import train_test_split
X_fuek,X_truat,z_fuek,z_truat = train_test_split(X,z,test_size=0.2) # แยกข้อมูลส่วนหนึ่งไว้ตรวตสอบ
zzz = 0 # เตรียมไว้สำหรับรวมผลของแต่ละรอบ
for i in range(10):
s = np.random.choice(800,800) # สุ่ม บูตสแตร็ป
dt = Ditri() # ใช้ต้นไม้ตัดสินใจของ sklearn
dt.fit(X_fuek[s],z_fuek[s]) # เรียนรู้ด้วยข้อมูลที่สุ่มได้ในแต่ละรอบ
zz = dt.predict(X_truat) # ทำนายผลของแต่ละรอบ
zz_1h = zz[:,None]==np.arange(10) # ทำผลเป็น one-hot
zzz += zz_1h # เก็บรวมผลของแต่ละรอบ
print(u'รอบที่ %d คะแนน %.3f'%(i+1,(zz==z_truat).mean()))
# นำผลการทำนายในแต่ละรอบมาสรุปรวมเป็นผลแล้วหาความแม่น
print('---\nผลรวมได้ %.3f'%(zzz.argmax(1)==z_truat).mean())ได้
รอบที่ 1 คะแนน 0.810
รอบที่ 2 คะแนน 0.845
รอบที่ 3 คะแนน 0.845
รอบที่ 4 คะแนน 0.870
รอบที่ 5 คะแนน 0.855
รอบที่ 6 คะแนน 0.835
รอบที่ 7 คะแนน 0.840
รอบที่ 8 คะแนน 0.885
รอบที่ 9 คะแนน 0.845
รอบที่ 10 คะแนน 0.890
---
ผลรวมได้ 0.935จะเห็นว่าแม้แต่ละรอบจะทายถูกได้ไม่ถึง 0.9 เลย แต่พอนำมาโหวตรวมกันกลับได้สูงกว่า 0.9
อีกทั้งหากเราลองดูคำตอบของการใช้ต้นไม้ตัดสินใจต้นเดียวจากข้อมูลทั้งหมด ก็พบว่าไม่สูงเท่านั้น
dt = Ditri()
dt.fit(X_fuek,z_fuek)
zz = dt.predict(X_truat)
print((zz==z_truat).mean()) # ได้ 0.89ดังนั้นจะเห็นได้ว่าการสุ่มข้อมูลเพื่อสร้างต้นไม้หลายต้นแล้วโหวต ได้ผลดีกว่าการนำข้อมูลทั้งหมดมาสร้างต้นไม้ทีเดียว
อนึ่ง ถ้าหากลองดูรูปเทียบหน้าตาการแบ่งแล้วจะเห็นเป็นแบบนี้
นี่คือการแบ่งของต้นไม้ตัดสินใจต้นเดียว

ส่วนนี่คือป่าสุ่มซึ่งได้จากต้นไม้ ๑๐ ต้น

จะเห็นว่าหน้าตาออกมาดูดีกว่าหน่อย เส้นแบ่งดูมีความละเอียดมากขึ้น
โดยทั่วไปแล้วยิ่งเพิ่มจำนวนต้นไม้ในป่ามากก็จะยิ่งดี แต่เวลาที่ใช้คำนวณก็จะเพิ่มสูงขึ้นตาม
การนำเอาตัวทำนายหลายตัวมารวมกันแล้วคิดผลร่วมกันแบบนี้ถูกเรียกรวมๆว่าวิธีการอ็องซ็องบล์ (ensemble) นอกจากป่าสุ่มแล้วยังมีวิธีการอ็องซ็องบล์อยู่อีกหลายแบบ
จากนั้นก็ขอสรุปรวมเป็นคลาสไว้แบบนี้ โดยในที่นี้จะใช้คลาสของต้นไม้ตัดสินใจที่สร้างไว้คราวก่อนมาเป็นส่วนประกอบด้วย แทนที่จะใช้ของ sklearn จะได้เป็นการสร้างเองทั้งหมด แต่ที่จริงจะใช้ต้นไม้ตัดสินใจของ sklearn ก็ทำได้คล้ายๆกัน
import numpy as np
import matplotlib.pyplot as plt
def gini(p):
return 1-(p**2).sum()
class Chuttaek:
def __init__(self,X,z,chan):
self.chan = chan
self.n = len(z)
self.king = []
if(len(np.unique(z))==1):
self.z = z[0]
elif(chan==0):
self.z = np.bincount(z).argmax()
else:
self.gn = 1
for j in range(X.shape[1]):
x = X[:,j]
xas = x.argsort()
x_riang = x[xas]
z_riang = z[xas]
x_kan = (x_riang[1:]+x_riang[:-1])/2
x_kan = x_kan[z_riang[1:]!=z_riang[:-1]]
for khabaeng in x_kan:
baeng = khabaeng>x
z_sai = z[baeng]
z_khwa = z[~baeng]
n_sai = float(len(z_sai))
n_khwa = float(len(z_khwa))
gn = (gini(np.bincount(z_sai)/n_sai)*n_sai+gini(np.bincount(z_khwa)/n_khwa)*n_khwa)/self.n
if(self.gn>gn):
self.gn = gn
self.j = j
self.khabaeng = khabaeng
o = (self.khabaeng>X[:,self.j])
self.king = [Chuttaek(X[o],z[o],chan-1),Chuttaek(X[~o],z[~o],chan-1)]
def __call__(self,X):
if(self.king==[]):
return self.z
else:
o = self.khabaeng>X[:,self.j]
return np.where(o,self.king[0](X),self.king[1](X))
class TonmaiTatsinchai:
def __init__(self,luek):
self.luek = luek
def rianru(self,X,z):
self.rak = Chuttaek(X,z,self.luek)
def thamnai(self,X):
return self.rak(X)
class Pasum:
def __init__(self,luek,n_tonmai=10):
self.luek = luek
self.n_tonmai = n_tonmai
def rianru(self,X,z):
n = len(z)
self.kiklum = z.max()+1
self.tonmai = []
for i in range(self.n_tonmai):
tt = TonmaiTatsinchai(self.luek)
s = np.random.choice(n,n)
tt.rianru(X[s],z[s])
self.tonmai.append(tt)
def _thamnai(self,X):
phon = 0
for tt in self.tonmai:
phon += tt.thamnai(X)[:,None]==np.arange(self.kiklum)
return phon
def thamnai(self,X):
return self._thamnai(X).argmax(1)
def thamnai_laiat(self,X):
return self._thamnai(X)/self.n_tonmaiพอเขียนแบบนี้แล้วก็นำมาใช้ได้สะดวก
ในที่นี้เมธอด thamnai จะทำการทำนายคำตอบจากผลโหวต ส่วน thamnai_laiat จะทำนายความน่าจะเป็นของแต่ละคำตอบโดยดูจากจำนวนต้นไม้ที่ทาย
ตัวอย่างการลองนำมาใช้งานดู
np.random.seed(2)
X = np.random.uniform(-1,1,[1000,2])
z = (np.sqrt(X[:,0]**2+X[:,1]**2)//0.282).astype(int)
pasum = Pasum(100)
pasum.rianru(X,z)
nmesh = 200
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),nmesh),np.linspace(X[:,1].min(),X[:,1].max(),nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = pasum.thamnai(mX).reshape(nmesh,nmesh)
plt.axes(aspect=1,xlim=[mx.min(),mx.max()],ylim=[my.min(),my.max()])
plt.scatter(X[:,0],X[:,1],alpha=0.6,c=z,edgecolor='k',cmap='rainbow')
plt.contourf(mx,my,mz,alpha=0.4,cmap='rainbow',zorder=0)
plt.show()
พอสร้างเป็นคลาสแบบนี้แล้วก็จัดการอะไรได้ง่าย ภายในตัวป่าสุ่มจะประกอบไปด้วยต้นไม้ตัดสินใจอยู่ข้างใน ในที่นี้เก็บตัวออบเจ็กต์ต้นไม้ตัดสินใจเอาไว้ในลิสต์ซึ่งเป็นแอตทริบิวต์ชื่อ .tonmai สามารถลองไล่ล้วงดูองค์ประกอบด้านในได้
print(len(pasum.tonmai)) # ได้ 10
print(pasum.tonmai[0]) # ได้ <__main__.TonmaiTatsinchai object at 0x1166a97b8>
print(pasum.tonmai[0].rak) # ได้ <__main__.Chuttaek object at 0x1166a9c18>
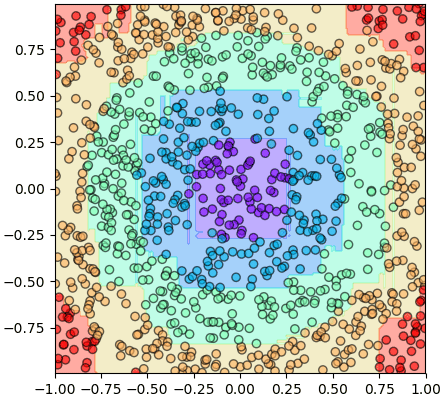
print(pasum.tonmai[0].rak.king) # ได้ [<__main__.Chuttaek object at 0x1166a99e8>, <__main__.Chuttaek object at 0x1165acc18>]ต่อไปลองใช้การทำนายละเอียดเพื่อดูความเป็นไปได้ของการจำแนกสองกลุ่ม โดยสุ่มสร้างต้นไม้สักร้อยต้น
np.random.seed(11)
X = np.random.uniform(-1,1,[1000,2])
z = (np.sqrt(X[:,0]**2+X[:,1]**2)//0.707).astype(int)
pasum = Pasum(100,n_tonmai=100)
pasum.rianru(X,z)
nmesh = 200
mx,my = np.meshgrid(np.linspace(-1,1,nmesh),np.linspace(-1,1,nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = pasum.thamnai_laiat(mX)[:,1].reshape(nmesh,nmesh)
plt.axes(aspect=1,xlim=[mx.min(),mx.max()],ylim=[my.min(),my.max()])
plt.scatter(X[:,0],X[:,1],c=z,alpha=0.9,edgecolor='k',cmap='Spectral')
plt.contourf(mx,my,mz,100,cmap='Spectral',zorder=0)
plt.colorbar(pad=0.01)
plt.show()
ส่วนไหนที่ต้นไม้ทุกต้นทายว่าเป็นกลุ่ม 0 เหมือนกันก็จะเป็นสีม่วง แต่ถ้าทายเป็นกลุ่ม 1 เหมือนกันหมดก็จะเป็นสีแดง ส่วนตรงรอยต่อที่มีบางต้นทายเป็น 0 บ้าง 1 บ้างก็จะเป็นสีระหว่างนั้น สัดส่วนแสดงตามแถบสีทางด้านขวา
เรื่องของป่าสุ่มนี้เป็นตัวอย่างที่แสดงให้เห็นว่าการร่วมแรงร่วมใจจะก่อให้เกิดพลังอันยิ่งใหญ่ได้ รวมกันเราอยู่ แยกหมู่เราขอบาย
จะเห็นว่าแม้ต้นไม้ต้นเดียวอาจจะไร้พลัง แต่พอรวมกันเป็นป่าก็จะดูมีคุณค่าขึ้นมา ดังนั้นเราควรจะมาช่วยกันปลูกป่าเพื่อโลกที่สดใสของพวกเรา
จากวันนี้สักหมื่นปี ต้นไม้ที่ท่านปลูก ต้องสวยต้องงดงาม และยิ่งใหญ่~
อ้างอิง
https://www.amazon.co.jp/Python機械学習プログラミング-達人データサイエンティストによる理論と実践-impress-top-gearシリーズ-ebook/dp/B01HGIPIAK
https://qiita.com/yshi12/items/6d30010b353b084b3749
http://www.oschina.net/translate/random-forests-in-python
https://qiita.com/deaikei/items/52d84ccfedbfc3b222cb
https://qiita.com/mshinoda88/items/8bfe0b540b35437296bd
https://qiita.com/yshi12/items/6d30010b353b084b3749
http://www.oschina.net/translate/random-forests-in-python
https://qiita.com/deaikei/items/52d84ccfedbfc3b222cb
https://qiita.com/mshinoda88/items/8bfe0b540b35437296bd
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib