[python] การสร้างค่าสุ่มด้วยการแจกแจงแบบปกติหลายตัวแปร
เขียนเมื่อ 2018/05/25 19:23
แก้ไขล่าสุด 2022/07/19 06:45
ในบทความก่อนหน้านี้ได้อธิบายเรื่องการอธิบายความสัมพันธ์ระหว่างตัวแปรด้วยค่าความแปรปรวนร่วมเกี่ยว (协方差, covariance) และสหสัมพันธ์ (相关系数, correlation) ไป
https://phyblas.hinaboshi.com/20180517
สำหรับในบทความนี้จะพูดถึงเรื่องหนึ่งที่นำมาประยุกต์ใช้ได้ คือใช้สร้างข้อมูลที่มีการแจกแจงแบบปกติหลายตัวแปร (多元正态分布, multivariate normal distribution)
โดยพื้นฐานแล้ว numpy มีฟังก์ชันสำหรับสร้างข้อมูลสุ่มอยู่มากมาย ส่วนหนึ่งได้เขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/numa15
แต่ในนี้จะขอแนะนำฟังก์ชัน np.random.multivariate_normal() ซึ่งไว้ใช้สร้างการแจกแจงแบบปกติหลายตัวแปร
การจะใช้ได้จำเป็นต้องอาศัยความเข้าใจเรื่องความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์
การแจกแจงแบบปกติตัวแปรเดียว
ก่อนอื่นมาทวนเรื่องการแจกแจงแบบปกติตัวแปรเดียวก่อน
การแจกแจงแบบปกติ (正态分布, normal distribution) หรืออาจเรียกว่า การแจกแจงแบบเกาส์ (高斯分布, Gaussian distribution) เป็นการแจกแจงในรูปแบบที่ใช้บ่อยที่สุด
การแจกแจงแบบปกติเป็นการแจกแจงที่ขึ้นอยู่กับพารามิเตอร์ ๒ ตัวที่ต้องกำหนดคือ
- μ คือ จุดกึ่งกลาง
- σ คือ ส่วนเบี่ยงเบนมาตรฐาน
โดยความหนาแน่นของการแจกแจงจะเป็นไปตามสมการนี้
..(1)
หากเขียนเป็นฟังก์ชันในไพธอนแล้ววาดกราฟจะเป็นแบบนี้
กราฟเป็นรูประฆังคว่ำ ค่าจะมากสุดที่จุด μ และค่อยๆลดลงเมื่อยิ่งห่างออกไป อัตราการลดลงจะเร็วแค่ไหนขึ้นอยู่กับ σ
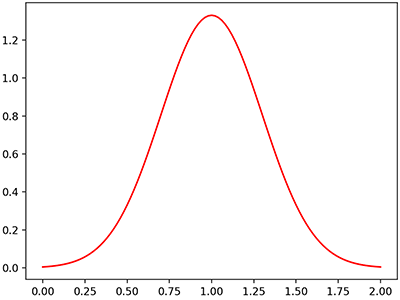
หากสร้างค่าสุ่มให้แจกแจงแบบปกติโดยกำหนดค่า μ และ σ ที่ค่าหนึ่ง เมื่อนำมาหาค่าเฉลี่ยก็จะได้ประมาณ μ ส่วนเบี่ยงเบนมาตรฐานก็จะได้ประมาณ σ
ในไพธอนสามารถสร้างการแจกแจงแบบปกติได้ด้วยฟังก์ชัน np.random.normal พารามิเตอร์คือ (μ, σ, จำนวนที่ต้องการสุ่ม)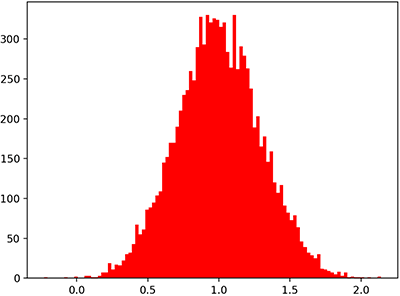
หากลองสร้างสองตัวแปรที่แจกแจงแบบปกติพร้อมกันแล้วหาความแปรปรวนร่วมเกี่ยวดู
จะได้ว่าค่าในแนวทแยงก็คือค่า σ กำลังสอง ส่วนขวาบนซ้ายล่างเข้าใกล้ 0 นั่นเพราะทั้ง ๒ ตัวแปรถูกสุ่มอย่างอิสระไม่ได้เกี่ยวข้องต่อกันเลย
แต่ว่าในธรรมชาติโดยทั่วไปแล้ว ตัวแปรสองตัวที่มีการแจกแจงแบบปกติอาจมีความเกี่ยวพันกัน เช่นพอตัวนึงมากอีกตัวนึงก็มีแนวโน้มมากหรือน้อยตาม
กรณีแบบนี้จะต้องสร้างตัวแปรทั้งสองพร้อมกันด้วยการแจกแจงแบบปกติหลายตัวแปร
การแจกแจงแบบปกติหลายตัวแปร
หากมีตัวแปร x และ y ที่ต้องการให้แจกแจงแบบปกติโดยมีความเกี่ยวเนื่องกัน อาจเขียนสมการการแจกแจงได้ดังนี้
..(2)
โดย ρxy คือค่าสหสัมพันธ์ของ x และ y
..(3)
จะเห็นว่าเดิมทีที่เป็นแค่ (x-μx)2 ได้ถูกเปลี่ยนมาเป็นก้อนที่ซับซ้อนมากขึ้น มีทั้งส่วนร่วมของ x และ y อยู่ด้วยกัน
สมการอาจเขียนเป็นรูปทั่วไปด้วยเมทริกซ์ได้แบบนี้
..(4)
โดย x ในที่นี้ใช้ตัวหนา หมายถึงเป็นปริมาณเวกเตอร์
Σ คือเมทริกซ์ความแปรปรวนร่วมเกี่ยว โดย |Σ| คือดีเทอร์มิแนนต์ (determinant) ของเมทริกซ์ Σ
กรณีที่มีตัวแปรแค่ x และ y นั้น Σ จะเป็นแบบนี้
..(5)
กรณีที่มีหลายตัวแปรจะได้ว่า
..(6)
ส่วน x-μ ในที่นี้คือเวกเตอร์ที่แสดงถึงระยะห่างจากจุดกึ่งกลางของตัวแปรต่างๆ เมื่อนำมาคูณประกบกันกับเมทริกซ์ความแปรปรวนร่วมเกี่ยวในลักษณะแบบนี้สิ่งที่ได้ก็คือสิ่งที่เรียกว่า ระยะทางมหาลโนพิส (Mahalanobis distance)
..(7)
ชื่อที่ฟังดูยืดยาวจำยากนี้ถูกตั้งตามนักคณิตศาสตร์ชาวอินเดียชื่อ ประศานตะ จันทระ มหาลโนพิส (प्रशान्त चन्द्र महालनोबिस)
เมื่อสมการอยู่ในรูปเมทริกซ์แบบนี้อาจดูแล้วเข้าใจยากหน่อย แต่ในแง่ของการเขียนโปรแกรมคำนวณแล้วเป็นอะไรที่สะดวก เพราะเมทริกซ์นึงคือตัวแปรตัวนึง
ในไพธอนเมทริกซ์จะเขียนอยู่ในรูปตัวแปรชนิดอาเรย์ของ numpy ส่วนการคูณกันของเว็กเตอร์ จะใช้คำสั่ง .dot()
ส่วนการหาดีเทอร์มิแนนท์ก็มีคำสั่ง np.linalg.det() การหาเมทริกซ์ผกผันก็ใช้ np.linalg.inv()
เราอาจเขียนโปรแกรมให้คำนวณตามสมการ (4) ได้ดังนี้
นอกจากนี้ใน scipy ได้เตรียมฟังก์ชันแบบนี้ไว้ คือ scipy.stats.multivariate_normal.pdf ใช้อันนี้ได้เลย
ลองนำมาใช้วาดแผนภาพแสดงการแจกแจงในสองมิติดู โดยแสดงผลดูทั้งแบบสามมิติและแบบคอนทัวร์
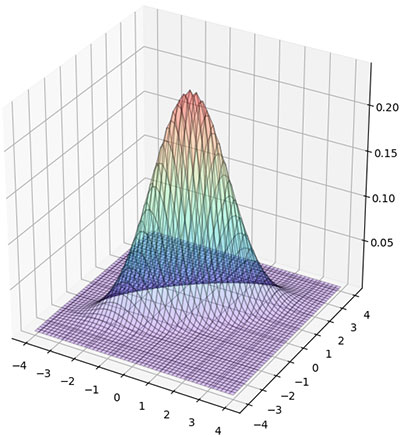
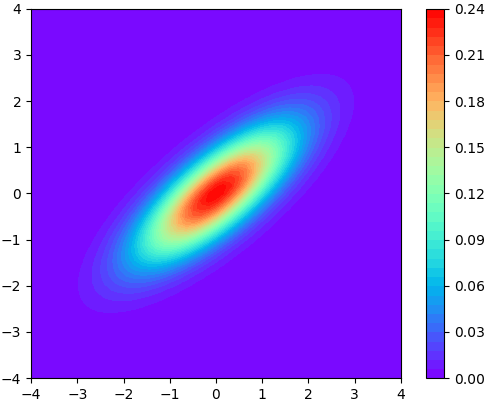
ส่วนการสร้างค่าสุ่มตามการแจกแจงแบบปกติหลายตัวแปรในไพธอนมีฟังก์ชัน np.random.multivariate_normal
วิธีใช้คือ np.random.multivariate_normal(จุดกึ่งกลาง, เมทริกซ์ความแปรปรวนร่วมเกี่ยว, จำนวนที่ต้องการสุ่ม)
ตัวอย่าง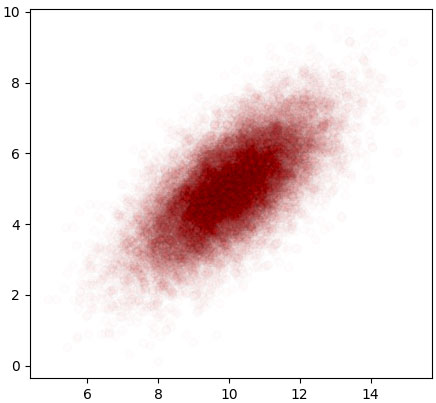
การสร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวด้วยวิธีเคอร์เนล
เพื่อที่จะสร้างข้อมูลสุ่มที่มีการแจกแจงแบบปกติหลายตัวแปร เราจำเป็นต้องมีเมทริกซ์ความแปรปรวนร่วมเกี่ยว
ปกติถ้าเราสร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวขึ้นมาจากการคำนวณ เช่น มีชุดข้อมูลอยู่แล้วนำมาคำนวณด้วยฟังก์ชัน np.cov แบบนั้นแน่นอนว่าเมทริกซ์ที่ได้สามารถนำมาใช้ได้
แต่ถ้าอยู่ดีๆจะสร้างเมทริกซ์ขึ้นมาแล้วนำมาใช้ละก็แบบนั้นไม่ใช่ว่าจะใช้ได้เสมอไป เพราะเมทริกซ์ความแปรปรวนร่วมเกี่ยว โดยทั่วไปมีข้อกำหนดว่า
- ต้องเป็นเมทริกซ์จตุรัส
- ต้องเป็นเมทริกซ์สมมาตร
- ต้องสามารถหาเมทริกซ์ผกผันได้
วิธีหนึ่งที่มักใช้ในการสร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวให้ได้ตามที่ต้องการคือ สร้างจากเคอร์เนล (kernel) คือการนำสมาชิกของตัวแปรชุดนึงทั้งหมดมาจับคู่กระทำอะไรบางอย่างกันแล้วเขียนให้อยู่ในรูปเมทริกซ์
..(8)
โดยในที่นี้ k คือฟังก์ชันที่นำตัวแปร ๒ ตัวมาใช้คำนวณ มักเรียกกันว่าเคอร์เนล
เมทริกซ์ที่ได้จากการจับคู่ทำอะไรกันในลักษณะนี้มีชื่อเรียกว่า เมทริกซ์กรัม (格拉姆矩阵, Gramian matrix) เมทริกซ์ความแปรปรวนร่วมเกี่ยวนั้นโดยทั่วไปถือว่าเป็นเมทริกซ์กรัมชนิดหนึ่ง
ฟังก์ชันที่มักใช้เป็นเคอร์เนลนั้นมีอยู่หลากหลายรูปแบบ
เช่นแบบที่ง่ายที่สุดคือ มีค่าค่าหนึ่งเฉพาะเมื่อ x และ y เท่ากัน คือ
..(9)
โดยในที่นี้ a คือค่าส่วนเบี่ยงเบนมาตรฐาน
เขียนในไพธอนได้แบบนี้
เมื่อใช้คำนวณก็จะได้ผลที่เป็นแบบที่เรียบง่ายที่สุดก็คือเมทริกซ์แนวทแยง คือมีค่าแต่ในแนวทแยงนอกนั้น 0 ซึ่งจะหมายถึงว่าตัวแปรทั้งหมดมีการแจกแจงในตัวเองที่เป็นอิสระจากตัวแปรอื่นใด
..(10)
หากนำเมทริกซ์แบบนั้นมาใช้สร้างข้อมูลที่เป็นอนุกรมเวลาก็จะได้ข้อมูลที่เป็นการสุ่มแยกกันโดยสมบูรณ์ ค่าของจุดก่อนและหลังไม่มีผลต่อจุดนั้นๆเลย
เช่น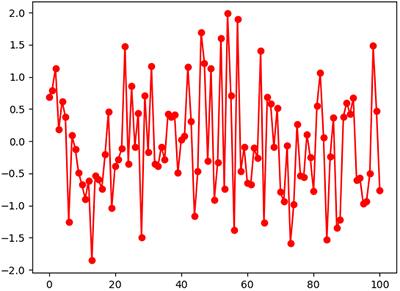
เคอร์เนลกำลังสองเอ็กซ์โพเนนเชียล
ในการสร้างข้อมูลที่เป็นอนุกรมเวลาที่ค่าในจุดนึงสัมพันธ์กับจุดก่อนและหลัง เคอร์เนลแบบหนึ่งที่นิยมใช้กันมากก็คือกำลังสองเอ็กซ์โพเนนเชียล (squared-exponential)
..(11)
..(12)
โดย a เป็นตัวกำหนดขนาดการแจกแจง (ส่วนเบี่ยงเบนมาตรฐาน) ส่วน s กำหนดขนาดระยะที่ความเกี่ยวพันจะส่งผลไปถึง
สามารถสร้างฟังก์ชันเคอร์เนลตามสมการได้ดังนี้
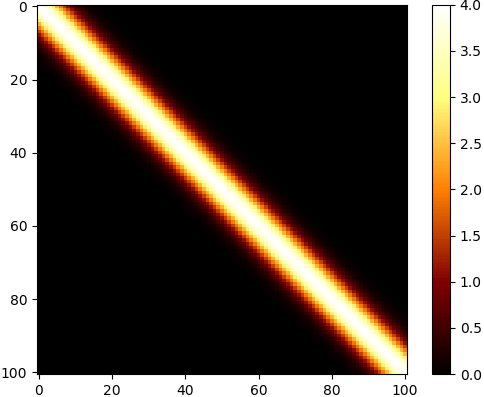
แล้วลองนำเคอร์เนลมาใช้สร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวสำหรับข้อมูลอนุกรมเวลา
จะได้ค่าสูงสุดที่แนวทแยง โดยมีค่าเป็น a ยกกำลังสอง และค่อยๆลดลงเมื่อห่างออกไป
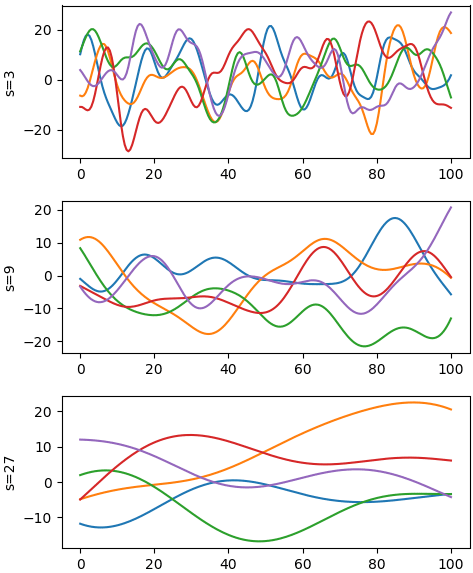
จากนั้นก็นำมาใช้ สุ่มสร้างอนุกรมเวลา โดยลองเทียบค่า s ต่างกัน สร้างดูสักแบบละ ๕ เส้น
จะเห็นว่าแต่ละเส้นที่ได้มีลักษณะที่มีการเปลี่ยนแปลงไปทีละเล็กน้อย ค่าในจุดนึงจะขึ้นอยู่กับจุดก่อนหลัง ไม่ได้โดดไปไกลนัก และยิ่งค่า s มากขึ้น ความเปลี่ยนแปลงก็จะยิ่งน้อย
นอกจากนี้เรายังอาจเอาเคอร์เนลมารวมกันได้ เช่น
..(13)
แบบนี้จะได้การเปลี่ยนแปลงที่โดยรวมแล้วมีลักษณะค่อยเป็นค่อยไปตามเวลา แต่ก็มีการเปลี่ยนแปลงขึ้นลงจากความไม่แน่นอนภายในตัว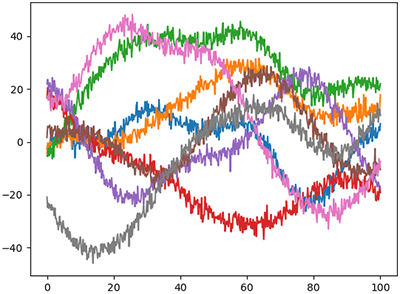
การเปลี่ยนแปลงแบบเป็นคาบ
บางครั้งเราอาจต้องการสุ่มสร้างค่าบางอย่างที่มีการเปลี่ยนแปลงแบบเป็นคาบ (periodic) คือเมื่อถึงจุดนึงจะกลับมามีค่าเท่าเดิม กรณีแบบนี้นิยมใช้เคอร์เนลแบบไซน์กำลังสองเอ็กซ์โพเนนเชียล (exp-sine-squared kernel)
..(14)
ในที่นี้ τ คือคาบ คือเป็นตัวกำหนดว่าไปไกลแค่ไหนจะกลับมาวนซ้ำ
ส่วน s คือตัวกำหนดว่าจะมีความเปลี่ยนแปลงขึ้นลงบ่อยแค่ไหนในคาบ ยิ่งน้อยยิ่งขึ้นลงมาก
ลองดูค่าในเมทริกซ์ความแปรปรวนร่วมเกี่ยวที่ได้จากการคำนวณ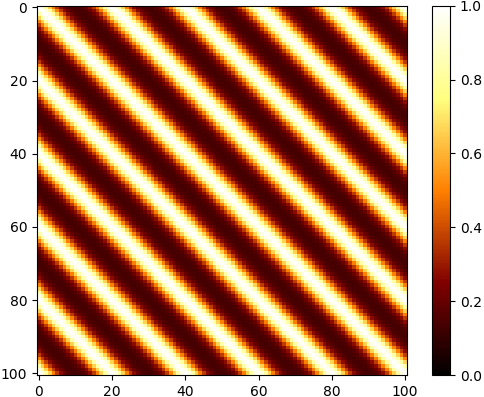
ลองนำมาใช้แล้ววาดกราฟดู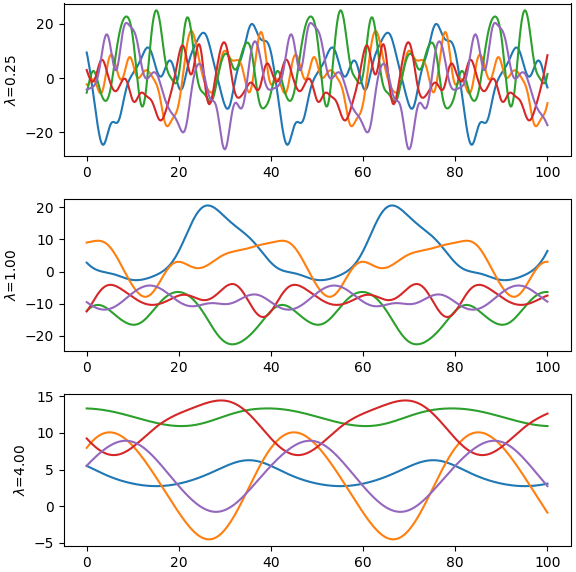
การเปลี่ยนแปลงแบบเกือบเป็นคาบ
บางครั้งเราอาจต้องการได้ค่าที่มีการเปลี่ยนแปลงเป็นคาบ แต่ไม่ได้เหมือนเดิมตลอดทุกคาบ แต่ในแต่ละคาบมีการเปลี่ยนแปลงไปทีละน้อย ลักษณะแบบนั้นเรียกว่า quasi-periodic ซึ่งอาจแปลเป็นไทยว่า "เกือบเป็นคาบ"
เราสามารถทำเคอร์เนลในลักษณะนี้ได้โดยเอาเคอร์เนลแบบไซน์กำลังสองเอ็กซ์โพเนนเชียลมาคูณกับกำลังสองเอ็กซ์โพเนนเชียล กลายเป็นแบบนี้
..(15)
ตัวอย่าง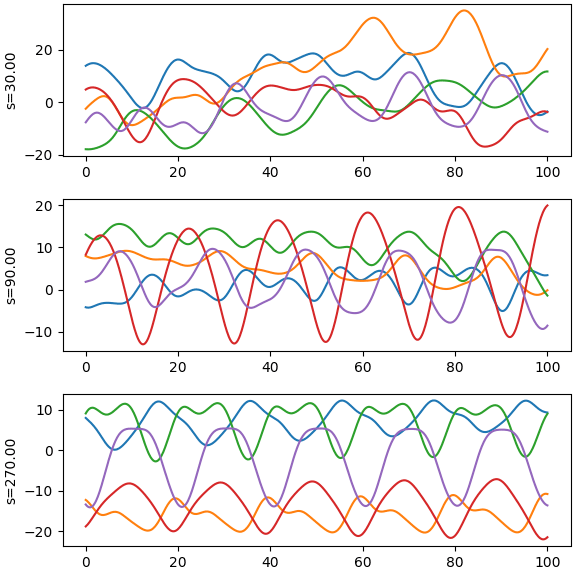
ค่าจะกลับมาเหมือนเดิมทุก 20 แต่ไม่ได้เหมือนกันเป๊ะ แต่ยิ่ง s มาก ความแตกต่างของแต่ละรอบก็จะยิ่งน้อยลง
นี่เป็นแค่คัวอย่างส่วนหนึ่งเท่านั้น นอกจากนี้ยังมีรูปแบบการใช้อยู่อีกมากมายสามารถไปลองศึกษาเพิ่มเติมกันได้
สรุปเนื้อหาทั้งหมดนี้น่าจะทำให้เข้าใจวิธีการสร้างชุดข้อมูลจากการสุ่มค่าด้วยฟังก์ชัน np.random.multivariate_normal ตามที่ต้องการกันได้ไม่มากก็น้อยแล้ว
https://phyblas.hinaboshi.com/20180517
สำหรับในบทความนี้จะพูดถึงเรื่องหนึ่งที่นำมาประยุกต์ใช้ได้ คือใช้สร้างข้อมูลที่มีการแจกแจงแบบปกติหลายตัวแปร (多元正态分布, multivariate normal distribution)
โดยพื้นฐานแล้ว numpy มีฟังก์ชันสำหรับสร้างข้อมูลสุ่มอยู่มากมาย ส่วนหนึ่งได้เขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/numa15
แต่ในนี้จะขอแนะนำฟังก์ชัน np.random.multivariate_normal() ซึ่งไว้ใช้สร้างการแจกแจงแบบปกติหลายตัวแปร
การจะใช้ได้จำเป็นต้องอาศัยความเข้าใจเรื่องความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์
การแจกแจงแบบปกติตัวแปรเดียว
ก่อนอื่นมาทวนเรื่องการแจกแจงแบบปกติตัวแปรเดียวก่อน
การแจกแจงแบบปกติ (正态分布, normal distribution) หรืออาจเรียกว่า การแจกแจงแบบเกาส์ (高斯分布, Gaussian distribution) เป็นการแจกแจงในรูปแบบที่ใช้บ่อยที่สุด
การแจกแจงแบบปกติเป็นการแจกแจงที่ขึ้นอยู่กับพารามิเตอร์ ๒ ตัวที่ต้องกำหนดคือ
- μ คือ จุดกึ่งกลาง
- σ คือ ส่วนเบี่ยงเบนมาตรฐาน
โดยความหนาแน่นของการแจกแจงจะเป็นไปตามสมการนี้
..(1)
หากเขียนเป็นฟังก์ชันในไพธอนแล้ววาดกราฟจะเป็นแบบนี้
import numpy as np
import matplotlib.pyplot as plt
def pakati(x,mu,sigma):
return np.exp(-(x-mu)**2/(2*sigma**2))/np.sqrt(2*np.pi)/sigma
x = np.linspace(0,2,101)
y = pakati(x,1,0.3)
plt.plot(x,y,'r')
plt.show()กราฟเป็นรูประฆังคว่ำ ค่าจะมากสุดที่จุด μ และค่อยๆลดลงเมื่อยิ่งห่างออกไป อัตราการลดลงจะเร็วแค่ไหนขึ้นอยู่กับ σ

หากสร้างค่าสุ่มให้แจกแจงแบบปกติโดยกำหนดค่า μ และ σ ที่ค่าหนึ่ง เมื่อนำมาหาค่าเฉลี่ยก็จะได้ประมาณ μ ส่วนเบี่ยงเบนมาตรฐานก็จะได้ประมาณ σ
ในไพธอนสามารถสร้างการแจกแจงแบบปกติได้ด้วยฟังก์ชัน np.random.normal พารามิเตอร์คือ (μ, σ, จำนวนที่ต้องการสุ่ม)
s = np.random.normal(1,0.3,10000)
plt.hist(s,100,color='r')
plt.show()
print(s.mean()) # ได้ 0.9987304195735669
print(s.std()) # ได้ 0.2962901261818392
หากลองสร้างสองตัวแปรที่แจกแจงแบบปกติพร้อมกันแล้วหาความแปรปรวนร่วมเกี่ยวดู
x = np.random.normal(12,2,100000)
y = np.random.normal(27,1,100000)
plt.axes(aspect=1,xlim=[x.min(),x.max()],ylim=[y.min(),y.max()])
plt.scatter(x,y,c='r',edgecolors='k',alpha=0.01)
plt.show()
print(np.cov(x,y))จะได้ว่าค่าในแนวทแยงก็คือค่า σ กำลังสอง ส่วนขวาบนซ้ายล่างเข้าใกล้ 0 นั่นเพราะทั้ง ๒ ตัวแปรถูกสุ่มอย่างอิสระไม่ได้เกี่ยวข้องต่อกันเลย
แต่ว่าในธรรมชาติโดยทั่วไปแล้ว ตัวแปรสองตัวที่มีการแจกแจงแบบปกติอาจมีความเกี่ยวพันกัน เช่นพอตัวนึงมากอีกตัวนึงก็มีแนวโน้มมากหรือน้อยตาม
กรณีแบบนี้จะต้องสร้างตัวแปรทั้งสองพร้อมกันด้วยการแจกแจงแบบปกติหลายตัวแปร
การแจกแจงแบบปกติหลายตัวแปร
หากมีตัวแปร x และ y ที่ต้องการให้แจกแจงแบบปกติโดยมีความเกี่ยวเนื่องกัน อาจเขียนสมการการแจกแจงได้ดังนี้
..(2)
โดย ρxy คือค่าสหสัมพันธ์ของ x และ y
..(3)
จะเห็นว่าเดิมทีที่เป็นแค่ (x-μx)2 ได้ถูกเปลี่ยนมาเป็นก้อนที่ซับซ้อนมากขึ้น มีทั้งส่วนร่วมของ x และ y อยู่ด้วยกัน
สมการอาจเขียนเป็นรูปทั่วไปด้วยเมทริกซ์ได้แบบนี้
..(4)
โดย x ในที่นี้ใช้ตัวหนา หมายถึงเป็นปริมาณเวกเตอร์
Σ คือเมทริกซ์ความแปรปรวนร่วมเกี่ยว โดย |Σ| คือดีเทอร์มิแนนต์ (determinant) ของเมทริกซ์ Σ
กรณีที่มีตัวแปรแค่ x และ y นั้น Σ จะเป็นแบบนี้
..(5)
กรณีที่มีหลายตัวแปรจะได้ว่า
..(6)
ส่วน x-μ ในที่นี้คือเวกเตอร์ที่แสดงถึงระยะห่างจากจุดกึ่งกลางของตัวแปรต่างๆ เมื่อนำมาคูณประกบกันกับเมทริกซ์ความแปรปรวนร่วมเกี่ยวในลักษณะแบบนี้สิ่งที่ได้ก็คือสิ่งที่เรียกว่า ระยะทางมหาลโนพิส (Mahalanobis distance)
..(7)
ชื่อที่ฟังดูยืดยาวจำยากนี้ถูกตั้งตามนักคณิตศาสตร์ชาวอินเดียชื่อ ประศานตะ จันทระ มหาลโนพิส (प्रशान्त चन्द्र महालनोबिस)
เมื่อสมการอยู่ในรูปเมทริกซ์แบบนี้อาจดูแล้วเข้าใจยากหน่อย แต่ในแง่ของการเขียนโปรแกรมคำนวณแล้วเป็นอะไรที่สะดวก เพราะเมทริกซ์นึงคือตัวแปรตัวนึง
ในไพธอนเมทริกซ์จะเขียนอยู่ในรูปตัวแปรชนิดอาเรย์ของ numpy ส่วนการคูณกันของเว็กเตอร์ จะใช้คำสั่ง .dot()
ส่วนการหาดีเทอร์มิแนนท์ก็มีคำสั่ง np.linalg.det() การหาเมทริกซ์ผกผันก็ใช้ np.linalg.inv()
เราอาจเขียนโปรแกรมให้คำนวณตามสมการ (4) ได้ดังนี้
def pakati(X,mu,cov):
d = X-mu
k = len(d)
det = np.linalg.det(cov)
inv = np.linalg.inv(cov)
m = d.T.dot(inv).dot(d) # กำลังสองของระยะห่าง mahalanobis
return np.exp(-m/2)/np.sqrt((2*np.pi)**k*det)นอกจากนี้ใน scipy ได้เตรียมฟังก์ชันแบบนี้ไว้ คือ scipy.stats.multivariate_normal.pdf ใช้อันนี้ได้เลย
ลองนำมาใช้วาดแผนภาพแสดงการแจกแจงในสองมิติดู โดยแสดงผลดูทั้งแบบสามมิติและแบบคอนทัวร์
from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal
mu = np.array([0,0])
cov = np.array([[1.2,0.8],[0.8,0.9]])
mx,my = np.meshgrid(np.linspace(-4,4,51),np.linspace(-4,4,51))
mX = np.stack([mx,my],2)
mz = multivariate_normal.pdf(mX,mu,cov)
ax = plt.figure(figsize=[6,6]).add_axes([0,0,1,1],projection='3d')
ax.plot_surface(mx,my,mz,rstride=1,cstride=1,alpha=0.2,edgecolor='k',cmap='rainbow')
plt.figure()
plt.axes(aspect=1)
plt.contourf(mx,my,mz,40,cmap='rainbow')
plt.colorbar()
plt.show()

ส่วนการสร้างค่าสุ่มตามการแจกแจงแบบปกติหลายตัวแปรในไพธอนมีฟังก์ชัน np.random.multivariate_normal
วิธีใช้คือ np.random.multivariate_normal(จุดกึ่งกลาง, เมทริกซ์ความแปรปรวนร่วมเกี่ยว, จำนวนที่ต้องการสุ่ม)
ตัวอย่าง
mu = np.array([10,5])
cov = np.array([[1.8,1.1],[1.1,1.5]])
X = np.random.multivariate_normal(mu,cov,20000)
plt.figure()
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],edgecolors='k',color='r',alpha=0.01)
plt.show()
การสร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวด้วยวิธีเคอร์เนล
เพื่อที่จะสร้างข้อมูลสุ่มที่มีการแจกแจงแบบปกติหลายตัวแปร เราจำเป็นต้องมีเมทริกซ์ความแปรปรวนร่วมเกี่ยว
ปกติถ้าเราสร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวขึ้นมาจากการคำนวณ เช่น มีชุดข้อมูลอยู่แล้วนำมาคำนวณด้วยฟังก์ชัน np.cov แบบนั้นแน่นอนว่าเมทริกซ์ที่ได้สามารถนำมาใช้ได้
แต่ถ้าอยู่ดีๆจะสร้างเมทริกซ์ขึ้นมาแล้วนำมาใช้ละก็แบบนั้นไม่ใช่ว่าจะใช้ได้เสมอไป เพราะเมทริกซ์ความแปรปรวนร่วมเกี่ยว โดยทั่วไปมีข้อกำหนดว่า
- ต้องเป็นเมทริกซ์จตุรัส
- ต้องเป็นเมทริกซ์สมมาตร
- ต้องสามารถหาเมทริกซ์ผกผันได้
วิธีหนึ่งที่มักใช้ในการสร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวให้ได้ตามที่ต้องการคือ สร้างจากเคอร์เนล (kernel) คือการนำสมาชิกของตัวแปรชุดนึงทั้งหมดมาจับคู่กระทำอะไรบางอย่างกันแล้วเขียนให้อยู่ในรูปเมทริกซ์
..(8)
โดยในที่นี้ k คือฟังก์ชันที่นำตัวแปร ๒ ตัวมาใช้คำนวณ มักเรียกกันว่าเคอร์เนล
เมทริกซ์ที่ได้จากการจับคู่ทำอะไรกันในลักษณะนี้มีชื่อเรียกว่า เมทริกซ์กรัม (格拉姆矩阵, Gramian matrix) เมทริกซ์ความแปรปรวนร่วมเกี่ยวนั้นโดยทั่วไปถือว่าเป็นเมทริกซ์กรัมชนิดหนึ่ง
ฟังก์ชันที่มักใช้เป็นเคอร์เนลนั้นมีอยู่หลากหลายรูปแบบ
เช่นแบบที่ง่ายที่สุดคือ มีค่าค่าหนึ่งเฉพาะเมื่อ x และ y เท่ากัน คือ
..(9)
โดยในที่นี้ a คือค่าส่วนเบี่ยงเบนมาตรฐาน
เขียนในไพธอนได้แบบนี้
def kernel(x,a):
x1,x2 = np.meshgrid(x,x)
return a**2*(x1==x2)เมื่อใช้คำนวณก็จะได้ผลที่เป็นแบบที่เรียบง่ายที่สุดก็คือเมทริกซ์แนวทแยง คือมีค่าแต่ในแนวทแยงนอกนั้น 0 ซึ่งจะหมายถึงว่าตัวแปรทั้งหมดมีการแจกแจงในตัวเองที่เป็นอิสระจากตัวแปรอื่นใด
..(10)
หากนำเมทริกซ์แบบนั้นมาใช้สร้างข้อมูลที่เป็นอนุกรมเวลาก็จะได้ข้อมูลที่เป็นการสุ่มแยกกันโดยสมบูรณ์ ค่าของจุดก่อนและหลังไม่มีผลต่อจุดนั้นๆเลย
เช่น
def kernel(x,a):
x1,x2 = np.meshgrid(x,x)
return a**2*(x1==x2)
x = np.linspace(0,100,101)
mu = np.zeros(101)
cov = kernel(x,1)
y = np.random.multivariate_normal(mu,cov)
plt.plot(x,y,'r-o')
plt.show()
เคอร์เนลกำลังสองเอ็กซ์โพเนนเชียล
ในการสร้างข้อมูลที่เป็นอนุกรมเวลาที่ค่าในจุดนึงสัมพันธ์กับจุดก่อนและหลัง เคอร์เนลแบบหนึ่งที่นิยมใช้กันมากก็คือกำลังสองเอ็กซ์โพเนนเชียล (squared-exponential)
..(11)
..(12)
โดย a เป็นตัวกำหนดขนาดการแจกแจง (ส่วนเบี่ยงเบนมาตรฐาน) ส่วน s กำหนดขนาดระยะที่ความเกี่ยวพันจะส่งผลไปถึง
สามารถสร้างฟังก์ชันเคอร์เนลตามสมการได้ดังนี้
def kernel(x,a,s):
x1,x2 = np.meshgrid(x,x)
return a**2*np.exp(-0.5*((x1-x2)/s)**2)แล้วลองนำเคอร์เนลมาใช้สร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวสำหรับข้อมูลอนุกรมเวลา
x = np.linspace(0,100,101)
cov = kernel(x,2,5)
plt.imshow(cov,cmap='afmhot')
plt.colorbar()
plt.show()จะได้ค่าสูงสุดที่แนวทแยง โดยมีค่าเป็น a ยกกำลังสอง และค่อยๆลดลงเมื่อห่างออกไป

จากนั้นก็นำมาใช้ สุ่มสร้างอนุกรมเวลา โดยลองเทียบค่า s ต่างกัน สร้างดูสักแบบละ ๕ เส้น
plt.figure(figsize=[5,6])
x = np.linspace(0,100,201)
mu = np.zeros(201)
for i in range(1,4):
s = 3**i
cov = kernel(x,10,s)
y = np.random.multivariate_normal(mu,cov,5)
plt.subplot(3,1,i)
plt.plot(x,y.T)
plt.ylabel('s=%d'%s)
plt.tight_layout()
plt.show()จะเห็นว่าแต่ละเส้นที่ได้มีลักษณะที่มีการเปลี่ยนแปลงไปทีละเล็กน้อย ค่าในจุดนึงจะขึ้นอยู่กับจุดก่อนหลัง ไม่ได้โดดไปไกลนัก และยิ่งค่า s มากขึ้น ความเปลี่ยนแปลงก็จะยิ่งน้อย

นอกจากนี้เรายังอาจเอาเคอร์เนลมารวมกันได้ เช่น
..(13)
def kernel(x,a1,s,a2):
x1,x2 = np.meshgrid(x,x)
return a1**2*np.exp(-0.5*((x1-x2)/s)**2) + a2**2*(x1==x2)แบบนี้จะได้การเปลี่ยนแปลงที่โดยรวมแล้วมีลักษณะค่อยเป็นค่อยไปตามเวลา แต่ก็มีการเปลี่ยนแปลงขึ้นลงจากความไม่แน่นอนภายในตัว
x = np.linspace(0,100,501)
mu = np.zeros(501)
cov = kernel(x,20,15,2)
y = np.random.multivariate_normal(mu,cov,8)
plt.plot(x,y.T)
plt.show()
การเปลี่ยนแปลงแบบเป็นคาบ
บางครั้งเราอาจต้องการสุ่มสร้างค่าบางอย่างที่มีการเปลี่ยนแปลงแบบเป็นคาบ (periodic) คือเมื่อถึงจุดนึงจะกลับมามีค่าเท่าเดิม กรณีแบบนี้นิยมใช้เคอร์เนลแบบไซน์กำลังสองเอ็กซ์โพเนนเชียล (exp-sine-squared kernel)
..(14)
def kernel(x,a,tau,l):
x1,x2 = np.meshgrid(x,x)
return a**2*np.exp(-2*(np.sin((x1-x2)*np.pi/tau)/l)**2)ในที่นี้ τ คือคาบ คือเป็นตัวกำหนดว่าไปไกลแค่ไหนจะกลับมาวนซ้ำ
ส่วน s คือตัวกำหนดว่าจะมีความเปลี่ยนแปลงขึ้นลงบ่อยแค่ไหนในคาบ ยิ่งน้อยยิ่งขึ้นลงมาก
ลองดูค่าในเมทริกซ์ความแปรปรวนร่วมเกี่ยวที่ได้จากการคำนวณ
x = np.linspace(0,100,101)
cov = kernel(x,1,20,1)
plt.imshow(cov,cmap='afmhot',vmin=0,vmax=1)
plt.colorbar()
plt.show()
ลองนำมาใช้แล้ววาดกราฟดู
x = np.linspace(0,100,501)
mu = np.zeros(501)
plt.figure(figsize=[6,6])
for i in range(1,4):
l = 4**(i-2)
cov = kernel(x,10,40,l)
y = np.random.multivariate_normal(mu,cov,5)
plt.subplot(3,1,i)
plt.plot(x,y.T)
plt.ylabel(r'$\lambda$=%.2f'%l)
plt.tight_layout()
plt.show()
การเปลี่ยนแปลงแบบเกือบเป็นคาบ
บางครั้งเราอาจต้องการได้ค่าที่มีการเปลี่ยนแปลงเป็นคาบ แต่ไม่ได้เหมือนเดิมตลอดทุกคาบ แต่ในแต่ละคาบมีการเปลี่ยนแปลงไปทีละน้อย ลักษณะแบบนั้นเรียกว่า quasi-periodic ซึ่งอาจแปลเป็นไทยว่า "เกือบเป็นคาบ"
เราสามารถทำเคอร์เนลในลักษณะนี้ได้โดยเอาเคอร์เนลแบบไซน์กำลังสองเอ็กซ์โพเนนเชียลมาคูณกับกำลังสองเอ็กซ์โพเนนเชียล กลายเป็นแบบนี้
..(15)
ตัวอย่าง
def kernel(x,a,tau,l,s):
x1,x2 = np.meshgrid(x,x)
dx = x1-x2
return a**2*np.exp(-2*(np.sin(dx*np.pi/tau)/l)**2-0.5*(dx/s)**2)
x = np.linspace(0,100,501)
mu = np.zeros(501)
plt.figure(figsize=[6,6])
for i in range(1,4):
s = 3**i*10
cov = kernel(x,10,20,2,s)
y = np.random.multivariate_normal(mu,cov,5)
plt.subplot(3,1,i)
plt.plot(x,y.T)
plt.ylabel(r's=%.2f'%s)
plt.tight_layout()
plt.show()
ค่าจะกลับมาเหมือนเดิมทุก 20 แต่ไม่ได้เหมือนกันเป๊ะ แต่ยิ่ง s มาก ความแตกต่างของแต่ละรอบก็จะยิ่งน้อยลง
นี่เป็นแค่คัวอย่างส่วนหนึ่งเท่านั้น นอกจากนี้ยังมีรูปแบบการใช้อยู่อีกมากมายสามารถไปลองศึกษาเพิ่มเติมกันได้
สรุปเนื้อหาทั้งหมดนี้น่าจะทำให้เข้าใจวิธีการสร้างชุดข้อมูลจากการสุ่มค่าด้วยฟังก์ชัน np.random.multivariate_normal ตามที่ต้องการกันได้ไม่มากก็น้อยแล้ว
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy-- คณิตศาสตร์
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib