[python] ทำความเข้าใจคอนโวลูชัน
เขียนเมื่อ 2018/06/09 08:52
แก้ไขล่าสุด 2021/09/28 16:42
ใครที่ศึกษาเรื่องการเรียนรู้ของเครื่อง โดยเฉพาะโครงข่ายประสาทเทียมคงจะรู้จักสิ่งที่เรียกว่าโครงข่ายประสาทแบบคอนโวลูชัน (convolutional neural network) ซึ่งถูกใช้อย่างกว้างขวางในการวิเคราะห์ข้อมูลรูปภาพหรืออนุกรมเวลา
ในบทความนี้จะอธิบายให้เห็นภาพว่าคอนโวลูชันที่ว่านี้คืออะไร โดยใช้ภาพประกอบที่เขียนจากไพธอนแสดงให้เห็นภาพชัด
ความหมายของคอนโวลูชัน
คอนโวลูชัน (convolution) หากเปิดพจนานุกรมภาษาอังกฤษก็จะพบว่ามีความหมายโดยทั่วไปว่า การบิดงอหมุนวน หรืออาจหมายถึงรอยหยักของสมองก็ได้ แต่ในทางคณิตศาสตร์แล้วมีความหมายเฉพาะอีกอย่าง
ที่จริงคอนโวลูชันมีชื่อแปลไทยว่า "สังวัตนาการ" ด้วย อย่างไรก็ตามนี่เป็นคำแปลที่แปลแล้วยากขึ้นกว่าเดิมและไม่ได้ช่วยให้เข้าใจความหมาย จึงไม่เป็นที่นิยม ในที่นี้ก็จะขอใช้ทับศัพท์
ความหมายของคอนโวลูชันนั้นหากดูแปลจีนหรือแปลญี่ปุ่น น่าจะช่วยให้เข้าใจเห็นภาพได้ชัด
ในภาษาญี่ปุ่นแปลคำนี้ว่า 畳み込み tatamikomi หมายถึงการ "พับทบแล้วอัดแน่น"
ส่วนในภาษาจีนคือ 卷积(卷積) juǎnjī หมายถึง "ม้วนแล้วกองทับถม"
ซึ่งเป็นการแปลที่อธิบายความหมายของคอนโวลูชันได้เป็นอย่างดี ทำให้แค่เห็นก็พอนึกตามได้คร่าวๆว่ามันคือการทำอะไร
อาจสรุปสั้นๆว่าเป็นการ "ม้วนทบ"
ทีนี้การม้วนทบที่ว่านี่มันคืออย่างไรกัน แค่บอกว่าม้วนทบก็คงนึกภาพไม่ออกอยู่ดีว่าการม้วนทบในทางคณิตศาสตร์นั้นมันม้วนทบยังไง
แต่ถ้าอยู่ดีๆอธิบายนิยามทางคณิตศาสตร์เลย คนทั่วไปก็เข้าใจยาก ดังนั้นขอเริ่มอธิบายด้วยภาพ
นี่คือภาพอธิบายการทำงานของคอนโวลูชัน
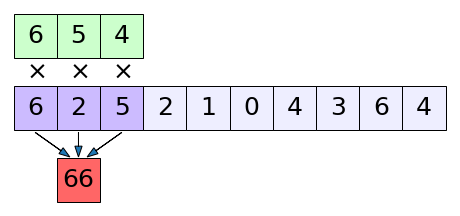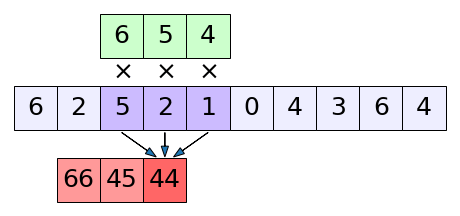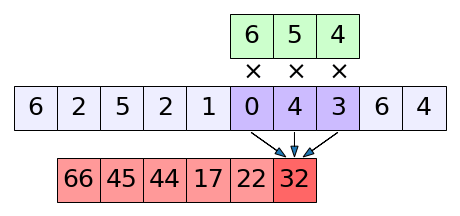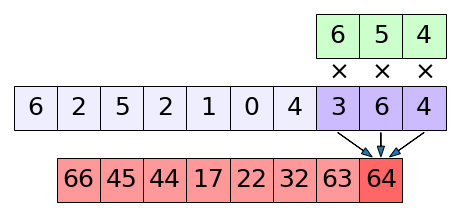
ตัวสีเขียวด้านบนที่วิ่งไปเรื่อยๆนี้เรียกว่าตัวกรอง (filter) แต่บางครั้งก็ถูกเรียกว่าเคอร์เนล (kernel) ส่วนสีม่วงตรงกลางคือข้อมูลป้อนเข้า
ตัวกรองจะคูณกับข้อมูลป้อนเข้าทีละส่วน แล้วเอาผลคูณมาบวกกัน ได้เป็นผลลัพธ์ด้านล่างสีแดง เสร็จแล้วก็เลื่อนตำแหน่งไปจับคู่คูณตำแหน่งถัดไปต่อ
เหมือนเรากำลังเอาตัวกรองมากลิ้งไปบนข้อมูลป้อนเข้า เพื่อจะทบแล้วอัดกันจนได้เป็นผลลัพธ์
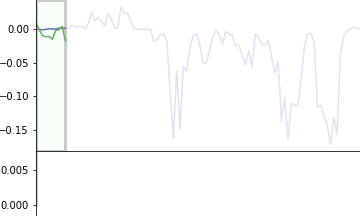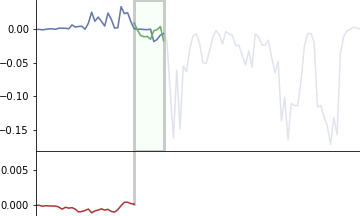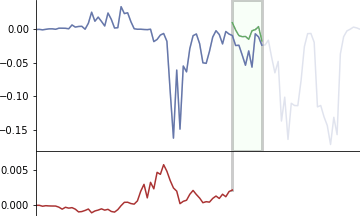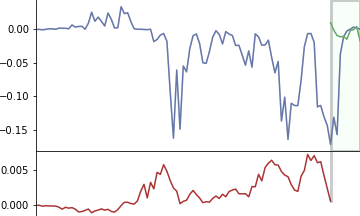
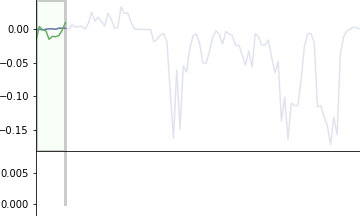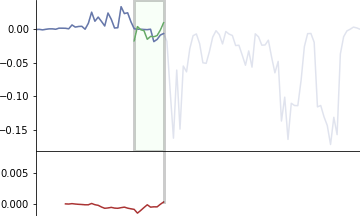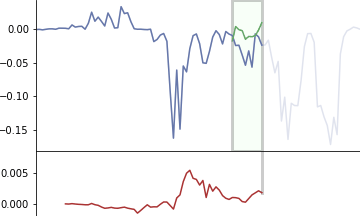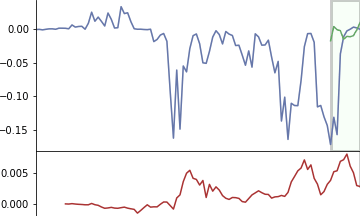
แสดงตัวอย่างอีกภาพ อธิบายด้วยกราฟเส้นวิ่ง เส้นเขียวคือตัวกรองวิ่งไล่คำนวณคูณกับแต่ละส่วนไปเรื่อยๆ แล้วนำผลคูณทั้งหมดทุกช่องมาบวกกัน จนได้ผลออกมาเป็นกราฟข้างล่าง
อย่างไรก็ตาม สิ่งที่เรียกว่าคอนโวลูชันนั้นโดยนิยามดั้งเดิมแล้วจริงๆตัวกรองจะต้องนำมาพลิกกลับด้าน เอาส่วนท้ายไว้หน้า ผลที่ได้ก็จะต่างกัน
คือภาพจะเป็นแบบนี้แทน
ซึ่งอาจเขียนเป็นสูตรคณิตศาสตร์ได้แบบนี้
..(1)
โดย x คืออาเรย์ค่าที่ป้อนเข้า ส่วน k คือตัวกรอง
กรณีภาพแรกคือแบบไม่กลับด้านนั้นมักจะเรียกว่าสหสัมพันธ์ไขว้ (cross-correlation) คือ
..(2)
สหสัมพันธ์ไขว้ในที่นี้เป็นคนละเรื่องกับสหสัมพันธ์ (correlation) ที่เขียนถึงไปใน https://phyblas.hinaboshi.com/20180517
ในที่นี้สัญลักษณ์ ∗ แทนตัวดำเนินการคอนโวลูชัน และ ⋆ แทนสหสัมพันธ์ไขว้
และถ้าหากเป็นกรณีที่ x และ k เป็นฟังก์ชันที่มีค่าต่อเนื่อง แทนที่จะเป็นแค่ข้อมูลเป็นจุดๆ จะเขียนในรูปปริพันธ์แบบนี้
..(3)
คอนโวลูชันในโครงข่ายประสาทเทียมแบบคอนโวลูชันก็ไม่มีการกลับด้านตัวกรอง ดังนั้นจริงๆแล้วในทางเทคนิคมันคือสหสัมพันธ์ไขว้ แต่ถึงอย่างนั้นเขาก็ใช้คำว่าคอนโวลูชันกัน
ดังนั้นในที่นี้ก็จะใช้คำว่าคอนโวลูชันในความหมายนี้ด้วย ตัวกรองจะกลับด้านหรือไม่นั้นไม่ได้เป็นเรื่องที่ต้องคำนึงถึงเมื่อนำมาใช้ในบางเรื่องเช่นในโครงข่ายประสาทเทียม
ลองสร้างฟังก์ชันสำหรับทำคอนโวลูชันขึ้นในไพธอนได้ดังนี้ ตามสมการ (2)
ตัวอย่างการใช้
เพิ่มขอบ (padding)
โดยปกติแล้วเมื่อทำการคอนโวลูชัน ผลที่ได้ออกมาจะเป็นอาเรย์ที่มีขนาดเล็กลง โดยที่
เพราะฉะนั้นเมื่อใช้ตัวกรองขนาด 3 ก็จะทำให้อาเรย์ที่ได้เล็กลงไป 2
แต่ว่าบ่อยครั้งที่เราอาจไม่ต้องการให้ขนาดของผลที่ได้มีการเปลี่ยนแปลง กรณีแบบนี้โดยทั่วไปจะทำได้โดยการเพิ่มขอบลงไปก่อนที่จะทำการคอนโวลูชัน
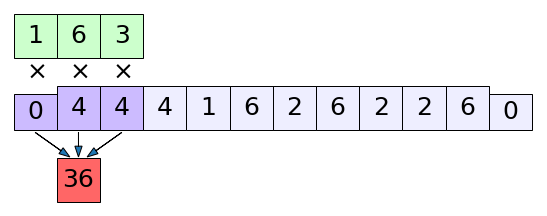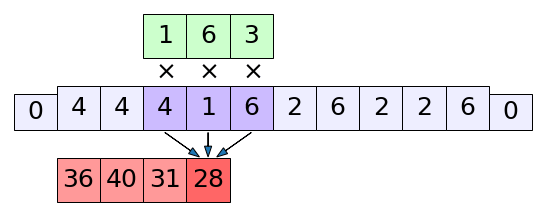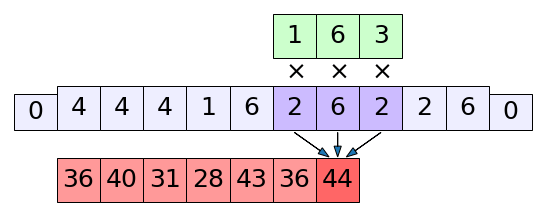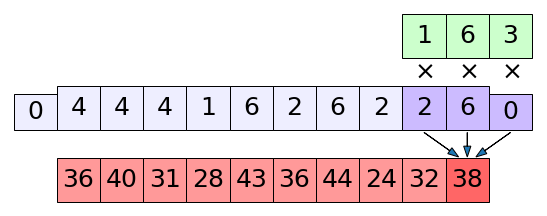
ดูรูปนี้จะเข้าใจง่ายขึ้น มีส่วนขอบที่เพิ่มเข้ามาทางซ้ายขวา โดยจะมีค่าเป็น 0 และถูกนำมาใช้คำนวณด้วย
เมื่อมีการเพิ่มขอบ ขนาดที่ได้จะเป็นแบบนี้
ดังนั้นถ้าขนาดตัวกรองเป็น 3 ต้องมีการเพิ่มขอบเป็น 1 เพื่อให้อาเรย์มีขนาดเท่าเดิม แถมหากเพิ่มขอบมากกว่านี้ไปอีกขนาดของอาเรย์ก็อาจใหญ่กว่าเดิมได้ด้วย
จำนวนที่เลื่อนต่อก้าว (stride)
ในตัวอย่างที่ผ่านมาจะเป็นการเลื่อนตัวกรองไปครั้งนึงแล้วก็คำนวณทีนึง แต่ในบางครั้งเราอาจไม่ได้ต้องการคำนวณถี่ยิบหมดทุกขั้นตอนแบบนั้น คืออาจให้เลื่อนไปสัก ๒ ทีหรือมากกว่านั้นแล้วคำนวณทีนึงก็ได้ เช่นแบบนี้
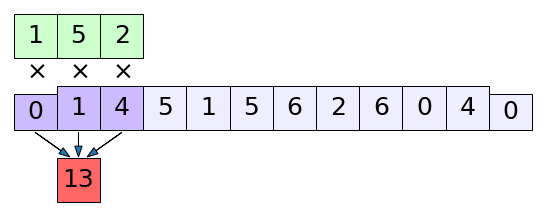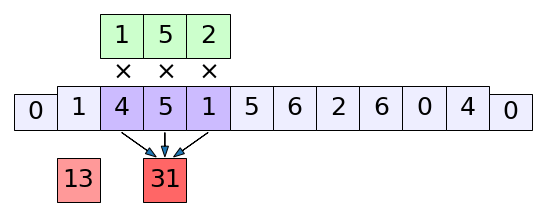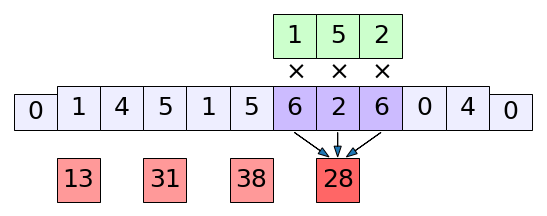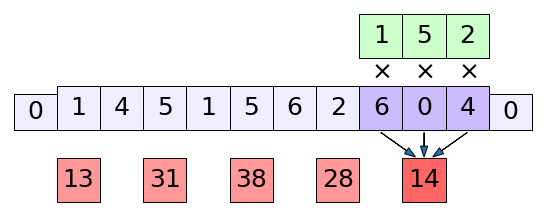
พอมีการโดดข้าม ผลที่ได้คืออาเรย์ที่มีขนาดลดลง กรณีแบบนี้ขนาดของผลลัพธ์ที่ได้จะเป็น
เพียงแต่ว่าถ้าหากในตอนที่หารจำนวนการเลื่อนแล้วมีเศษเหลือก็จะมีการปัดลง เพราะขนาดช่องยังไงก็ต้องเป็นจำนวนเต็มเท่านั้น รูปตัวอย่างนี้เองก็จะเห็นได้ว่ามีการเลื่อนไปไม่ถึงสุดขอบทางขวา
คือ (10-3+2)/2+1 = 5.5 ปัดลงเหลือ 5
อาจลองเขียนฟังก์ชันในไพธอนใหม่เพื่อให้เป็นแบบที่สามารถปรับเพิ่มขอบและปรับการเลื่อนได้แบบนี้
คอนโวลูชันใน numpy
ใน numpy เองก็มีเตรียมฟังก์ชันสำหรับทำคอนโวลูชันไว้ คือ np.convolve() เพียงแต่ว่านี่เป็นคอนโวลูชันในความหมายเดิม คือมีการกลับทิศของของตัวกรอง ส่วนคอนโวลูชันแบบที่เรากล่าวมาซึ่งไม่มีการกลับทิศนั้นจริงๆคือสหสัมพันธ์ไขว้ ซึ่งก็ทำได้โดยฟังก์ชัน np.correlate()
เพียงแต่ว่ามีความแตกต่างจากฟังก์ชันคอนโวลูชันที่เพิ่งสร้างเองไป ความสามารถน้อยกว่า คือไม่สามารถกำหนดจำนวนเลื่อนช่อง (stride) ได้ จะเลื่อนทีละช่องเท่านั้น
และการกำหนดเรื่องการเพิ่มช่องนั้นจะไม่สามารถทำได้โดยตรง แต่จะใช้การเลือกโหมด โดยใส่ค่าตัวที่ ๓ หรือคีย์เวิร์ด mode
ลองคำนวณดูเป็นตัวอย่าง แสดงความแตกต่างระหว่าง ๓ กรณี และความต่างระหว่าง np.correlate() กับ np.convolve()
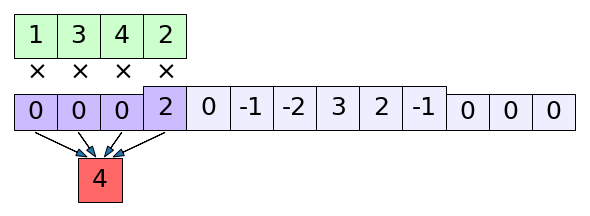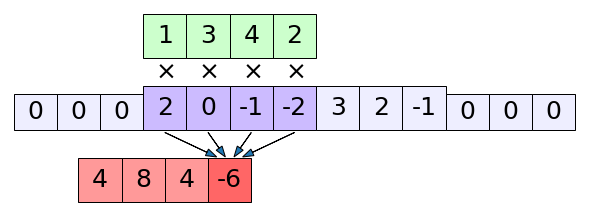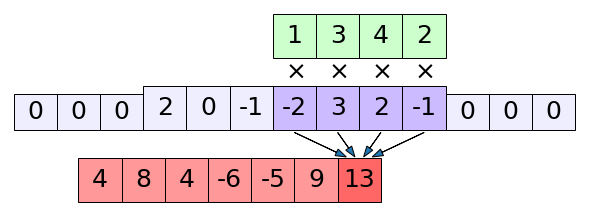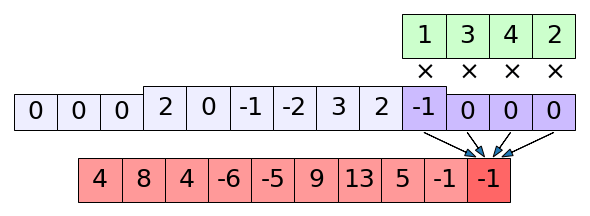
ภาพแสดง np.correlate() ในโหมด full
เปรียบเทียบกับ np.convolve() ในโหมด full เช่นกัน จะเห็นว่าตัวกรองถูกกลับด้าน
ส่วนโหมด same นั้นจะมีการเพิ่มช่องมาแค่พอให้ไม่หายไป อย่างไรก็ตามกรณีที่ขนาดตัวกรองเป็นเลขคู่แบบนี้ยังไงก็ไม่มีทางขนาดเท่าเดิมได้ ปกติจึงคำนวณเกินมาช่องนึงแล้วตัดทิ้ง
รูปนี้แสดง np.correlate() ในโหมด same เพียงแต่ว่าช่องขวาสุดจะถูกตัดทิ้ง
คอนโวลูชันในสองมิติ
ที่กล่าวมาข้างต้นเป็นคอนโวลูชันในหนึ่งมิติ แต่คอนโวลูชันสามารถทำในกี่มิติก็ได้ ในที่นี้จะอธิบายถึงคอนโวลูชันในสองมิติ ซึ่งนิยมใช้ในเรื่องของการจัดการรูปภาพ
ในคอนโวลูชันสองมิติ ทั้งอาเรย์ป้อนเข้าและตัวกรองก็จะเป็นสองมิติ ผลการคำนวณที่ได้ก็กลายเป็นสองมิติเช่นกัน อาจแสดงเป็นภาพให้เห็นได้ในลักษณะนี้
ขนาดของอาเรย์ที่ได้เป็นผลลัพธ์ออกมาจะเป็นเท่าไหร่ก็คำนวณได้เช่นเดียวกับแบบหนึ่งมิติ เพียงแต่ต้องมีการคำนวณแยกทั้งสองมิติต่างหาก
อาจเขียนฟังก์ชันคำนวณได้ดังนี้
ลองดูตัวอย่างการใช้งาน ตัวอย่างหนึ่งที่เห็นบ่อยและเข้าใจง่ายคือการใช้ทำให้ภาพเบลอ
เช่นมีภาพตัวอย่างนี้อยู่ (เพื่อความง่ายขอใช้เป็นภาพขาวดำก็พอ ภาพเอามาจาก https://phyblas.hinaboshi.com/numa40)

ลองเปิดอ่านขึ้นมาเป็นอาเรย์ของค่าสี แล้วนำมาผ่านการคอนโวลูชัน แล้วดูภาพที่ได้ออกมา
ผลที่ได้จะกลายเป็นแบบนี้

คอนโวลูชันสองมิติใน scipy
ฟังก์ชัน correlate() และ convolve() สำหรับทำคอนโวลูชันหรือสหสัมพันธ์ไขว้มิติเดียวนั้นมีใน scipy เช่นเดียวกับใน numpy สามารถใช้งานได้เหมือนกัน โดยอยู่ในมอดูลย่อย scipy.signal แต่นอกจากนี้แล้วใน scipy.signal ยังมี correlate2d() และ convolve2d() ไว้ใช้ทำคอนโวลูชันและสหสัมพันธ์ไขว้สองมิติได้ด้วย
ตัวอย่างการใช้
ได้
การทำภาพตัวอย่าง
ภาพที่แสดงตัวอย่างให้เห็นข้างต้นนั้นถูกทำขึ้นด้วยโค้ดนี้ ภาพ gif สร้างโดยวิธีการดังที่เขียนไปใน https://phyblas.hinaboshi.com/20180603
แบบหนึ่งมิติ เป็นตัวเลข
แบบเส้น
แบบสองมิติ
ประโยชน์ของคอนโวลูชัน
ทั้งหมดนี้เป็นการอธิบายว่าคอนโวลูชันคืออะไร คำนวณอย่างไร แต่พอรู้แล้วก็คงจะมีคนไม่น้อยที่สงสัยว่าการที่เอาค่ามาไล่พับทบคูณกันแบบนี้มันมีความหมายอะไร ทำไปเพื่ออะไร
ปัจจุบันคอนโวลูชันถูกนำไปประยุกต์ใช้ในเรื่องต่างๆมากมาย เช่น
- ในการจัดการรูปภาพ เช่น ทำให้ภาพเบลอหรือคมขึ้น หรือค้นหาเค้าโครง
- ในการประมวลผลสัญญาณ เช่น ลดคลื่นรบกวน ทำให้เห็นสัญญาณชัดขึ้น
- ในสวนศาสตร์ (วิชาที่ศึกษาเรื่องเสียง) เช่น จัดการกับเสียงก้อง
- ในการวิเคราะห์สเป็กโตรสโกปี เช่น วิเคราะห์การเลื่อนสเป็กตรัมจากปรากฏการณ์ดอพเลอร์
- ในทฤษฎีความน่าจะเป็น การแจกแจงความน่าจะเป็นของผลบวกของจำนวนสุ่ม ๒ ตัวที่เป็นอิสระต่อกันคือคอนโวลูชันของของการแจกแจงของแต่ละตัว
- ในการเรียนรู้ของเครื่อง เช่น เป็นส่วนประกอบของโครงข่ายประสาทเทียม
- ฯลฯ
ตัวอย่างการใช้งานบางอย่างหากมีโอกาสก็จะเขียนแสดงให้ดูต่อไป
อ้างอิง
ในบทความนี้จะอธิบายให้เห็นภาพว่าคอนโวลูชันที่ว่านี้คืออะไร โดยใช้ภาพประกอบที่เขียนจากไพธอนแสดงให้เห็นภาพชัด
ความหมายของคอนโวลูชัน
คอนโวลูชัน (convolution) หากเปิดพจนานุกรมภาษาอังกฤษก็จะพบว่ามีความหมายโดยทั่วไปว่า การบิดงอหมุนวน หรืออาจหมายถึงรอยหยักของสมองก็ได้ แต่ในทางคณิตศาสตร์แล้วมีความหมายเฉพาะอีกอย่าง
ที่จริงคอนโวลูชันมีชื่อแปลไทยว่า "สังวัตนาการ" ด้วย อย่างไรก็ตามนี่เป็นคำแปลที่แปลแล้วยากขึ้นกว่าเดิมและไม่ได้ช่วยให้เข้าใจความหมาย จึงไม่เป็นที่นิยม ในที่นี้ก็จะขอใช้ทับศัพท์
ความหมายของคอนโวลูชันนั้นหากดูแปลจีนหรือแปลญี่ปุ่น น่าจะช่วยให้เข้าใจเห็นภาพได้ชัด
ในภาษาญี่ปุ่นแปลคำนี้ว่า 畳み込み tatamikomi หมายถึงการ "พับทบแล้วอัดแน่น"
ส่วนในภาษาจีนคือ 卷积(卷積) juǎnjī หมายถึง "ม้วนแล้วกองทับถม"
ซึ่งเป็นการแปลที่อธิบายความหมายของคอนโวลูชันได้เป็นอย่างดี ทำให้แค่เห็นก็พอนึกตามได้คร่าวๆว่ามันคือการทำอะไร
อาจสรุปสั้นๆว่าเป็นการ "ม้วนทบ"
ทีนี้การม้วนทบที่ว่านี่มันคืออย่างไรกัน แค่บอกว่าม้วนทบก็คงนึกภาพไม่ออกอยู่ดีว่าการม้วนทบในทางคณิตศาสตร์นั้นมันม้วนทบยังไง
แต่ถ้าอยู่ดีๆอธิบายนิยามทางคณิตศาสตร์เลย คนทั่วไปก็เข้าใจยาก ดังนั้นขอเริ่มอธิบายด้วยภาพ
นี่คือภาพอธิบายการทำงานของคอนโวลูชัน

ตัวสีเขียวด้านบนที่วิ่งไปเรื่อยๆนี้เรียกว่าตัวกรอง (filter) แต่บางครั้งก็ถูกเรียกว่าเคอร์เนล (kernel) ส่วนสีม่วงตรงกลางคือข้อมูลป้อนเข้า
ตัวกรองจะคูณกับข้อมูลป้อนเข้าทีละส่วน แล้วเอาผลคูณมาบวกกัน ได้เป็นผลลัพธ์ด้านล่างสีแดง เสร็จแล้วก็เลื่อนตำแหน่งไปจับคู่คูณตำแหน่งถัดไปต่อ
เหมือนเรากำลังเอาตัวกรองมากลิ้งไปบนข้อมูลป้อนเข้า เพื่อจะทบแล้วอัดกันจนได้เป็นผลลัพธ์
แสดงตัวอย่างอีกภาพ อธิบายด้วยกราฟเส้นวิ่ง เส้นเขียวคือตัวกรองวิ่งไล่คำนวณคูณกับแต่ละส่วนไปเรื่อยๆ แล้วนำผลคูณทั้งหมดทุกช่องมาบวกกัน จนได้ผลออกมาเป็นกราฟข้างล่าง

อย่างไรก็ตาม สิ่งที่เรียกว่าคอนโวลูชันนั้นโดยนิยามดั้งเดิมแล้วจริงๆตัวกรองจะต้องนำมาพลิกกลับด้าน เอาส่วนท้ายไว้หน้า ผลที่ได้ก็จะต่างกัน
คือภาพจะเป็นแบบนี้แทน

ซึ่งอาจเขียนเป็นสูตรคณิตศาสตร์ได้แบบนี้
..(1)
โดย x คืออาเรย์ค่าที่ป้อนเข้า ส่วน k คือตัวกรอง
กรณีภาพแรกคือแบบไม่กลับด้านนั้นมักจะเรียกว่าสหสัมพันธ์ไขว้ (cross-correlation) คือ
..(2)
สหสัมพันธ์ไขว้ในที่นี้เป็นคนละเรื่องกับสหสัมพันธ์ (correlation) ที่เขียนถึงไปใน https://phyblas.hinaboshi.com/20180517
ในที่นี้สัญลักษณ์ ∗ แทนตัวดำเนินการคอนโวลูชัน และ ⋆ แทนสหสัมพันธ์ไขว้
และถ้าหากเป็นกรณีที่ x และ k เป็นฟังก์ชันที่มีค่าต่อเนื่อง แทนที่จะเป็นแค่ข้อมูลเป็นจุดๆ จะเขียนในรูปปริพันธ์แบบนี้
..(3)
คอนโวลูชันในโครงข่ายประสาทเทียมแบบคอนโวลูชันก็ไม่มีการกลับด้านตัวกรอง ดังนั้นจริงๆแล้วในทางเทคนิคมันคือสหสัมพันธ์ไขว้ แต่ถึงอย่างนั้นเขาก็ใช้คำว่าคอนโวลูชันกัน
ดังนั้นในที่นี้ก็จะใช้คำว่าคอนโวลูชันในความหมายนี้ด้วย ตัวกรองจะกลับด้านหรือไม่นั้นไม่ได้เป็นเรื่องที่ต้องคำนึงถึงเมื่อนำมาใช้ในบางเรื่องเช่นในโครงข่ายประสาทเทียม
ลองสร้างฟังก์ชันสำหรับทำคอนโวลูชันขึ้นในไพธอนได้ดังนี้ ตามสมการ (2)
def convo(x,k):
return np.array([sum(x[i:i+len(k)]*k) for i in range(len(x)-len(k)+1)])ตัวอย่างการใช้
x = np.array([1,3,2,5,1,0,7])
k = np.array([3,1,2])
print(convo(x,k)) # ได้ [10 21 13 16 17]เพิ่มขอบ (padding)
โดยปกติแล้วเมื่อทำการคอนโวลูชัน ผลที่ได้ออกมาจะเป็นอาเรย์ที่มีขนาดเล็กลง โดยที่
เพราะฉะนั้นเมื่อใช้ตัวกรองขนาด 3 ก็จะทำให้อาเรย์ที่ได้เล็กลงไป 2
แต่ว่าบ่อยครั้งที่เราอาจไม่ต้องการให้ขนาดของผลที่ได้มีการเปลี่ยนแปลง กรณีแบบนี้โดยทั่วไปจะทำได้โดยการเพิ่มขอบลงไปก่อนที่จะทำการคอนโวลูชัน
ดูรูปนี้จะเข้าใจง่ายขึ้น มีส่วนขอบที่เพิ่มเข้ามาทางซ้ายขวา โดยจะมีค่าเป็น 0 และถูกนำมาใช้คำนวณด้วย

เมื่อมีการเพิ่มขอบ ขนาดที่ได้จะเป็นแบบนี้
ดังนั้นถ้าขนาดตัวกรองเป็น 3 ต้องมีการเพิ่มขอบเป็น 1 เพื่อให้อาเรย์มีขนาดเท่าเดิม แถมหากเพิ่มขอบมากกว่านี้ไปอีกขนาดของอาเรย์ก็อาจใหญ่กว่าเดิมได้ด้วย
จำนวนที่เลื่อนต่อก้าว (stride)
ในตัวอย่างที่ผ่านมาจะเป็นการเลื่อนตัวกรองไปครั้งนึงแล้วก็คำนวณทีนึง แต่ในบางครั้งเราอาจไม่ได้ต้องการคำนวณถี่ยิบหมดทุกขั้นตอนแบบนั้น คืออาจให้เลื่อนไปสัก ๒ ทีหรือมากกว่านั้นแล้วคำนวณทีนึงก็ได้ เช่นแบบนี้

พอมีการโดดข้าม ผลที่ได้คืออาเรย์ที่มีขนาดลดลง กรณีแบบนี้ขนาดของผลลัพธ์ที่ได้จะเป็น
เพียงแต่ว่าถ้าหากในตอนที่หารจำนวนการเลื่อนแล้วมีเศษเหลือก็จะมีการปัดลง เพราะขนาดช่องยังไงก็ต้องเป็นจำนวนเต็มเท่านั้น รูปตัวอย่างนี้เองก็จะเห็นได้ว่ามีการเลื่อนไปไม่ถึงสุดขอบทางขวา
คือ (10-3+2)/2+1 = 5.5 ปัดลงเหลือ 5
อาจลองเขียนฟังก์ชันในไพธอนใหม่เพื่อให้เป็นแบบที่สามารถปรับเพิ่มขอบและปรับการเลื่อนได้แบบนี้
def convo(x,k,s=1,p=0):
if(p):
x = np.hstack([np.zeros(p),x,np.zeros(p)])
return np.array([sum(x[i:i+len(k)]*k) for i in range(0,len(x)-len(k)+1,s)])
x = np.array([3,5,7,1,2.1,0,3,4])
k = np.array([4,1,3])
print(convo(x,k,1,0)) # ได้ [38. 30. 35.3 6.1 17.4 15. ]
print(convo(x,k,2,0)) # ได้ [38. 35.3 17.4]
print(convo(x,k,1,1)) # ได้ [18. 38. 30. 35.3 6.1 17.4 15. 16. ]คอนโวลูชันใน numpy
ใน numpy เองก็มีเตรียมฟังก์ชันสำหรับทำคอนโวลูชันไว้ คือ np.convolve() เพียงแต่ว่านี่เป็นคอนโวลูชันในความหมายเดิม คือมีการกลับทิศของของตัวกรอง ส่วนคอนโวลูชันแบบที่เรากล่าวมาซึ่งไม่มีการกลับทิศนั้นจริงๆคือสหสัมพันธ์ไขว้ ซึ่งก็ทำได้โดยฟังก์ชัน np.correlate()
เพียงแต่ว่ามีความแตกต่างจากฟังก์ชันคอนโวลูชันที่เพิ่งสร้างเองไป ความสามารถน้อยกว่า คือไม่สามารถกำหนดจำนวนเลื่อนช่อง (stride) ได้ จะเลื่อนทีละช่องเท่านั้น
และการกำหนดเรื่องการเพิ่มช่องนั้นจะไม่สามารถทำได้โดยตรง แต่จะใช้การเลือกโหมด โดยใส่ค่าตัวที่ ๓ หรือคีย์เวิร์ด mode
| full | ตัวกรองจะวิ่งตั้งแต่จุดที่เริ่มซ้อนกันแค่ช่องเดียว โดยมีการเพิ่มช่อง ผลที่ได้จะเป็นอาเรย์ขนาดใหญ่ขึ้น |
| valid | ตัวกรองจะวิ่งแค่ภายในขอบเขตที่ซ้อนกันทุกช่อง ไม่มีการเพิ่มช่อง ผลที่ได้จะเป็นอาเรย์ขนาดเล็กลง |
| same | ตัวกรองจะเริ่มวิ่งจากที่ซ้อนกันส่วนหนึ่ง โดยจะเพิ่มช่องเพื่อรักษาให้จำนวนอาเรย์ที่ได้เท่ากับอาเรย์ที่ป้อนเข้า |
ลองคำนวณดูเป็นตัวอย่าง แสดงความแตกต่างระหว่าง ๓ กรณี และความต่างระหว่าง np.correlate() กับ np.convolve()
x = np.array([2,0,-1,-2,3,2,-1])
k = np.array([1,3,4,2])
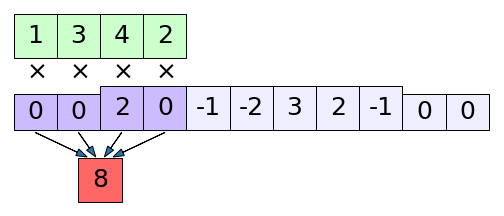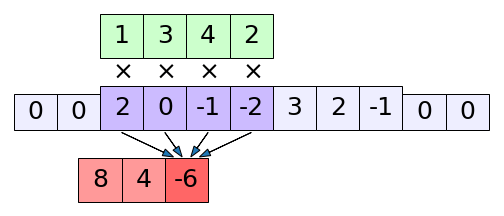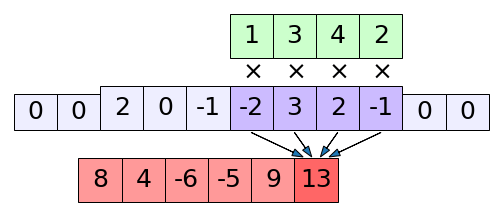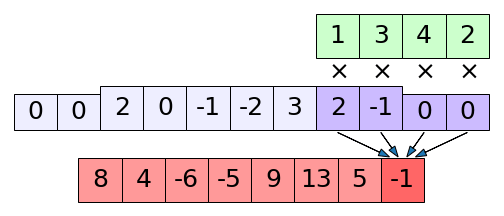
print(np.correlate(x,k,'full')) # ได้ [ 4 8 4 -6 -5 9 13 5 -1 -1]
print(np.correlate(x,k,'valid')) # ได้ [-6 -5 9 13]
print(np.correlate(x,k,'same')) # ได้ [ 8 4 -6 -5 9 13 5]
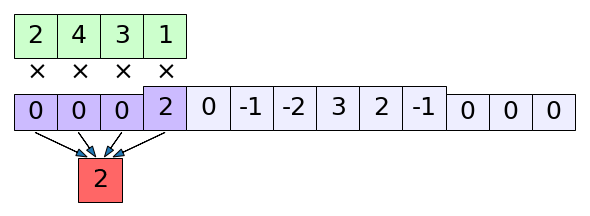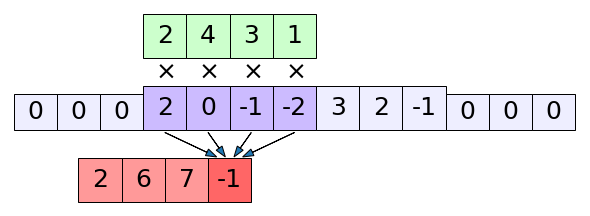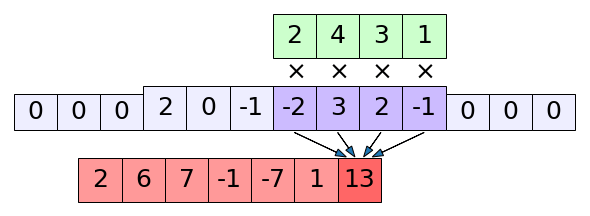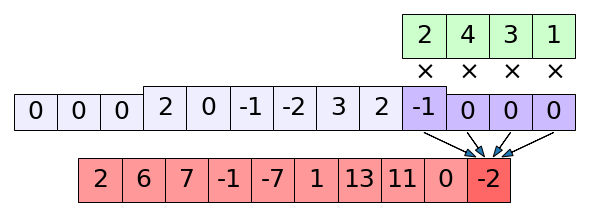
print(np.convolve(x,k,'full')) # ได้ [ 2 6 7 -1 -7 1 13 11 0 -2]
print(np.convolve(x,k,'valid')) # ได้ [-1 -7 1 13]
print(np.convolve(x,k,'same')) # ได้ [ 6 7 -1 -7 1 13 11]ภาพแสดง np.correlate() ในโหมด full

เปรียบเทียบกับ np.convolve() ในโหมด full เช่นกัน จะเห็นว่าตัวกรองถูกกลับด้าน

ส่วนโหมด same นั้นจะมีการเพิ่มช่องมาแค่พอให้ไม่หายไป อย่างไรก็ตามกรณีที่ขนาดตัวกรองเป็นเลขคู่แบบนี้ยังไงก็ไม่มีทางขนาดเท่าเดิมได้ ปกติจึงคำนวณเกินมาช่องนึงแล้วตัดทิ้ง
รูปนี้แสดง np.correlate() ในโหมด same เพียงแต่ว่าช่องขวาสุดจะถูกตัดทิ้ง

คอนโวลูชันในสองมิติ
ที่กล่าวมาข้างต้นเป็นคอนโวลูชันในหนึ่งมิติ แต่คอนโวลูชันสามารถทำในกี่มิติก็ได้ ในที่นี้จะอธิบายถึงคอนโวลูชันในสองมิติ ซึ่งนิยมใช้ในเรื่องของการจัดการรูปภาพ
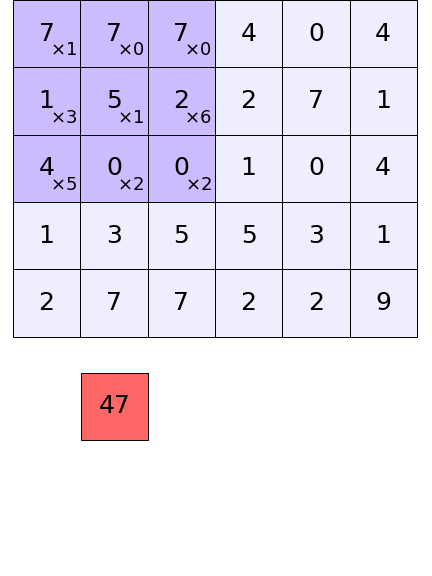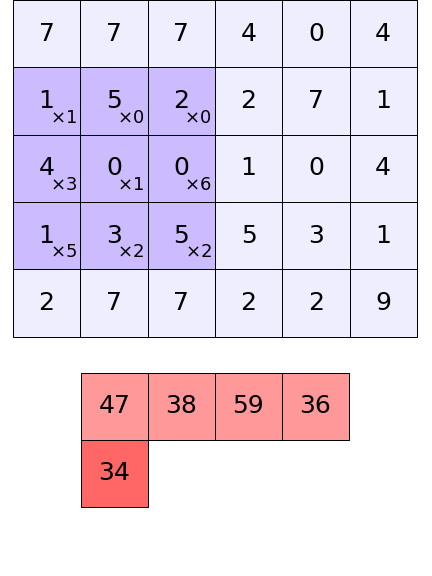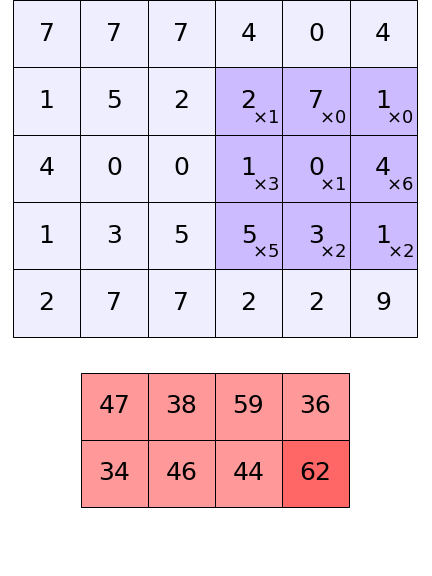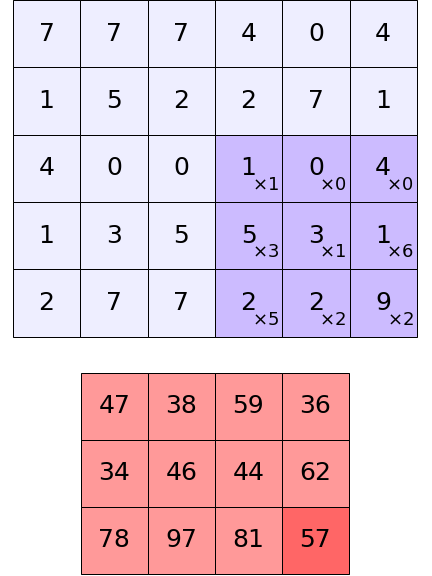
ในคอนโวลูชันสองมิติ ทั้งอาเรย์ป้อนเข้าและตัวกรองก็จะเป็นสองมิติ ผลการคำนวณที่ได้ก็กลายเป็นสองมิติเช่นกัน อาจแสดงเป็นภาพให้เห็นได้ในลักษณะนี้

ขนาดของอาเรย์ที่ได้เป็นผลลัพธ์ออกมาจะเป็นเท่าไหร่ก็คำนวณได้เช่นเดียวกับแบบหนึ่งมิติ เพียงแต่ต้องมีการคำนวณแยกทั้งสองมิติต่างหาก
อาจเขียนฟังก์ชันคำนวณได้ดังนี้
def convo2d(x,k,s=1,p=0):
nx = x.shape
nk = k.shape
if(p):
if(type(p)==int):
p = p,p
nx = nx[0]+2*p[0],nx[1]+2*p[1]
x0 = np.zeros(nx)
x0[p[0]:nx[0]-p[0],p[1]:nx[1]-p[1]] = x
x = x0
if(type(s)==int):
s = s,s
return np.array([[(x[i:i+nk[0],j:j+nk[1]]*k).sum()
for j in range(0,nx[1]-nk[1]+1,s[1])]
for i in range(0,nx[0]-nk[0]+1,s[0])])ลองดูตัวอย่างการใช้งาน ตัวอย่างหนึ่งที่เห็นบ่อยและเข้าใจง่ายคือการใช้ทำให้ภาพเบลอ
เช่นมีภาพตัวอย่างนี้อยู่ (เพื่อความง่ายขอใช้เป็นภาพขาวดำก็พอ ภาพเอามาจาก https://phyblas.hinaboshi.com/numa40)

ลองเปิดอ่านขึ้นมาเป็นอาเรย์ของค่าสี แล้วนำมาผ่านการคอนโวลูชัน แล้วดูภาพที่ได้ออกมา
x = imageio.imread('c40a08.png')[:,:,0]
k = np.ones([5,5])
y = convo2d(x,k)
plt.figure(figsize=[5,6])
plt.axes([0,0,1,1])
plt.imshow(y,cmap='gray')
plt.axis('off')
plt.show()ผลที่ได้จะกลายเป็นแบบนี้

คอนโวลูชันสองมิติใน scipy
ฟังก์ชัน correlate() และ convolve() สำหรับทำคอนโวลูชันหรือสหสัมพันธ์ไขว้มิติเดียวนั้นมีใน scipy เช่นเดียวกับใน numpy สามารถใช้งานได้เหมือนกัน โดยอยู่ในมอดูลย่อย scipy.signal แต่นอกจากนี้แล้วใน scipy.signal ยังมี correlate2d() และ convolve2d() ไว้ใช้ทำคอนโวลูชันและสหสัมพันธ์ไขว้สองมิติได้ด้วย
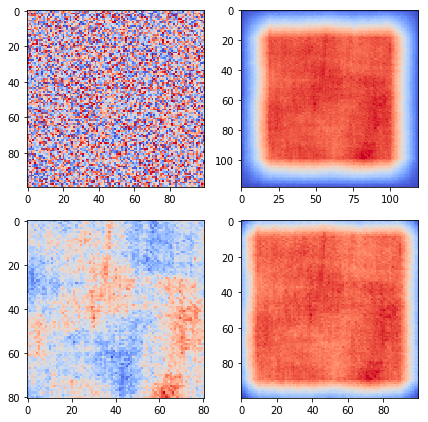
ตัวอย่างการใช้
from scipy.signal import correlate2d
x = np.random.random([100,100])
k = np.random.random([20,20])
plt.figure(figsize=[6,6])
plt.subplot(221)
plt.imshow(x,cmap='coolwarm')
plt.subplot(222)
plt.imshow(correlate2d(x,k,'full'),cmap='coolwarm')
plt.subplot(223)
plt.imshow(correlate2d(x,k,'valid'),cmap='coolwarm')
plt.subplot(224)
plt.imshow(correlate2d(x,k,'same'),cmap='coolwarm')
plt.tight_layout()
plt.show()ได้

การทำภาพตัวอย่าง
ภาพที่แสดงตัวอย่างให้เห็นข้างต้นนั้นถูกทำขึ้นด้วยโค้ดนี้ ภาพ gif สร้างโดยวิธีการดังที่เขียนไปใน https://phyblas.hinaboshi.com/20180603
แบบหนึ่งมิติ เป็นตัวเลข
import imageio
def laiconvo(c,x,k,s=1,p=0):
if(p):
x = np.hstack([np.zeros(p),x,np.zeros(p)])
nx = len(x)
nk = len(k)
phap = []
for j in range(0,nx-nk+1,s):
fig = plt.figure(figsize=[(nx*3+2)/5.,3])
ax = plt.axes([0,0,1,1],aspect=1,xlim=[0,nx*3+0.1],ylim=[-6,9])
for i in range(nx):
if(j<=i<nk+j):
fc = '#ccbbff'
else:
fc = '#eeeeff'
pad = (i<p)|(nx-i<=p)
ax.add_patch(plt.Rectangle([i*3,0],3,3-pad*0.5,ec='k',fc=fc))
ax.text(i*3+1.5,1.5-pad*0.25,'%d'%x[i],va='center',ha='center',size=25)
for i in range(nk):
ax.add_patch(plt.Rectangle([(i+j)*3,5],3,3,ec='k',fc='#ccffcc'))
ax.text((i+j)*3+1.5,6.5,'%d'%k[i],va='center',ha='center',size=25)
ax.text((i+j)*3+1.5,4,r'$\times$',va='center',ha='center',size=25)
plt.arrow((i+j)*3+1.5,-0.2,((1.5*(nk-1))-i*3)*0.8,-1.7,head_width=0.5,length_includes_head=1)
for i in range(0,j+1,s):
if(i==j):
fc = '#ff6666'
else:
fc = '#ff9999'
v = (x[i:i+nk]*k).sum()
ax.add_patch(plt.Rectangle([i*3+(1.5*(nk-1)),-5],3,3,ec='k',fc=fc))
ax.text((i*3+1.5*(nk-1))+1.5,-3.5,'%d'%v,va='center',ha='center',size=25)
plt.axis('off')
fig.canvas.draw()
phap.append(np.array(fig.canvas.renderer._renderer))
plt.close()
imageio.mimsave(c,phap,fps=2.5)
x = np.random.randint(0,7,10)
k = np.random.randint(0,7,3)
laiconvo('e01.gif',x,k,1,0)แบบเส้น
def senconvo(c,x,k):
nx = len(x)
nk = len(k)
x2 = np.array([sum(x[i:i+nk]*k) for i in range(0,nx-nk+1)])
nx2 = len(x2)
phap = []
for i in range(0,nx2,max(1,int(nx2/50))):
fig = plt.figure(figsize=[5,3])
ax = plt.axes([0.1,0.3,0.9,0.7],xlim=[0,nx-1],ylim=[x.min()-x.std()*0.2,x.max()+x.std()*0.2],xticks=[])
ax.spines['top'].set_visible(0)
ax.spines['right'].set_visible(0)
plt.plot(np.arange(nx),x,'#6677aa',alpha=0.2)
plt.plot(np.arange(nx)[:i+nk],x[:i+nk],'#6677aa')
plt.plot(np.arange(i,i+nk),k,'#66aa66')
plt.axvspan(i,i+nk-1,alpha=0.2,fc='#ddffdd',lw=3,ec='k')
ax = plt.axes([0.1,0,0.9,0.3],xlim=[0,nx-1],ylim=[x2.min()-x2.std()*0.2,x2.max()+x2.std()*0.2],xticks=[])
ax.spines['right'].set_visible(0)
ax.spines['bottom'].set_visible(0)
plt.plot((np.arange(0,i+1)),x2[:i+1],'#aa3333')
plt.plot([i,i],[x2[i],x2.max()+x2.std()*0.2],'k',lw=3,alpha=0.2)
fig.canvas.draw()
phap.append(np.array(fig.canvas.renderer._renderer))
plt.close()
imageio.mimsave(c,phap,duration=0.04)
x = np.random.normal(0,0.1,100).cumsum()
x -= np.linspace(0,x[-1],100)
x **= 3
k = np.random.normal(0,0.01,10).cumsum()
senconvo('e02.gif',x,k)แบบสองมิติ
def laiconvo2d(c,x,k,s=1,p=0):
nx = x.shape
nk = k.shape
if(p):
if(type(p)==int):
p = p,p
nx = nx[0]+2*p[0],nx[1]+2*p[1]
x0 = np.zeros(nx)
x0[p[0]:nx[0]-p[0],p[1]:nx[1]-p[1]] = x
x = x0
if(type(s)==int):
s = s,s
nx2 = nx[0]-nk[0]+1,nx[1]-nk[1]+1
phap = []
for n in range(0,nx2[0],s[0]):
for m in range(0,nx2[1],s[1]):
fig = plt.figure(figsize=[nx[1],nx[0]+nx2[0]])
ax = plt.axes([0,(nx2[0]+0.5)/(nx[0]+nx2[0]+0.5),1,nx[0]/(nx[0]+nx2[0]+0.5)],aspect=1,xlim=[0,nx[1]*3+0.1],ylim=[-nx[0]*3-0.1,0])
ax2 =plt.axes([0,0,1,nx2[0]/(nx[0]+nx2[0]+0.5)],aspect=1,xlim=[0,nx2[1]*3+0.1],ylim=[-nx2[0]*3-0.1,0])
for j in range(nx[0]):
for i in range(nx[1]):
if(m<=i<nk[1]+m and n<=j<nk[0]+n):
fc = '#ccbbff'
else:
fc = '#eeeeff'
ax.add_patch(plt.Rectangle([i*3,-j*3-3],3,3,ec='k',fc=fc))
ax.text(i*3+1.5,-j*3-1.5,'%d'%x[j,i],va='center',ha='center',size=25)
for j in range(nk[0]):
for i in range(nk[1]):
ax.text((m+i)*3+2.25,-(n+j)*3-2.25,'$\\times%d$'%k[j,i],va='center',ha='center',size=18)
for j in range(0,nx2[0],s[0]):
for i in range(0,nx2[1],s[1]):
if(nx2[1]*j+i>nx2[1]*n+m):
break
if(i==m and j==n):
fc = '#ff6666'
else:
fc = '#ff9999'
ax2.add_patch(plt.Rectangle([i*3,-j*3-3],3,3,ec='k',fc=fc))
ax2.text(i*3+1.5,-j*3-1.5,'%d'%((x[j:j+nk[0],i:i+nk[1]]*k).sum()),va='center',ha='center',size=25)
ax.axis('off')
ax2.axis('off')
fig.canvas.draw()
phap.append(np.array(fig.canvas.renderer._renderer))
plt.close()
imageio.mimsave(c,phap,fps=2.5)
x = np.random.randint(0,10,[5,6])
k = np.random.randint(0,10,[3,3])
laiconvo2d('e09.gif',x,k,1,[0,0])ประโยชน์ของคอนโวลูชัน
ทั้งหมดนี้เป็นการอธิบายว่าคอนโวลูชันคืออะไร คำนวณอย่างไร แต่พอรู้แล้วก็คงจะมีคนไม่น้อยที่สงสัยว่าการที่เอาค่ามาไล่พับทบคูณกันแบบนี้มันมีความหมายอะไร ทำไปเพื่ออะไร
ปัจจุบันคอนโวลูชันถูกนำไปประยุกต์ใช้ในเรื่องต่างๆมากมาย เช่น
- ในการจัดการรูปภาพ เช่น ทำให้ภาพเบลอหรือคมขึ้น หรือค้นหาเค้าโครง
- ในการประมวลผลสัญญาณ เช่น ลดคลื่นรบกวน ทำให้เห็นสัญญาณชัดขึ้น
- ในสวนศาสตร์ (วิชาที่ศึกษาเรื่องเสียง) เช่น จัดการกับเสียงก้อง
- ในการวิเคราะห์สเป็กโตรสโกปี เช่น วิเคราะห์การเลื่อนสเป็กตรัมจากปรากฏการณ์ดอพเลอร์
- ในทฤษฎีความน่าจะเป็น การแจกแจงความน่าจะเป็นของผลบวกของจำนวนสุ่ม ๒ ตัวที่เป็นอิสระต่อกันคือคอนโวลูชันของของการแจกแจงของแต่ละตัว
- ในการเรียนรู้ของเครื่อง เช่น เป็นส่วนประกอบของโครงข่ายประสาทเทียม
- ฯลฯ
ตัวอย่างการใช้งานบางอย่างหากมีโอกาสก็จะเขียนแสดงให้ดูต่อไป
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy-- คณิตศาสตร์
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> scipy