[python] สร้างเส้นโค้งฮิลแบร์ทสองมิติ
เขียนเมื่อ 2018/07/14 13:59
แก้ไขล่าสุด 2024/02/22 10:53
ช่วงนี้พยายามศึกษาความรู้เพิ่มเติมทางคณิตศาสตร์อยู่ ขณะพยายามเข้าใจเรื่องปริภูมฮิลแบร์ทก็ไปเจอเรื่องที่เกี่ยวข้องที่น่าสนใจเข้า คือเส้นโค้งฮิลแบร์ท
เกี่ยวกับเรื่องนี้มีเขียนอยู่ในวิกิ
https://th.wikipedia.org/wiki/เส้นโค้งฮิลแบร์ท
เส้นโค้งฮิลแบร์ทเป็นแฟร็กทัลรูปแบบหนึ่งที่มีลักษณะน่าสนใจ
เมื่อก่อนก็เคยทำแฟรกทัลที่มีรูปแบบตามใจตัวเองมาแล้ว https://phyblas.hinaboshi.com/20170223
ในวิกิพีเดียมีลงอัลกอริธึมสำหรับการสร้างไว้ด้วย ซึ่งเขียนโดยใช้ระบบลินเดินไมเยอร์ (Lindenmayer) หรือเรียกย่อๆว่าระบบ L ดังนั้นจึงนำมาเขียนโปรแกรมได้เลย
แนวคิดคือ ให้เริ่มจากสร้างรหัสควบคุมที่ในการลากเส้น ว่าจะทำการเปลี่ยนมุม หรือวาดตรงไป จากนั้นกำหนดรหัสเริ่มต้น แล้วก็ค่อยๆวนซ้ำเพื่อแทนที่รหัสที่มีอยู่เดิมตามกฎเกณฑ์ ทำไปเรื่อยๆจนครบตามอันดับที่ต้องการ แล้วสุดท้ายจึงนำรหัสที่ได้มาแปลงเป็นตำแหน่งของจุดที่จะลาก
รหัสที่ใช้มีดังนี้
ในที่นี้ -2 และ 2 คือจุดที่เวลาทำซ้ำจะให้แทนที่ โดยมีกฎเกณฑ์ดังนี้
-2 => -1,2,0,1,-2,0,-2,1,0,2,-1
2 => 1,-2,0,-1,2,0,2,-1,0,-2,1
โดยเริ่มต้นจะเริ่มจาก -2 ตัวเดียว จากนั้นก็ทำวนซ้ำแล้วแทนที่ไปเรื่อยๆ
รหัส -2 และ 2 นั้นมีไว้เพื่อถูกแทนที่ตอนแปลงเป็นอันดับต่อไปเท่านั้น เมื่อคราวนำมาแปลงเป็นตำแหน่งจะไม่ถูกพิจารณา
ส่วนรหัส -1 และ 1 คือสั่งให้หันซ้ายหรือขวานั้น จะนำไปแปลงเป็นทิศทาง ซึ่งเปลี่ยนไปในแต่ละครั้งที่มีคำสั่ง ทิศขวา, บน, ซ้าย, ล่าง แทนด้วยค่า 0, 1, 2, 3 ถ้าสั่งเลี้ยวขวาค่าก็เพิ่มขึ้น 1 สั่งเลี้ยวซ้ายก็ลดลง 1 แต่ถ้าค่ากลายเป็น 4 ก็จะแปลงให้เหลือ 0 ถ้ากลายเป็น -1 ก็จะกลับมาเป็น 3
ส่วน 0 เป็นคำสั่งให้วาดจุดต่อไปโดยมุ่งหน้าไปยังทิศที่หันอยู่
สามารถเขียนเป็นโค้ดได้แบบนี้
ก็จะได้ภาพแบบนี้ออกมา

เพื่อความเป็นระเบียบอาจเขียนใหม่เป็นฟังก์ชัน โดยภายในใช้ฟังก์ชันเวียนเกิด (รายละเอียดอ่านได้ใน https://phyblas.hinaboshi.com/tsuchinoko20)
ฟังก์ชันจะแบ่งออกเป็นสองส่วน คือส่วนสร้างรหัส และส่วนแปลงรหัสเป็นตำแหน่ง
ลองนำฟังก์ชันที่สร้างมาใช้
ก็จะได้ภาพแบบเดิมออกมา
เพื่อให้เห็นภาพชัด ลองทำให้เปลี่ยนสีไปเรื่อยๆตามลำดับสายรุ้ง ไล่ตั้งแต่อันดับ 1 ถึง 7
ก็จะได้ภาพเหล่านี้ออกมา
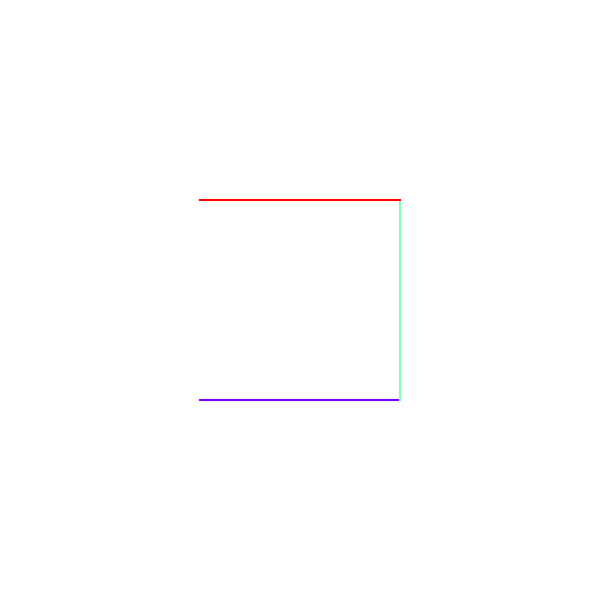
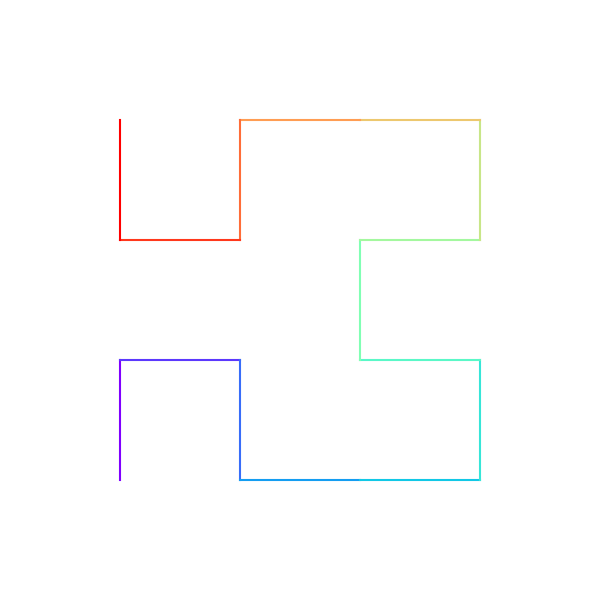




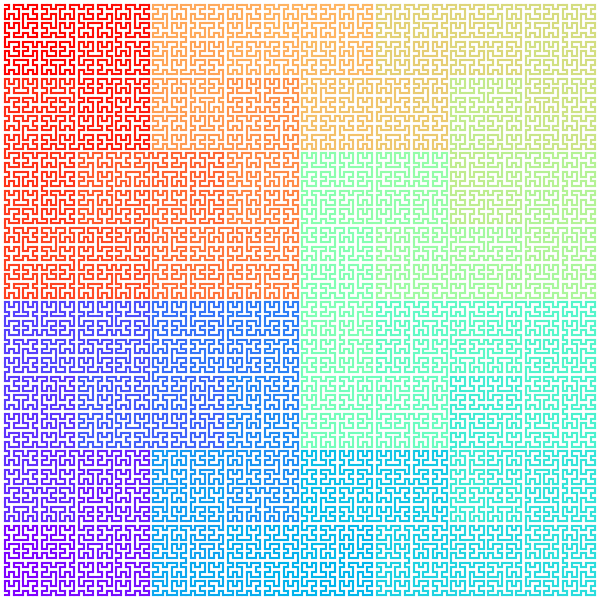
จากนั้นลองเอามาทำเป็นภาพเคลื่อนไหวดู โดยใส่ฉากหลังไว้ แล้วค่อยๆวาดเส้นให้เห็นพื้นที่ที่ถูกวาดไปเรื่อยๆ
ภาพฉากหลังเอามาจาก https://www.pixiv.net/artworks/67137373

ผลออกมาก็จะได้ภาพเป็นลำดับขั้นตอนออกมา 1023 ภาพ และนี่เป็นหนึ่งในนั้น

จากนั้นก็เอาภาพที่ได้ทั้งหมดมาประกอบเป็นวีดีโออีกที ผลที่ได้ลงเอาไว้ใน facebook เข้าไปดูได้ >> https://www.facebook.com/ikamiso/videos/1746538728776466
นอกจากนี้ยังได้ลองเอามาสร้างเป็นแบบจำลองสามมิติของทางวงกดขึ้นมาในมายาด้วย ตัวโค้ดได้แจกไว้ใน https://github.com/phyblas/yamimayapython/blob/master/tham_khong_tangtang/wongkot/wongkot_hilbert.py
กลายเป็นเส้นทางที่ต้องเดินคดเคี้ยวต่อเนื่องตลอดตั้งแต่ทางเข้าไปจนถึงทางออกแบบนี้

เกี่ยวกับเรื่องนี้มีเขียนอยู่ในวิกิ
https://th.wikipedia.org/wiki/เส้นโค้งฮิลแบร์ท
เส้นโค้งฮิลแบร์ทเป็นแฟร็กทัลรูปแบบหนึ่งที่มีลักษณะน่าสนใจ
เมื่อก่อนก็เคยทำแฟรกทัลที่มีรูปแบบตามใจตัวเองมาแล้ว https://phyblas.hinaboshi.com/20170223
ในวิกิพีเดียมีลงอัลกอริธึมสำหรับการสร้างไว้ด้วย ซึ่งเขียนโดยใช้ระบบลินเดินไมเยอร์ (Lindenmayer) หรือเรียกย่อๆว่าระบบ L ดังนั้นจึงนำมาเขียนโปรแกรมได้เลย
แนวคิดคือ ให้เริ่มจากสร้างรหัสควบคุมที่ในการลากเส้น ว่าจะทำการเปลี่ยนมุม หรือวาดตรงไป จากนั้นกำหนดรหัสเริ่มต้น แล้วก็ค่อยๆวนซ้ำเพื่อแทนที่รหัสที่มีอยู่เดิมตามกฎเกณฑ์ ทำไปเรื่อยๆจนครบตามอันดับที่ต้องการ แล้วสุดท้ายจึงนำรหัสที่ได้มาแปลงเป็นตำแหน่งของจุดที่จะลาก
รหัสที่ใช้มีดังนี้
| -2 | รอแทนที่ |
| -1 | หันซ้าย |
| 0 | วาดตรงไป |
| 1 | หันขวา |
| 2 | รอแทนที่ |
ในที่นี้ -2 และ 2 คือจุดที่เวลาทำซ้ำจะให้แทนที่ โดยมีกฎเกณฑ์ดังนี้
-2 => -1,2,0,1,-2,0,-2,1,0,2,-1
2 => 1,-2,0,-1,2,0,2,-1,0,-2,1
โดยเริ่มต้นจะเริ่มจาก -2 ตัวเดียว จากนั้นก็ทำวนซ้ำแล้วแทนที่ไปเรื่อยๆ
รหัส -2 และ 2 นั้นมีไว้เพื่อถูกแทนที่ตอนแปลงเป็นอันดับต่อไปเท่านั้น เมื่อคราวนำมาแปลงเป็นตำแหน่งจะไม่ถูกพิจารณา
ส่วนรหัส -1 และ 1 คือสั่งให้หันซ้ายหรือขวานั้น จะนำไปแปลงเป็นทิศทาง ซึ่งเปลี่ยนไปในแต่ละครั้งที่มีคำสั่ง ทิศขวา, บน, ซ้าย, ล่าง แทนด้วยค่า 0, 1, 2, 3 ถ้าสั่งเลี้ยวขวาค่าก็เพิ่มขึ้น 1 สั่งเลี้ยวซ้ายก็ลดลง 1 แต่ถ้าค่ากลายเป็น 4 ก็จะแปลงให้เหลือ 0 ถ้ากลายเป็น -1 ก็จะกลับมาเป็น 3
ส่วน 0 เป็นคำสั่งให้วาดจุดต่อไปโดยมุ่งหน้าไปยังทิศที่หันอยู่
สามารถเขียนเป็นโค้ดได้แบบนี้
import numpy as np
import matplotlib.pyplot as plt
andap = 8 # อันดับ
# สร้างรหัส
lis_rahat = [-2] # รหัสเริ่มต้น
for i in range(andap):
lis_rahat_mai = []
for rahat in lis_rahat: # ทำซ้ำโดยเอารหัสจากอันดับที่แล้วมาแปลง
if(rahat==-2):
lis_rahat_mai.extend([-1,2,0,1,-2,0,-2,1,0,2,-1])
elif(rahat==2):
lis_rahat_mai.extend([1,-2,0,-1,2,0,2,-1,0,-2,1])
else:
lis_rahat_mai.extend([rahat])
lis_rahat = lis_rahat_mai
# ทำการแปลงรหัสเป็นตำแหน่ง
tamnaeng = [(0,0)] # ตำแหน่งเริ่มต้น
thit = 1
for rahat in lis_rahat: # ไล่อ่านรหัสทีละตัว
if(rahat==0): # 0: ทำการเคลื่อนย้าย
x = tamnaeng[-1][0]+(thit==0)-(thit==2)
y = tamnaeng[-1][1]+(thit==1)-(thit==3)
tamnaeng.append((x,y)) # บันทึกตำแหน่งใหม่
elif(rahat==-1 or rahat==1): # หันซ้ายหรือขวา
thit += rahat
thit %= 4
xy = np.array(tamnaeng)
x,y = xy.T
plt.figure(figsize=[6.4,6.4])
plt.axes([0,0,1,1],aspect=1,xlim=[-0.5,2**andap-0.5],ylim=[-0.5,2**andap-0.5])
plt.plot(x,y,'#FF6666',lw=0.5)
plt.axis('off')
plt.show()ก็จะได้ภาพแบบนี้ออกมา

เพื่อความเป็นระเบียบอาจเขียนใหม่เป็นฟังก์ชัน โดยภายในใช้ฟังก์ชันเวียนเกิด (รายละเอียดอ่านได้ใน https://phyblas.hinaboshi.com/tsuchinoko20)
ฟังก์ชันจะแบ่งออกเป็นสองส่วน คือส่วนสร้างรหัส และส่วนแปลงรหัสเป็นตำแหน่ง
def hilbert(andap,thit):
# สร้างรหัส
def sang_rahat(andap):
if(andap==0):
return [-2] # รหัสเริ่มต้น
else:
lis_rahat = []
for rahat in sang_rahat(andap-1): # เวียนเกิดโดยเอารหัสจากอันดับที่แล้วมาแปลง
if(rahat==-2):
lis_rahat.extend([-1,2,0,1,-2,0,-2,1,0,2,-1])
elif(rahat==2):
lis_rahat.extend([1,-2,0,-1,2,0,2,-1,0,-2,1])
else:
lis_rahat.extend([rahat])
return lis_rahat
# ทำการแปลงรหัสเป็นตำแหน่ง
def plaeng_rahat(lis_rahat,thit):
'''thit = ทิศ
0: ขวา
1: บน
2: ซ้าย
3: ล่าง
'''
tamnaeng = [(0,0)] # ตำแหน่งเริ่มต้น
for rahat in lis_rahat: # ไล่อ่านรหัสทีละตัว
if(rahat==0): # 0: ทำการเคลื่อนย้าย
x = tamnaeng[-1][0]+(thit==0)-(thit==2)
y = tamnaeng[-1][1]+(thit==1)-(thit==3)
tamnaeng.append((x,y)) # บันทึกตำแหน่งใหม่
elif(rahat==-1 or rahat==1): # หันซ้ายหรือขวา
thit += rahat
thit %= 4
return tamnaeng
lis_rahat = sang_rahat(andap)
return plaeng_rahat(lis_rahat,thit)ลองนำฟังก์ชันที่สร้างมาใช้
andap = 8
xy = np.array(hilbert(andap,1))
x,y = xy.T
plt.figure(figsize=[6.4,6.4])
plt.axes([0,0,1,1],aspect=1,xlim=[-0.5,2**andap-0.5],ylim=[-0.5,2**andap-0.5])
plt.plot(x,y,'#FF6666',lw=0.5)
plt.axis('off')
plt.show()ก็จะได้ภาพแบบเดิมออกมา
เพื่อให้เห็นภาพชัด ลองทำให้เปลี่ยนสีไปเรื่อยๆตามลำดับสายรุ้ง ไล่ตั้งแต่อันดับ 1 ถึง 7
for n in range(1,8):
xy = np.array(hilbert(n,1))
plt.figure(figsize=[6,6])
plt.axes([0,0,1,1],aspect=1,xlim=[-1,2**n],ylim=[-1,2**n])
c = plt.get_cmap('rainbow')(np.linspace(0,1,len(xy)-1))
for i in range(len(xy)-1):
plt.plot(xy[i:i+2,0],xy[i:i+2,1],color=c[i])
plt.axis('off')
plt.savefig('h%d'%n)
plt.close()ก็จะได้ภาพเหล่านี้ออกมา
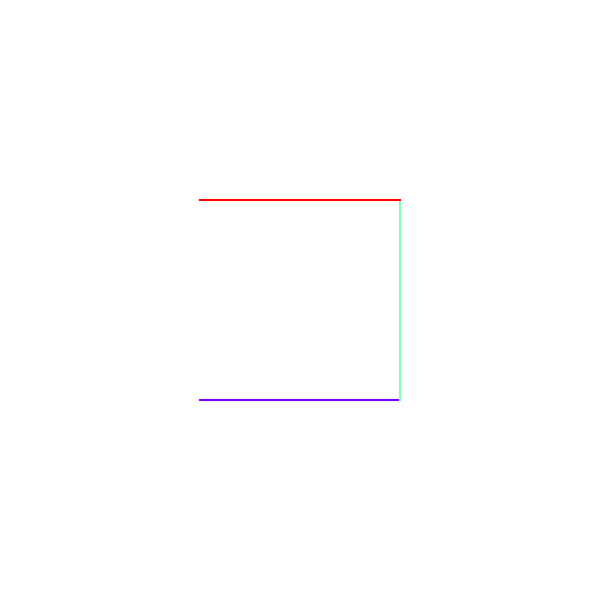
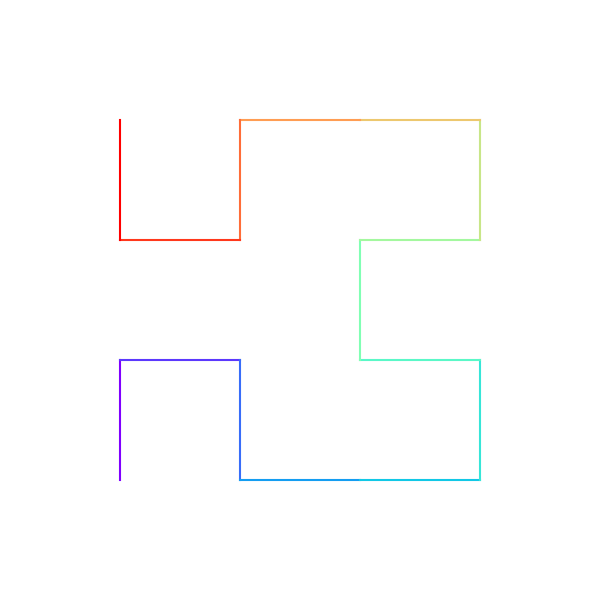




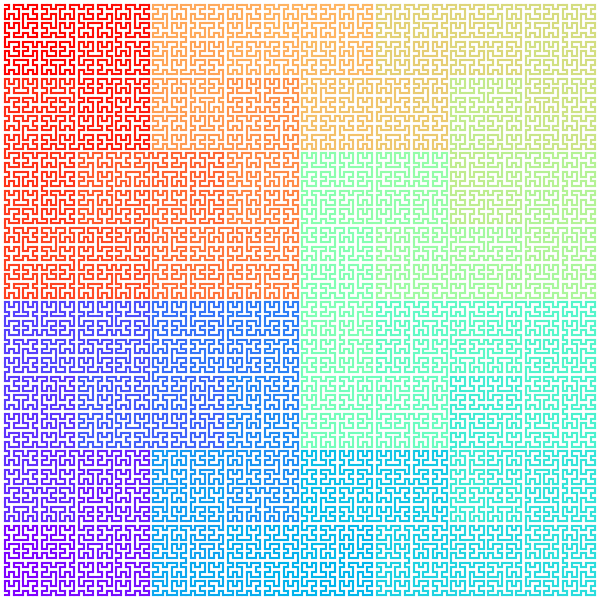
จากนั้นลองเอามาทำเป็นภาพเคลื่อนไหวดู โดยใส่ฉากหลังไว้ แล้วค่อยๆวาดเส้นให้เห็นพื้นที่ที่ถูกวาดไปเรื่อยๆ
import imageio as imo
phap = imo.imread('remram.jpg')
n = 5
X = np.array(hilbert(n,1))
for i in range(2,len(X)+1):
fig = plt.figure(figsize=[6.4,6.4],facecolor='k')
plt.axes([0,0,1,1],aspect=1,xlim=[-0.5,2**n-0.5],ylim=[-0.5,2**n-0.5])
plt.plot(X[:i,0],X[:i,1],'w',lw=13)
plt.axis('off')
fig.canvas.draw()
ar = np.array(fig.canvas.renderer._renderer)[:,:,:3]/255.
ar *= phap
imo.imsave('remram/rr%04d.jpg'%i,ar)
plt.close()ภาพฉากหลังเอามาจาก https://www.pixiv.net/artworks/67137373

ผลออกมาก็จะได้ภาพเป็นลำดับขั้นตอนออกมา 1023 ภาพ และนี่เป็นหนึ่งในนั้น

จากนั้นก็เอาภาพที่ได้ทั้งหมดมาประกอบเป็นวีดีโออีกที ผลที่ได้ลงเอาไว้ใน facebook เข้าไปดูได้ >> https://www.facebook.com/ikamiso/videos/1746538728776466
นอกจากนี้ยังได้ลองเอามาสร้างเป็นแบบจำลองสามมิติของทางวงกดขึ้นมาในมายาด้วย ตัวโค้ดได้แจกไว้ใน https://github.com/phyblas/yamimayapython/blob/master/tham_khong_tangtang/wongkot/wongkot_hilbert.py
กลายเป็นเส้นทางที่ต้องเดินคดเคี้ยวต่อเนื่องตลอดตั้งแต่ทางเข้าไปจนถึงทางออกแบบนี้

-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib