maya python เบื้องต้น บทที่ ๓๒: การสร้างพื้นผิว NURBS
เขียนเมื่อ 2016/03/11 23:23
แก้ไขล่าสุด 2024/02/20 07:16
ในบทที่แล้วได้ แนะนำสิ่งที่เรียกว่า NURBS (Non-Uniform Rational Basis Spline) ไปแล้ว โดยได้พูดถึงเส้นโค้ง NURBS ไปก่อน ส่วนในบทนี้จะพูดถึงพื้นผิว NURBS
คำสั่งสร้างพื้นผิว NURBS นั้นมีอยู่หลากหลายเช่นเดียวกับการสร้างโพลิกอน สามารถเริ่มสร้างจากรูปทรงต่างๆได้หลายชนิด
ในจำนวนนั้นที่ดูเป็นพื้นฐานที่สุดก็คือระนาบสี่เหลี่ยม ซึ่งสร้างได้ง่ายโดยฟังก์ชัน nurbsPlane()
ลองสร้างขึ้นมาดูเลย
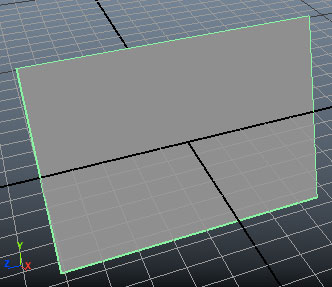
จะเห็นว่าคล้ายกับระนาบโพลิกอน สามารถกำหนดขนาดด้านได้ด้วยแฟล็ก เพียงแต่ว่าต่างกันที่ว่ากำหนดแค่ด้านแนวนอนด้วยแฟล็ก w (width) ส่วนอีกด้านใช้แฟล็ก lr (lengthRatio) ซึ่งคือค่าสัดส่วนระหว่างด้านแนวตั้งกับแนวนอน ในที่นี้เป็น 0.8 จึงสูง 0.8*10 = 8
โครงสร้างผิว NURBS นั้นประกอบขึ้นจากเส้น NURBS หลายเส้นมาสานกันเหมือนการนำเส้นใยมาทอเป็นผ้า ดังนั้นรูปร่างของผิว NURBS จะถูกควบคุมโดยเส้นต่างๆที่มาสานทอ
อนึ่ง ในทางกราฟิกแล้ว อักษร u กับ v มักถูกใช้แทนพิกัดของพื้นผิวสองมิติ โดย u เป็นแนวนอน v เป็นแนวตั้ง เรียกว่าเป็นพิกัด uv (ซึ่งไม่มีความเกี่ยวข้องกับรังสี uv แต่อย่างใด)
การเข้าถึงจุด cv ของผิว NURBS ทำได้โดยพิมพ์ชื่อวัตถุแล้วตามด้วย .cv[u][v] โดย u และ v ในที่นี้คือพิกัดในแนวตั้งและแนวนอน พิกัดแบ่งเป็นสองมิติชัดเจนผิดกับของโพลิกอนที่นับเรียงไปเรื่อยๆ
หากใส่เป็นดอกจัน * ไปจะเป็นการเลือกทั้งหมด
ลอง
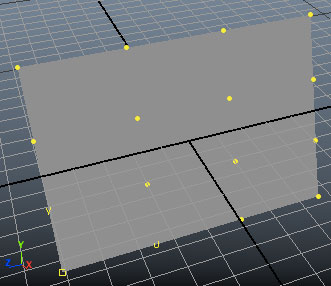
ก็จะเห็นจุด cv ทั้งหมดของผิวนี้ ซึ่งมีทั้งหมดแนวตั้งและแนวนอนอย่างละ ๔ จุด รวมเป็น ๑๖ จุด โดยไล่จาก 0 ไปถึง 3 ในแต่ละแนว
จำนวนจุด cv จะขึ้นอยู่กับดีกรีบวกกับจำนวนช่วงแบ่ง โดยแต่ละแนวคิดแยกกัน ค่าตั้งต้นนั้นดีกรีเป็น 3 และช่วงแบ่งเป็น 1 คือไม่มีการแบ่งส่วนย่อย ดังนั้นจำนวนจุด cv จึงเป็น 3+1=4
ดีกรีสามารถกำหนดได้โดยแฟล็ก d (degree) ถ้าไม่ใส่ก็จะเป็น 3 ซึ่งเป็นค่าที่กำลังดีอยู่แล้วจึงมักไม่จำเป็นต้องปรับ
ส่วนจำนวนช่วงแบ่งกำหนดโดยแฟล็ก u (patchesU) ในแนวนอน และ v (patchesV) ในแนวตั้ง
ลองกำหนดแฟล็ก u กับ v ดู

จะเห็นว่าผิวถูกแบ่งออกเป็น 4x4=16 ส่วน และมี cv 7x7=49 จุด
จุด cv เราสามารถเลื่อนเพื่อปรับรูปร่างของผิวได้ตามต้องการ เช่นลองดึงจุดตรงกลางออกไปดู

จะเห็นว่าต่างจากโพลิกอนตรงที่ผิวที่ถูกดึงออกมานั้นจะมีลักษณะโค้ง ไม่ได้เป็นเหลี่ยม ทำให้ผิว NURBS เหมาะกับการทำงานกับวัตถุที่เป็นเส้นโค้งมากกว่า
นอกจากนี้ยังมี แฟล็ก ax (axis) สำหรับกำหนดทิศว่าผิวจะหันไปทางไหน โดยถ้าไม่กำหนดผิวจะหันโดยมีแนว u เป็นแนวนอนตามระนาบ z และผิว v เป็นแนวตั้งตามแกน y
สรุปแฟล็กของระนาบ NURBS ที่พูดถึงไป
นอกจากนี้ยังมีคำสั่งสร้างผิว NURBS อีกหลายชนิด คล้ายโพลิกอน
nurbsCube() ทรงสี่เหลี่ยม
cylinder() ทรงกระบอก
sphere() ทรงกลม
cone() ทรงกรวย
torus() ทรงโดนัท
เพียงแต่ว่าจะต่างจากโพลิกอนพอสมควร
เช่น ลองสร้างทรงสี่เหลี่ยม จะเห็นว่าได้แผ่นสี่เหลี่ยมออกมา ๖ ชิ้น วัตถุที่ได้ไม่ได้เป็นชิ้นเดียวต่อกัน
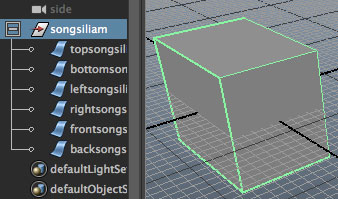
นั่นเป็นเพราะว่า NURBS นั้นมักใช้สร้างผิวโค้ง ถ้าเจอวัตถุที่มีการหักมุมแบบนี้ใช้แยกเป็นคนละผิวไปเลยจะง่ายกว่า
สำหรับทรงสี่เหลี่ยม
ส่วน u v ax จะมีเหมือนกับของระนาบ
ส่วนทรงกระบอกนั้นจะมีคุณสมบัติบางอย่างที่น่าสนใจคือสามารถทำทรงที่ไม่ได้ห่อเต็มวงได้ ลอง
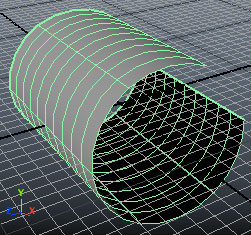
แฟล็ก ssw (startSweep) และ esw (endSweep) นี้คือมุมกวาดเริ่มต้นและมุมกวาดปลาย โดยปกติถ้าเริ่มที่ 0 และจบที่ 360 ก็จะเป็นวงกลมพอดี แต่สามารถทำให้แหว่งได้ด้วยการกำหนดมุมกวาด
ทรงกลมก็สามารถทำเป็นรูปทรงแหว่งได้เช่นกัน แบบนี้จึงสามารถสร้างแพ็กแมนขึ้นได้ง่ายๆ
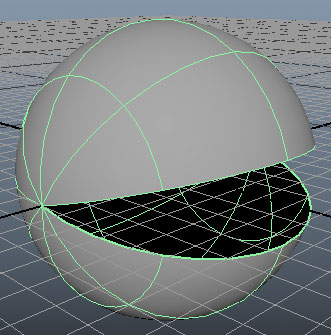
หากลองมาดูรายละเอียดโครงสร้างของแพ็กแมนตัวนี้ก็จะเห็นว่าแม้จะดูกลมๆแบบนี้ แต่ก็เกิดมาจากการที่เอาแผ่นสี่เหลี่ยมมาดัดให้โค้งแบบนี้นั่นเอง โครงสร้างของผิว NURBS มีพื้นฐานมาจากสี่เหลี่ยม ซึ่งต่างจากโพลิกอนที่อาจเป็นสามเหลี่ยมหรือสี่เหลี่ยมหรือหลายเหลี่ยมมาต่อกัน
นอกจากนี้ก็มี NURBS ทรงกรวย cone() กับทรงโดนัท torus() ซึ่งก็มีคุณสมบัติในทำนองเดียวกัน
ข้อดีของพื้นผิว NURBS อีกอย่างก็คือพื้นผิว NURBS สามารถแปลงเป็นโพลิกอนเมื่อไหร่ก็ได้ แต่โพลิกอนจะไม่สามารถแปลงเป็นพื้นผิว NURBSได้ ดังนั้นหากคิดว่ารูปทรงไหนใช้พื้นผิว NURBS แล้วสร้างง่ายกว่าก็อาจเริ่มสร้างเป็นพื้นผิว NURBS แล้วค่อยแปลงเป็นโพลิกอนทีหลังก็ได้
ในความเป็นจริงแล้วปกติพื้นผิว NURBS เวลาที่เรนเดอร์จะต้องถูกแปลงเป็นโพลิกอนโดยอัตโนมัติ
คำสั่งที่ใช้แปลงพื้นผิว NURBS เป็นโพลิกอนคือ nurbsToPoly()
การแปลงนั้นมีอยู่ ๓ โหมดให้เลือกด้วยกัน ซึ่งกำหนดโดยแฟล็ก f (format)
f=0 แปลงโดยกำหนดจำนวนโพลิกอนตายตัว
f=1 แปลงแบบปรับให้ตามความเหมาะสม
f=2 แปลงโดยปรับตาม cv
และต้องเลือกรูปแบบว่าจะแปลงเป็นโพลิกอนสามเหลี่ยมหรือสี่เหลี่ยมโดยแฟล็ก pt (polygonType)
pt=0 สามเหลี่ยม
pt=1 สี่เหลี่ยม
กรณีที่เลือก f=0 คือกำหนดจำนวนโพลิกอนตายตัวนั้นจะต้องกำหนดจำนวนโพลิกอนโดยใช้แฟล็ก pc (polygonCount) เวลาที่แปลงโปรแกรมจะพยายามแปลงให้ได้จำนวนโพลิกอนใกล้เคียงกับที่กำหนดมาก ที่สุด
ลองสร้างผิว NURBS ขึ้นมาแล้วสร้างใช้เป็นแบบโพลิกอนหลายๆอันเทียบกันดู

ภาพตรงกลางคือ NURBS ต้นแบบ ส่วนสี่อันรอบทิศคือโพลิกอนที่สร้างขึ้นโดยกำหนดแฟล็กต่างๆกัน
เมื่อใช้คำสั่งนี้เสร็จแล้ว NURBS ต้นฉบับนั้นจะยังไม่ได้หายไปไหน ถ้าไม่ต้องการแล้วก็ลบทิ้งได้
หากไม่ลบ NURBS ต้นฉบับทิ้งเวลาที่ NURBS นี้มีการเปลี่ยนแปลงหรือเคลื่อนไหวไปโพลิกอนที่สร้างขึ้นมาใหม่นี้ก็จะมีการ เปลี่ยนแปลงไปด้วย
แต่หากต้องการเก็บ NURBS ไว้โดยไม่มีผลกระทบต่อโพลิกอนอีกต่อไปก็ทำได้โดยใส่แฟล็ก ch (constructionHistory) เป็น ch=0 ซึ่งเป็นการลบประวัติศาสตร์ทิ้ง ไม่ให้โพลิกอนจดจำไว้ว่ามันถูกสร้างขึ้นมาจากไหน
ถ้ามีรายละเอียดมากก็ยิ่งควรใช้จำนวนโพลิกอนมาก โพลิกอนน้อยเกินจะทำให้รายละเอียดหายไป
ลองดูตัวอย่าง สร้างวัตถุ NURBS ที่มีลักษณะคล้ายถ้วยที่แหว่งไปเสี้ยวหนึ่งแล้วแปลงเป็นโพลิกอนโดยกำหนดจำนวนโพลิกอนต่างกัน

จากหน้าไปหลังคือจำนวนโพลิกอน 2560 ลดลงทีละ 2 เท่าไปจนเหลือแค่ 80 ส่วนอันไกลสุดคือ NURBS ต้นแบบ
นอกจาก จะใช้คำสั่ง nurbsToPoly() แล้ว ยังมีอีกวิธีที่จะสร้างโพลิกอนขึ้นจากผิว NURBS นั่นคือตอนที่ใช้ฟังก์ชันต่างๆสร้างผิว NURBS ขึ้นมานั้นให้เติมแฟล็ก po (polygon) เป็น po=1 แบบนี้แล้ววัตถุที่ถูกสร้างขึ้นจะเปลี่ยนเป็นโพลิกอนทันที
เพียงแต่ว่าจำการกำหนดว่าจะเปลี่ยนเป็นโพลิกอนในรูปแบบไหนนั้นจำเป็นต้องกำหนดโดยฟังก์ชัน nurbsToPolygonsPref()
แฟล็กต่างๆของฟังก์ชันนี้จะตรงกับฟังก์ชัน nurbsToPoly() เพียงแต่ว่าฟังก์ชันนี้ไม่ได้ทำการเปลี่ยนเป็นโพลิกอนทันทีแต่มีไว้กำหนดรูป แบบของการแปลงโพลิกอนเวลาใช้แฟล็ก po เท่านั้น
ตัวอย่างการใช้ เช่นการสร้างส่วนของทรงกลม ซึ่งเป็นสิ่งที่ใช้โพลิกอนสร้างยาก แต่สำหรับ NURBS แล้วสร้างได้ง่าย ดังนั้นเราใช้ประโยชน์จากตรงนี้สร้างโพลิกอนของส่วนของทรงกลมได้ทันที
ในนี้เป็นการสร้างส่วนของทรงกลมมาทั้งหมด ๑๒ อัน โดยจำนวนโพลิกอนแปรผันตั้งแต่ 2 ไปจนถึง 4096

อ้างอิง
คำสั่งสร้างพื้นผิว NURBS นั้นมีอยู่หลากหลายเช่นเดียวกับการสร้างโพลิกอน สามารถเริ่มสร้างจากรูปทรงต่างๆได้หลายชนิด
ในจำนวนนั้นที่ดูเป็นพื้นฐานที่สุดก็คือระนาบสี่เหลี่ยม ซึ่งสร้างได้ง่ายโดยฟังก์ชัน nurbsPlane()
ลองสร้างขึ้นมาดูเลย
mc.nurbsPlane(w=10,lr=0.8,n='np01')

จะเห็นว่าคล้ายกับระนาบโพลิกอน สามารถกำหนดขนาดด้านได้ด้วยแฟล็ก เพียงแต่ว่าต่างกันที่ว่ากำหนดแค่ด้านแนวนอนด้วยแฟล็ก w (width) ส่วนอีกด้านใช้แฟล็ก lr (lengthRatio) ซึ่งคือค่าสัดส่วนระหว่างด้านแนวตั้งกับแนวนอน ในที่นี้เป็น 0.8 จึงสูง 0.8*10 = 8
โครงสร้างผิว NURBS นั้นประกอบขึ้นจากเส้น NURBS หลายเส้นมาสานกันเหมือนการนำเส้นใยมาทอเป็นผ้า ดังนั้นรูปร่างของผิว NURBS จะถูกควบคุมโดยเส้นต่างๆที่มาสานทอ
อนึ่ง ในทางกราฟิกแล้ว อักษร u กับ v มักถูกใช้แทนพิกัดของพื้นผิวสองมิติ โดย u เป็นแนวนอน v เป็นแนวตั้ง เรียกว่าเป็นพิกัด uv (ซึ่งไม่มีความเกี่ยวข้องกับรังสี uv แต่อย่างใด)
การเข้าถึงจุด cv ของผิว NURBS ทำได้โดยพิมพ์ชื่อวัตถุแล้วตามด้วย .cv[u][v] โดย u และ v ในที่นี้คือพิกัดในแนวตั้งและแนวนอน พิกัดแบ่งเป็นสองมิติชัดเจนผิดกับของโพลิกอนที่นับเรียงไปเรื่อยๆ
หากใส่เป็นดอกจัน * ไปจะเป็นการเลือกทั้งหมด
ลอง
mc.select('np01.cv[*][*]')

ก็จะเห็นจุด cv ทั้งหมดของผิวนี้ ซึ่งมีทั้งหมดแนวตั้งและแนวนอนอย่างละ ๔ จุด รวมเป็น ๑๖ จุด โดยไล่จาก 0 ไปถึง 3 ในแต่ละแนว
จำนวนจุด cv จะขึ้นอยู่กับดีกรีบวกกับจำนวนช่วงแบ่ง โดยแต่ละแนวคิดแยกกัน ค่าตั้งต้นนั้นดีกรีเป็น 3 และช่วงแบ่งเป็น 1 คือไม่มีการแบ่งส่วนย่อย ดังนั้นจำนวนจุด cv จึงเป็น 3+1=4
ดีกรีสามารถกำหนดได้โดยแฟล็ก d (degree) ถ้าไม่ใส่ก็จะเป็น 3 ซึ่งเป็นค่าที่กำลังดีอยู่แล้วจึงมักไม่จำเป็นต้องปรับ
ส่วนจำนวนช่วงแบ่งกำหนดโดยแฟล็ก u (patchesU) ในแนวนอน และ v (patchesV) ในแนวตั้ง
ลองกำหนดแฟล็ก u กับ v ดู
mc.nurbsPlane(w=16,lr=1,u=4,v=4,n='np02')
mc.select('np02.cv[*][*]')
mc.select('np02.cv[*][*]')

จะเห็นว่าผิวถูกแบ่งออกเป็น 4x4=16 ส่วน และมี cv 7x7=49 จุด
จุด cv เราสามารถเลื่อนเพื่อปรับรูปร่างของผิวได้ตามต้องการ เช่นลองดึงจุดตรงกลางออกไปดู
mc.move(12,0,0,'np02.cv[3][3]')

จะเห็นว่าต่างจากโพลิกอนตรงที่ผิวที่ถูกดึงออกมานั้นจะมีลักษณะโค้ง ไม่ได้เป็นเหลี่ยม ทำให้ผิว NURBS เหมาะกับการทำงานกับวัตถุที่เป็นเส้นโค้งมากกว่า
นอกจากนี้ยังมี แฟล็ก ax (axis) สำหรับกำหนดทิศว่าผิวจะหันไปทางไหน โดยถ้าไม่กำหนดผิวจะหันโดยมีแนว u เป็นแนวนอนตามระนาบ z และผิว v เป็นแนวตั้งตามแกน y
สรุปแฟล็กของระนาบ NURBS ที่พูดถึงไป
| w | (width) | ความกว้าง | ค่าตั้งต้นคือ 1 |
| lr | (lengthRatio) | สัดส่วนระหว่างด้าน แนวตั้งต่อแนวนอน | ค่าตั้งต้นคือ 1 |
| d | (degree) | ดีกรี | ค่าตั้งต้นคือ 3 |
| u | (patchesU) | จำนวนส่วนแบ่งแนวนอน | ค่าตั้งต้นคือ 1 |
| v | (patchesV) | จำนวนส่วนแบ่งแนวตั้ง | ค่าตั้งต้นคือ 1 |
| ax | (axis) | แกนหัน | ค่าตั้งต้นคือ 1,0,0 |
นอกจากนี้ยังมีคำสั่งสร้างผิว NURBS อีกหลายชนิด คล้ายโพลิกอน
nurbsCube() ทรงสี่เหลี่ยม
cylinder() ทรงกระบอก
sphere() ทรงกลม
cone() ทรงกรวย
torus() ทรงโดนัท
เพียงแต่ว่าจะต่างจากโพลิกอนพอสมควร
เช่น ลองสร้างทรงสี่เหลี่ยม จะเห็นว่าได้แผ่นสี่เหลี่ยมออกมา ๖ ชิ้น วัตถุที่ได้ไม่ได้เป็นชิ้นเดียวต่อกัน
mc.nurbsCube(w=10,lr=1.2,hr=1.5,n='songsiliam')

นั่นเป็นเพราะว่า NURBS นั้นมักใช้สร้างผิวโค้ง ถ้าเจอวัตถุที่มีการหักมุมแบบนี้ใช้แยกเป็นคนละผิวไปเลยจะง่ายกว่า
สำหรับทรงสี่เหลี่ยม
| w | (width) | ความยาวด้านกว้าง | ค่าตั้งต้นคือ 1 |
| lr | (lengthRatio) | สัดส่วนด้านยาวต่อด้านกว้าง | ค่าตั้งต้นคือ 1 |
| hr | (heightRatio) | สัดส่วนด้านสูงต่อด้านกว้าง | ค่าตั้งต้นคือ 1 |
ส่วนทรงกระบอกนั้นจะมีคุณสมบัติบางอย่างที่น่าสนใจคือสามารถทำทรงที่ไม่ได้ห่อเต็มวงได้ ลอง
mc.cylinder(r=5,hr=3,nsp=10,s=5,ssw=0,esw=300)

แฟล็ก ssw (startSweep) และ esw (endSweep) นี้คือมุมกวาดเริ่มต้นและมุมกวาดปลาย โดยปกติถ้าเริ่มที่ 0 และจบที่ 360 ก็จะเป็นวงกลมพอดี แต่สามารถทำให้แหว่งได้ด้วยการกำหนดมุมกวาด
| r | (radius) | รัศมี | ค่าตั้งต้นคือ 1 |
| hr | (heightRatio) | สัดส่วนความสูงต่อรัศมี | ค่าตั้งต้นคือ 2 |
| nsp | (spans) | จำนวนส่วนแบ่งแนว u (ตามความยาว) | ค่าตั้งต้นคือ 1 |
| s | (sections) | จำนวนส่วนแบ่งแนว v (วนรอบวง) | ค่าตั้งต้นคือ 8 |
| ssw | (startSweep) | มุมกวาดเริ่มต้น | ค่าตั้งต้นคือ 0 |
| esw | (endSweep) | มุมกวาดปลาย | ค่าตั้งต้นคือ 360 (2π) |
ทรงกลมก็สามารถทำเป็นรูปทรงแหว่งได้เช่นกัน แบบนี้จึงสามารถสร้างแพ็กแมนขึ้นได้ง่ายๆ
mc.sphere(r=5,ssw=15,esw=345,n='pacman')

หากลองมาดูรายละเอียดโครงสร้างของแพ็กแมนตัวนี้ก็จะเห็นว่าแม้จะดูกลมๆแบบนี้ แต่ก็เกิดมาจากการที่เอาแผ่นสี่เหลี่ยมมาดัดให้โค้งแบบนี้นั่นเอง โครงสร้างของผิว NURBS มีพื้นฐานมาจากสี่เหลี่ยม ซึ่งต่างจากโพลิกอนที่อาจเป็นสามเหลี่ยมหรือสี่เหลี่ยมหรือหลายเหลี่ยมมาต่อกัน
นอกจากนี้ก็มี NURBS ทรงกรวย cone() กับทรงโดนัท torus() ซึ่งก็มีคุณสมบัติในทำนองเดียวกัน
ข้อดีของพื้นผิว NURBS อีกอย่างก็คือพื้นผิว NURBS สามารถแปลงเป็นโพลิกอนเมื่อไหร่ก็ได้ แต่โพลิกอนจะไม่สามารถแปลงเป็นพื้นผิว NURBSได้ ดังนั้นหากคิดว่ารูปทรงไหนใช้พื้นผิว NURBS แล้วสร้างง่ายกว่าก็อาจเริ่มสร้างเป็นพื้นผิว NURBS แล้วค่อยแปลงเป็นโพลิกอนทีหลังก็ได้
ในความเป็นจริงแล้วปกติพื้นผิว NURBS เวลาที่เรนเดอร์จะต้องถูกแปลงเป็นโพลิกอนโดยอัตโนมัติ
คำสั่งที่ใช้แปลงพื้นผิว NURBS เป็นโพลิกอนคือ nurbsToPoly()
การแปลงนั้นมีอยู่ ๓ โหมดให้เลือกด้วยกัน ซึ่งกำหนดโดยแฟล็ก f (format)
f=0 แปลงโดยกำหนดจำนวนโพลิกอนตายตัว
f=1 แปลงแบบปรับให้ตามความเหมาะสม
f=2 แปลงโดยปรับตาม cv
และต้องเลือกรูปแบบว่าจะแปลงเป็นโพลิกอนสามเหลี่ยมหรือสี่เหลี่ยมโดยแฟล็ก pt (polygonType)
pt=0 สามเหลี่ยม
pt=1 สี่เหลี่ยม
กรณีที่เลือก f=0 คือกำหนดจำนวนโพลิกอนตายตัวนั้นจะต้องกำหนดจำนวนโพลิกอนโดยใช้แฟล็ก pc (polygonCount) เวลาที่แปลงโปรแกรมจะพยายามแปลงให้ได้จำนวนโพลิกอนใกล้เคียงกับที่กำหนดมาก ที่สุด
ลองสร้างผิว NURBS ขึ้นมาแล้วสร้างใช้เป็นแบบโพลิกอนหลายๆอันเทียบกันดู
p = mc.nurbsPlane(w=10,ax=[0,1,0],u=2,v=3)[0]
mc.move(0,10,0,p+'.cv[2][2]',r=1)
mc.nurbsToPoly(p,f=0,pt=1,pc=30)
mc.move(0,0,-10)
mc.nurbsToPoly(p,f=0,pt=0,pc=30)
mc.move(0,0,10)
mc.nurbsToPoly(p,f=0,pt=1,pc=300)
mc.move(-10,0,0)
mc.nurbsToPoly(p,f=2,pt=0)
mc.move(10,0,0)
mc.move(0,10,0,p+'.cv[2][2]',r=1)
mc.nurbsToPoly(p,f=0,pt=1,pc=30)
mc.move(0,0,-10)
mc.nurbsToPoly(p,f=0,pt=0,pc=30)
mc.move(0,0,10)
mc.nurbsToPoly(p,f=0,pt=1,pc=300)
mc.move(-10,0,0)
mc.nurbsToPoly(p,f=2,pt=0)
mc.move(10,0,0)

ภาพตรงกลางคือ NURBS ต้นแบบ ส่วนสี่อันรอบทิศคือโพลิกอนที่สร้างขึ้นโดยกำหนดแฟล็กต่างๆกัน
เมื่อใช้คำสั่งนี้เสร็จแล้ว NURBS ต้นฉบับนั้นจะยังไม่ได้หายไปไหน ถ้าไม่ต้องการแล้วก็ลบทิ้งได้
หากไม่ลบ NURBS ต้นฉบับทิ้งเวลาที่ NURBS นี้มีการเปลี่ยนแปลงหรือเคลื่อนไหวไปโพลิกอนที่สร้างขึ้นมาใหม่นี้ก็จะมีการ เปลี่ยนแปลงไปด้วย
แต่หากต้องการเก็บ NURBS ไว้โดยไม่มีผลกระทบต่อโพลิกอนอีกต่อไปก็ทำได้โดยใส่แฟล็ก ch (constructionHistory) เป็น ch=0 ซึ่งเป็นการลบประวัติศาสตร์ทิ้ง ไม่ให้โพลิกอนจดจำไว้ว่ามันถูกสร้างขึ้นมาจากไหน
ถ้ามีรายละเอียดมากก็ยิ่งควรใช้จำนวนโพลิกอนมาก โพลิกอนน้อยเกินจะทำให้รายละเอียดหายไป
ลองดูตัวอย่าง สร้างวัตถุ NURBS ที่มีลักษณะคล้ายถ้วยที่แหว่งไปเสี้ยวหนึ่งแล้วแปลงเป็นโพลิกอนโดยกำหนดจำนวนโพลิกอนต่างกัน
p = mc.cylinder(r=1,hr=3,nsp=10,s=18,ssw=0,esw=330,ax=[0,1,0])[0]
mc.scale(3,3,3,
[p+'.cv[%d][*]'%i for i in range(2,11,2)]+
[p+'.cv[*][%d]'%i for i in range(2,19,2)])
for i in range(1,7):
mc.nurbsToPoly(p,f=0,pc=40*2**i,pt=0)
mc.move(0,0,6*i)
mc.scale(3,3,3,
[p+'.cv[%d][*]'%i for i in range(2,11,2)]+
[p+'.cv[*][%d]'%i for i in range(2,19,2)])
for i in range(1,7):
mc.nurbsToPoly(p,f=0,pc=40*2**i,pt=0)
mc.move(0,0,6*i)

จากหน้าไปหลังคือจำนวนโพลิกอน 2560 ลดลงทีละ 2 เท่าไปจนเหลือแค่ 80 ส่วนอันไกลสุดคือ NURBS ต้นแบบ
นอกจาก จะใช้คำสั่ง nurbsToPoly() แล้ว ยังมีอีกวิธีที่จะสร้างโพลิกอนขึ้นจากผิว NURBS นั่นคือตอนที่ใช้ฟังก์ชันต่างๆสร้างผิว NURBS ขึ้นมานั้นให้เติมแฟล็ก po (polygon) เป็น po=1 แบบนี้แล้ววัตถุที่ถูกสร้างขึ้นจะเปลี่ยนเป็นโพลิกอนทันที
เพียงแต่ว่าจำการกำหนดว่าจะเปลี่ยนเป็นโพลิกอนในรูปแบบไหนนั้นจำเป็นต้องกำหนดโดยฟังก์ชัน nurbsToPolygonsPref()
แฟล็กต่างๆของฟังก์ชันนี้จะตรงกับฟังก์ชัน nurbsToPoly() เพียงแต่ว่าฟังก์ชันนี้ไม่ได้ทำการเปลี่ยนเป็นโพลิกอนทันทีแต่มีไว้กำหนดรูป แบบของการแปลงโพลิกอนเวลาใช้แฟล็ก po เท่านั้น
ตัวอย่างการใช้ เช่นการสร้างส่วนของทรงกลม ซึ่งเป็นสิ่งที่ใช้โพลิกอนสร้างยาก แต่สำหรับ NURBS แล้วสร้างได้ง่าย ดังนั้นเราใช้ประโยชน์จากตรงนี้สร้างโพลิกอนของส่วนของทรงกลมได้ทันที
for i in range(1,13):
mc.nurbsToPolygonsPref(f=0,pc=2**i,pt=1)
p = mc.sphere(r=5,ssw=i*30,esw=i*30+15,po=1)
mc.nurbsToPolygonsPref(f=0,pc=2**i,pt=1)
p = mc.sphere(r=5,ssw=i*30,esw=i*30+15,po=1)
ในนี้เป็นการสร้างส่วนของทรงกลมมาทั้งหมด ๑๒ อัน โดยจำนวนโพลิกอนแปรผันตั้งแต่ 2 ไปจนถึง 4096

อ้างอิง
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/nurbsPlane.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/nurbsCube.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/cylinder.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/sphere.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/cone.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/torus.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/nurbsToPoly.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/nurbsToPolygonsPref.html
https://knowledge.autodesk.com/ja/support/maya/learn-explore/caas/CloudHelp/cloudhelp/2016/JPN/Maya/files/GUID-DC38BD08-A411-4403-8C59-104337673266-htm.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/nurbsCube.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/cylinder.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/sphere.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/cone.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/torus.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/nurbsToPoly.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/nurbsToPolygonsPref.html
https://knowledge.autodesk.com/ja/support/maya/learn-explore/caas/CloudHelp/cloudhelp/2016/JPN/Maya/files/GUID-DC38BD08-A411-4403-8C59-104337673266-htm.html