numpy & matplotlib เบื้องต้น บทที่ ๒๕: การปรับแต่งคัลเลอร์แม็ป
เขียนเมื่อ 2016/06/12 10:25
แก้ไขล่าสุด 2021/09/28 16:42
ในบทที่แล้วได้แนะนำสิ่งที่เรียกว่าคัลเลอร์แม็ปและการใช้งานเพื่อสร้างแผนภาพไล่สีไปแล้ว
ในบทนี้จะเป็นเนื้อเพิ่มเติมเสริมจากบทที่แล้ว โดยจะเพิ่มทางเลือกในการปรับแต่งอะไรต่างๆให้มากขึ้น
การปรับขอบเขตของแถบสี
ตาม ที่ได้กล่าวไปในบทที่แล้วว่าฟังก์ชันคัลเลอร์แม็ปนั้นจะรับค่าตัวเลขในช่วง 0 ถึง 1 มาแล้วแปลงเป็นค่าแม่สีทั้ง ๓ (และยังมีตัวที่ ๔ คือค่าความโปร่งใสซึ่งในที่นี้จะไม่พูดถึง)
เช่นลองดูคัลเลอร์แม็ป ที่ชื่อ rainbow ซึ่งไล่สีเป็นสีรุ้ง ลองทดสอบค่าสีโดยการใส่ค่าตั้งแต่ 0 ถึง 1 ลงในฟังก์ชัน get_cmap('rainbow')()
ผลลัพธ์
จะเห็นว่าค่าสีที่ 0 คือสีม่วง และที่ 1 คือสีแดง
แม้ว่าคัลเลอร์แม็ปจะมีค่าเปลี่ยนแปลงอยู่แค่ในช่วง 0 ถึง 1 แต่เวลาที่เราใช้งานคัลเลอร์แม็ปจริงๆนั้นเราไม่จำเป็นต้องมาคอยเปลี่ยน ค่าที่จะใช้เป็นค่าสีให้อยู่ในช่วง 0 ถึง 1 นั่นเป็นเพราะโดยปกติเวลาที่นำคัลเลอร์แม็ปมาใช้งานเช่นใส่ลงในแผนภาพไล่สี สีจะถูกไล่จากค่าต่ำสุดไปยังค่าสูงสุด
เช่นลองดูตัวอย่างนี้

ภาพนี้มีการไล่สีตั้งแต่ค่าต่ำสุดคือ -5 เป็นสีม่วง และค่าสูงสุดคือ 5 เป็นสีแดง กรณีนี้โปรแกรมได้ทำการแปลง -5 เป็น 0 และ 5 เป็น 1 และค่าระหว่างนั้นก็เทียบสัดส่วนกันไป การทำแบบนี้เรียกว่านอร์มาไลซ์ (normalize)
การที่สีไล่จากสูงไปจนต่ำอย่างสวยงามโดยที่เราไม่ต้องมา กำหนดค่าสูงสุดและต่ำสุดเอง แบบนี้ก็เป็นอะไรที่สะดวกดี อย่างไรก็ตามบางครั้งก็ก่อให้เกิดปัญหาอันไม่พึงประสงค์ได้เช่นกัน เช่นสมมุติว่ามีจุดประหลาดอันเดียวที่ข้อมูลห่างจากอันอื่นมันจะดึงให้ส่วน ที่เหลือไล่สีอยู่ภายในขอบเขตแคบๆทันที
ตัวอย่างเช่น
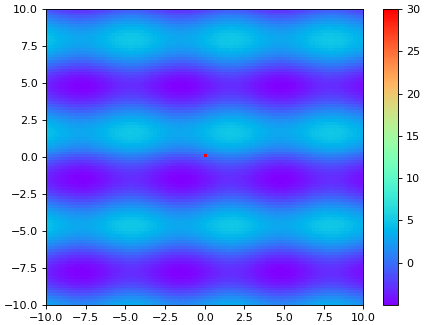
จะเห็นว่ามีจุดแดงโดดขึ้นมาเพียงจุดเดียวตรงกลาง ที่เหลือเป็นสีออกม่วงหมดเลย
ดังนั้นบางครั้งจึงอาจเป็นการดีถ้าเราจะกำหนดค่าสูงสุดและต่ำสุดตามที่ต้องการได้
เราสามารถใส่ค่า vmin และ vmax เพื่อกำหนดขอบเขตค่าต่ำสุดและสูงสุดได้ เช่น ลองแก้บรรทัด plt.pcolor เป็น
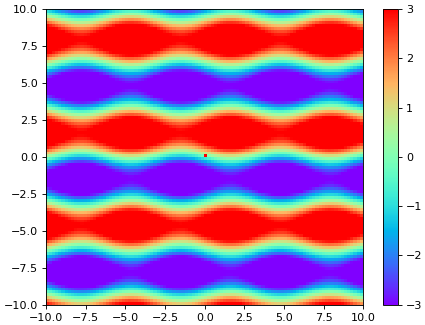
จะเห็นว่าคราวนี้สีจะมีการไล่เฉพาะในช่วงระหว่าง vmin ถึง vmax เท่านั้น ถ้าต่ำกว่า vmin หรือสูงกว่า vmax จะถือว่าเป็นสีเดียวกันหมด ไม่ว่าจะสูงกว่าหรือต่ำกว่าไปเยอะแค่ไหนก็ตาม
พอกำหนดขอบเขตตายตัวแบบนี้แล้วก็ทำให้กำจัดปัญหาการมีจุดที่มีค่าโดดขึ้นแบบผิดปกติได้ทันที
เมื่อกำหนดขอบเขต vmin และ vmax ไว้จะทำให้การนอร์มาไลซ์ทำตามช่วงขอบเขตนั้น หากเขียนเป็นสูตรคำนวณก็อาจเขียนเป็น
c = (z-vmin)/(vmax-vmin)
ออบเจ็กต์สำหรับนอร์มาไลซ์
ใน matplotlib นั้นได้จัดเตรียมออบเจ็กชนิดหนึ่งที่เอาไว้กำหนดค่าในการนอร์มาไลซ์ เราสามารถจะนำมันมาใช้เพื่อกำหนดรูปแบบการแสดงผลของแผนภาพไล่สีได้
ออบเจ็กต์ชนิดนั้นอยู่ในมอดูลย่อยหนึ่งของ matplotlib ชื่อ colors
ขอเริ่มด้วยการยกตัวอย่างการใช้แล้วจึงอธิบายทีหลัง
ตัวอย่าง พิมพ์ตามนี้จะได้ผลเหมือนกับตัวอย่างที่แล้ว
ข้อแตกต่างจากตัวอย่างที่แล้วก็คือแทนที่จะกำหนด vmin=-3,vmax=3 ตรงฟังก์ชัน plt.pcolor โดยตรงก็ไปสร้างออบเจ็กต์ mpl.colors.Normalize ขึ้น
จากนั้นจึงนำออบเจ็กต์ cnorm นี้มาใส่เป็นคีย์เวิร์ด norm ในฟังก์ชัน plt.pcolor อีกที
cnorm ที่สร้างขึ้นมานั้นที่จริงแล้วก็คือเป็นฟังก์ชันที่ทำการแปลงตัวเลขจาก -3 ถึง 3 ให้เป็น 0 ถึง 1 นั่นเอง ลองดู
จะได้
ที่จริงแล้วหากแค่ต้องการปรับขอบเขตการไล่สีเฉยๆก็แค่ใส่คีย์เวิร์ด vmin และ vmax ลงใน plt.pcolor ตามเดิมก็ได้ ไม่ต่างกัน
อย่างไรก็ตามออบเจ็กต์สำหรับนอร์มาไลซ์นั้นไม่ได้มีเพียงแค่ตัวนอร์มาไลซ์รูปแบบเชิงเส้นง่ายๆอย่างที่เห็นนี้เสมอไป แต่ยังมีตัวนอร์มาไลซ์ในรูปแบบอื่นๆด้วย
ในที่นี้จะยกตัวอย่างที่น่าจะมีโอกาสได้ใช้บ่อยมาส่วนหนึ่ง
การไล่สีแบบเรขาคณิต
บางครั้งการไล่สีแบบเป็นเชิงเส้นก็อาจไม่ทำให้เราเห็นภาพอะไรบางอย่างชัดเจนมากพอ
ตัวอย่างเช่นกราฟที่ค่าสีเปลี่ยนค่าไปตามเลขยกกำลัง
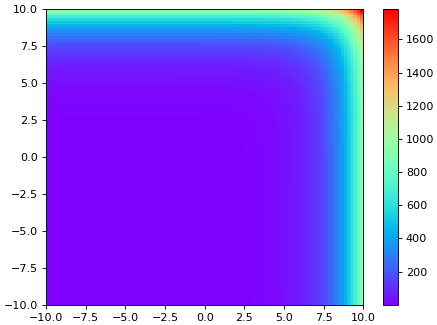
แบบนี้จะเห็นว่าสีมาเปลี่ยนตรงแถวขอบอย่างรวดเร็ว แต่หากปรับการไล่สีให้ไล่แบบเรขาคณิตแทนก็จะแสดงผลได้ดีขึ้น ซึ่งเราสามารถทำได้โดยการใช้ตัวนอร์มาไลซ์แบบเรขาคณิต
ลองดูตัวอย่างการใช้
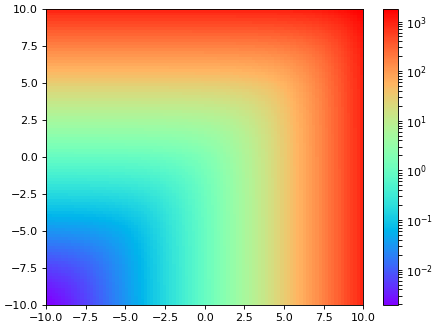
เท่านี้ก็จะเห็นว่าการไล่สีกลายเป็นแบบเรขาคณิต แถบสีทางขวาก็กลายเป็นเลขยกกำลังฐานสิบด้วย
ในที่นี้ส่วนที่เปลี่ยนแปลงไปมีแค่เราเพิ่ม mpl.colors.LogNorm() เข้ามาเป็นคีย์เวิร์ดใน plt.pcolor
mpl.colors.LogNorm นี้เป็นออบเจ็กต์นอร์มาไลซ์แบบไล่ตามยกกำลังสิบ
สามารถใส่อาร์กิวเมนต์ vmin vmax เพื่อกำหนดขอบเขตได้เช่นเดียวกับ mpl.colors.Normalize
ลองแก้ clognorm เป็น
ก็จะได้การไล่สีแค่ในช่วง 0.1 ถึง 10
ไล่สีแบบเป็นช่วงๆไม่ต่อเนื่อง
อีกรูปแบบหนึ่งที่อาจได้ใช้บ่อยก็คือการไล่สีแบบแบ่งเป็นลำดับขั้นไม่ต่อเนื่อง เป็นฟังก์ชันขั้นบันได
เราสามารถสร้างฟังก์ชันขั้นบันไดได้ด้วย mpl.colors.BoundaryNorm
ตัวอย่าง
ผลลัพธ์
ลองเอามาวาดกราฟเทียบระหว่างฟังก์ชัน y เดิมกับ y ที่ถูกแปลงค่าเป็นขั้นบันได
จะเห็นว่าฟังก์ชัน y ถูกแบ่งค่าออกเป็นช่วงๆตามค่า ค่ายิ่งมากก็ย่ิงอยู่ในขั้นที่สูง
จากที่เดิมเป็นค่าที่เพิ่มขึ้นเรื่อยๆอย่างต่อเนื่อง กลายมาเป็นว่าค่าเพิ่มขึ้นเป็นขั้นๆไม่ต่อเนื่อง ถ้าหากนี่เป็นค่าที่แทนสีก็จะได้ว่าสีเห็นสีเปลี่ยนไปเป็นช่วงๆ
กลับมาดูที่เลขที่ใส่ลงในฟังก์ชัน mpl.colors.BoundaryNorm อาร์กิวเมนต์ตัวแรกคือลิสต์หรืออาเรย์ของจุดแบ่งขีดที่ต้องการ ในที่นี้แบ่งทีละ 0.4 ไปเรื่อยๆจนถึงค่าสูงสุดคือ 4 รวมแล้วแบ่งเป็น 10 ช่วง (แต่ในลิสต์ต้องมี 11 ค่า)
ส่วนอาร์กิวเมนต์ตัวหลังคือค่าตัวเลขสูงสุด ค่าเป็นจำนวนเต็มเท่านั้น ค่าผลลัพธ์ที่ได้ออกมานั้นจะไล่ตั้งแต่ 0 ไปจนถึงตัวเลขที่กำหนดนี้ ในที่นี้กำหนดเป็น 40 ดังนั้นจึงไล่ตั้งแต่ 0 ถึง 40
โดยทั่วไปเมื่อนำมาใช้จริงจะกำหนดค่าเป็น 256 เพื่อจะนำมาใช้เป็นค่าใส่ในคัลเลอร์แม็ป
ที่จริงคัลเลอร์แม็ปนั้นนอกจากจะนอร์มาไลซ์เป็น 0 ถึง 1 แล้ว หาค่าที่ใส่ลงไปเป็นจำนวนเต็มจะเป็นการไล่ตั้งแต่ 0 ถึง 255 แทน
จะเห็นว่า plt.get_cmap('rainbow')(1) กับ plt.get_cmap('rainbow')(1.) ได้ค่าไม่เท่ากัน แต่ plt.get_cmap('rainbow')(1.) กลับเท่ากับ plt.get_cmap('rainbow')(255) แทน เพราะการใส่ค่าเป็นเลขจำนวนจริงกับจำนวนเต็มนั้นคิดต่างกัน ต้องระวังตรงนี้ด้วย
เมื่อเข้าใจแล้วคราวนี้ก็มาลองใช้ mpl.colors.BoundaryNorm กับแผนภาพไล่สีกันดูเลย ลองให้วาดภาพขึ้นมาหลายภาพ ภาพแรกเป็นการไล่สีแบบต่อเนื่อง ส่วนสามภาพที่เหลือให้วาดภาพโดยแบ่งสีเป็นขั้นๆ โดยมีจำนวนขั้นต่างออกไปเป็น 20, 10 และ 5 ตามลำดับ
แผนภาพไล่สีที่มีการแบ่งสีเป็นขั้นๆแบบนี้เรียกว่าคอนทัวร์ (contour) บางกรณีก็ช่วยให้เห็นภาพอะไรได้ชัดขึ้นกว่าการไล่สีต่อเนื่อง
อย่างไรก็ตามที่จริงนอกจากวิธีนี้แล้ว matplotlib ก็มีฟังก์ชันสำหรับสร้างคอนทัวร์โดยเฉพาะและดีกว่า ซึ่งจะกล่าวถึงในบทที่ ๒๘ ต่อไป
นอกจากรูปแบบการนอร์มาไลซ์ที่กล่าวมาข้างต้นแล้วนั้น ความจริงแล้วเรายังสามารถสร้างรูปแบบเฉพาะขึ้นมาเองได้อีกด้วย
อ้างอิง
ในบทนี้จะเป็นเนื้อเพิ่มเติมเสริมจากบทที่แล้ว โดยจะเพิ่มทางเลือกในการปรับแต่งอะไรต่างๆให้มากขึ้น
การปรับขอบเขตของแถบสี
ตาม ที่ได้กล่าวไปในบทที่แล้วว่าฟังก์ชันคัลเลอร์แม็ปนั้นจะรับค่าตัวเลขในช่วง 0 ถึง 1 มาแล้วแปลงเป็นค่าแม่สีทั้ง ๓ (และยังมีตัวที่ ๔ คือค่าความโปร่งใสซึ่งในที่นี้จะไม่พูดถึง)
เช่นลองดูคัลเลอร์แม็ป ที่ชื่อ rainbow ซึ่งไล่สีเป็นสีรุ้ง ลองทดสอบค่าสีโดยการใส่ค่าตั้งแต่ 0 ถึง 1 ลงในฟังก์ชัน get_cmap('rainbow')()
import matplotlib.pyplot as plt
for c in np.arange(0,1.1,0.1):
print('%s: %s'%(c,plt.get_cmap('rainbow')(c)))
for c in np.arange(0,1.1,0.1):
print('%s: %s'%(c,plt.get_cmap('rainbow')(c)))
ผลลัพธ์
0.0: (0.5, 0.0, 1.0, 1.0)
0.1: (0.30392156862745101, 0.30315267411304353, 0.98816547208125938, 1.0)
0.2: (0.099999999999999978, 0.58778525229247314, 0.95105651629515353, 1.0)
0.3: (0.096078431372549011, 0.80538091938883261, 0.8924005832479478, 1.0)
0.4: (0.30000000000000004, 0.95105651629515353, 0.80901699437494745, 1.0)
0.5: (0.50392156862745097, 0.99998102734872685, 0.70492554690614728, 1.0)
0.6: (0.69999999999999996, 0.95105651629515364, 0.58778525229247325, 1.0)
0.7: (0.90392156862745088, 0.80538091938883272, 0.45124405704532283, 1.0)
0.8: (1.0, 0.58778525229247325, 0.30901699437494745, 1.0)
0.9: (1.0, 0.30315267411304359, 0.15339165487868542, 1.0)
1.0: (1.0, 1.2246467991473532e-16, 6.123233995736766e-17, 1.0)
0.1: (0.30392156862745101, 0.30315267411304353, 0.98816547208125938, 1.0)
0.2: (0.099999999999999978, 0.58778525229247314, 0.95105651629515353, 1.0)
0.3: (0.096078431372549011, 0.80538091938883261, 0.8924005832479478, 1.0)
0.4: (0.30000000000000004, 0.95105651629515353, 0.80901699437494745, 1.0)
0.5: (0.50392156862745097, 0.99998102734872685, 0.70492554690614728, 1.0)
0.6: (0.69999999999999996, 0.95105651629515364, 0.58778525229247325, 1.0)
0.7: (0.90392156862745088, 0.80538091938883272, 0.45124405704532283, 1.0)
0.8: (1.0, 0.58778525229247325, 0.30901699437494745, 1.0)
0.9: (1.0, 0.30315267411304359, 0.15339165487868542, 1.0)
1.0: (1.0, 1.2246467991473532e-16, 6.123233995736766e-17, 1.0)
จะเห็นว่าค่าสีที่ 0 คือสีม่วง และที่ 1 คือสีแดง
แม้ว่าคัลเลอร์แม็ปจะมีค่าเปลี่ยนแปลงอยู่แค่ในช่วง 0 ถึง 1 แต่เวลาที่เราใช้งานคัลเลอร์แม็ปจริงๆนั้นเราไม่จำเป็นต้องมาคอยเปลี่ยน ค่าที่จะใช้เป็นค่าสีให้อยู่ในช่วง 0 ถึง 1 นั่นเป็นเพราะโดยปกติเวลาที่นำคัลเลอร์แม็ปมาใช้งานเช่นใส่ลงในแผนภาพไล่สี สีจะถูกไล่จากค่าต่ำสุดไปยังค่าสูงสุด
เช่นลองดูตัวอย่างนี้
import numpy as np
import matplotlib.pyplot as plt
x,y = np.meshgrid(np.linspace(-10,10,101),np.linspace(-10,10,101))
z = np.sin(x)+np.sin(y)*4 # ค่าสี
plt.pcolor(x,y,z,cmap='rainbow')
plt.colorbar()
plt.show()
import matplotlib.pyplot as plt
x,y = np.meshgrid(np.linspace(-10,10,101),np.linspace(-10,10,101))
z = np.sin(x)+np.sin(y)*4 # ค่าสี
plt.pcolor(x,y,z,cmap='rainbow')
plt.colorbar()
plt.show()

ภาพนี้มีการไล่สีตั้งแต่ค่าต่ำสุดคือ -5 เป็นสีม่วง และค่าสูงสุดคือ 5 เป็นสีแดง กรณีนี้โปรแกรมได้ทำการแปลง -5 เป็น 0 และ 5 เป็น 1 และค่าระหว่างนั้นก็เทียบสัดส่วนกันไป การทำแบบนี้เรียกว่านอร์มาไลซ์ (normalize)
การที่สีไล่จากสูงไปจนต่ำอย่างสวยงามโดยที่เราไม่ต้องมา กำหนดค่าสูงสุดและต่ำสุดเอง แบบนี้ก็เป็นอะไรที่สะดวกดี อย่างไรก็ตามบางครั้งก็ก่อให้เกิดปัญหาอันไม่พึงประสงค์ได้เช่นกัน เช่นสมมุติว่ามีจุดประหลาดอันเดียวที่ข้อมูลห่างจากอันอื่นมันจะดึงให้ส่วน ที่เหลือไล่สีอยู่ภายในขอบเขตแคบๆทันที
ตัวอย่างเช่น
x,y = np.meshgrid(np.linspace(-10,10,101),np.linspace(-10,10,101))
z = np.sin(x)+np.sin(y)*4
z[50,50] = 30 # เพิ่มบรรทัดนี้เข้ามา
plt.pcolor(x,y,z,cmap='rainbow')
plt.colorbar()
plt.show()
z = np.sin(x)+np.sin(y)*4
z[50,50] = 30 # เพิ่มบรรทัดนี้เข้ามา
plt.pcolor(x,y,z,cmap='rainbow')
plt.colorbar()
plt.show()

จะเห็นว่ามีจุดแดงโดดขึ้นมาเพียงจุดเดียวตรงกลาง ที่เหลือเป็นสีออกม่วงหมดเลย
ดังนั้นบางครั้งจึงอาจเป็นการดีถ้าเราจะกำหนดค่าสูงสุดและต่ำสุดตามที่ต้องการได้
เราสามารถใส่ค่า vmin และ vmax เพื่อกำหนดขอบเขตค่าต่ำสุดและสูงสุดได้ เช่น ลองแก้บรรทัด plt.pcolor เป็น
plt.pcolor(x,y,z,cmap='rainbow',vmin=-3,vmax=3)

จะเห็นว่าคราวนี้สีจะมีการไล่เฉพาะในช่วงระหว่าง vmin ถึง vmax เท่านั้น ถ้าต่ำกว่า vmin หรือสูงกว่า vmax จะถือว่าเป็นสีเดียวกันหมด ไม่ว่าจะสูงกว่าหรือต่ำกว่าไปเยอะแค่ไหนก็ตาม
พอกำหนดขอบเขตตายตัวแบบนี้แล้วก็ทำให้กำจัดปัญหาการมีจุดที่มีค่าโดดขึ้นแบบผิดปกติได้ทันที
เมื่อกำหนดขอบเขต vmin และ vmax ไว้จะทำให้การนอร์มาไลซ์ทำตามช่วงขอบเขตนั้น หากเขียนเป็นสูตรคำนวณก็อาจเขียนเป็น
c = (z-vmin)/(vmax-vmin)
ออบเจ็กต์สำหรับนอร์มาไลซ์
ใน matplotlib นั้นได้จัดเตรียมออบเจ็กชนิดหนึ่งที่เอาไว้กำหนดค่าในการนอร์มาไลซ์ เราสามารถจะนำมันมาใช้เพื่อกำหนดรูปแบบการแสดงผลของแผนภาพไล่สีได้
ออบเจ็กต์ชนิดนั้นอยู่ในมอดูลย่อยหนึ่งของ matplotlib ชื่อ colors
ขอเริ่มด้วยการยกตัวอย่างการใช้แล้วจึงอธิบายทีหลัง
ตัวอย่าง พิมพ์ตามนี้จะได้ผลเหมือนกับตัวอย่างที่แล้ว
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
cnorm = mpl.colors.Normalize(vmin=-3,vmax=3)
x,y = np.meshgrid(np.linspace(-10,10,101),np.linspace(-10,10,101))
z = np.sin(x)+np.sin(y)*4
z[50,50] = 30
plt.pcolor(x,y,z,cmap='rainbow',norm=cnorm)
plt.colorbar()
plt.show()
import matplotlib.pyplot as plt
import matplotlib as mpl
cnorm = mpl.colors.Normalize(vmin=-3,vmax=3)
x,y = np.meshgrid(np.linspace(-10,10,101),np.linspace(-10,10,101))
z = np.sin(x)+np.sin(y)*4
z[50,50] = 30
plt.pcolor(x,y,z,cmap='rainbow',norm=cnorm)
plt.colorbar()
plt.show()
ข้อแตกต่างจากตัวอย่างที่แล้วก็คือแทนที่จะกำหนด vmin=-3,vmax=3 ตรงฟังก์ชัน plt.pcolor โดยตรงก็ไปสร้างออบเจ็กต์ mpl.colors.Normalize ขึ้น
cnorm = mpl.colors.Normalize(vmin=-3,vmax=3)
จากนั้นจึงนำออบเจ็กต์ cnorm นี้มาใส่เป็นคีย์เวิร์ด norm ในฟังก์ชัน plt.pcolor อีกที
plt.pcolor(x,y,z,cmap='rainbow',norm=cnorm)
cnorm ที่สร้างขึ้นมานั้นที่จริงแล้วก็คือเป็นฟังก์ชันที่ทำการแปลงตัวเลขจาก -3 ถึง 3 ให้เป็น 0 ถึง 1 นั่นเอง ลองดู
for c in np.linspace(-3,3,11):
print('cnorm(%s) = %s'%(c,cnorm(c)))
print('cnorm(%s) = %s'%(c,cnorm(c)))
จะได้
cnorm(-3.0) = 0.0
cnorm(-2.4) = 0.1
cnorm(-1.8) = 0.2
cnorm(-1.2) = 0.3
cnorm(-0.6) = 0.4
cnorm(0.0) = 0.5
cnorm(0.6) = 0.6
cnorm(1.2) = 0.7
cnorm(1.8) = 0.8
cnorm(2.4) = 0.9
cnorm(3.0) = 1.0
cnorm(-2.4) = 0.1
cnorm(-1.8) = 0.2
cnorm(-1.2) = 0.3
cnorm(-0.6) = 0.4
cnorm(0.0) = 0.5
cnorm(0.6) = 0.6
cnorm(1.2) = 0.7
cnorm(1.8) = 0.8
cnorm(2.4) = 0.9
cnorm(3.0) = 1.0
ที่จริงแล้วหากแค่ต้องการปรับขอบเขตการไล่สีเฉยๆก็แค่ใส่คีย์เวิร์ด vmin และ vmax ลงใน plt.pcolor ตามเดิมก็ได้ ไม่ต่างกัน
อย่างไรก็ตามออบเจ็กต์สำหรับนอร์มาไลซ์นั้นไม่ได้มีเพียงแค่ตัวนอร์มาไลซ์รูปแบบเชิงเส้นง่ายๆอย่างที่เห็นนี้เสมอไป แต่ยังมีตัวนอร์มาไลซ์ในรูปแบบอื่นๆด้วย
ในที่นี้จะยกตัวอย่างที่น่าจะมีโอกาสได้ใช้บ่อยมาส่วนหนึ่ง
การไล่สีแบบเรขาคณิต
บางครั้งการไล่สีแบบเป็นเชิงเส้นก็อาจไม่ทำให้เราเห็นภาพอะไรบางอย่างชัดเจนมากพอ
ตัวอย่างเช่นกราฟที่ค่าสีเปลี่ยนค่าไปตามเลขยกกำลัง
x,y = np.meshgrid(np.linspace(-10,10,101),np.linspace(-10,10,101))
z = 2**x+2**y
plt.pcolor(x,y,z,cmap='rainbow')
plt.colorbar()
plt.show()
z = 2**x+2**y
plt.pcolor(x,y,z,cmap='rainbow')
plt.colorbar()
plt.show()

แบบนี้จะเห็นว่าสีมาเปลี่ยนตรงแถวขอบอย่างรวดเร็ว แต่หากปรับการไล่สีให้ไล่แบบเรขาคณิตแทนก็จะแสดงผลได้ดีขึ้น ซึ่งเราสามารถทำได้โดยการใช้ตัวนอร์มาไลซ์แบบเรขาคณิต
ลองดูตัวอย่างการใช้
x,y = np.meshgrid(np.linspace(-10,10,101),np.linspace(-10,10,101))
z = 2**x+2**y
clognorm = mpl.colors.LogNorm()
plt.pcolor(x,y,z,cmap='rainbow',norm=clognorm)
plt.colorbar()
plt.show()
z = 2**x+2**y
clognorm = mpl.colors.LogNorm()
plt.pcolor(x,y,z,cmap='rainbow',norm=clognorm)
plt.colorbar()
plt.show()

เท่านี้ก็จะเห็นว่าการไล่สีกลายเป็นแบบเรขาคณิต แถบสีทางขวาก็กลายเป็นเลขยกกำลังฐานสิบด้วย
ในที่นี้ส่วนที่เปลี่ยนแปลงไปมีแค่เราเพิ่ม mpl.colors.LogNorm() เข้ามาเป็นคีย์เวิร์ดใน plt.pcolor
mpl.colors.LogNorm นี้เป็นออบเจ็กต์นอร์มาไลซ์แบบไล่ตามยกกำลังสิบ
สามารถใส่อาร์กิวเมนต์ vmin vmax เพื่อกำหนดขอบเขตได้เช่นเดียวกับ mpl.colors.Normalize
ลองแก้ clognorm เป็น
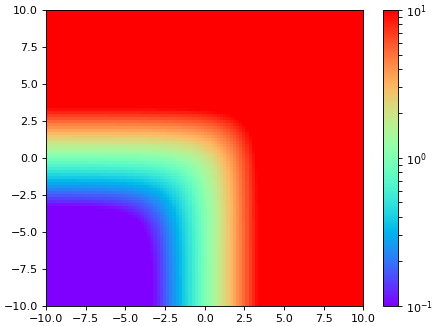
clognorm = mpl.colors.LogNorm(vmin=0.1,vmax=10)

ก็จะได้การไล่สีแค่ในช่วง 0.1 ถึง 10
ไล่สีแบบเป็นช่วงๆไม่ต่อเนื่อง
อีกรูปแบบหนึ่งที่อาจได้ใช้บ่อยก็คือการไล่สีแบบแบ่งเป็นลำดับขั้นไม่ต่อเนื่อง เป็นฟังก์ชันขั้นบันได
เราสามารถสร้างฟังก์ชันขั้นบันไดได้ด้วย mpl.colors.BoundaryNorm
ตัวอย่าง
x = np.linspace(0,2,101)
y = x**2
b = [0.,0.4,0.8,1.2,1.6,2.,2.4,2.8,3.2,3.6,4.]
cbn = mpl.colors.BoundaryNorm(b,40)
print(cbn(y))
y = x**2
b = [0.,0.4,0.8,1.2,1.6,2.,2.4,2.8,3.2,3.6,4.]
cbn = mpl.colors.BoundaryNorm(b,40)
print(cbn(y))
ผลลัพธ์
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4 4 4 4 4
4 4 4 4 4 4 4 4 8 8 8 8 8 8 8 8 8 8 13 13 13 13 13 13 13 13 13 17 17 17 17
17 17 17 21 21 21 21 21 21 21 26 26 26 26 26 26 30 30 30 30 30 30 34 34 34
34 34 39 39 39 39 39 40]
4 4 4 4 4 4 4 4 8 8 8 8 8 8 8 8 8 8 13 13 13 13 13 13 13 13 13 17 17 17 17
17 17 17 21 21 21 21 21 21 21 26 26 26 26 26 26 30 30 30 30 30 30 34 34 34
34 34 39 39 39 39 39 40]
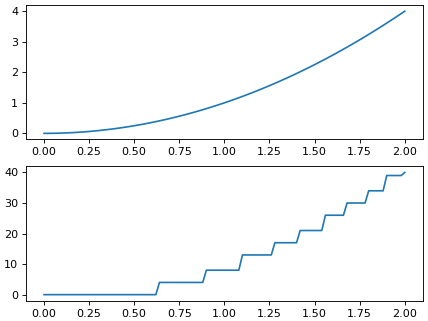
ลองเอามาวาดกราฟเทียบระหว่างฟังก์ชัน y เดิมกับ y ที่ถูกแปลงค่าเป็นขั้นบันได
plt.subplot(2,1,1)
plt.plot(x,y)
plt.subplot(2,1,2)
plt.plot(x,cbn(y))
plt.show()
plt.plot(x,y)
plt.subplot(2,1,2)
plt.plot(x,cbn(y))
plt.show()

จะเห็นว่าฟังก์ชัน y ถูกแบ่งค่าออกเป็นช่วงๆตามค่า ค่ายิ่งมากก็ย่ิงอยู่ในขั้นที่สูง
จากที่เดิมเป็นค่าที่เพิ่มขึ้นเรื่อยๆอย่างต่อเนื่อง กลายมาเป็นว่าค่าเพิ่มขึ้นเป็นขั้นๆไม่ต่อเนื่อง ถ้าหากนี่เป็นค่าที่แทนสีก็จะได้ว่าสีเห็นสีเปลี่ยนไปเป็นช่วงๆ
กลับมาดูที่เลขที่ใส่ลงในฟังก์ชัน mpl.colors.BoundaryNorm อาร์กิวเมนต์ตัวแรกคือลิสต์หรืออาเรย์ของจุดแบ่งขีดที่ต้องการ ในที่นี้แบ่งทีละ 0.4 ไปเรื่อยๆจนถึงค่าสูงสุดคือ 4 รวมแล้วแบ่งเป็น 10 ช่วง (แต่ในลิสต์ต้องมี 11 ค่า)
ส่วนอาร์กิวเมนต์ตัวหลังคือค่าตัวเลขสูงสุด ค่าเป็นจำนวนเต็มเท่านั้น ค่าผลลัพธ์ที่ได้ออกมานั้นจะไล่ตั้งแต่ 0 ไปจนถึงตัวเลขที่กำหนดนี้ ในที่นี้กำหนดเป็น 40 ดังนั้นจึงไล่ตั้งแต่ 0 ถึง 40
โดยทั่วไปเมื่อนำมาใช้จริงจะกำหนดค่าเป็น 256 เพื่อจะนำมาใช้เป็นค่าใส่ในคัลเลอร์แม็ป
ที่จริงคัลเลอร์แม็ปนั้นนอกจากจะนอร์มาไลซ์เป็น 0 ถึง 1 แล้ว หาค่าที่ใส่ลงไปเป็นจำนวนเต็มจะเป็นการไล่ตั้งแต่ 0 ถึง 255 แทน
print(plt.get_cmap('rainbow')(0)) # ได้ (0.5, 0.0, 1.0, 1.0)
print(plt.get_cmap('rainbow')(1)) # ได้ (0.49215686274509807, 0.012319659535238442, 0.99998102734872685, 1.0)
print(plt.get_cmap('rainbow')(32)) # ได้ (0.24901960784313726, 0.38410574917192586, 0.98063477046897773, 1.0)
print(plt.get_cmap('rainbow')(224)) # ได้ (1.0, 0.37270199199091436, 0.18980109344182594, 1.0)
print(plt.get_cmap('rainbow')(255)) # ได้ (1.0, 1.2246467991473532e-16, 6.123233995736766e-17, 1.0)
print(plt.get_cmap('rainbow')(256)) # ได้ (1.0, 1.2246467991473532e-16, 6.123233995736766e-17, 1.0)
print(plt.get_cmap('rainbow')(1.)) # ได้ (1.0, 1.2246467991473532e-16, 6.123233995736766e-17, 1.0)
print(plt.get_cmap('rainbow')(1)) # ได้ (0.49215686274509807, 0.012319659535238442, 0.99998102734872685, 1.0)
print(plt.get_cmap('rainbow')(32)) # ได้ (0.24901960784313726, 0.38410574917192586, 0.98063477046897773, 1.0)
print(plt.get_cmap('rainbow')(224)) # ได้ (1.0, 0.37270199199091436, 0.18980109344182594, 1.0)
print(plt.get_cmap('rainbow')(255)) # ได้ (1.0, 1.2246467991473532e-16, 6.123233995736766e-17, 1.0)
print(plt.get_cmap('rainbow')(256)) # ได้ (1.0, 1.2246467991473532e-16, 6.123233995736766e-17, 1.0)
print(plt.get_cmap('rainbow')(1.)) # ได้ (1.0, 1.2246467991473532e-16, 6.123233995736766e-17, 1.0)
จะเห็นว่า plt.get_cmap('rainbow')(1) กับ plt.get_cmap('rainbow')(1.) ได้ค่าไม่เท่ากัน แต่ plt.get_cmap('rainbow')(1.) กลับเท่ากับ plt.get_cmap('rainbow')(255) แทน เพราะการใส่ค่าเป็นเลขจำนวนจริงกับจำนวนเต็มนั้นคิดต่างกัน ต้องระวังตรงนี้ด้วย
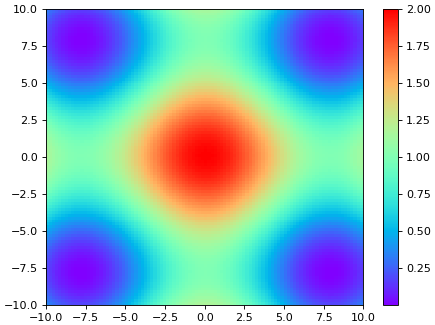
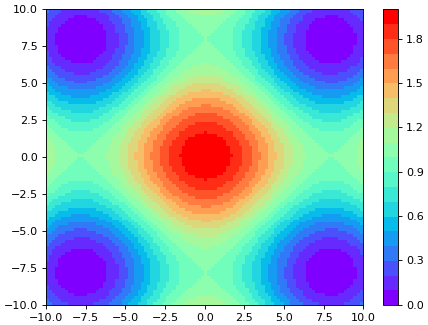
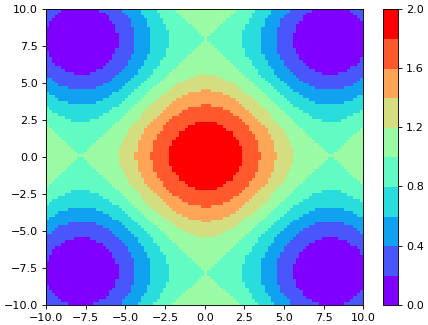
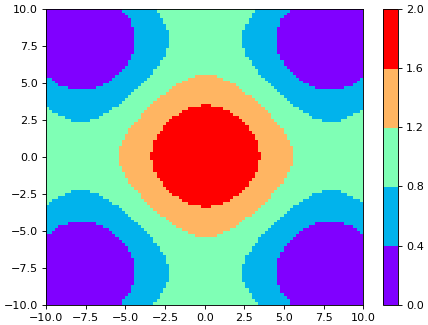
เมื่อเข้าใจแล้วคราวนี้ก็มาลองใช้ mpl.colors.BoundaryNorm กับแผนภาพไล่สีกันดูเลย ลองให้วาดภาพขึ้นมาหลายภาพ ภาพแรกเป็นการไล่สีแบบต่อเนื่อง ส่วนสามภาพที่เหลือให้วาดภาพโดยแบ่งสีเป็นขั้นๆ โดยมีจำนวนขั้นต่างออกไปเป็น 20, 10 และ 5 ตามลำดับ
x,y = np.meshgrid(np.linspace(-10,10,101),np.linspace(-10,10,101))
z = np.cos(x/5)**2+np.cos(y/5)**2
# แผนภาพไล่สีต่อเนื่อง
plt.figure()
plt.pcolor(x,y,z,cmap='rainbow')
plt.colorbar()
# แบ่งเป็น 20 ช่วง
plt.figure()
cbn = mpl.colors.BoundaryNorm(np.linspace(0,2,21),256)
plt.pcolor(x,y,z,cmap='rainbow',norm=cbn)
plt.colorbar()
# แบ่งเป็น 10 ช่วง
plt.figure()
cbn = mpl.colors.BoundaryNorm(np.linspace(0,2,11),256)
plt.pcolor(x,y,z,cmap='rainbow',norm=cbn)
plt.colorbar()
# แบ่งเป็น 5 ช่วง
plt.figure()
cbn = mpl.colors.BoundaryNorm(np.linspace(0,2,6),256)
plt.pcolor(x,y,z,cmap='rainbow',norm=cbn)
plt.colorbar()
plt.show()
z = np.cos(x/5)**2+np.cos(y/5)**2
# แผนภาพไล่สีต่อเนื่อง
plt.figure()
plt.pcolor(x,y,z,cmap='rainbow')
plt.colorbar()
# แบ่งเป็น 20 ช่วง
plt.figure()
cbn = mpl.colors.BoundaryNorm(np.linspace(0,2,21),256)
plt.pcolor(x,y,z,cmap='rainbow',norm=cbn)
plt.colorbar()
# แบ่งเป็น 10 ช่วง
plt.figure()
cbn = mpl.colors.BoundaryNorm(np.linspace(0,2,11),256)
plt.pcolor(x,y,z,cmap='rainbow',norm=cbn)
plt.colorbar()
# แบ่งเป็น 5 ช่วง
plt.figure()
cbn = mpl.colors.BoundaryNorm(np.linspace(0,2,6),256)
plt.pcolor(x,y,z,cmap='rainbow',norm=cbn)
plt.colorbar()
plt.show()




แผนภาพไล่สีที่มีการแบ่งสีเป็นขั้นๆแบบนี้เรียกว่าคอนทัวร์ (contour) บางกรณีก็ช่วยให้เห็นภาพอะไรได้ชัดขึ้นกว่าการไล่สีต่อเนื่อง
อย่างไรก็ตามที่จริงนอกจากวิธีนี้แล้ว matplotlib ก็มีฟังก์ชันสำหรับสร้างคอนทัวร์โดยเฉพาะและดีกว่า ซึ่งจะกล่าวถึงในบทที่ ๒๘ ต่อไป
นอกจากรูปแบบการนอร์มาไลซ์ที่กล่าวมาข้างต้นแล้วนั้น ความจริงแล้วเรายังสามารถสร้างรูปแบบเฉพาะขึ้นมาเองได้อีกด้วย
อ้างอิง
http://qiita.com/supersaiakujin/items/ca47200393180a693bdf
http://qiita.com/kenmatsu4/items/fe8a2f1c34c8d5676df8
http://qa.helplib.com/713168
http://blog.csdn.net/rumswell/article/details/9862089
http://matplotlib.org/users/colormapnorms.html
http://qiita.com/kenmatsu4/items/fe8a2f1c34c8d5676df8
http://qa.helplib.com/713168
http://blog.csdn.net/rumswell/article/details/9862089
http://matplotlib.org/users/colormapnorms.html