การสุ่มตัวอย่างด้วยวิธีการยอมรับและปฏิเสธ (คัดเอาหรือคัดทิ้ง) แบบอย่างง่าย
เขียนเมื่อ 2020/09/15 21:11
แก้ไขล่าสุด 2022/07/10 20:35
การสุ่มค่าตามการแจกแจงที่ต้องการไม่ใช่เรื่องง่ายอย่างที่คิด
ปรากฏการณ์และสิ่งต่างๆในโลกนี้มีการสุ่มเกิดขึ้นอยู่มากมาย การแจกแจงความน่าจะเป็นของค่าที่ได้นั้นมีอยู่หลากหลายรูปแบบซึ่งเกิดขึ้นตามธรรมชาติตามเงื่อนๆต่างๆ
แต่เมื่อเราต้องการจำลองการสุ่มโดยแจกแจงแบบต่างๆในคอมพิวเตอร์แล้ว ค่าสุ่มที่คอมพิวเตอร์สามารถสร้างจำลองขึ้นได้ง่ายที่สุดคือการแจกแจงแบบเอกรูป (uniform) คือค่าเท่ากันสม่ำเสมอในช่วงที่กำหนด ซึ่งมักมีฟังก์ชันสำหรับทำการสุ่มค่าแบบนี้ได้ง่ายๆในแต่ละภาษา เช่นไพธอนก็ random.uniform จากมอดูล random หรือ np.random.uniform จากมอดูล numpy
หรือถ้าเป็นการแจกแจงที่มีการใช้อยู่มากโดยทั่วไป ก็อาจใช้มอดูล scipy.stats (อ่านรายละเอียดได้ในบทความ การใช้ scipy.stats เพื่อทำการสุ่มด้วยการแจกแจงแบบต่างๆ)
แต่ลองคิดดูว่าหากเรามีฟังก์ชันการแจกแจงบางอย่างอยู่แล้วต้องการสุ่มให้เป็นไปตามการแจกแจงตามนั้น เราจะสร้างค่าสุ่มนั้นขึ้นได้อย่างไร?
ยกตัวอย่างเช่นต้องการสร้างค่าสุ่มโดยมีฟังก์ชันการแจกแจงเป็นแบบนี้
ถ้าลองเขียนโค้ดแล้ววาดกราฟดูค่าฟังก์ชันก็จะได้แบบนี้
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return np.where(x>=4,
np.where(x<8,(x-8)**2,0),
np.where(x>0,x**2,0)
)*3/128
x = np.linspace(0,8,201)
y = f(x)
plt.xlabel('x')
plt.ylabel(r'$\mathcal{P}(x)$')
plt.plot(x,y,'#a78629')
plt.grid(ls='--')
plt.show()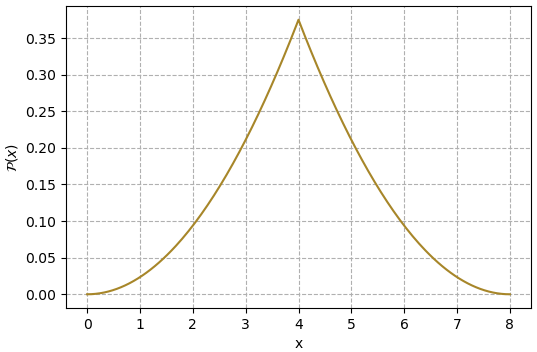
ที่จริงแล้วการแจกแจงในแบบต่างๆมีวิธีการสร้างอยู่หลากหลาย การแจกแจงแต่ละแบบก็มีอัลกอริธึมในการสร้างที่เหมาะสมที่ต่างกันออกไป
แต่โดยพื้นฐานแล้วการสุ่มแบบเอกรูปจะสร้างขึ้นได้ง่ายที่สุด ดังนั้นโดยมากแล้วการสุ่มแบบต่างๆภายในคอมพิวเตอร์มักถูกสร้างขึ้นโดยมีพื้นฐานจากการแจกแจงแบบเอกรูป แล้วค่อยแปลงเป็นแบบอื่น
ในบทความต่อจากนี้ไปตั้งใจจะอธิบายถึงวิธีการสุ่มแบบต่างๆที่สำคัญ แต่ที่ดูจะเป็นวิธีพื้นฐานที่น่าจะเข้าใจได้ง่ายที่สุดและใช้ได้ทั้่วไปที่สุดก็คือการสุ่มตัวอย่างด้วยวิธีการยอมรับและปฏิเสธ (acceptance-rejection method) ซึ่งจะอธิบายในบทความนี้
การสุ่มตัวอย่างด้วยวิธีการยอมรับและปฏิเสธ
หากให้ลองนึกวิธีดู การสุ่มตัวอย่างด้วยวิธีการยอมรับและปฏิเสธ น่าจะเป็นวิธีการสุ่มที่ง่ายที่สุดเท่าที่จะนึกออกได้ทันที
หลักการมีอยู่ง่ายๆคือทำการสุ่มแบบเอกรูปตลอดช่วงค่าที่ต้องการ แล้วก็ทำการทิ้งส่วนหนึ่งด้วยความน่าจะเป็นหนึ่ง
ยกตัวอย่างเช่นฟังก์ชันการแจกแจง f ดังที่ยกตัวอย่างมาในสมการตัวอย่างข้างบนนั้น มีขอบเขตอยู่ในช่วง 0 ถึง 8 โดยมีค่าสูงสุดอยู่ที่ 4 คือ 0.375
งั้นเราก็ทำการสุ่มค่าทั้งหมดแบบเอกรูปตลอดตั้งแต่ 0 ถึง 8 แล้วคัดทิ้งออกด้วยความน่าจะเป็นที่ต่างกันออกไป โดยในเมื่อตรงกลางค่าสูงสุดคือ 0.375 งั้นก็ให้ที่ตรงนี้มีความน่าจะเป็นในการยอมรับเอาสูงสุด คือเป็น 1 แล้วตำแหน่งที่เหลือก็ลดหลั่นลงไปตามสัดส่วน
ลองเขียนโค้ดดูได้ดังนี้
n = 50000 # จำนวนค่าที่จะสุ่ม
# สุ่มค่าในช่วง 0 ถึง 8
x = np.random.uniform(0,8,n)
# สุ่มค่าเพื่อเป็นตัวตัดสินว่าจะคัดทิ้งหรือไม่
r = np.random.uniform(0,1,n)
fx = f(x) # f(x) คำนวณค่าฟังก์ชันการแจกแจง (ซึ่งนิยามไปแล้วด้านบน ในที่นี้ขอไม่เขียนซ้ำ)
# เอาผลการสุ่มมาตัดสินว่าตัวไหนจะยอมรับหรือคัดทิ้ง
x_ao = x[r<fx/0.375]
plt.xlabel('x')
# วาดฮิสโทแกรม
plt.hist(x_ao,50,fc='#ee1368',ec='k')
plt.grid(ls='--')
plt.show()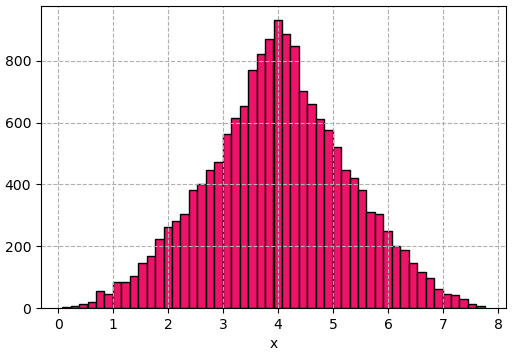
จะเห็นว่าได้การแจกแจงออกมาตามแบบที่ต้องการเลย ซึ่งถ้าเข้าใจวิธีการตามตัวอย่างนี้แล้ว ก็คงจะเอาไปประยุกต์ใช้เพื่อสร้างการแจกแจงอะไรต่างๆได้อีกมากมายตามที่ต้องการ ดูแล้วไม่ยากเลย
ปัญหาของวิธีการยอมรับและปฏิเสธ
การสุ่มตัวอย่างด้วยวิธีการยอมรับและปฏิเสธซึ่งดูเหมือนจะเข้าใจได้ง่ายๆนี้ จริงๆแล้วมีปัญหาร้ายแรงที่สุด นั่นคือเรื่องของสมรรถภาพ
นั่นเพราะเราต้องทำการสุ่มค่าขึ้นมาเป็นจำนวนมากมาย แต่กลับต้องทิ้งส่วนหนึ่งไปโดยที่ไม่ได้ใช้
เพื่อให้เห็นภาพชัน ลองเอาฟังก์ชันเดิมนี้มาทำการสุ่มแล้ววาดแสดงการแจกแจงคู่กับค่า r ที่ใช้เป็นตัวคัด
n = 1000 # จำนวนที่จะสุ่ม
x = np.random.uniform(0,8,n)
r = np.random.uniform(0,1,n) # ตัวตัดสินว่าจะคัดทิ้งหรือไม่
ao_mai = r<f(x)/0.375 # ให้ระบายสีต่างกันระหว่างค่าที่เอากับที่คัดทิ้ง
plt.xlabel('x')
plt.ylabel('r')
plt.scatter(x,r,c=ao_mai,alpha=0.6,ec='k',cmap='winter')
plt.show()
print(ao_mai.sum()) # แสดงจำนวนที่เอา ต่างกันไปแล้วแต่การสุ่มแต่ละครั้ง แต่ส่วนใหญ่ควรจะได้ 3 ร้อยกว่า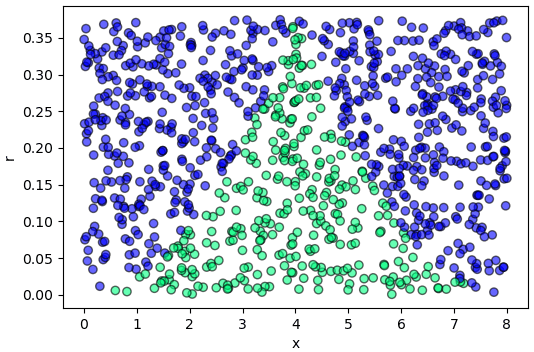
ค่า r ในที่นี้เป็นตัวคัดว่าจะเอาหรือไม่เอา โดยขึ้นกับฟังก์ชัน f เป็นตัวกำหนดว่าจะเอาในอัตราแค่ไหน ในภาพนี้สีเขียวแสดงจุดที่ถูกคัดเอา สีน้ำเงินคือที่ถูกคัดทิ้ง
จะเห็นว่าเกินกว่าครึ่ง (600 กว่า จาก 1000) ถูกคัดทิ้งไป ดังนั้นเท่ากับต้องสุ่มค่าขึ้นมาเป็นจำนวนมากเกินกว่าจำเป็นเพื่อจะเอามาทิ้ง
สำหรับในตัวอย่างนี้มีแค่หนึ่งมิติ อาจจะไม่เห็นภาพชัดมาก แต่ถ้ายิ่งมีการสุ่มหลายมิติ ก็ต้องสุ่มค่าในแต่ละมิติเป็นขอบเขตกว้างขวางเผื่อเอาไว้ อัตราการยอมรับเอาจะยิ่งน้อยลงกว่านี้ ในขณะที่ส่วนใหญ่จะถูกโยนทิ้งไปเลย ดังนั้นยิ่งถ้าค่าที่ต้องการสุ่มนั้นเป็นการแจกแจงในหลายมิติ ยิ่งไม่อาจใช้วิธีนี้ได้จริงๆง่ายๆในทางปฏิบัติ
อีกอย่างคือในตัวอย่างนี้การแจกแจงอยู่ในขอบเขตที่จำกัด (เช่น 0≤x≤8) จึงสามารถทำแบบนี้ได้ แต่ฟังก์ชันการแจกแจงทั่วไปอาจเป็นจำนวนใดๆตั้งแต่ลบอนันต์ถึงอนันต์ การใช้วิธีนี้ก็ยิ่งจะยากขึ้น
ดังนั้นโดยสรุปแล้ว วิธีการสุ่มแบบนี้อาจใช้ได้ง่ายที่สุด จึงเป็นทางเลือกที่อาจจะใช้เมื่อไม่ได้ต้องการประสิทธิภาพอะไรนัก หรือเป็นการสุ่มในมิติเดียวที่มีขอบเขตแน่นอนและอัตราการทิ้งไม่มากนัก หรือไม่ก็ไม่รู้ว่าจะใช้วิธีอื่นได้อย่างไรดี
วิธีนี้จึงควรค่าแก่การรู้ไว้เป็นพื้นฐาน เพราะใช้งานได้แน่นอน แต่ถ้ารู้ว่าการแจกแจงในแบบที่เราต้องการนั้นสามารถสร้างได้ด้วยวิธีอื่นที่มีประสิทธิภาพกว่าก็อาจควรใช้วิธีนั้นแทนมากกว่า
หากเป็นรูปแบบการแจกแจงที่ถูกใช้ทั่วไปก็จะมีอยู่ใน scipy.stats การเลือกใช้ scipy.stats จึงอาจเป็นทางเลือกที่ดีที่สุดและนิยมที่สุดเมื่อใช้ไพธอน
ซึ่งการสุ่มการแจกแจงแบบต่างๆในมอดูล scipy.stats เองก็เลือกใช้อัลกอริธึมที่เหมาะที่สุดในการสุ่มการแจกแจงแบบนั้นๆ โดยแต่ละแบบก็จะมีวิธีที่ต่างกันออกไป
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คณิตศาสตร์ >> ความน่าจะเป็น-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> การสุ่ม