pytorch เบื้องต้น บทที่ ๔: การสร้างชั้นคำนวณ
เขียนเมื่อ 2018/09/08 09:56
แก้ไขล่าสุด 2022/07/09 15:14
>> ต่อจาก บทที่ ๓
ภายในมอดูล pytorch มีมอดูลย่อยชื่อ torch.nn ซึ่งบรรจุคลาสและฟังก์ชันต่างๆสำหรับใช้ในโครงข่ายประสาทเทียม (nn ย่อมาจาก neural network นั่นเอง)
ส่วนประกอบที่สำคัญที่สุดในการประกอบโครงข่ายประสาทเทียมก็คือ ชั้นของฟังก์ชันคำนวณต่างๆ
เช่น ชั้นสำหรับคำนวณเชิงเส้น ชั้นแบบนี้เรียกว่า affine layer แต่ใน pytorch ใช้ชื่อว่า Linear (ส่วนใน keras เรียกว่า Dense)
ชั้นคำนวณพวกนี้จะมีเทนเซอร์ที่ใช้เป็นพารามิเตอร์อยู่ภายในตัว
ชั้น Linear จะมีพารามิเตอร์ค่าน้ำหนักอยู่ที่แอตทริบิวต์ .weight และค่าไบแอสที่ .bias
ค่าที่ต้องกำหนดขณะสร้างคือ (จำนวนตัวแปรขาเข้า, จำนวนตัวแปรขาออก)
น้ำหนักจะเป็นเทนเซอร์สองมิติที่มีขนาดเป็น (ขาออก, ขาเข้า) ส่วนไบแอสจะเป็นเทนเซอร์หนึ่งมิติ ขนาดเท่ากับจำนวนตัวแปรขาออก
ลองสร้างชั้นขึ้นมาแล้วดูพารามิเตอร์ภายใน
ได้
จะเห็นว่าพารามิเตอร์ก็คือเทนเซอร์ตัวนึงที่ requires_grad=True หมายความว่าเป็นเทนเซอร์ที่ขณะที่คำนวณจะมีการบันทึกค่าความชัน
นอกจากนี้หากใช้เมธอด .parameters() จะคืนพารามิเตอร์ทั้งหมดออกมาในรูปของเจเนอเรเตอร์ ถ้านำมาแปลงเป็นลิสต์ก็จะแสดงค่าทั้งหมดได้
ได้
คำสั่งนี้มีประโยชน์เวลาใช้กับออปทิไมเซอร์ ซึ่งจะกล่าวถึงในบทถัดไป
ค่าของพารามิเตอร์เหล่านี้ได้มาจากการสุ่มเอา ซึ่งโดยมาตรฐานแล้วใน pytorch จะสุ่มพารามิเตอร์ตั้งต้นให้กระจายสม่ำเสมอในขอบเขต
..(4.1)
เพียงแต่ว่าเราสามารถป้อนค่าเป็นจำนวนที่ต้องการแทนได้ทันทีถ้าต้องการ
เช่น ถ้าต้องการให้สุ่มแจกแจงแบบปกติก็ใช้ .normal_(μ,σ) ถ้าต้องการให้สุ่มแจกแจงแบบสม่ำเสมอก็ใช้ .uniform_(ต่ำสุด,สูงสุด)
ได้
สำหรับไบแอสนั้นในบางกรณีอาจไม่จำเป็นต้องใช้ จะกำหนดให้ไม่มีก็ได้ โดยกำหนด bias=0 ตอนสร้าง
เวลาที่ป้อนเทนเซอร์ผ่านชั้นนี้จะเกิดการคำนวณโดยคูณเมทริกซ์เข้ากับน้ำหนักและบวกด้วยไบแอส
..(4.2)
ตัวอย่างเช่น
..(4.3)
ได้
การถดถอยเชิงเส้น
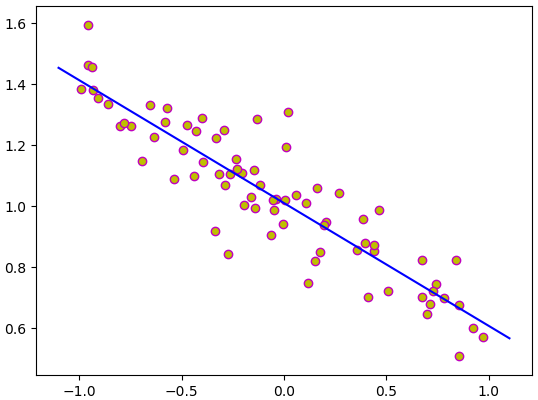
ลองทำการแก้ปัญหาการถดถอยเชิงเส้นแบบเดียวกับในบทที่แล้ว แต่คราวนี้ใช้ Linear
ต่อมาลองดูตัวอย่างกรณีตัวแปรต้นสองตัว
การใช้ชั้นคำนวณแบบนี้ทำให้การคำนวณสะดวกขึ้น แต่ก็ยังคงต้องมาคอยเขียนคำสั่งปรับพารามิเตอร์แล้วก็ล้างค่าอนุพันธ์กันเอาเองอยู่
แต่ว่า pytorch ได้เตรียมอุปกรณ์ที่สะดวกที่ทำให้ขั้นตอนตรงนี้ง่ายขึ้นไปอีก คือการใช้ออปทิไมเซอร์ ซึ่งจะพูดถึงในบทต่อไป
>> อ่านต่อ บทที่ ๕
ภายในมอดูล pytorch มีมอดูลย่อยชื่อ torch.nn ซึ่งบรรจุคลาสและฟังก์ชันต่างๆสำหรับใช้ในโครงข่ายประสาทเทียม (nn ย่อมาจาก neural network นั่นเอง)
ส่วนประกอบที่สำคัญที่สุดในการประกอบโครงข่ายประสาทเทียมก็คือ ชั้นของฟังก์ชันคำนวณต่างๆ
เช่น ชั้นสำหรับคำนวณเชิงเส้น ชั้นแบบนี้เรียกว่า affine layer แต่ใน pytorch ใช้ชื่อว่า Linear (ส่วนใน keras เรียกว่า Dense)
ชั้นคำนวณพวกนี้จะมีเทนเซอร์ที่ใช้เป็นพารามิเตอร์อยู่ภายในตัว
ชั้น Linear จะมีพารามิเตอร์ค่าน้ำหนักอยู่ที่แอตทริบิวต์ .weight และค่าไบแอสที่ .bias
ค่าที่ต้องกำหนดขณะสร้างคือ (จำนวนตัวแปรขาเข้า, จำนวนตัวแปรขาออก)
น้ำหนักจะเป็นเทนเซอร์สองมิติที่มีขนาดเป็น (ขาออก, ขาเข้า) ส่วนไบแอสจะเป็นเทนเซอร์หนึ่งมิติ ขนาดเท่ากับจำนวนตัวแปรขาออก
ลองสร้างชั้นขึ้นมาแล้วดูพารามิเตอร์ภายใน
import torch
lin = torch.nn.Linear(2,3)
print(lin)
print(lin.weight)
print(type(lin.weight))
print(lin.bias)
print(type(lin.bias))ได้
Linear(in_features=2, out_features=3, bias=True)
Parameter containing:
tensor([[-0.1785, -0.5299],
[ 0.2429, -0.5276],
[-0.5432, 0.4851]], requires_grad=True)
<class 'torch.nn.parameter.Parameter'>
Parameter containing:
tensor([-0.0320, -0.2327, 0.3440], requires_grad=True)
<class 'torch.nn.parameter.Parameter'>จะเห็นว่าพารามิเตอร์ก็คือเทนเซอร์ตัวนึงที่ requires_grad=True หมายความว่าเป็นเทนเซอร์ที่ขณะที่คำนวณจะมีการบันทึกค่าความชัน
นอกจากนี้หากใช้เมธอด .parameters() จะคืนพารามิเตอร์ทั้งหมดออกมาในรูปของเจเนอเรเตอร์ ถ้านำมาแปลงเป็นลิสต์ก็จะแสดงค่าทั้งหมดได้
lin = torch.nn.Linear(4,3)
print(lin.parameters())
print(list(lin.parameters()))ได้
[Parameter containing:
tensor([[-0.3537, -0.0335, -0.0530, 0.1352],
[-0.4223, -0.1825, 0.1712, -0.1660],
[ 0.0511, 0.1635, 0.2365, 0.0601]], requires_grad=True), Parameter containing:
tensor([-0.4955, -0.1421, -0.2290], requires_grad=True)]คำสั่งนี้มีประโยชน์เวลาใช้กับออปทิไมเซอร์ ซึ่งจะกล่าวถึงในบทถัดไป
ค่าของพารามิเตอร์เหล่านี้ได้มาจากการสุ่มเอา ซึ่งโดยมาตรฐานแล้วใน pytorch จะสุ่มพารามิเตอร์ตั้งต้นให้กระจายสม่ำเสมอในขอบเขต
..(4.1)
เพียงแต่ว่าเราสามารถป้อนค่าเป็นจำนวนที่ต้องการแทนได้ทันทีถ้าต้องการ
เช่น ถ้าต้องการให้สุ่มแจกแจงแบบปกติก็ใช้ .normal_(μ,σ) ถ้าต้องการให้สุ่มแจกแจงแบบสม่ำเสมอก็ใช้ .uniform_(ต่ำสุด,สูงสุด)
lin = torch.nn.Linear(6,2,bias=0)
lin.weight.data.normal_(0,1)
print(lin.weight)
lin.weight.data.uniform_(-1,1)
print(lin.weight)ได้
Parameter containing:
tensor([[ 0.8902, -0.9486, -0.8325, 0.1343, 0.7567, 1.6959],
[ 1.7581, 0.9200, -0.0738, -0.3420, 0.0989, -0.9752]],
requires_grad=True)
Parameter containing:
tensor([[ 0.3098, -0.3378, -0.4107, 0.2809, -0.8449, -0.0014],
[-0.8877, -0.9887, -0.3420, 0.3834, 0.0017, 0.9727]],
requires_grad=True)สำหรับไบแอสนั้นในบางกรณีอาจไม่จำเป็นต้องใช้ จะกำหนดให้ไม่มีก็ได้ โดยกำหนด bias=0 ตอนสร้าง
lin = torch.nn.Linear(3,4,bias=0)
print(lin) # ได้ Linear(in_features=3, out_features=4, bias=False)
print(lin.bias) # ได้ Noneเวลาที่ป้อนเทนเซอร์ผ่านชั้นนี้จะเกิดการคำนวณโดยคูณเมทริกซ์เข้ากับน้ำหนักและบวกด้วยไบแอส
..(4.2)
ตัวอย่างเช่น
..(4.3)
X = torch.Tensor([[3,1],[2,5],[0,2]])
lin = torch.nn.Linear(2,3)
lin.weight.data = torch.Tensor([[1,2],[3,4],[5,6]])
lin.bias.data = torch.Tensor([7,8,9])
print(lin(X))ได้
tensor([[12., 21., 30.],
[19., 34., 49.],
[11., 16., 21.]], grad_fn=<AddmmBackward0>)การถดถอยเชิงเส้น
ลองทำการแก้ปัญหาการถดถอยเชิงเส้นแบบเดียวกับในบทที่แล้ว แต่คราวนี้ใช้ Linear
import numpy as np
import matplotlib.pyplot as plt
# ข้อมูลตัวอย่าง
x = np.random.uniform(-1,1,75)
z = -x*0.4 + np.random.normal(1,0.1,75)
lin = torch.nn.Linear(1,1) # ทั้งตัวแปรต้นและตัวแปรตามต่างก็มีแค่ 1
x = torch.Tensor(x) # แปลงเป็นเทนเซอร์
X = x[:,None] # แม้จะมีตัวแปรแค่ตัวเดียวก็ต้องทำเป็นเทนเซอร์สองมิติ
z = torch.Tensor(z) # แปลงเป็นเทนเซอร์
eta = 0.5 # อัตราการเรียนรู้
ha_mse = torch.nn.MSELoss() # เตรียมฟังก์ชันหาค่าเสียหาย
n_thamsam = 50
for i in range(n_thamsam):
h = lin(X).flatten() # คำนวณเชิงเส้น
J = ha_mse(h,z) # คำนวณค่าเสียหาย
J.backward() # แพร่ย้อนกลับ
lin.weight.data -= eta*lin.weight.grad # ปรับพารามิเตอร์
lin.bias.data -= eta*lin.bias.grad
lin.weight.grad = None # ล้างค่าอนุพันธ์
lin.bias.grad = None
mx = np.linspace(-1.1,1.1,200)
mz = lin(torch.Tensor(mx)[:,None]).data.numpy().flatten()
plt.scatter(x,z,color='y',edgecolor='m')
plt.plot(mx,mz,'b')
plt.show()
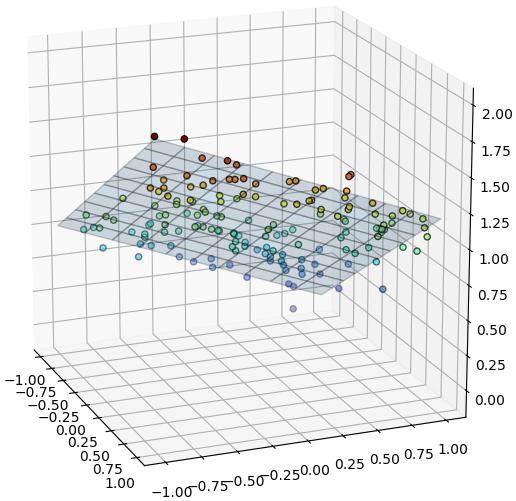
ต่อมาลองดูตัวอย่างกรณีตัวแปรต้นสองตัว
X = np.random.uniform(-1,1,[150,2])
x,y = X.T
z = x*0.6-y*0.4 + np.random.normal(1,0.1,150)
lin = torch.nn.Linear(2,1)
X = torch.Tensor(X)
z = torch.Tensor(z)
eta = 0.1
ha_mse = torch.nn.MSELoss()
n_thamsam = 200
for i in range(n_thamsam):
h = lin(X).flatten()
J = ha_mse(h,z)
J.backward()
lin.weight.data -= eta*lin.weight.grad
lin.bias.data -= eta*lin.bias.grad
lin.weight.grad = None
lin.bias.grad = None
from mpl_toolkits.mplot3d import Axes3D
mx,my = np.meshgrid(np.linspace(-1,1,11),np.linspace(-1,1,11))
mX = np.array([mx.ravel(),my.ravel()]).T
mX = torch.Tensor(mX)
mz = lin(mX).data.numpy().reshape(11,11)
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d')
ax.scatter(x,y,z,c=z,edgecolor='k',cmap='jet')
ax.plot_surface(mx,my,mz,rstride=1,cstride=1,alpha=0.2,edgecolor='k')
plt.show()
การใช้ชั้นคำนวณแบบนี้ทำให้การคำนวณสะดวกขึ้น แต่ก็ยังคงต้องมาคอยเขียนคำสั่งปรับพารามิเตอร์แล้วก็ล้างค่าอนุพันธ์กันเอาเองอยู่
แต่ว่า pytorch ได้เตรียมอุปกรณ์ที่สะดวกที่ทำให้ขั้นตอนตรงนี้ง่ายขึ้นไปอีก คือการใช้ออปทิไมเซอร์ ซึ่งจะพูดถึงในบทต่อไป
>> อ่านต่อ บทที่ ๕
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> pytorch