pytorch เบื้องต้น บทที่ ๓: อนุพันธ์ของเทนเซอร์
เขียนเมื่อ 2018/09/08 09:54
แก้ไขล่าสุด 2022/07/09 18:13
>> ต่อจาก บทที่ ๒
อนุพันธ์และการแพร่ย้อนกลับ
เทนเซอร์ของ pytorch มีคุณสมบัติในตัวที่ทำให้สามารถคำนวณค่าอนุพันธ์ได้ง่ายดาย
การจะทำให้เทนเซอร์ใช้ความสามารถเรื่องการหาอนุพันธ์ได้ก่อนอื่นต้องทำการตั้งค่าแอตทริบิวต์ .requires_grad ให้เป็น True
ถ้าหากไม่ตั้งไว้ โดยทั่วไปค่าตั้งต้นจะเป็น .requires_grad = False แบบนี้เวลาคำนวณก็จะไม่มีการเก็บค่าความชันไว้
แค่ตั้ง .requires_grad = True ไว้ เวลาใช้เทนเซอร์ตัวนั้นในการคำนวณก็จะมีการสร้างกราฟคำนวณบันทึกเส้นทางการคำนวณไว้ เชื่อมต่อกับตัวแปรที่ได้จากการคำนวณของตัวนั้น
เทนเซอร์มีเมธอด .backward() ซึ่งเมื่อพอใช้ไปแล้วจะทำการคำนวณแพร่ย้อนกลับเพื่อคำนวณอนุพันธ์ของตัวต้นทางทั้งหมด
เพียงแต่ว่าเทนเซอร์ที่คำนวณ .backward() นั้นจะต้องเป็นปริมาณเลขตัวเดียว เช่นเทนเซอร์ที่ได้จากเมธอด .sum() หรือ .mean() หรือด็อตเวกเตอร์ด้วย .matmul()
จากนั้นค่าอนุพันธ์จะถูกเก็บไว้ที่แอตทริบิวต์ .grad
ขอยกตัวอย่างง่ายๆเป็นสมการด็อตเวกเตอร์แบบนี้
..(3.1)
สร้างตัวแปรแล้วคูณกันแล้วทำการคำนวณอนุพันธ์
ในที่นี้ a เป็นตัวเริ่มต้นใช้ .backward() เองดังนั้นจะไม่มีค่า .grad
ส่วน x ไม่ได้แก้ให้ .requires_grad = True ตั้งแต่แรก จึงไม่มีค่า .grad เช่นกัน
ในขณะที่ w.grad จะได้ค่าอนุพันธ์ตามที่ควรจะเป็น คือเท่ากับ x
แต่ทีนี้ถ้าทำการคำนวณซ้ำเดิม แล้วหาอนุพันธ์อีกรอบจะพบว่าค่าที่ได้ถูกบวกเพิ่มจากค่าเดิม
ที่เป็นแบบนี้เพราะว่าค่าที่คำนวณค้างไว้จากครั้งก่อนยังอยู่ ไม่ได้ถูกเขียนทับไปแต่จะเป็นการบวกเพิ่ม
ดังนั้นก่อนการคำนวณครั้งใหม่หากไม่ต้องการให้บวกเพิ่มจะต้องทำการล้างอนุพันธ์เดิมทิ้ง โดยให้ = None
และเทนเซอร์ที่เคยใช้ .backward() ไปแล้ว ปกติถ้าทำซ้ำอีกจะ error
หากต้องการให้สามารถมีการคำนวณย้อนซ้ำได้ใหม่ต้องใส่ retain_graph=True ตอนสั่ง .backward() ครั้งแรก
ข้อควรระวัง
เรื่องหนึ่งที่ต้องระวังคือเทนเซอร์ที่ .requires_grad=True นั้นไม่สามารถแก้ค่าได้โดยตรง ถ้าจะแก้ค่าต้องพิมพ์ .data ต่อท้าย
นอกจากนี้ยังไม่สามารถแปลงเป็น numpy ได้โดยตรงด้วย ต้องพิมพ์ .data ต่อท้ายก่อนเช่นกัน
.data เป็นข้อมูลที่อยู่ภายในเทนเซอร์ ซึ่งก็เป็นเทนเซอร์เหมือนกัน แต่ว่า .requires_grad จะกลายเป็น False ดังนั้นจึงแปลงเป็นอาเรย์ของ numpy ได้ และยังสามารถแก้ค่าภายในได้
การถดถอยเชิงเส้น
ด้วยคุณสมบัติในการหาความชันได้โดยง่ายของเทนเซอร์ ทำให้นำมาใช้ในการสร้างโครงข่ายประสาทเทียมง่ายๆ
ในที่นี้จะเริ่มจากปัญหาง่ายๆอย่างการวิเคราะห์การถดถอยเชิงเส้นก่อน
ยกตัวอย่างปัญหาง่ายๆอย่างปัญหาหนึ่งมิติคือมีค่าตัวแปรต้น x และตัวแปรตาม z ซึ่งเขียนกราฟความสัมพันธ์กันดังนี้
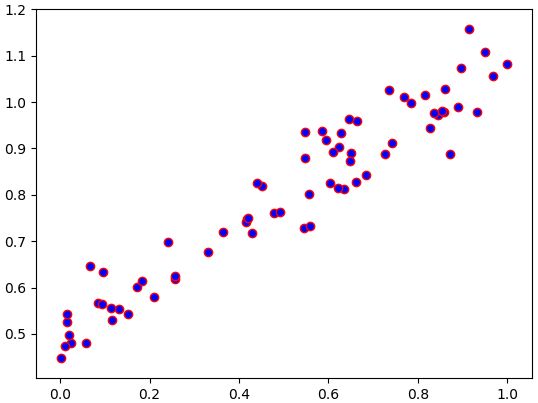
ข้อมูลและกราฟสร้างขึ้นมาจากโค้ดดังนี้
ต้องการหาฟังก์ชันของ z ในรูปของ wx+b โดยหาค่า w และ b ที่เหมาะที่สุด
เราทำได้โดยใช้วิธีการเคลื่อนลงตามความชัน คำนวณค่า h=wx+b แล้วก็เทียบกับ z แล้วหาค่าผลต่างกำลังสองเฉลี่ย
..(3.2)
จากนั้นความชันของค่าเสียหายนี้จะถูกใช้สำหรับปรับค่าพารามิเตอร์
..(3.3)
โดย η คืออัตราการเรียนรู้
ในการคำนวณค่าเสียหายผลต่างกำลังสองเฉลี่ยใน pytorch อาจใช้ torch.nn.functional.mse_loss หรือจะคำนวณโดยตรงโดยลบกันแล้วยกกำลังสองแล้วหาค่าเฉลี่ยก็ได้
นอกจากนี้อาจสร้างฟังก์ชันสำหรับหาค่าผลต่างกำลังสองเตรียมไว้จากคลาส torch.nn.MSELoss ก็ได้ ในที่นี้จะใช้วิธีนี้
เขียนโค้ดเพื่อทำการถดถอยได้ดังนี้
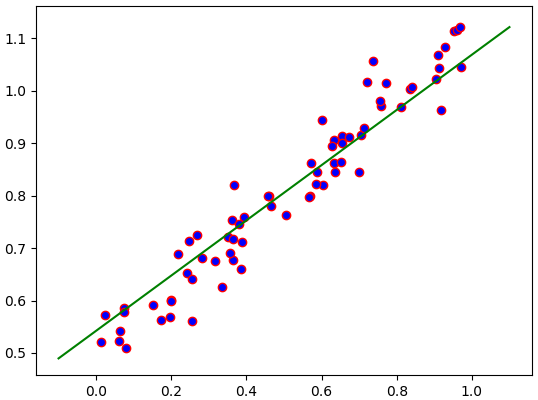
ผลออกมาได้เส้นตรงลากผ่านจุดข้อมูลอย่างเหมาะสม
วิธีการแบบนี้ดูง่ายกว่าการใช้ numpy ล้วนๆตรงที่ไม่ต้องคำนวณอนุพันธ์เอง แต่เทนเซอร์คำนวณให้อัตโนมัติด้วยเมธอด .backward()
แต่ถึงอย่างนั้นการที่ต้องคอยสร้างเทนเซอร์ของพารามิเตอร์ในชั้นคำนวณเองแบบนี้ทำให้ยังไม่สะดวกนัก จึงไม่ใช่วิธีที่ทำกันจริงๆ
วิธีที่ใช้จริงๆในการคำนวณการเคลื่อนลงตามความชันภายใน pytorch คือการใช้ชั้นคำนวณต่างๆซึ่งมีพารามิเตอร์ติดอยู่ภายใน เช่นชั้นคำนวณเชิงเส้น torch.nn.Linear ซึ่งจะกล่าวถึงบทต่อไป
>> อ่านต่อ บทที่ ๔
อนุพันธ์และการแพร่ย้อนกลับ
เทนเซอร์ของ pytorch มีคุณสมบัติในตัวที่ทำให้สามารถคำนวณค่าอนุพันธ์ได้ง่ายดาย
การจะทำให้เทนเซอร์ใช้ความสามารถเรื่องการหาอนุพันธ์ได้ก่อนอื่นต้องทำการตั้งค่าแอตทริบิวต์ .requires_grad ให้เป็น True
ถ้าหากไม่ตั้งไว้ โดยทั่วไปค่าตั้งต้นจะเป็น .requires_grad = False แบบนี้เวลาคำนวณก็จะไม่มีการเก็บค่าความชันไว้
แค่ตั้ง .requires_grad = True ไว้ เวลาใช้เทนเซอร์ตัวนั้นในการคำนวณก็จะมีการสร้างกราฟคำนวณบันทึกเส้นทางการคำนวณไว้ เชื่อมต่อกับตัวแปรที่ได้จากการคำนวณของตัวนั้น
เทนเซอร์มีเมธอด .backward() ซึ่งเมื่อพอใช้ไปแล้วจะทำการคำนวณแพร่ย้อนกลับเพื่อคำนวณอนุพันธ์ของตัวต้นทางทั้งหมด
เพียงแต่ว่าเทนเซอร์ที่คำนวณ .backward() นั้นจะต้องเป็นปริมาณเลขตัวเดียว เช่นเทนเซอร์ที่ได้จากเมธอด .sum() หรือ .mean() หรือด็อตเวกเตอร์ด้วย .matmul()
จากนั้นค่าอนุพันธ์จะถูกเก็บไว้ที่แอตทริบิวต์ .grad
ขอยกตัวอย่างง่ายๆเป็นสมการด็อตเวกเตอร์แบบนี้
..(3.1)
สร้างตัวแปรแล้วคูณกันแล้วทำการคำนวณอนุพันธ์
import torch
x = torch.Tensor([1,2,3])
w = torch.Tensor([3,4,5])
w.requires_grad = True
a = torch.matmul(w,x)
a.backward()
print(a.grad) # ได้ None
print(w.grad) # ได้ tensor([1., 2., 3.])
print(x.grad) # ได้ Noneในที่นี้ a เป็นตัวเริ่มต้นใช้ .backward() เองดังนั้นจะไม่มีค่า .grad
ส่วน x ไม่ได้แก้ให้ .requires_grad = True ตั้งแต่แรก จึงไม่มีค่า .grad เช่นกัน
ในขณะที่ w.grad จะได้ค่าอนุพันธ์ตามที่ควรจะเป็น คือเท่ากับ x
แต่ทีนี้ถ้าทำการคำนวณซ้ำเดิม แล้วหาอนุพันธ์อีกรอบจะพบว่าค่าที่ได้ถูกบวกเพิ่มจากค่าเดิม
c = torch.matmul(w,x)
c.backward()
print(w.grad) # ได้ tensor([2., 4., 6.])ที่เป็นแบบนี้เพราะว่าค่าที่คำนวณค้างไว้จากครั้งก่อนยังอยู่ ไม่ได้ถูกเขียนทับไปแต่จะเป็นการบวกเพิ่ม
ดังนั้นก่อนการคำนวณครั้งใหม่หากไม่ต้องการให้บวกเพิ่มจะต้องทำการล้างอนุพันธ์เดิมทิ้ง โดยให้ = None
w.grad = None
c = torch.matmul(w,x)
c.backward()
print(w.grad) # ได้ tensor([1., 2., 3.])และเทนเซอร์ที่เคยใช้ .backward() ไปแล้ว ปกติถ้าทำซ้ำอีกจะ error
c.backward() # RuntimeErrorหากต้องการให้สามารถมีการคำนวณย้อนซ้ำได้ใหม่ต้องใส่ retain_graph=True ตอนสั่ง .backward() ครั้งแรก
w.grad = None
a = torch.matmul(w,x)
a.backward(retain_graph=True)
a.backward()
print(w.grad) # ได้ tensor([2., 4., 6.])ข้อควรระวัง
เรื่องหนึ่งที่ต้องระวังคือเทนเซอร์ที่ .requires_grad=True นั้นไม่สามารถแก้ค่าได้โดยตรง ถ้าจะแก้ค่าต้องพิมพ์ .data ต่อท้าย
w = torch.Tensor([7,1])
w.requires_grad = True
w += 1 # RuntimeError
print(w.data) # ได้ tensor([7., 1.])
w.data += 1
print(w.data) # ได้ tensor([8., 2.])
print(w) # ได้ tensor([8., 2.], requires_grad=True)นอกจากนี้ยังไม่สามารถแปลงเป็น numpy ได้โดยตรงด้วย ต้องพิมพ์ .data ต่อท้ายก่อนเช่นกัน
w = torch.Tensor([4,6])
w.requires_grad = True
w.numpy() # RuntimeError
print(w.data.requires_grad) # ได้ False
print(w.data.numpy()) # ได้ [ 4. 6.].data เป็นข้อมูลที่อยู่ภายในเทนเซอร์ ซึ่งก็เป็นเทนเซอร์เหมือนกัน แต่ว่า .requires_grad จะกลายเป็น False ดังนั้นจึงแปลงเป็นอาเรย์ของ numpy ได้ และยังสามารถแก้ค่าภายในได้
การถดถอยเชิงเส้น
ด้วยคุณสมบัติในการหาความชันได้โดยง่ายของเทนเซอร์ ทำให้นำมาใช้ในการสร้างโครงข่ายประสาทเทียมง่ายๆ
ในที่นี้จะเริ่มจากปัญหาง่ายๆอย่างการวิเคราะห์การถดถอยเชิงเส้นก่อน
ยกตัวอย่างปัญหาง่ายๆอย่างปัญหาหนึ่งมิติคือมีค่าตัวแปรต้น x และตัวแปรตาม z ซึ่งเขียนกราฟความสัมพันธ์กันดังนี้

ข้อมูลและกราฟสร้างขึ้นมาจากโค้ดดังนี้
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(0,1,70)
z = x*0.6+np.random.normal(0.5,0.05,70)
plt.scatter(x,z,c='b',edgecolor='r')
plt.show()ต้องการหาฟังก์ชันของ z ในรูปของ wx+b โดยหาค่า w และ b ที่เหมาะที่สุด
เราทำได้โดยใช้วิธีการเคลื่อนลงตามความชัน คำนวณค่า h=wx+b แล้วก็เทียบกับ z แล้วหาค่าผลต่างกำลังสองเฉลี่ย
..(3.2)
จากนั้นความชันของค่าเสียหายนี้จะถูกใช้สำหรับปรับค่าพารามิเตอร์
..(3.3)
โดย η คืออัตราการเรียนรู้
ในการคำนวณค่าเสียหายผลต่างกำลังสองเฉลี่ยใน pytorch อาจใช้ torch.nn.functional.mse_loss หรือจะคำนวณโดยตรงโดยลบกันแล้วยกกำลังสองแล้วหาค่าเฉลี่ยก็ได้
นอกจากนี้อาจสร้างฟังก์ชันสำหรับหาค่าผลต่างกำลังสองเตรียมไว้จากคลาส torch.nn.MSELoss ก็ได้ ในที่นี้จะใช้วิธีนี้
เขียนโค้ดเพื่อทำการถดถอยได้ดังนี้
x = torch.Tensor(x) # แปลงอาเรย์เป็นเทนเซอร์เพื่อจะใช้
z = torch.Tensor(z)
w = torch.tensor(0.) # พารามิเตอร์น้ำหนัก
w.requires_grad = True
b = torch.tensor(0.) # พารามิเตอรไบแอส
b.requires_grad = True
eta = 0.1 # อัตราการเรียนรู้
ha_mse = torch.nn.MSELoss() # เตรียมฟังก์ชันหาค่าเสียหาย
n_thamsam = 100 # จำนวนรอบที่จะทำซ้ำ
for i in range(n_thamsam):
h = x*w+b # หาคำตอบจากการคำนวณ
J = ha_mse(h,z) # คำนวณค่าเสียหาย
#หรือ J = ((h-z)**2).mean()
#หรือ J = torch.nn.functional.mse_loss(h,z)
J.backward() # ทำการแพร่ย้อน
w.data -= eta*w.grad # ปรับพารามิเตอร์
b.data -= eta*b.grad
w.grad = None # ล้างค่าอนุพันธ์
b.grad = None
# แปลงค่าที่ได้ให้เป็นอาเรย์ numpy
w = w.data.numpy()
b = b.data.numpy()
# วาดกราฟแสดงผลที่ได้
mx = np.linspace(-0.1,1.1,200)
mz = mx*w+b
plt.scatter(x,z,c='b',edgecolor='r')
plt.plot(mx,mz,'g')
plt.show()
ผลออกมาได้เส้นตรงลากผ่านจุดข้อมูลอย่างเหมาะสม
วิธีการแบบนี้ดูง่ายกว่าการใช้ numpy ล้วนๆตรงที่ไม่ต้องคำนวณอนุพันธ์เอง แต่เทนเซอร์คำนวณให้อัตโนมัติด้วยเมธอด .backward()
แต่ถึงอย่างนั้นการที่ต้องคอยสร้างเทนเซอร์ของพารามิเตอร์ในชั้นคำนวณเองแบบนี้ทำให้ยังไม่สะดวกนัก จึงไม่ใช่วิธีที่ทำกันจริงๆ
วิธีที่ใช้จริงๆในการคำนวณการเคลื่อนลงตามความชันภายใน pytorch คือการใช้ชั้นคำนวณต่างๆซึ่งมีพารามิเตอร์ติดอยู่ภายใน เช่นชั้นคำนวณเชิงเส้น torch.nn.Linear ซึ่งจะกล่าวถึงบทต่อไป
>> อ่านต่อ บทที่ ๔
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> pytorch