โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๒: การเรียนรู้ของเพอร์เซปตรอน
เขียนเมื่อ 2018/08/26 23:21
แก้ไขล่าสุด 2022/07/10 21:13
>> ต่อจาก บทที่ ๑
แนวคิดในการปรับค่าพารามิเตอร์
บทที่แล้วทิ้งท้ายไว้ที่ว่าเราจะต้องเขียนโปรแกรมเพื่อให้มันทำการเรียนรู้เพื่อหาพารามิเตอร์ค่าน้ำหนักและไบแอสที่เหมาะสม
แนวคิดในการปรับพารามิเตอร์นั้นมีอยู่หลากหลาย แต่ในที่นี้จะขอเริ่มจากวิธีการที่ง่ายสุดซึ่งถูกคิดมาก่อนในช่วงยุคแรก
ในตอนแรกสุดที่เพอร์เซปตรอนถูกคิดค้นขึ้นมานั้นการปรับพารามิเตอร์ทำโดยอัลกอริธึมอย่างง่าย คือ เริ่มแรกกำหนดพารามิเตอร์ตั้งต้นขึ้นมา อาจใช้การสุ่มหรือกำหนดเอาตามความเหมาะสม จากนั้นลองคำนวณคำตอบจากเพอร์เซปตรอนขณะนั้น แล้วเทียบว่าตรงหรือเปล่า ถ้าไม่ตรงก็ทำการปรับค่า
ภาพอธิบายหลักการคร่าวๆ เราคำนวณหาคำตอบ (h) แล้วเอามาเทียบกับคำตอบจริง (z) แล้วผลที่ได้เป็นตัวกำหนดว่าจะปรับพารามิเตอร์ (w1,w2,...,wn,b) ยังไง
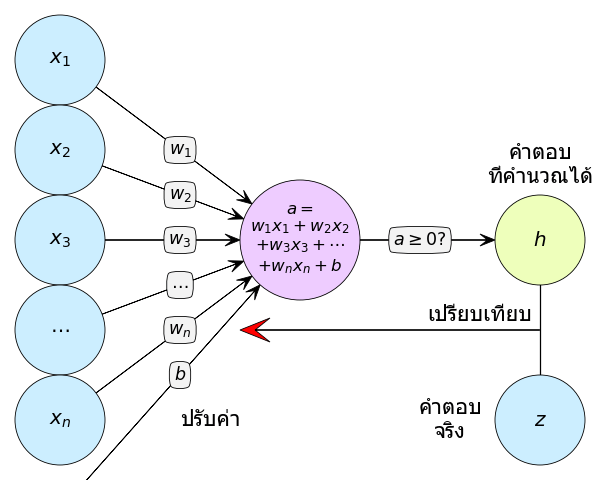
ส่วนการจะพิจารณาว่าควรปรับค่าไปยังไงนั้นจะพิจารณาง่ายๆแบบนี้ คือ
- ถ้าคำตอบจริงเป็น 1 แต่คำตอบที่คำนวณได้เป็น 0 แสดงว่าค่าที่คำนวณได้ต่ำไป ดังนั้นต้องปรับไปในทางที่ทำให้ค่าสูงขึ้น นั่นคือถ้าค่าตัวแปรไหนเป็นบวก น้ำหนักที่คูณตัวนั้นจะต้องเพิ่มค่า แต่ถ้าตัวแปรเป็นลบ น้ำหนักจะต้องลดค่า นอกจากนี้ไบแอสก็ควรต้องปรับค่าเพิ่มด้วย
- ถ้าคำตอบจริงเป็น 0 แต่คำตอบที่คำนวณได้เป็น 1 แสดงว่าค่าที่คำนวณได้สูงไป ต้องปรับให้ได้ค่าต่ำลงนั่นคือถ้าค่าตัวแปรไหนเป็นบวกก็ต้องลดค่าน้ำหนักตัวนั้น ตัวแปรไหนเป็นลบต้องเพิ่มค่าน้ำหนัก ส่วนไบแอสก็ต้องลดค่าด้วย
สรุปก็คือ พิจารณาว่าค่าไหนปรับแล้วจะทำให้การเปลี่ยนแปลงเป็นไปในทิศทางไหน ก็ปรับไปในทางที่จะทำให้คำตอบเข้าใกล้ที่ควรจะเป็นมากขึ้น
เมื่อเขียนสรุปเป็นสมการแล้วก็จะได้แบบนี้
..(2.1)
..(2.2)
โดย h(xi) คือคำตอบที่คำนวณได้จากตัวแปรต้น x ตัวที่ i ส่วน zi คือตำตอบจริงตัวที่ i ที่ใส่ดัชนี i ไปเพราะใช้ข้อมูลหลายตัวในการเรียนรู้
โดยค่า η ในที่นี้เรียกว่าอัตราการเรียนรู้ (学习率, learning rate) เป็นค่าที่กำหนดว่าในแต่ละครั้งควรจะมีการปรับค่าพารามิเตอร์ไปมากน้อยแค่ไหน
w ใน (2.1) นี้อยู่ในรูปของอาเรย์ของค่าน้ำหนักของตัวแปรต่างๆหลายตัว ถ้าแยกให้เข้าใจง่าย แต่ละตัวจะมีการปรับค่าดังนี้
..(2.3)
กรณี zi เป็น 1 แต่ h(xi) เป็น 0 จะได้ zi-h(xi)=1 แบบนั้น b จะถูกปรับเพิ่ม ส่วน wj คือค่าน้ำหนักของตัวแปรตัวที่ j จะถูกปรับโดยขึ้นกับว่าค่า xi,j เป็นเท่าไหร่ ถ้าเป็นบวก wj ก็ถูกปรับเพิ่ม ถ้าเป็นลบก็ลด
ส่วนถ้า zi เป็น 0 แต่ h(xi) เป็น 1 ก็จะได้ zi-h(xi)=-1 แล้วการเปลี่ยนแปลงก็เป็นไปในทางตรงกันข้าม
แต่ถ้าทั้ง zi และ h(xi) เป็น 0 หรือ 1 ทั่งคู่ zi-h(xi)=0 ก็จะไม่เกิดการเปลี่ยนแปลงใดๆ
สมการที่ดูเรียบง่ายนี้สามารถใช้ปรับพารามิเตอร์ให้เป็นไปอย่างที่ต้องการได้ดีในระดับนึง แม้ว่าจะยังไม่ดีพอ (เหตุผลไว้จะกล่าวตอนหลัง)
สรุปขั้นตอน
1. ทำการกำหนดค่าพารามิเตอร์ตั้งต้นขึ้นมา
2. หยิบข้อมูลขึ้นมาตัวนึง คำนวณผลลัพธ์ของเพอร์เซปตรอนด้วยพารามิเตอร์ขณะนั้น แล้วดูว่าได้ค่าต่างจากคำตอบจริงเท่าไหร่ แล้วปรับค่า
3. ทำเหมือนเดิมกับตัวต่อไป
4. พอใช้ข้อมูลครบหมดทุกตัวก็เริ่มทำซ้ำรอบใหม่อีกรอบ พารามิเตอร์ก็จะเปลี่ยนไปเรื่อยๆ ทำไปจนกว่าจะครบจำนวนครั้งสูงสุดที่ต้องการ หรือสามารถทายถูกทั้งหมด
เขียนโปรแกรม
คราวนี้จะเขียนฟังก์ชันเพอร์เซปตรอนเหมือนคราวที่แล้ว แต่ครั้งนี้เราจะกำหนด w และ b ที่นอกฟังก์ชันเพื่อให้สามารถปรับค่าไปเรื่อยๆได้
ค่าตั้งต้นจะกำหนดเป็นอะไรก็ได้ บางทีอาจเริ่มที่ 0 ทั้งหมด หรือเอาค่าที่คาดเดาล่วงหน้า ในที่นี้ขอกำหนดเป็นเท่านี้
จากนั้นขอยกตัวอย่างเป็นเกต AND ซึ่งเป็นเกตที่จะให้ค่าเป็น 1 เมื่อค่าป้อนเข้าทั้งหมดเป็น 1 เท่านั้น ที่เหลือเป็น 0
นั่นคือ
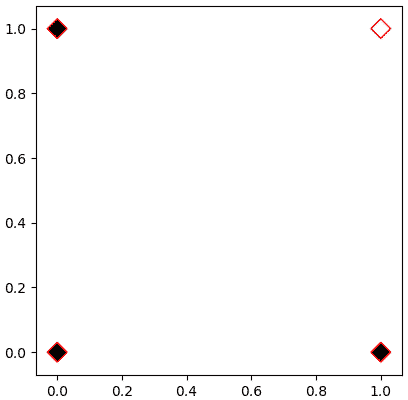
เป้าหมายของเราคือหาค่า w และ b ที่จะทำให้ h(X)==z ทุกตัว
ลองให้โปรแกรมวนซ้ำโดยทำการคำนวณตามสมการ (2.1) แล้วปรับค่าพารามิเตอร์ไปเรื่อยๆ พร้อมกันนั้นก็ให้แสดงผลค่าที่ได้ในแต่ละรอบออกมาด้วย
ผลลัพธ์จะได้
ในที่นี้การเรียนรู้ทำเสร็จสิ้นสมบูรณ์ในการวนซ้ำรอบที่ 5
จะเห็นได้ว่าค่าที่ได้จากเพอร์เซปตรอนเปลี่ยนแปลงไปเรื่อยๆจนในที่สุดก็จะกลายเป็น [0 0 0 1] ซึ่งตรงกับค่า z ที่ต้องการ
ลองวาดภาพแสดงการแบ่งตามพารามิเตอร์สุดท้ายที่ได้
ก็จะได้แบบนี้
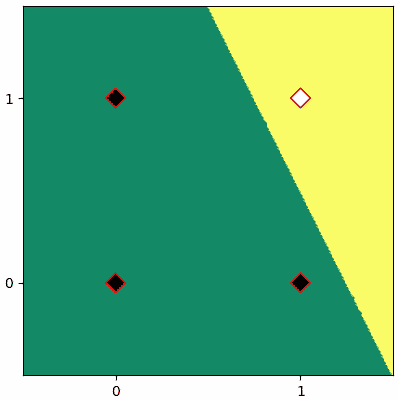
ทีนี้ถ้าวาดออกมาเป็นภาพเคลื่อนไหวแสดงความเปลี่ยนแปลงของเส้นแบ่งแล้วก็จะได้แบบนี้
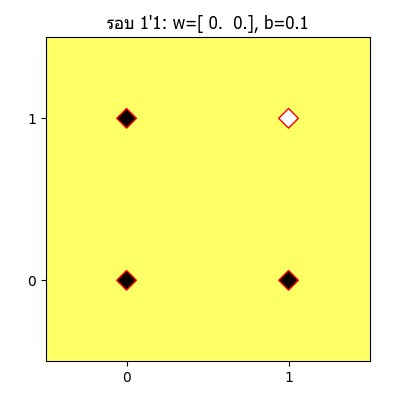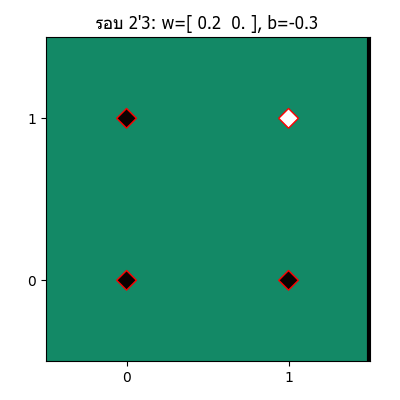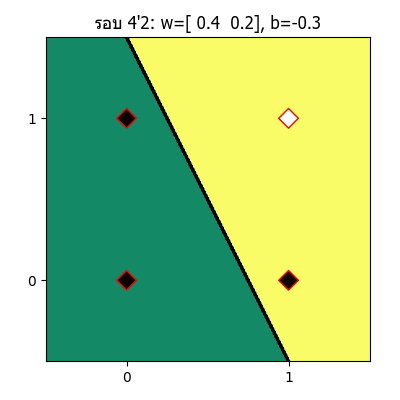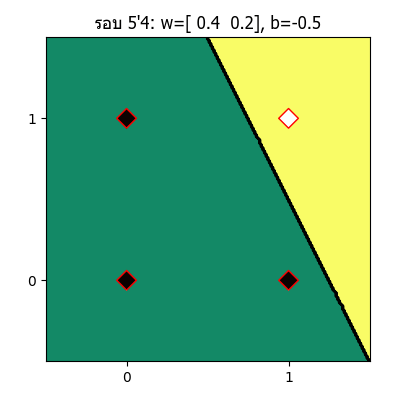
จะเห็นว่าเส้นแบ่งจะเปลี่ยนแปลงไปเรื่อยๆ จนในที่สุดเส้นสามารถแบ่งแยกระหว่างส่วนที่ควรเป็น 1 และ 0 ออกจากกันได้อย่างถูกต้อง
ปัญหาของวิธีนี้
นี่เป็นอัลกอริธึมอย่างง่ายๆในการหาค่าน้ำหนักและไบแอสที่เหมาะสม อย่างไรก็ตาม วิธีการนี้มีปัญหาอยู่มาก
อย่างแรกคือ เพอร์เซปตรอนไม่สามารถใช้ในกรณีของปัญหาที่ไม่สามารถแบ่งเชิงเส้นได้โดยสมบูรณ์ เช่น
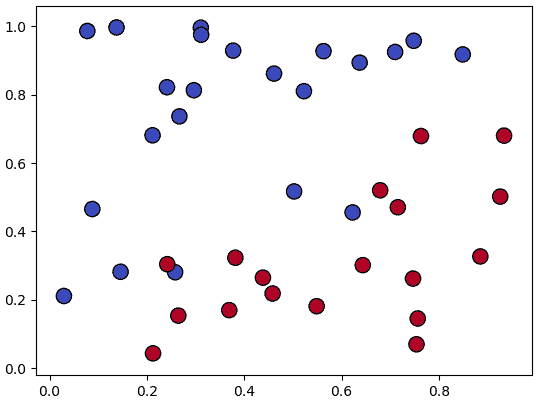
แบบนี้ไม่ว่าจะปรับค่าน้ำหนักและไบแอสไปสักกี่ครั้งก็ไม่มีทางแบ่งได้สมบูรณ์ และเพอร์เซปตรอนจะทำการปรับค่าไปเรื่อยๆไม่มีที่สิ้นสุด
อีกปัญหาคือ ต่อให้แบ่งได้ก็ตาม แต่เส้นที่สามารถแบ่งได้นั้นก็ไม่ได้มีอยู่แบบเดียว จะรู้ได้อย่างไรว่าคำตอบที่ได้มานั้นดีที่สุดแล้ว
เช่นดูอย่างภาพนี้
จะเห็นว่าเส้นสีเขียวดูจะแบ่งได้ดีที่สุดแต่เส้นอื่นก็แบ่งได้เช่นกัน
แต่หากใช้วิธีการแบบที่กล่าวมานี้ในการแบ่งละก็ผลที่ได้อาจไม่ได้คำตอบที่ดีที่สุด ขอแค่ระหว่างเรียนรู้ไปมานั้นได้เส้นแบ่งแบบไหนที่สามารถแยกข้อมูลได้สมบูรณ์ก่อน การเรียนรู้ก็จะหยุดที่ตรงนั้นทันทีเลย
ด้วยปัญหานี้ทำให้อัลกอริธึมอย่างง่ายของเพอร์เซปตรอนแบบนี้ไม่เหมาะที่จะนำมาใช้งานจริง
ในบทต่อไปจะแนะนำวิธีการที่ถูกนำมาใช้งานจริง นั่นคือ การเคลื่อนลงตามความชัน (梯度下降法, gradient descent) กับฟังก์ชันกระตุ้น (激活函数, activation function)
กล่าวโดยสรุปแล้ว วิธีการปรับพารามิเตอร์ของเพอร์เซปตรอนดังที่อธิบายในบทนี้อาจไม่ใช่วิธีที่ดีพอที่จะนำมาใช้งานจริง แต่ถึงอย่างนั้นก็ให้แนวคิดเบื้องต้นกับเราได้ จึงมีค่าที่จะเรียนรู้ถึงมันสักเล็กน้อย
ที่จริงยังมีรายละเอียดอื่นๆอีก แต่ไม่จำเป็นต้องพูดถึงมากแล้วเพราะเป้าหมายคือแค่แนะนำให้รู้จักหลักการคร่าวๆ ที่จะต้องไปเน้นจริงๆคือวิธีการในบทต่อไป
>> อ่านต่อ บทที่ ๓
แนวคิดในการปรับค่าพารามิเตอร์
บทที่แล้วทิ้งท้ายไว้ที่ว่าเราจะต้องเขียนโปรแกรมเพื่อให้มันทำการเรียนรู้เพื่อหาพารามิเตอร์ค่าน้ำหนักและไบแอสที่เหมาะสม
แนวคิดในการปรับพารามิเตอร์นั้นมีอยู่หลากหลาย แต่ในที่นี้จะขอเริ่มจากวิธีการที่ง่ายสุดซึ่งถูกคิดมาก่อนในช่วงยุคแรก
ในตอนแรกสุดที่เพอร์เซปตรอนถูกคิดค้นขึ้นมานั้นการปรับพารามิเตอร์ทำโดยอัลกอริธึมอย่างง่าย คือ เริ่มแรกกำหนดพารามิเตอร์ตั้งต้นขึ้นมา อาจใช้การสุ่มหรือกำหนดเอาตามความเหมาะสม จากนั้นลองคำนวณคำตอบจากเพอร์เซปตรอนขณะนั้น แล้วเทียบว่าตรงหรือเปล่า ถ้าไม่ตรงก็ทำการปรับค่า
ภาพอธิบายหลักการคร่าวๆ เราคำนวณหาคำตอบ (h) แล้วเอามาเทียบกับคำตอบจริง (z) แล้วผลที่ได้เป็นตัวกำหนดว่าจะปรับพารามิเตอร์ (w1,w2,...,wn,b) ยังไง

ส่วนการจะพิจารณาว่าควรปรับค่าไปยังไงนั้นจะพิจารณาง่ายๆแบบนี้ คือ
- ถ้าคำตอบจริงเป็น 1 แต่คำตอบที่คำนวณได้เป็น 0 แสดงว่าค่าที่คำนวณได้ต่ำไป ดังนั้นต้องปรับไปในทางที่ทำให้ค่าสูงขึ้น นั่นคือถ้าค่าตัวแปรไหนเป็นบวก น้ำหนักที่คูณตัวนั้นจะต้องเพิ่มค่า แต่ถ้าตัวแปรเป็นลบ น้ำหนักจะต้องลดค่า นอกจากนี้ไบแอสก็ควรต้องปรับค่าเพิ่มด้วย
- ถ้าคำตอบจริงเป็น 0 แต่คำตอบที่คำนวณได้เป็น 1 แสดงว่าค่าที่คำนวณได้สูงไป ต้องปรับให้ได้ค่าต่ำลงนั่นคือถ้าค่าตัวแปรไหนเป็นบวกก็ต้องลดค่าน้ำหนักตัวนั้น ตัวแปรไหนเป็นลบต้องเพิ่มค่าน้ำหนัก ส่วนไบแอสก็ต้องลดค่าด้วย
สรุปก็คือ พิจารณาว่าค่าไหนปรับแล้วจะทำให้การเปลี่ยนแปลงเป็นไปในทิศทางไหน ก็ปรับไปในทางที่จะทำให้คำตอบเข้าใกล้ที่ควรจะเป็นมากขึ้น
เมื่อเขียนสรุปเป็นสมการแล้วก็จะได้แบบนี้
..(2.1)
..(2.2)
โดย h(xi) คือคำตอบที่คำนวณได้จากตัวแปรต้น x ตัวที่ i ส่วน zi คือตำตอบจริงตัวที่ i ที่ใส่ดัชนี i ไปเพราะใช้ข้อมูลหลายตัวในการเรียนรู้
โดยค่า η ในที่นี้เรียกว่าอัตราการเรียนรู้ (学习率, learning rate) เป็นค่าที่กำหนดว่าในแต่ละครั้งควรจะมีการปรับค่าพารามิเตอร์ไปมากน้อยแค่ไหน
w ใน (2.1) นี้อยู่ในรูปของอาเรย์ของค่าน้ำหนักของตัวแปรต่างๆหลายตัว ถ้าแยกให้เข้าใจง่าย แต่ละตัวจะมีการปรับค่าดังนี้
..(2.3)
กรณี zi เป็น 1 แต่ h(xi) เป็น 0 จะได้ zi-h(xi)=1 แบบนั้น b จะถูกปรับเพิ่ม ส่วน wj คือค่าน้ำหนักของตัวแปรตัวที่ j จะถูกปรับโดยขึ้นกับว่าค่า xi,j เป็นเท่าไหร่ ถ้าเป็นบวก wj ก็ถูกปรับเพิ่ม ถ้าเป็นลบก็ลด
ส่วนถ้า zi เป็น 0 แต่ h(xi) เป็น 1 ก็จะได้ zi-h(xi)=-1 แล้วการเปลี่ยนแปลงก็เป็นไปในทางตรงกันข้าม
แต่ถ้าทั้ง zi และ h(xi) เป็น 0 หรือ 1 ทั่งคู่ zi-h(xi)=0 ก็จะไม่เกิดการเปลี่ยนแปลงใดๆ
สมการที่ดูเรียบง่ายนี้สามารถใช้ปรับพารามิเตอร์ให้เป็นไปอย่างที่ต้องการได้ดีในระดับนึง แม้ว่าจะยังไม่ดีพอ (เหตุผลไว้จะกล่าวตอนหลัง)
สรุปขั้นตอน
1. ทำการกำหนดค่าพารามิเตอร์ตั้งต้นขึ้นมา
2. หยิบข้อมูลขึ้นมาตัวนึง คำนวณผลลัพธ์ของเพอร์เซปตรอนด้วยพารามิเตอร์ขณะนั้น แล้วดูว่าได้ค่าต่างจากคำตอบจริงเท่าไหร่ แล้วปรับค่า
3. ทำเหมือนเดิมกับตัวต่อไป
4. พอใช้ข้อมูลครบหมดทุกตัวก็เริ่มทำซ้ำรอบใหม่อีกรอบ พารามิเตอร์ก็จะเปลี่ยนไปเรื่อยๆ ทำไปจนกว่าจะครบจำนวนครั้งสูงสุดที่ต้องการ หรือสามารถทายถูกทั้งหมด
เขียนโปรแกรม
คราวนี้จะเขียนฟังก์ชันเพอร์เซปตรอนเหมือนคราวที่แล้ว แต่ครั้งนี้เราจะกำหนด w และ b ที่นอกฟังก์ชันเพื่อให้สามารถปรับค่าไปเรื่อยๆได้
import numpy as np
def h(X):
a = np.dot(X,w) + b
return (a>=0).astype(int)
w = np.array([0,0.])
b = 0.1ค่าตั้งต้นจะกำหนดเป็นอะไรก็ได้ บางทีอาจเริ่มที่ 0 ทั้งหมด หรือเอาค่าที่คาดเดาล่วงหน้า ในที่นี้ขอกำหนดเป็นเท่านี้
จากนั้นขอยกตัวอย่างเป็นเกต AND ซึ่งเป็นเกตที่จะให้ค่าเป็น 1 เมื่อค่าป้อนเข้าทั้งหมดเป็น 1 เท่านั้น ที่เหลือเป็น 0
นั่นคือ
X = np.array([
[0,0],
[0,1],
[1,0],
[1,1]
])
z = np.array([0,0,0,1])
# วาดภาพแสดง
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='r',marker='D',cmap='hot')
plt.show()
เป้าหมายของเราคือหาค่า w และ b ที่จะทำให้ h(X)==z ทุกตัว
ลองให้โปรแกรมวนซ้ำโดยทำการคำนวณตามสมการ (2.1) แล้วปรับค่าพารามิเตอร์ไปเรื่อยๆ พร้อมกันนั้นก็ให้แสดงผลค่าที่ได้ในแต่ละรอบออกมาด้วย
eta = 0.2 # อัตราการเรียนรู้
print('เริ่มต้น: h(x)=%s, w=%s, b=%s'%(h(X),w,b))
for j in range(100): # ให้ทำซ้ำสูงสุด 100 ครั้ง
for i in range(4):
z_h = z[i] - h(X[i])
dw = eta*z_h*X[i]
db = eta*z_h
w += dw
b += db
print('รอบ %d.%d: h(x)=%s, w=%s, b=%s, Δw=%s, Δb=%s'%(j+1,i+1,h(X),w,b,dw,db))
if(np.all(h(X)==z)): # ถ้าผลลัพธ์ถูกต้องทั้งหมดก็ให้เสร็จสิ้นการเรียนรู้
breakผลลัพธ์จะได้
เริ่มต้น: h(x)=[1 1 1 1], w=[ 0. 0.], b=0.1
รอบ 1.1: h(x)=[0 0 0 0], w=[ 0. 0.], b=-0.1, Δw=[-0. -0.], Δb=-0.2
รอบ 1.2: h(x)=[0 0 0 0], w=[ 0. 0.], b=-0.1, Δw=[ 0. 0.], Δb=0.0
รอบ 1.3: h(x)=[0 0 0 0], w=[ 0. 0.], b=-0.1, Δw=[ 0. 0.], Δb=0.0
รอบ 1.4: h(x)=[1 1 1 1], w=[ 0.2 0.2], b=0.1, Δw=[ 0.2 0.2], Δb=0.2
รอบ 2.1: h(x)=[0 1 1 1], w=[ 0.2 0.2], b=-0.1, Δw=[-0. -0.], Δb=-0.2
รอบ 2.2: h(x)=[0 0 0 0], w=[ 0.2 0. ], b=-0.3, Δw=[-0. -0.2], Δb=-0.2
รอบ 2.3: h(x)=[0 0 0 0], w=[ 0.2 0. ], b=-0.3, Δw=[ 0. 0.], Δb=0.0
รอบ 2.4: h(x)=[0 1 1 1], w=[ 0.4 0.2], b=-0.1, Δw=[ 0.2 0.2], Δb=0.2
รอบ 3.1: h(x)=[0 1 1 1], w=[ 0.4 0.2], b=-0.1, Δw=[ 0. 0.], Δb=0.0
รอบ 3.2: h(x)=[0 0 1 1], w=[ 0.4 0. ], b=-0.3, Δw=[-0. -0.2], Δb=-0.2
รอบ 3.3: h(x)=[0 0 0 0], w=[ 0.2 0. ], b=-0.5, Δw=[-0.2 -0. ], Δb=-0.2
รอบ 3.4: h(x)=[0 0 1 1], w=[ 0.4 0.2], b=-0.3, Δw=[ 0.2 0.2], Δb=0.2
รอบ 4.1: h(x)=[0 0 1 1], w=[ 0.4 0.2], b=-0.3, Δw=[ 0. 0.], Δb=0.0
รอบ 4.2: h(x)=[0 0 1 1], w=[ 0.4 0.2], b=-0.3, Δw=[ 0. 0.], Δb=0.0
รอบ 4.3: h(x)=[0 0 0 0], w=[ 0.2 0.2], b=-0.5, Δw=[-0.2 -0. ], Δb=-0.2
รอบ 4.4: h(x)=[0 1 1 1], w=[ 0.4 0.4], b=-0.3, Δw=[ 0.2 0.2], Δb=0.2
รอบ 5.1: h(x)=[0 1 1 1], w=[ 0.4 0.4], b=-0.3, Δw=[ 0. 0.], Δb=0.0
รอบ 5.2: h(x)=[0 0 0 1], w=[ 0.4 0.2], b=-0.5, Δw=[-0. -0.2], Δb=-0.2
รอบ 5.3: h(x)=[0 0 0 1], w=[ 0.4 0.2], b=-0.5, Δw=[ 0. 0.], Δb=0.0
รอบ 5.4: h(x)=[0 0 0 1], w=[ 0.4 0.2], b=-0.5, Δw=[ 0. 0.], Δb=0.0ในที่นี้การเรียนรู้ทำเสร็จสิ้นสมบูรณ์ในการวนซ้ำรอบที่ 5
จะเห็นได้ว่าค่าที่ได้จากเพอร์เซปตรอนเปลี่ยนแปลงไปเรื่อยๆจนในที่สุดก็จะกลายเป็น [0 0 0 1] ซึ่งตรงกับค่า z ที่ต้องการ
ลองวาดภาพแสดงการแบ่งตามพารามิเตอร์สุดท้ายที่ได้
mx,my = np.meshgrid(np.linspace(-0.5,1.5,200),np.linspace(-0.5,1.5,200))
mX = np.array([mx.ravel(),my.ravel()]).T
mz = h(mX).reshape(200,-1)
plt.axes(aspect=1,xticks=[0,1],yticks=[0,1])
plt.contourf(mx,my,mz,cmap='summer',vmin=0,vmax=1)
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='r',marker='D',cmap='hot')
plt.show()ก็จะได้แบบนี้

ทีนี้ถ้าวาดออกมาเป็นภาพเคลื่อนไหวแสดงความเปลี่ยนแปลงของเส้นแบ่งแล้วก็จะได้แบบนี้

จะเห็นว่าเส้นแบ่งจะเปลี่ยนแปลงไปเรื่อยๆ จนในที่สุดเส้นสามารถแบ่งแยกระหว่างส่วนที่ควรเป็น 1 และ 0 ออกจากกันได้อย่างถูกต้อง
ปัญหาของวิธีนี้
นี่เป็นอัลกอริธึมอย่างง่ายๆในการหาค่าน้ำหนักและไบแอสที่เหมาะสม อย่างไรก็ตาม วิธีการนี้มีปัญหาอยู่มาก
อย่างแรกคือ เพอร์เซปตรอนไม่สามารถใช้ในกรณีของปัญหาที่ไม่สามารถแบ่งเชิงเส้นได้โดยสมบูรณ์ เช่น

แบบนี้ไม่ว่าจะปรับค่าน้ำหนักและไบแอสไปสักกี่ครั้งก็ไม่มีทางแบ่งได้สมบูรณ์ และเพอร์เซปตรอนจะทำการปรับค่าไปเรื่อยๆไม่มีที่สิ้นสุด
อีกปัญหาคือ ต่อให้แบ่งได้ก็ตาม แต่เส้นที่สามารถแบ่งได้นั้นก็ไม่ได้มีอยู่แบบเดียว จะรู้ได้อย่างไรว่าคำตอบที่ได้มานั้นดีที่สุดแล้ว
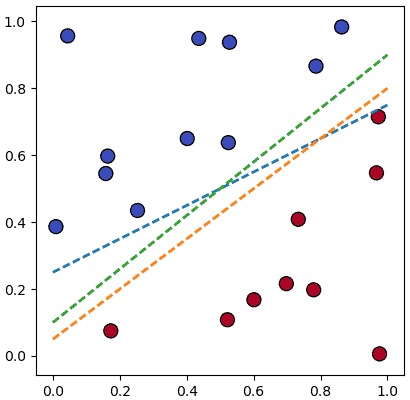
เช่นดูอย่างภาพนี้

จะเห็นว่าเส้นสีเขียวดูจะแบ่งได้ดีที่สุดแต่เส้นอื่นก็แบ่งได้เช่นกัน
แต่หากใช้วิธีการแบบที่กล่าวมานี้ในการแบ่งละก็ผลที่ได้อาจไม่ได้คำตอบที่ดีที่สุด ขอแค่ระหว่างเรียนรู้ไปมานั้นได้เส้นแบ่งแบบไหนที่สามารถแยกข้อมูลได้สมบูรณ์ก่อน การเรียนรู้ก็จะหยุดที่ตรงนั้นทันทีเลย
ด้วยปัญหานี้ทำให้อัลกอริธึมอย่างง่ายของเพอร์เซปตรอนแบบนี้ไม่เหมาะที่จะนำมาใช้งานจริง
ในบทต่อไปจะแนะนำวิธีการที่ถูกนำมาใช้งานจริง นั่นคือ การเคลื่อนลงตามความชัน (梯度下降法, gradient descent) กับฟังก์ชันกระตุ้น (激活函数, activation function)
กล่าวโดยสรุปแล้ว วิธีการปรับพารามิเตอร์ของเพอร์เซปตรอนดังที่อธิบายในบทนี้อาจไม่ใช่วิธีที่ดีพอที่จะนำมาใช้งานจริง แต่ถึงอย่างนั้นก็ให้แนวคิดเบื้องต้นกับเราได้ จึงมีค่าที่จะเรียนรู้ถึงมันสักเล็กน้อย
ที่จริงยังมีรายละเอียดอื่นๆอีก แต่ไม่จำเป็นต้องพูดถึงมากแล้วเพราะเป้าหมายคือแค่แนะนำให้รู้จักหลักการคร่าวๆ ที่จะต้องไปเน้นจริงๆคือวิธีการในบทต่อไป
>> อ่านต่อ บทที่ ๓
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy