โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๑: การสร้างโครงข่ายโดยการนิยามขณะวิ่ง
เขียนเมื่อ 2018/08/26 23:30
แก้ไขล่าสุด 2022/07/10 21:09
>> ต่อจาก บทที่ ๑๐
ในบทที่แล้วแสดงการนำชั้นมาประกอบกันเพื่อสร้างโครงข่ายประสาทเทียม
จะเห็นว่าหลังจากที่ทำการคำนวณไปข้างหน้าเสร็จก็ต้องมาเขียนขั้นตอนในการแพร่ย้อนกลับอีก
แต่ว่าจริงๆแล้วปกติเคลื่อนไปข้างหน้ายังไงก็ควรจะแพร่ย้อนกลับอย่างนั้น ตายตัวอยู่แล้ว ดังนั้นควรจะสามารถทำให้ในขณะที่ทำการคำนวณไปข้างหน้านั้นเส้นทางคำนวณการจะถูกบันทึกไปด้วย แล้วพอคำนวณไปถึงสุดท้ายก็แค่ออกคำสั่งแพร่ย้อนกลับ ก็จะเกิดการแพร่ย้อนกลับตามเส้นทางที่เดินมาจนถึงตรงนั้น
วิธีการแบบนี้เรียกว่า การนิยามขณะวิ่ง (define by run) คือเส้นทางการคำนวณได้ถูกนิยามขึ้นทันทีในขณะวิ่งคำนวณไปข้างหน้านั้นเอง
หลักการนี้ถูกนำมาใช้จริงในเฟรมเวิร์กโครงข่ายประสาทเทียมที่ได้รับความนิยมอย่าง pytorch และ chainer เราสามารถเรียนรู้จากตรงนั้นได้
เพียงแต่ว่าของจริงที่ใช้ในนั้นจะซับซ้อนกว่าที่แนะนำในนี้มาก ในที่นี้เป็นแค่การนำแนวคิดพื้นฐานมาใช้ แต่ตัดส่วนที่ซับซ้อนออกไป
หลักการคือ สร้างคลาสของตัวแปร (Tuaprae) และคลาสของชั้น (Chan) ขึ้นมาดังนี้
ส่วนคลาสของชั้นฟังก์ชันกระตุ้นและฟังก์ชันค่าเสียหายที่เคยแนะนำในบทที่แล้วก็นิยามแบบเดิมแต่ตั้งให้เป็นคลาสย่อยของคลาส Chan เพื่อให้มีเมธอด __call__ ติดมาด้วย
ออบเจ็กต์ของคลาส Chan เวลาถูกเรียกใช้จะคำนวณไปข้างหน้าตามที่นิยามในเมธอด .pai() ในคลาสย่อย จากนั้นก็สร้างออบเจ็กต์ของคลาส Tuaprae ขึ้นมา ซึ่งจะบรรจุค่า (.kha) ที่ได้ และบันทึกไว้ด้วยว่าที่มา (.thima) ของมันมาจากชั้นไหน
ค่าตัวแปรต้นที่ป้อนให้ตอนเรียกใช้ชั้นจะเป็นค่าตัวเลขธรรมดาหรือออบเจ็กต์ของคลาส Tuaprae ก็ได้ กรณีที่ค่าที่รับมาเป็น Tuaprae จะถูกบันทึกไว้ใน .tuapraeton
แบบนี้เมื่อทำการคำนวณไปข้างหน้าเรื่อยๆตัวแปรตามที่ได้ก็จะบันทึกออบเจ็กต์ชั้นที่สร้างมันมา แล้วตัวออบเจ็กต์ชันเองก็บันทึกออบเจ็กต์ตัวแปรต้นไว้ แบบนี้ต่อไปเป็นทอดๆ
Tuaprae มีเมธอด .phraeyon() สำหรับทำการเริ่มแพร่ย้อนเมื่อคำนวณจนถึงสุดแล้ว เมื่อเริ่มเมธอดนี้จะเกิดการแพร่ย้อนแล้วคำนวณอนุพันธ์ในทุกตัวแปรและชั้นที่เป็นทางผ่านไปเรื่อยๆจนถึงต้นทาง
นอกจากนี้สำหรับชั้นที่มีพารามิเตอร์อย่าง Affin ก็ปรับให้ง่ายต่อการใช้งานขึ้น โดยสร้างคลาสใหม่ชื่อ Param สำหรับเป็นพารามิเตอร์ แล้วให้เก็บทั้งค่าตัวพารามิเตอร์และอนุพันธ์ของมันไปด้วย นอกจากนี้ก็รวมพารามิเตอร์ทั้งหมดไว้เป็นลิสต์ เก็บไว้ที่ .param
ส่วนค่าไบแอส (พารามิเตอร์ตัวหลัง) ในที่นี้ให้เป็น 0 โดยมีขนาดเท่ากับค่าขาออก m1
รายละเอียดเกี่ยวกับเรื่องการกำหนดค่าพารามิเตอร์ตั้งต้นจะพูดถึงอีกทีในบทที่ ๑๓
ต่อมาลองดูตัวอย่างการนำมาใช้เพื่อสร้างคลาสของโครงข่ายประสาทเทียม
ในที่นี้ได้ลองสร้างในแบบที่แบ่งการคำนวณแต่ละส่วนแยกใส่เป็นเมธอดเพื่อให้เข้าใจง่าย
ภายในขั้นตอนวนซ้ำจะเริ่มจาก .ha_entropy() คือคำนวณไปข้างหน้าจนถึงหาเอนโทรปีออกมาเสร็จ
จากนั้นได้ค่า entropy ซึ่งเป็นออบเจ็กต์ของคลาส Tuaprae แล้วก็ใช้เมธอด .praeyon() เพื่อเริ่มการแพร่ย้อนกลับ แล้วก็จะได้ค่าอนุพันธ์ชันของพารามิเตอร์แต่ละตัวเก็บไว้
สุดท้ายก็ใช้เมธอด .prap_para() ทำการค้นว่าชั้นไหนมีพารามิเตอร์แล้วทำการปรับ แล้วพอปรับเสร็จก็ล้างค่าอนุพันธ์ให้เป็น 0 ไปด้วย
ส่วนจำนวนชั้น และจำนวนเซลล์ในแต่ละชั้นก็กำหนดโดยค่า m ตอนเริ่มสร้าง
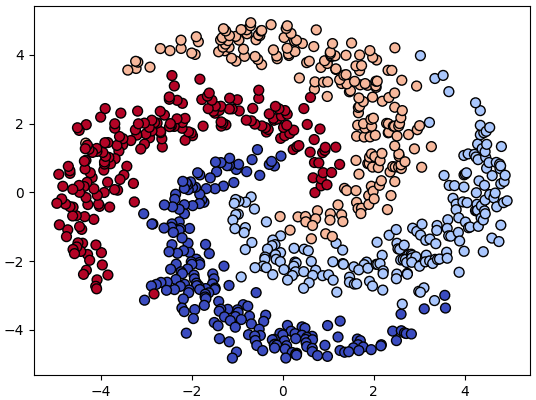
ลองพิจารณาจำแนกกลุ่มข้อมูลชุดนี้
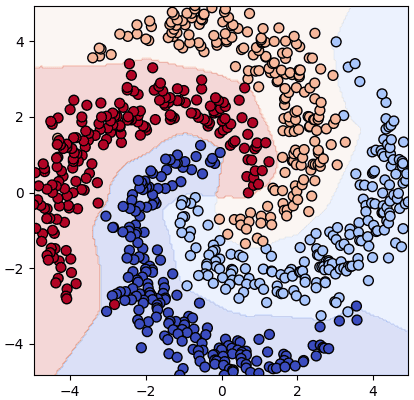
เริ่มจากลองใช้โครงข่าย ๒ ชั้น
หากต้องการเปลี่ยนโครงสร้างก็แค่แก้ตรงบรรทัดที่สร้างออบเจ็กต์ ส่วนที่เหลือเหมือนเดิม เช่นต้องการลอง ๔ ชั้นก็แก้เป็นแบบนี้
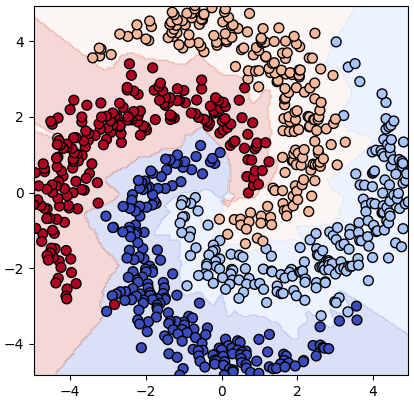
เทียบกันแล้วอาจเห็นได้ว่าแบบ ๔ ชั้นดูมีแนวโน้มที่จะแบ่งพื้นที่ออกมาซับซ้อนกว่า แต่แบบนี้ทำให้มีโอกาสเกิดการเรียนรู้เกินได้ง่าย จึงไม่ใช่ว่าชั้นเยอะแล้วจะดีเสมอไป
อาจลองปรับเปลี่ยนชั้นและจำนวนเซลล์ในแต่ละชั้น รวมถึงฟังก์ชันกระตุ้นและอัตราการเรียนรู้แล้วเทียบผลดูได้
สำหรับนิยามคลาสต่างๆที่ถูกสร้างในบทนี้จะถูกนำไปใช้ในบทต่อๆไปด้วย ไม่มีการเปลี่ยนแปลงแล้ว เพื่อให้หยิบมาใช้ได้สะดวกจึงได้รวบรวมคลาสต่างๆเอาไว้ในไฟล์ >> unagi.py
ในนี้รวมถึงสิ่งที่จะกล่าวถึงในบทถัดๆไปด้วย
>> อ่านต่อ บทที่ ๑๒
ในบทที่แล้วแสดงการนำชั้นมาประกอบกันเพื่อสร้างโครงข่ายประสาทเทียม
จะเห็นว่าหลังจากที่ทำการคำนวณไปข้างหน้าเสร็จก็ต้องมาเขียนขั้นตอนในการแพร่ย้อนกลับอีก
แต่ว่าจริงๆแล้วปกติเคลื่อนไปข้างหน้ายังไงก็ควรจะแพร่ย้อนกลับอย่างนั้น ตายตัวอยู่แล้ว ดังนั้นควรจะสามารถทำให้ในขณะที่ทำการคำนวณไปข้างหน้านั้นเส้นทางคำนวณการจะถูกบันทึกไปด้วย แล้วพอคำนวณไปถึงสุดท้ายก็แค่ออกคำสั่งแพร่ย้อนกลับ ก็จะเกิดการแพร่ย้อนกลับตามเส้นทางที่เดินมาจนถึงตรงนั้น
วิธีการแบบนี้เรียกว่า การนิยามขณะวิ่ง (define by run) คือเส้นทางการคำนวณได้ถูกนิยามขึ้นทันทีในขณะวิ่งคำนวณไปข้างหน้านั้นเอง
หลักการนี้ถูกนำมาใช้จริงในเฟรมเวิร์กโครงข่ายประสาทเทียมที่ได้รับความนิยมอย่าง pytorch และ chainer เราสามารถเรียนรู้จากตรงนั้นได้
เพียงแต่ว่าของจริงที่ใช้ในนั้นจะซับซ้อนกว่าที่แนะนำในนี้มาก ในที่นี้เป็นแค่การนำแนวคิดพื้นฐานมาใช้ แต่ตัดส่วนที่ซับซ้อนออกไป
หลักการคือ สร้างคลาสของตัวแปร (Tuaprae) และคลาสของชั้น (Chan) ขึ้นมาดังนี้
class Tuaprae(object):
def __init__(self,kha,thima=None):
self.kha = kha # ค่า
self.thima = thima # ออบเจ็กต์ Chan ที่สร้างตัวแปรนี้ขึ้นมา
def phraeyon(self,g=1):
if(self.thima is None):
return
g = self.thima.yon(g)
for tpt in self.thima.tuapraeton:
tpt.phraeyon(g)
class Chan:
def __init__(self):
'รอนิยามในคลาสย่อย'
def __call__(self,*tuaprae):
self.tuapraeton = [] # เก็บออบเจ็กต์ Tuaprae ที่ป้อนเข้ามา
kha_tuapraeton = []
for tp in tuaprae:
if(type(tp)==Tuaprae):
self.tuapraeton.append(tp)
kha_tuapraeton.append(tp.kha)
else:
kha_tuapraeton.append(tp)
kha_tuapraetam = self.pai(*kha_tuapraeton) # คำนวนไปข้างหน้า
tuapraetam = Tuaprae(kha_tuapraetam,thima=self) # สร้างออบเจ็กต์ของตัวแปรตามที่คำนวณได้
return tuapraetam
def pai(self):
'รอนิยามในคลาสย่อย'
def yon(self):
'รอนิยามในคลาสย่อย'ส่วนคลาสของชั้นฟังก์ชันกระตุ้นและฟังก์ชันค่าเสียหายที่เคยแนะนำในบทที่แล้วก็นิยามแบบเดิมแต่ตั้งให้เป็นคลาสย่อยของคลาส Chan เพื่อให้มีเมธอด __call__ ติดมาด้วย
import numpy as np
class Sigmoid(Chan):
def pai(self,a):
self.h = 1/(1+np.exp(-a))
return self.h
def yon(self,g):
return g*(1.-self.h)*self.h
class Relu(Chan):
def pai(self,x):
self.krong = (x>0)
return np.where(self.krong,x,0)
def yon(self,g):
return np.where(self.krong,g,0)
class Softmax_entropy(Chan):
def pai(self,a,Z):
self.Z = Z
exp_a = np.exp(a.T-a.max(1))
self.h = (exp_a/exp_a.sum(0)).T
return -(np.log(self.h[Z]+1e-10)).mean()
def yon(self,g):
return g*(self.h-self.Z)/len(self.h)ออบเจ็กต์ของคลาส Chan เวลาถูกเรียกใช้จะคำนวณไปข้างหน้าตามที่นิยามในเมธอด .pai() ในคลาสย่อย จากนั้นก็สร้างออบเจ็กต์ของคลาส Tuaprae ขึ้นมา ซึ่งจะบรรจุค่า (.kha) ที่ได้ และบันทึกไว้ด้วยว่าที่มา (.thima) ของมันมาจากชั้นไหน
ค่าตัวแปรต้นที่ป้อนให้ตอนเรียกใช้ชั้นจะเป็นค่าตัวเลขธรรมดาหรือออบเจ็กต์ของคลาส Tuaprae ก็ได้ กรณีที่ค่าที่รับมาเป็น Tuaprae จะถูกบันทึกไว้ใน .tuapraeton
แบบนี้เมื่อทำการคำนวณไปข้างหน้าเรื่อยๆตัวแปรตามที่ได้ก็จะบันทึกออบเจ็กต์ชั้นที่สร้างมันมา แล้วตัวออบเจ็กต์ชันเองก็บันทึกออบเจ็กต์ตัวแปรต้นไว้ แบบนี้ต่อไปเป็นทอดๆ
Tuaprae มีเมธอด .phraeyon() สำหรับทำการเริ่มแพร่ย้อนเมื่อคำนวณจนถึงสุดแล้ว เมื่อเริ่มเมธอดนี้จะเกิดการแพร่ย้อนแล้วคำนวณอนุพันธ์ในทุกตัวแปรและชั้นที่เป็นทางผ่านไปเรื่อยๆจนถึงต้นทาง
นอกจากนี้สำหรับชั้นที่มีพารามิเตอร์อย่าง Affin ก็ปรับให้ง่ายต่อการใช้งานขึ้น โดยสร้างคลาสใหม่ชื่อ Param สำหรับเป็นพารามิเตอร์ แล้วให้เก็บทั้งค่าตัวพารามิเตอร์และอนุพันธ์ของมันไปด้วย นอกจากนี้ก็รวมพารามิเตอร์ทั้งหมดไว้เป็นลิสต์ เก็บไว้ที่ .param
class Param:
def __init__(self,kha):
self.kha = kha # ค่า
self.g = 0 # อนุพันธ์
class Affin(Chan):
def __init__(self,m0,m1,sigma=0.1):
self.m = m0,m1
self.param = [Param(np.random.normal(0,sigma,self.m)),
Param(np.zeros(m1))]
def pai(self,X):
self.X = X
return np.dot(X,self.param[0].kha) + self.param[1].kha
def yon(self,g):
self.param[0].g += np.dot(self.X.T,g)
self.param[1].g += g.sum(0)
return np.dot(g,self.param[0].kha.T)ส่วนค่าไบแอส (พารามิเตอร์ตัวหลัง) ในที่นี้ให้เป็น 0 โดยมีขนาดเท่ากับค่าขาออก m1
รายละเอียดเกี่ยวกับเรื่องการกำหนดค่าพารามิเตอร์ตั้งต้นจะพูดถึงอีกทีในบทที่ ๑๓
ต่อมาลองดูตัวอย่างการนำมาใช้เพื่อสร้างคลาสของโครงข่ายประสาทเทียม
class PrasatMLP:
def __init__(self,m,s=1,eta=0.1,kratun='relu'):
self.m = m
self.eta = eta
self.chan = []
for i in range(len(m)-1):
self.chan.append(Affin(m[i],m[i+1],s))
if(i<len(m)-2):
if(kratun=='relu'):
self.chan.append(Relu())
else:
self.chan.append(Sigmoid())
self.chan.append(Softmax_entropy())
def rianru(self,X,z,n_thamsam):
Z = ha_1h(z,self.m[-1])
self.entropy = []
for i in range(n_thamsam):
entropy = self.ha_entropy(X,Z)
entropy.phraeyon()
self.prap_para()
self.entropy.append(entropy.kha)
def ha_entropy(self,X,Z):
for c in self.chan[:-1]:
X = c(X)
return self.chan[-1](X,Z)
def prap_para(self):
for c in self.chan:
if(not hasattr(c,'param')):
continue
for p in c.param:
p.kha -= self.eta*p.g
p.g = 0
def thamnai(self,X):
for c in self.chan[:-1]:
X = c(X)
return X.kha.argmax(1)ในที่นี้ได้ลองสร้างในแบบที่แบ่งการคำนวณแต่ละส่วนแยกใส่เป็นเมธอดเพื่อให้เข้าใจง่าย
ภายในขั้นตอนวนซ้ำจะเริ่มจาก .ha_entropy() คือคำนวณไปข้างหน้าจนถึงหาเอนโทรปีออกมาเสร็จ
จากนั้นได้ค่า entropy ซึ่งเป็นออบเจ็กต์ของคลาส Tuaprae แล้วก็ใช้เมธอด .praeyon() เพื่อเริ่มการแพร่ย้อนกลับ แล้วก็จะได้ค่าอนุพันธ์ชันของพารามิเตอร์แต่ละตัวเก็บไว้
สุดท้ายก็ใช้เมธอด .prap_para() ทำการค้นว่าชั้นไหนมีพารามิเตอร์แล้วทำการปรับ แล้วพอปรับเสร็จก็ล้างค่าอนุพันธ์ให้เป็น 0 ไปด้วย
ส่วนจำนวนชั้น และจำนวนเซลล์ในแต่ละชั้นก็กำหนดโดยค่า m ตอนเริ่มสร้าง
ลองพิจารณาจำแนกกลุ่มข้อมูลชุดนี้
np.random.seed(1)
r = np.tile(np.sqrt(np.linspace(0.5,25,200)),4)
t = np.random.normal(np.sqrt(r*5),0.3)
z = np.arange(4).repeat(200)
t += z*np.pi/2
X = np.array([r*np.cos(t),r*np.sin(t)]).T
plt.scatter(X[:,0],X[:,1],50,c=z,edgecolor='k',cmap='coolwarm')
plt.show()
เริ่มจากลองใช้โครงข่าย ๒ ชั้น
prasat = PrasatMLP(m=[2,50,4],eta=0.1,kratun='relu')
prasat.rianru(X,z,n_thamsam=5000)
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),200),np.linspace(X[:,1].min(),X[:,1].max(),200))
mX = np.array([mx.ravel(),my.ravel()]).T
mz = prasat.thamnai(mX).reshape(200,-1)
plt.axes(aspect=1,xlim=(X[:,0].min(),X[:,0].max()),ylim=(X[:,1].min(),X[:,1].max()))
plt.contourf(mx,my,mz,cmap='coolwarm',alpha=0.2)
plt.scatter(X[:,0],X[:,1],50,c=z,edgecolor='k',cmap='coolwarm')
plt.show()
หากต้องการเปลี่ยนโครงสร้างก็แค่แก้ตรงบรรทัดที่สร้างออบเจ็กต์ ส่วนที่เหลือเหมือนเดิม เช่นต้องการลอง ๔ ชั้นก็แก้เป็นแบบนี้
prasat = PrasatMLP(m=[2,50,50,50,4],eta=0.01,kratun='relu')
เทียบกันแล้วอาจเห็นได้ว่าแบบ ๔ ชั้นดูมีแนวโน้มที่จะแบ่งพื้นที่ออกมาซับซ้อนกว่า แต่แบบนี้ทำให้มีโอกาสเกิดการเรียนรู้เกินได้ง่าย จึงไม่ใช่ว่าชั้นเยอะแล้วจะดีเสมอไป
อาจลองปรับเปลี่ยนชั้นและจำนวนเซลล์ในแต่ละชั้น รวมถึงฟังก์ชันกระตุ้นและอัตราการเรียนรู้แล้วเทียบผลดูได้
สำหรับนิยามคลาสต่างๆที่ถูกสร้างในบทนี้จะถูกนำไปใช้ในบทต่อๆไปด้วย ไม่มีการเปลี่ยนแปลงแล้ว เพื่อให้หยิบมาใช้ได้สะดวกจึงได้รวบรวมคลาสต่างๆเอาไว้ในไฟล์ >> unagi.py
ในนี้รวมถึงสิ่งที่จะกล่าวถึงในบทถัดๆไปด้วย
>> อ่านต่อ บทที่ ๑๒
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy