โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๕: มินิแบตช์
เขียนเมื่อ 2018/08/26 23:34
แก้ไขล่าสุด 2022/07/10 21:08
>> ต่อจาก บทที่ ๑๔
ในบทที่ผ่านๆมาเราใช้ข้อมูลที่มีในการฝึกโครงข่ายประสาทเทียมทีเดียวพร้อมกันทั้งหมด
แต่ในทางปฏิบัติแล้วเรานิยมแบ่งข้อมูลเป็นกลุ่มเล็กๆแล้วคำนวณทีละกลุ่ม วิธีการนี้เรียกว่ามินิแบตช์ (minibatch)
การใช้มินิแบตช์ในการเคลื่อนลงตามความชันก็ถือว่าเป็นการเคลื่อนลงตามความชันแบบสุ่ม (随机梯度下降法, stochastic gradient descent) เช่นเดียวกับการใช้ข้อมูลแค่ทีละตัว
การใช้ข้อมูลเป็นกลุ่มแบบนี้มีความแน่นอนมากกว่าใช้ข้อมูลทีละตัว เพราะทำให้ไม่ไวต่อข้อมูลตัวใดตัวหนึ่งมากไป
และจะดีกว่าการใช้ข้อมูลทั้งหมดทีเดียวในเรื่องของความเร็วด้วย ดังนั้นจึงสามารถทั้งรักษาความแน่นอนและเวลาในการคำนวณด้วย
นอกจากนี้ยังมีข้อดีอีกอย่าง นั่นคือลดโอกาสที่จะได้คำตอบที่เป็นแค่ค่าต่ำสุดสัมพัทธ์
ค่าต่ำสุดสัมพัทธ์คือค่าที่ดูแล้วต่ำที่สุดเมื่อเทียบกับบริเวณรอบๆ แต่จริงๆแล้วอาจยังมีจุดที่ต่ำกว่านั้นอยู่ไกลออกไป
ถ้าเราใช้ข้อมูลทั้งหมดทีเดียวค่าเสียหายก็จะมีอยู่ค่าเดียว ทิศทางของการปรับค่าก็จะค่อนข้างแน่นอน แบบนั้นถ้าเจอจุดต่ำสุดสัมพัทธ์ก่อนก็จะมุ่งไปทางนั้นและได้ตรงนั้นเป็นคำตอบ
แต่ถ้าเราเปลี่ยนกลุ่มข้อมูลที่พิจารณาไปเรื่อยๆค่าเสียหายที่คำนวณได้ก็จะเปลี่ยนไปในแต่ละครั้ง โอกาสที่จะเปลี่ยนทิศทางออกจากจุดสัมพัทธ์ตรงนั้นไปเจอจุดต่ำสุดอื่นก็จะมีมากขึ้น ดังนั้นจึงกลายเป็นว่าความไม่แน่นอนที่เกิดขึ้นนี้กลับเป็นผลดีมากกว่า
ด้วยเหตุนี้ทำให้ในทางปฏิบัติแล้วมินิแบตช์เป็นที่นิยมกว่า
ลองสร้างคลาสของโครงข่ายประสาทเทียมที่คล้ายกับที่ทำไปในบทที่ ๑๒ แต่เพิ่มการใช้มินิแบตช์ลงไป จะกลายเป็นแบบนี้ (อย่าลืมโหลดคลาสของชั้นต่างๆก่อนจาก >> unagi.py)
โดยรวมแล้วดูซับซ้อนขึ้นมา เพราะต้องเพิ่มวังวน for ด้านในมาเพื่อวนทำซ้ำเพื่อหยิบข้อมูลเป็นกลุ่มๆในแต่ละรอบ
ทุกรอบจะมีจำนวนข้อมูลเท่ากันหมดยกเว้นรอบสุดท้ายจะเป็นการเก็บเศษที่เหลืออยู่ ซึ่งอาจไม่ครบตามจำนวน
ในแต่ละรอบจะเปลี่ยนกลุ่ม เปลี่ยนลำดับการสุ่มทั้งหมด
นอกจากนี้เวลาคำนวณคะแนนจะไม่คำนวณในแต่ละรอบย่อย แต่จะรอให้ใช้ข้อมูลทั้งหมดครบแล้วคำนวณทั้งหมดพร้อมกันใหม่ทีเดียว จึงได้มีการปรับปรุงเมธอด .ha_entropy() ให้สามารถเลือกที่จะคำนวณค่าคะแนนไปด้วย ทั้งคะแนนและเอนโทรปีเป็นผลจากการคำนวณไปข้างหน้าเหมือนกัน แต่ต่างตรงขั้นตอนสุดท้าย ดังนั้นถ้าต้องการทั้งสองอย่างจึงควรคำนวณพร้อมกัน
สำหรับจำนวนต่อรอบนั้นโดยทั่วไปที่คนนิยมใช้กันมากคือเลขยกกำลังของสอง เช่น 64, 128, 256 สาเหตุไม่ใช่เพราะจะทำให้ผลลัพธ์ดีกว่า แต่เป็นเหตุผลในแง่ของความเร็ว เพราะคอมพิวเตอร์เก็บข้อมูลในรูปแบบของเลขฐานสองเป็นหลัก
ยังไงจำนวนต่อรอบต่างกันเล็กน้อยก็ไม่ได้มีผลกระทบต่อผลลัพธ์ ดังนั้นการเลือกค่าที่ทำให้คำนวณได้เร็วจึงกลายเป็นปัจจัยที่ถูกพิจารณาไป
ลองนำมาใช้จำแนกข้อมูลหน้าตาซับซ้อนแบบนี้
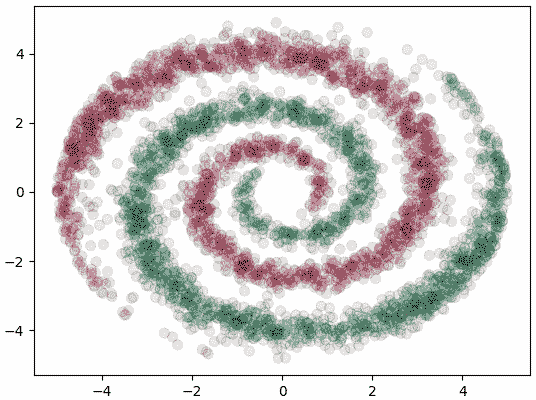
ให้ทำการแบ่งเขตพร้อมทั้งแสดงค่าเอนโทรปีและคะแนนการทำนายด้วย
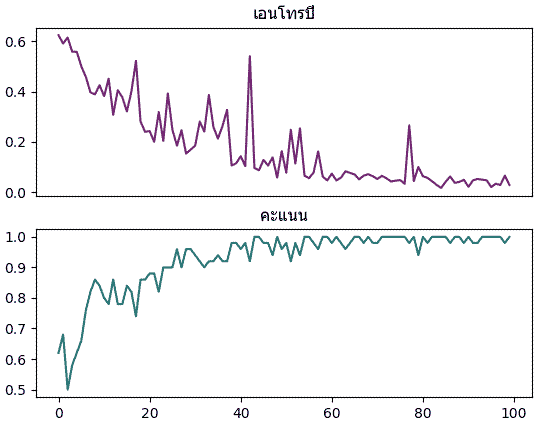
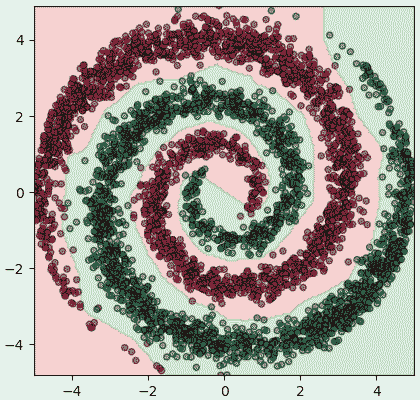
ผลที่ได้จะเห็นว่าเอนโทรปีไม่ได้ลดลงอย่างสม่ำเสมอแต่มีการขึ้นๆลงๆไม่แน่นอน เพราะแต่ละรอบสุ่มข้อมูลมาในลำดับที่ไม่ซ้ำกันทำให้ทิศทางการปรับพารามิเตอร์มีความไม่แน่นอนมากขึ้น แต่โดยแนวโน้มแล้วก็จะยังคงไปในทิศทางที่ลดลงเรื่อยๆ
>> อ่านต่อ บทที่ ๑๖
ในบทที่ผ่านๆมาเราใช้ข้อมูลที่มีในการฝึกโครงข่ายประสาทเทียมทีเดียวพร้อมกันทั้งหมด
แต่ในทางปฏิบัติแล้วเรานิยมแบ่งข้อมูลเป็นกลุ่มเล็กๆแล้วคำนวณทีละกลุ่ม วิธีการนี้เรียกว่ามินิแบตช์ (minibatch)
การใช้มินิแบตช์ในการเคลื่อนลงตามความชันก็ถือว่าเป็นการเคลื่อนลงตามความชันแบบสุ่ม (随机梯度下降法, stochastic gradient descent) เช่นเดียวกับการใช้ข้อมูลแค่ทีละตัว
การใช้ข้อมูลเป็นกลุ่มแบบนี้มีความแน่นอนมากกว่าใช้ข้อมูลทีละตัว เพราะทำให้ไม่ไวต่อข้อมูลตัวใดตัวหนึ่งมากไป
และจะดีกว่าการใช้ข้อมูลทั้งหมดทีเดียวในเรื่องของความเร็วด้วย ดังนั้นจึงสามารถทั้งรักษาความแน่นอนและเวลาในการคำนวณด้วย
นอกจากนี้ยังมีข้อดีอีกอย่าง นั่นคือลดโอกาสที่จะได้คำตอบที่เป็นแค่ค่าต่ำสุดสัมพัทธ์
ค่าต่ำสุดสัมพัทธ์คือค่าที่ดูแล้วต่ำที่สุดเมื่อเทียบกับบริเวณรอบๆ แต่จริงๆแล้วอาจยังมีจุดที่ต่ำกว่านั้นอยู่ไกลออกไป
ถ้าเราใช้ข้อมูลทั้งหมดทีเดียวค่าเสียหายก็จะมีอยู่ค่าเดียว ทิศทางของการปรับค่าก็จะค่อนข้างแน่นอน แบบนั้นถ้าเจอจุดต่ำสุดสัมพัทธ์ก่อนก็จะมุ่งไปทางนั้นและได้ตรงนั้นเป็นคำตอบ
แต่ถ้าเราเปลี่ยนกลุ่มข้อมูลที่พิจารณาไปเรื่อยๆค่าเสียหายที่คำนวณได้ก็จะเปลี่ยนไปในแต่ละครั้ง โอกาสที่จะเปลี่ยนทิศทางออกจากจุดสัมพัทธ์ตรงนั้นไปเจอจุดต่ำสุดอื่นก็จะมีมากขึ้น ดังนั้นจึงกลายเป็นว่าความไม่แน่นอนที่เกิดขึ้นนี้กลับเป็นผลดีมากกว่า
ด้วยเหตุนี้ทำให้ในทางปฏิบัติแล้วมินิแบตช์เป็นที่นิยมกว่า
ลองสร้างคลาสของโครงข่ายประสาทเทียมที่คล้ายกับที่ทำไปในบทที่ ๑๒ แต่เพิ่มการใช้มินิแบตช์ลงไป จะกลายเป็นแบบนี้ (อย่าลืมโหลดคลาสของชั้นต่างๆก่อนจาก >> unagi.py)
import numpy as np
import matplotlib.pyplot as plt
from unagi import Affin,Sigmoid,Sigmoid_entropy,Adam,Relu
class Prasat:
def __init__(self,m,eta,kratun='relu'):
m.append(1)
self.m = m
self.chan = []
for i in range(len(m)-1):
self.chan.append(Affin(m[i],m[i+1],np.sqrt(2./m[i])))
if(i<len(m)-2):
if(kratun=='relu'):
self.chan.append(Relu())
else:
self.chan.append(Sigmoid())
self.chan.append(Sigmoid_entropy())
self.opt = Adam(self.param(),eta=eta)
def rianru(self,X,z,n_thamsam,n_batch=50):
n = len(z)
self.entropy = []
self.khanaen = []
for o in range(n_thamsam):
lueak = np.random.permutation(n)
for i in range(0,n,n_batch):
Xb = X[lueak[i:i+n_batch]]
zb = z[lueak[i:i+n_batch]]
entropy = self.ha_entropy(Xb,zb)
entropy.phraeyon()
self.opt()
entropy,khanaen = self.ha_entropy(Xb,zb,ao_khanaen=1)
self.entropy.append(entropy.kha)
self.khanaen.append(khanaen)
def ha_entropy(self,X,z,ao_khanaen=0):
for c in self.chan[:-1]:
X = c(X)
if(ao_khanaen):
return self.chan[-1](X,z),((X.kha>=0).flatten()==z).mean()
return self.chan[-1](X,z)
def param(self):
p = []
for c in self.chan:
if(hasattr(c,'param')):
p.extend(c.param)
return p
def thamnai(self,X):
for c in self.chan[:-1]:
X = c(X)
return (X.kha>=0).flatten().astype(int)โดยรวมแล้วดูซับซ้อนขึ้นมา เพราะต้องเพิ่มวังวน for ด้านในมาเพื่อวนทำซ้ำเพื่อหยิบข้อมูลเป็นกลุ่มๆในแต่ละรอบ
ทุกรอบจะมีจำนวนข้อมูลเท่ากันหมดยกเว้นรอบสุดท้ายจะเป็นการเก็บเศษที่เหลืออยู่ ซึ่งอาจไม่ครบตามจำนวน
ในแต่ละรอบจะเปลี่ยนกลุ่ม เปลี่ยนลำดับการสุ่มทั้งหมด
นอกจากนี้เวลาคำนวณคะแนนจะไม่คำนวณในแต่ละรอบย่อย แต่จะรอให้ใช้ข้อมูลทั้งหมดครบแล้วคำนวณทั้งหมดพร้อมกันใหม่ทีเดียว จึงได้มีการปรับปรุงเมธอด .ha_entropy() ให้สามารถเลือกที่จะคำนวณค่าคะแนนไปด้วย ทั้งคะแนนและเอนโทรปีเป็นผลจากการคำนวณไปข้างหน้าเหมือนกัน แต่ต่างตรงขั้นตอนสุดท้าย ดังนั้นถ้าต้องการทั้งสองอย่างจึงควรคำนวณพร้อมกัน
สำหรับจำนวนต่อรอบนั้นโดยทั่วไปที่คนนิยมใช้กันมากคือเลขยกกำลังของสอง เช่น 64, 128, 256 สาเหตุไม่ใช่เพราะจะทำให้ผลลัพธ์ดีกว่า แต่เป็นเหตุผลในแง่ของความเร็ว เพราะคอมพิวเตอร์เก็บข้อมูลในรูปแบบของเลขฐานสองเป็นหลัก
ยังไงจำนวนต่อรอบต่างกันเล็กน้อยก็ไม่ได้มีผลกระทบต่อผลลัพธ์ ดังนั้นการเลือกค่าที่ทำให้คำนวณได้เร็วจึงกลายเป็นปัจจัยที่ถูกพิจารณาไป
ลองนำมาใช้จำแนกข้อมูลหน้าตาซับซ้อนแบบนี้
np.random.seed(7)
r = np.tile(np.sqrt(np.linspace(0.5,25,2000)),2)
t = np.random.normal(np.sqrt(r*50),0.5)
z = np.arange(2).repeat(2000)
t += z*np.pi
X = np.array([r*np.cos(t),r*np.sin(t)]).T
plt.scatter(X[:,0],X[:,1],50,c=z,alpha=0.1,edgecolor='k',cmap='RdYlGn')
plt.show()
ให้ทำการแบ่งเขตพร้อมทั้งแสดงค่าเอนโทรปีและคะแนนการทำนายด้วย
prasat = Prasat(m=[2,70],eta=0.005)
prasat.rianru(X,z,n_thamsam=100,n_batch=50)
plt.subplot(211,xticks=[])
plt.plot(prasat.entropy,'#772277')
plt.title(u'เอนโทรปี',family='Tahoma',size=12)
plt.subplot(212)
plt.plot(prasat.khanaen,'#227777')
plt.title(u'คะแนน',family='Tahoma',size=12)
plt.figure()
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),200),np.linspace(X[:,1].min(),X[:,1].max(),200))
mX = np.array([mx.ravel(),my.ravel()]).T
mz = prasat.thamnai(mX).reshape(200,-1)
plt.axes(aspect=1,xlim=(X[:,0].min(),X[:,0].max()),ylim=(X[:,1].min(),X[:,1].max()))
plt.contourf(mx,my,mz,cmap='RdYlGn',alpha=0.2)
plt.scatter(X[:,0],X[:,1],20,c=z,alpha=0.5,edgecolor='k',cmap='RdYlGn')
plt.show()

ผลที่ได้จะเห็นว่าเอนโทรปีไม่ได้ลดลงอย่างสม่ำเสมอแต่มีการขึ้นๆลงๆไม่แน่นอน เพราะแต่ละรอบสุ่มข้อมูลมาในลำดับที่ไม่ซ้ำกันทำให้ทิศทางการปรับพารามิเตอร์มีความไม่แน่นอนมากขึ้น แต่โดยแนวโน้มแล้วก็จะยังคงไปในทิศทางที่ลดลงเรื่อยๆ
>> อ่านต่อ บทที่ ๑๖
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy