manim บทที่ ๑๗: การใส่สูตรสมการทางคณิตศาสตร์
เขียนเมื่อ 2021/03/12 00:17
แก้ไขล่าสุด 2023/08/26 13:15
ต่อจาก บทที่ ๑๖
ในบทนี้จะพูดถึงการใส่สูตรสมการทางคณิตศาสตร์ต่างๆ
การสร้างสูตรสมการทางคณิตศาสตร์ด้วยคลาส Tex
คลาส Tex มีไว้สำหรับเขียนพวกสูตรสมการทางคณิตศาสตร์ขึ้นมาจากโค้ด LaTeX
อย่างไรก็ตาม ความสามารถตรงส่วนนี้มีความซับซ้อน และมีโอกาสเกิดบั๊กได้ง่าย คาดว่ายังน่าจะมีการเปลี่ยนแปลงอีกในอนาคต
สำหรับวิธีการเขียนโค้ด LaTeX นั้นจะไม่อธิบายในที่นี้ สามารถค้นตามเว็บเพื่อศึกษาเพิ่มเติมเอาเองได้
ขนาดของอักษรกำหนดได้ที่คีย์เวิร์ด font_size ส่วนสีกำหนดโดยคีย์เวิร์ด color
ตัวอย่าง ลองเขียนฟังก์ชันการแจกแจงเบตา
import manimlib as mnm
class Manimala(mnm.Scene):
def construct(self):
# ฟังก์ชันการแจกแจงเบตา
beta = mnm.Tex(r'f(\alpha,\beta) = \frac{x^{\alpha-1}(1-x)^{\beta-1} }{B(\alpha,\beta)}',font_size=96)
# แทนค่า α=2, β=3 ลงสมการ
beta23 = mnm.Tex(r'f(2,3) = \frac{x^{2-1}(1-x)^{3-1} }{B(2,3)}',font_size=96,color='#a4ff9a')
self.play(
mnm.Transform(beta,beta23),
run_time=1.5
)
self.wait(0.5)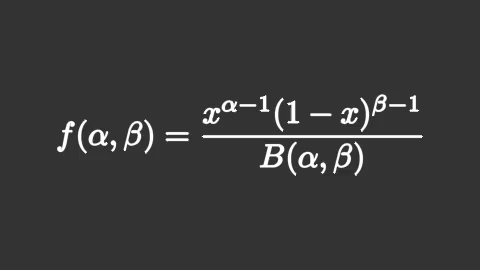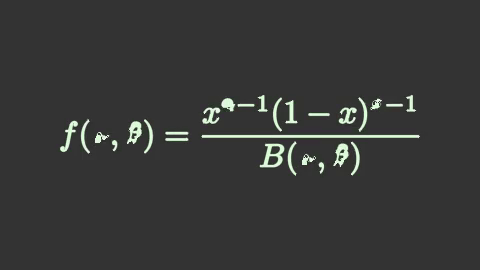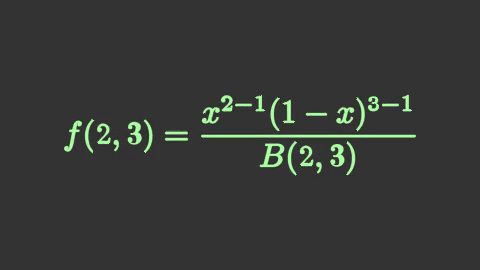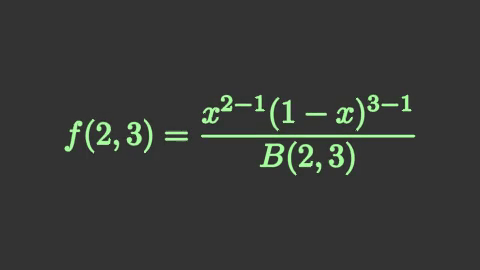
สามารถใส่ค่า fill_opacity กับ stroke_width เพื่อแสดงตัวอักษรเป็นโครงขอบได้
ตัวอย่าง เขียนฟังก์ชันการแจกแจงปัวซง
import manimlib as mnm
class Manimala(mnm.Scene):
def construct(self):
poisson = mnm.Tex(r'f(\lambda) = \frac{\lambda^x \exp(-\lambda)}{x!}',
font_size=144,
fill_opacity=0,
stroke_width=4)
poisson6 = mnm.Tex(r'f(6) = \frac{6^x \exp(-6)}{x!}',
font_size=144,
color='#9addff',
fill_opacity=0,
stroke_width=4)
self.play(
mnm.Transform(poisson,poisson6),
run_time=1.5
)
self.wait(0.5)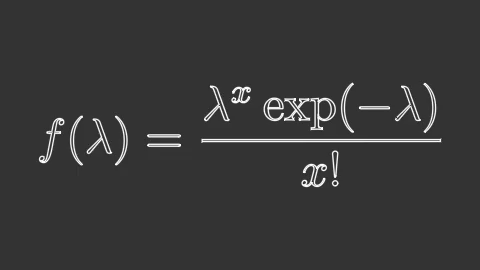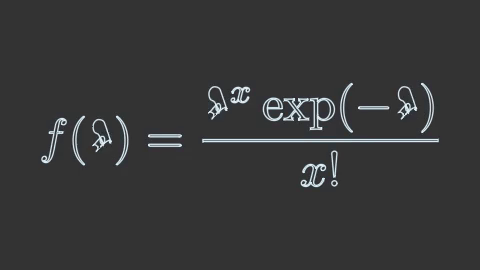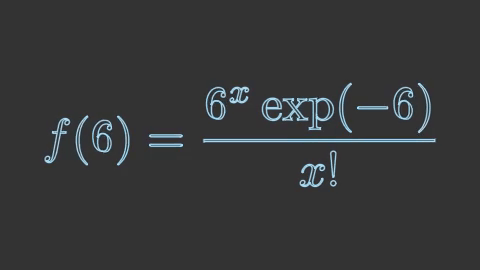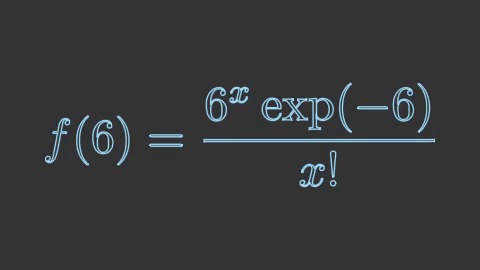
การแยกส่วนประกอบ
การสร้าง Tex ดังในตัวอย่างที่ผ่านมานั้น ส่วนประกอบทั้งหมดใน Tex จะถือว่าเป็นวัตถุตัวเดียวกันหมด ซึ่งถ้าหากไม่ใช่ว่าเราตั้งใจจะนำมาแยกส่วนเพื่อทำอะไรก็ไม่ได้มีปัญหาอะไร
แต่ในกรณีส่วนใหญ่นั้นเวลาแสดงภาพเคลื่อนไหวจำเป็นต้องทำการแยกส่วนประกอบต่างๆออกจากกันให้ชัดเจนไม่เช่นนั้นจะเกิดข้อผิดพลาดหรือไม่สามารถแสดงการเคลื่อนไหวที่ถูกต้องได้
การแยกส่วนประกอบภายใน Tex นั้นมีอยู่หลายวิธี โดยพื้นฐานแล้ววิธีที่ง่ายและแน่นอนที่สุดก็คือทำการแยกส่วนโดยใส่ไปทีละชิ้น
เช่นลองเขียนฟังก์ชันการแจกแจงแบร์นุลลี โดยทำการแยกส่วน อาจเขียนได้ดังนี้
mnm.Tex('f','(','p',')','=','p','^x','(','1','-','p)','^{1','-','x}')ซึ่งการที่ต้องมาเขียนแยกแบบนี้ก็ดูแล้วยุ่งยากและยังเข้าใจยากด้วย โดยทั่วไปจึงแนะนำให้ใช้วิธีการใส่ส่วนประกอบที่ต้องการแยกลงในคีย์เวิร์ด isolate แล้วส่วนประกอบที่ระบุทั้งหมดจะถูกแยกส่วนโดยอัตโนมัติ
ตัวอย่างการใช้
import manimlib as mnm
class Manimala(mnm.Scene):
def construct(self):
bernoulli = mnm.Tex(r'f(p) = p^x(1-p)^{1-x}',
isolate=['f','p','=','x','-','1'])
# แทนที่จะเขียนแยกส่วนเป็น
# bernoulli = mnm.Tex('f','(','p',')','=','p','^x','(','1','-','p)','^{1','-','x}')
bernoulli.set_color_by_gradient('#ff9add','#a9f2be')
self.play(
bernoulli.animate.set_width(13),
run_time=1.5
)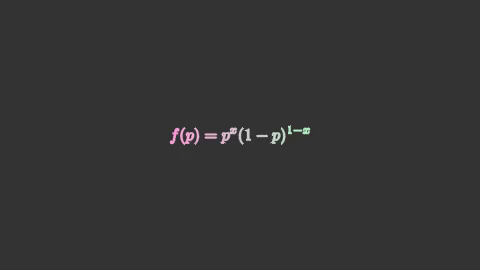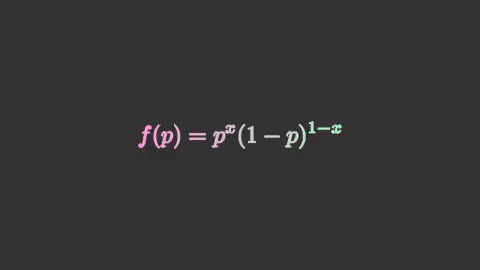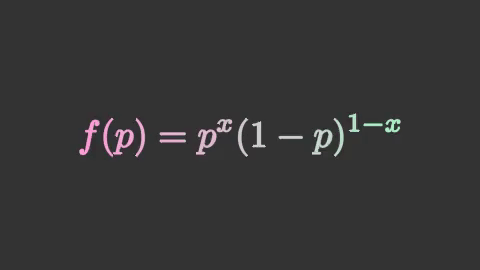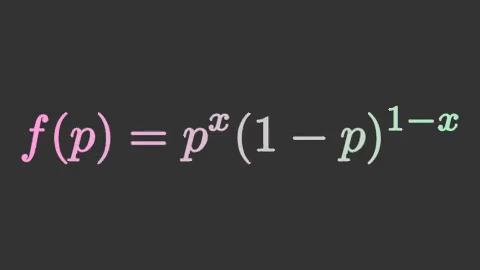
อนึ่ง ในตัวอย่างนี้ทำการแยกส่วนเพื่อให้สามารถใส่สีให้แต่ละส่วนแบบไล่สีด้วย .set_color_by_gradient() ได้ หากไม่แยกส่วนก็จะถือว่าทั้งก้อนเป็นวัตถุชิ้นเดียวและไม่สามารถเขียนให้ไล่สีได้
การแปลงส่วนประกอบด้วย TransformMatchingTex
ประโยชน์ของการแยกส่วนประกอบของวัตถุ Tex จะเห็นชัดเมื่อเวลาที่ทำการแปลงร่างวัตถุ โดยเฉพาะเมื่อใช้การแปลงด้วยคลาส TransformMatchingTex
TransformMatchingTex ใช้สำหรับแปลงร่าง Tex โดยเทียบส่วนประกอบที่เหมือนกันแล้วทำการย้ายค่าแทนที่ตามความเหมาะสม
ตัวอย่าง ลองสร้าง Tex ขึ้นมา ๒ ตัวโดยแยกส่วนประกอบหมดเหมือนกัน แล้วใช้ TransformMatchingTex ทำการแปลงดู
import manimlib as mnm
class Manimala(mnm.Scene):
def construct(self):
bernoulli = mnm.Tex(r'f(p) = p^x(1-p)^{1-x}',
isolate=['f','p','=','x','-','1'],
font_size=144)
bernoulli07 = mnm.Tex(r'f(0.7) = 0.7^x(1-0.7)^{1-x}',
isolate=['f','0.7','=','x','-','1'],
font_size=112,
color='#a9f2ee')
self.play(
mnm.TransformMatchingTex(bernoulli,
bernoulli07,
key_map={'p':'0.7'}),
run_time=1.5
)
self.wait(0.5)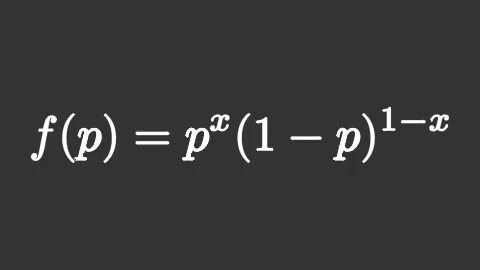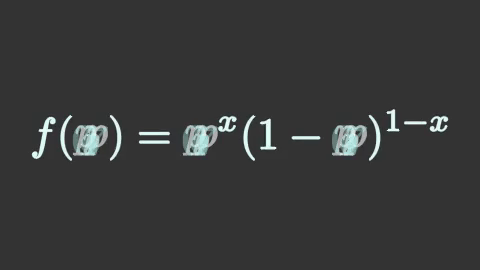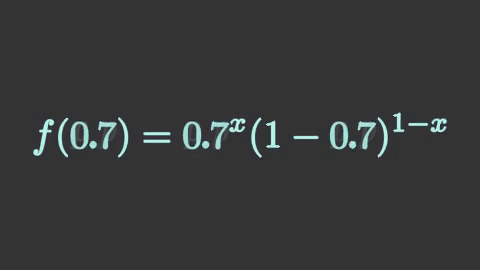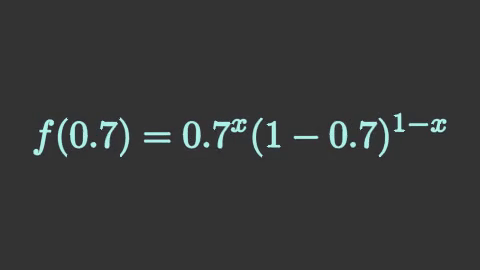
ผลที่ได้จะเห็นว่า 0.7 เข้าแทนที่ p ส่วนที่เหลือไม่มีการเปลี่ยนแปลงก็อยู่อย่างนั้น
การใส่ key_map={'p':'0.7'} นั้นเพื่อเป็นการบอกให้รู้ว่า p ให้แปลงเป็น 0.7
หากไม่ใส่ key_map ไว้ ผลที่ได้ก็จะกลายเป็นแค่ p หายไปแล้ว 0.7 ปรากฏขึ้นมาแทน แบบนี้
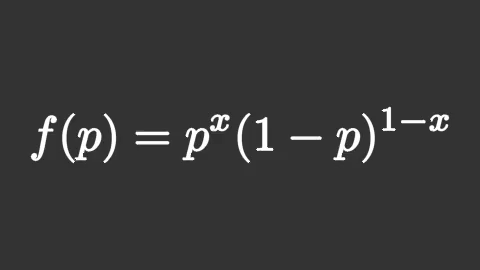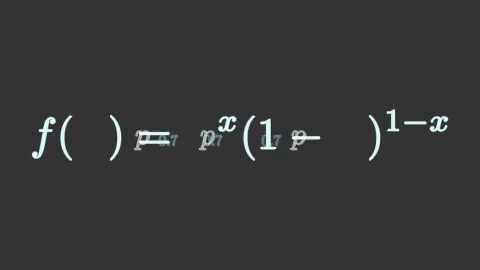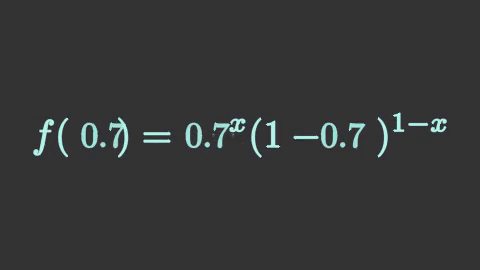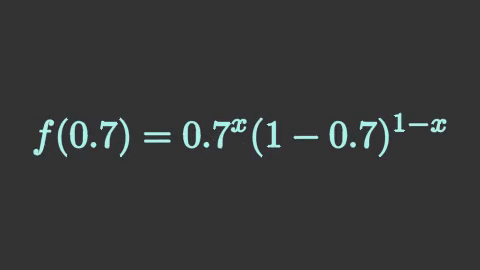
นอกจากนี้ หากไม่ได้ทำการแยกส่วนไว้ ผลที่ได้ก็จะต่างออกไปมาก หากลองทำเหมือนเดิมแต่เอาส่วน isolate ออกแล้วผลที่ได้จะเป็นแบบนี้
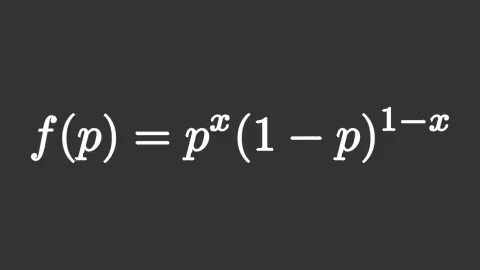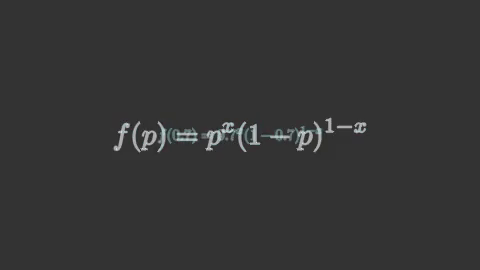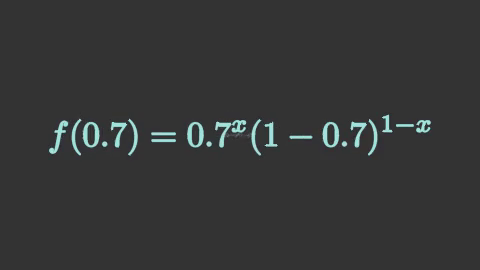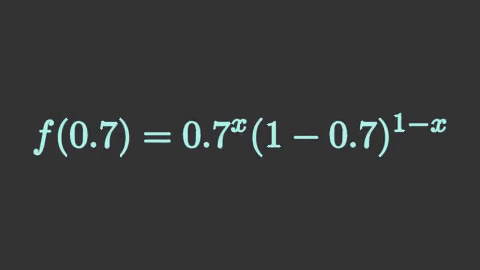
ซึ่งจะเห็นว่าเมื่อไม่มีการแยกส่วนก็จะแค่ทำให้ทั้งก้อนหายไปหมดแล้วแทนด้วยก้อนใหม่
ลองดูอีกตัวอย่างเพื่อให้เห็นภาพการใช้งานชัดขึ้น
import manimlib as mnm
class Manimala(mnm.Scene):
def construct(self):
tex1 = mnm.VGroup(mnm.Tex('n! =',
isolate=['n','!','='],
font_size=112),
mnm.Tex(r'n \times (n-1) \times \cdots \times 1',
isolate=['(','n-1',')','n',r'\times','1',r'\cdots'],
font_size=112))
tex1.arrange(mnm.RIGHT)
tex1.set_color('#cfa3d3')
tex2 = mnm.VGroup(mnm.Tex('6! =',
isolate=['6','!','='],
font_size=112),
mnm.Tex(r'6 \times 5 \times 4 \times 3 \times 2 \times 1',
isolate=['6','5','4','3','2','1',r'\times'],
font_size=112))
tex2.arrange(mnm.RIGHT)
tex2.set_color('#d0f2a9')
tex3 = mnm.VGroup(mnm.Tex('4! =',
isolate=['4','!','='],
font_size=112),
mnm.Tex(r'4 \times 3 \times 2 \times 1',
isolate=['4','3','2','1',r'\times'],
font_size=112))
tex3.arrange(mnm.RIGHT)
tex3.set_color('#d1d3a3')
vg = mnm.VGroup(tex1,tex3,tex2)
vg.arrange(mnm.DOWN,buff=1)
self.add(tex1)
self.play(
mnm.TransformMatchingTex(tex1[0].copy(),
tex2[0],
key_map={'n':'6'}),
mnm.TransformMatchingTex(tex1[1].copy(),
tex2[1],
key_map={'n':'6','n-1':'5'}),
run_time=1.25
)
self.play(
mnm.TransformMatchingTex(tex1[0].copy(),
tex3[0],
key_map={'n':'4'}),
mnm.TransformMatchingTex(tex1[1].copy(),
tex3[1],
key_map={'n':'4','n-1':'3'}),
run_time=1.25
)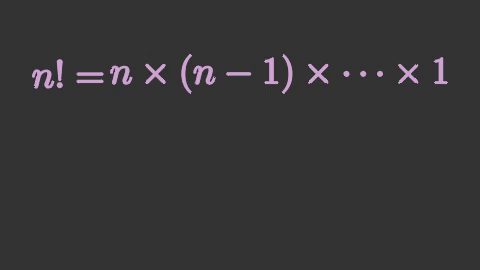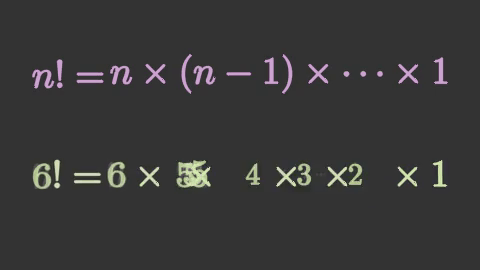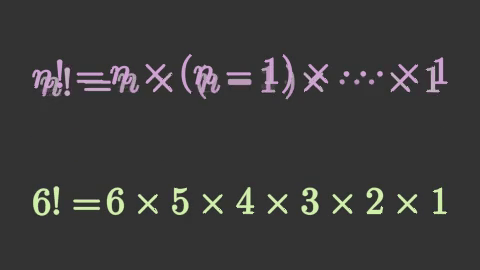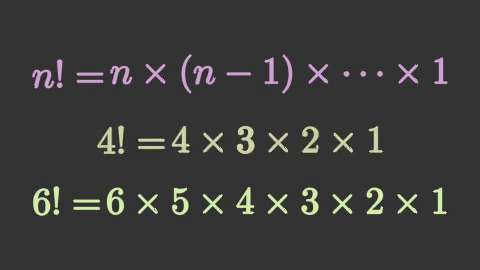
TexText
คลาส TexText ใช้เขียนข้อความพร้อมกับแทรกสูตรสมการทางคณิตศาสตร์ไปด้วย
เมื่อเทียบกับคลาส Text แล้ว ข้อได้เปรียบคือพิมพ์พวกสมการใส่ลงไปได้ แต่ข้อเสียคือวัตถุที่ได้จะมีลักษณะเหมือน Tex คือสร้างช้าและไม่สามารถใช้ภาษาไทยได้
ส่วนที่ต้องการใช้เป็นสูตรสมการทางคณิตศาสตร์ให้ล้อมด้วย $ $ ส่วนตัวหนังสือที่เป็นข้อความธรรมดาไม่ต้องใส่ $ $
ตัวอย่าง ลองเขียนฟังก์ชันการแจกแจงแบบเรขาคณิต และ การแจกแจงแบบทวินามเชิงลบ
import manimlib as mnm
class Manimala(mnm.Scene):
def construct(self):
tt = mnm.TexText(r'''Geometrinen jakauma \\
$p(1-p)^{x-1}$ \\
Negatiivinen binomijakauma \\
$C(x+r-1,x)(1-p)^rp^x$''',
color='#f2a9e0',
font_size=100)
self.play(
mnm.Write(tt),
run_time=1.25
)
self.wait(0.25)
Matrix
คลาส DecimalMatrix กับ IntegerMatrix ใช้สร้างเมทริกซ์ขึ้นมา โดย DecimalMatrix จะแสดงค่าเป็นเลขทศนิยม ส่วน IntegerMatrix จะแสดงค่าเป็นจำนวนเต็ม
ตัวอย่างการใช้
import manimlib as mnm
class Manimala(mnm.Scene):
def construct(self):
# ค่าในเมทริกซ์
matr = [[1.2,2.4,3.6],
[5,6.6,8.8]]
# เมทริกซ์เลขทศนิยม
matr1 = mnm.DecimalMatrix(matr)
matr1.set_color('#ddf2a9')
matr1.set_width(12)
# เมทริกซ์จำนวนเต็ม
matr2 = mnm.IntegerMatrix(matr)
matr2.set_color('#caa9f2')
matr2.set_width(12)
self.play(
mnm.Transform(matr1,matr2),
run_time=1.25
)
self.wait(0.25)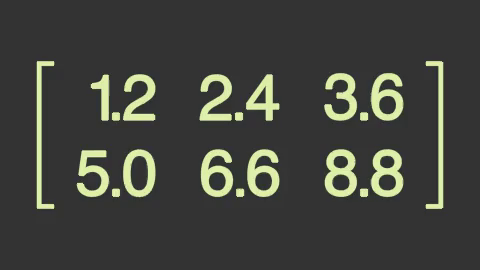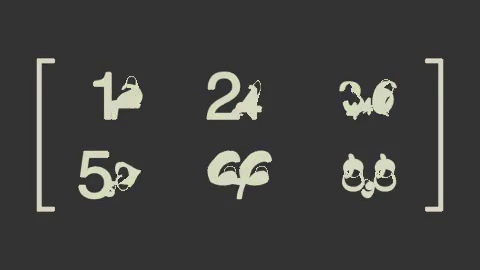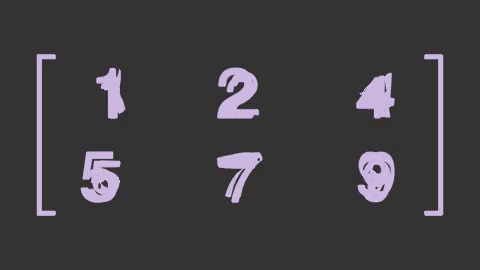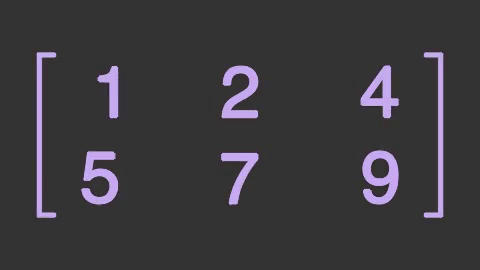
Brace
คลาส Brace ใช้สร้างปีกกาคร่อมวัตถุที่ต้องการ มักใช้เพื่อการอธิบายตัววัตถุนั้นๆ
การใช้ให้ใส่วัตถุที่ต้องการคร่อม แล้วก็ตามด้วยทิศที่จะวาง
ตัวอย่างเช่นลองสร้างปีกกาแล้วแสดงข้อความอธิบายส่วนจริงส่วนจินตภาพของจำนวนเชิงซ้อน
import manimlib as mnm
class Manimala(mnm.Scene):
def construct(self):
tex = mnm.Tex('7-x','+','3i+yi',font_size=180,color="#e3ebb8")
brace1 = mnm.Brace(tex[0],mnm.UP,color='#a3d3ba')
text1 = mnm.Text('ส่วนจริง',color='#a3d3ba',size=1.6)
text1.next_to(brace1,mnm.UP)
brace2 = mnm.Brace(tex[2],mnm.UP,color='#d3a3bf')
text2 = mnm.Text('ส่วนจินตภาพ',color='#d3a3bf',size=1.6)
text2.next_to(brace2,mnm.UP)
brace3 = mnm.Brace(tex,mnm.DOWN,color='#b8e3eb')
text3 = mnm.Text('จำนวนเชิงซ้อน',color='#b8e3eb',size=2)
text3.next_to(brace3,mnm.DOWN)
self.add(tex)
self.play(
mnm.ClockwiseTransform(tex[0].copy(),brace1),
mnm.CounterclockwiseTransform(tex[2].copy(),brace2),
mnm.FadeTransform(tex.copy(),brace3),
mnm.ShowCreation(text1),
mnm.Write(text2),
mnm.GrowFromCenter(text3),
run_time=1.1
)
self.wait(0.4)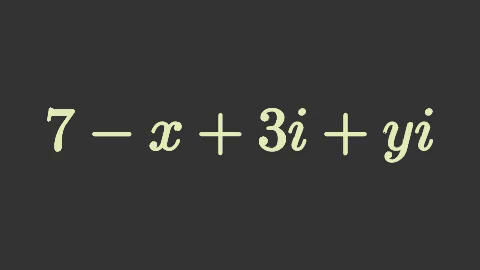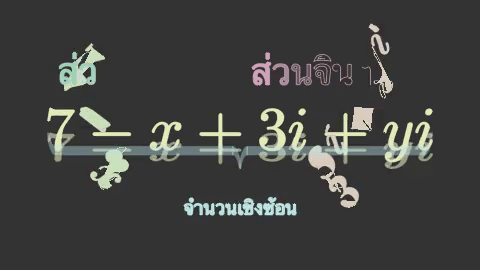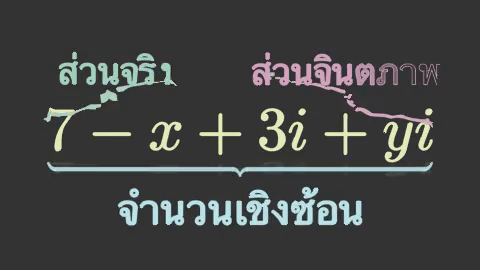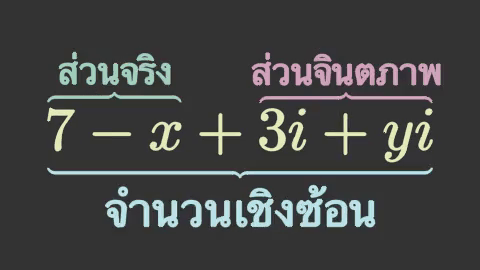
อ่านบทถัดไป >> บทที่ ๑๘