maya python เบื้องต้น บทที่ ๑๙: ความสัมพันธ์แบบพ่อแม่ลูก
เขียนเมื่อ 2016/03/11 01:59
แก้ไขล่าสุด 2021/09/28 16:42
ในบทที่แล้วพูด ถึงการนำวัตถุหลายๆชิ้นมารวมกลุ่มกันเพื่อให้สามารถควบคุมไปพร้อมๆกันได้ไป แล้ว ซึ่งในบทที่แล้วใช้คำสั่ง group() แต่ในบทนี้จะแนะนำอีกคำสั่งหนึ่งที่สามารถใช้ในการรวมกลุ่มวัตถุได้เช่นกัน แต่มีความต่างออกไป นั่นคือ parent()
parent() เป็นคำสั่งสำหรับรวมกลุ่มวัตถุโดยมีการกำหนดให้วัตถุอันหนึ่งเป็นตัวหลัก วัตถุที่ถูกตั้งให้เป็นตัวหลักนั้นจะถูกเรียกว่าเป็นพ่อแม่ (親, parent) ส่วนวัตถุอันอื่นๆจะเรียกว่าเป็นลูก (子, child) โดยระหว่างวัตถุที่เป็นพ่อแม่กับที่เป็นลูกนั้นจะมีความสัมพันธ์ในลักษณะที่ เรียกว่าความสัมพันธ์แบบพ่อแม่ลูก
เมื่อสร้างความสัมพันธ์แบบพ่อแม่ ลูกแล้ว เวลาที่เคลื่อนวัตถุที่เป็นตัวพ่อแม่แล้ววัตถุที่เป็นลูกก็จะเคลื่อนที่ตาม ไปด้วย แต่ถ้าเคลื่อนวัตถุที่เป็นลุกไปวัตถุที่เป็นพ่อแม่จะไม่เคลื่อนตามไป
ซึ่ง จะเห็นว่าการรวมกลุ่มในลักษณะเช่นนี้ต่างจาก group() ซึ่งทุกตัวจะมีฐานะเท่าเทียมกันหมด แต่การใช้ parent() นั้นวัตถุจะมีฐานะไม่เท่าเทียมกัน คือจะมีตัวหนึ่งที่เป็นตัวหลักเสมอ
การใช้ฟังก์ชัน parent() คือให้ใส่อาร์กิวเมนต์เป็นชื่อวัตถุทั้งหมดที่ต้องการรวม โดยให้ตัวที่ต้องการให้เป็นพ่อแม่อยู่ลำดับท้ายสุด
ปกติ ถ้าหากว่ามีวัตถุชิ้นหนึ่งเป็นหลักใหญ่สำคัญกว่าชิ้นอื่น แล้วชิ้นอื่นมักต้องเคลื่อนที่ตามมัน กรณีแบบนี้มักจะใช้ความสัมพันธ์แบบพ่อแม่ลูกมากกว่าที่จะเป็นแบบรวมกลุ่มกัน ธรรมดา
ตัวอย่าง ลองสร้างเต่ากระดองหกเหลี่ยมแบบง่ายๆขึ้นมาสักตัวโดยประกอบด้วย หัว, หาง, ขาทั้งสี่ ทั้งหมด ๖ ชิ้นนี้สร้างขึ้นมาแล้วเอาไปผูกติดกับกระดอง จากนั้นสร้างลูกตาสองอันแล้วมาผูกติดกับส่วนหัวอีกที
ทำแบบนี้แล้วก็จะได้เต่ามาตัวหนึ่ง ซึ่งตอนนี้ชิ้นส่วนยังแยกกันอยู่ ยังไม่ได้ทำการผูกติดสร้างความสัมพันธ์ระหว่างวัตถุ

จากนั้นลอง
แบบนี้ตาซ้ายและตาขวาก็จะมาผูกติดกับหัว
ดูภายนอกแล้วอาจเห็นว่าไม่มีอะไรเปลี่ยนแปลงไปแต่ถ้าดูในเอาต์ไลเนอร์ก็จะเห็นว่าโหนดของตาซ้ายและขวาเข้าไปอยู่ด้านล่างส่วนหัว
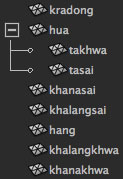
ถ้ากดที่ส่วนหัวดู mc.select('hua') ส่วนตาทั้งสองข้างก็จะถูกเลือกไปด้วย
และนอกจากนี้หากดูที่แชนเนลบ็อกซ์จะเห็นความเปลี่ยนแปลง โดยที่มาตราส่วนกลายเป็น (0.714,1.25,0.417) ทั้งๆที่ตอนแรกไม่ได้มีการไปปรับมาตราส่วนตรงส่วนตาเลย
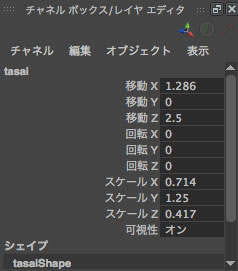
ที่เป็นแบบ นี้เพราะว่าวัตถุที่เป็นลูกจะถูกปรับค่าให้เป็นสัมพัทธ์เทียบกับวัตถุที่ เป็นพ่อแม่ ในที่นี้ส่วนหัวอยู่ในสภาวะที่ถูกปรับมาตราส่วนเป็น (1.4,0.8,2.4) มาตั้งแต่แรก ดังนั้นตาทั้งสองข้างก็เลยถูกปรับมาตราส่วนให้เป็นไปในทางตรงกันข้ามเพื่อ ให้สัมพันธ์กัน จะเห็นว่าเอา 1 มาหาร (0.714,1.25,0.417) ก็จะได้ (1.4,0.8,2.4)
ตำแหน่งก็ถูกเปลี่ยนให้สัมพันธ์เช่นกัน โดยตอนแรกตาซ้ายถูกวางไว้ที่ (1.8,0,16) แต่ตอนนี้กลายเป็น (1.286,0,2.5) โดยจะเห็นว่าตำแหน่งในแกน x คือ 1.286 นั้นได้จากการเอาตำแหน่งเดิม 1.8 หารด้วยมาตราส่วน 1.4 ส่วน ตำแหน่งในแกน z คือ 2.5 นั้นได้จากการเอาตำแหน่งเดิม 16 ลบด้วยตำแหน่งของส่วนหัว 10 แล้วหารด้วยมาตราส่วน 2.4
โดยปกติแล้วการใช้ parent() จะทำให้เกิดการเปลี่ยนแปลงในลักษณะนี้เสมอ แต่หากใส่แฟล็ก r (relative) ลงไปเป็น r=1 จะให้ผลที่ตรงกันข้ามกัน นั่นคือค่ามาตราส่วนและตำแหน่งที่อ่านได้จะไม่เปลี่ยนแปลง แต่จะไปเปลี่ยนแปลงสิ่งที่ปรากฏแทน เพราะค่าตรงนั้นกลายเป็นค่าสัมพัทธ์เทียบกับวัตถุพ่อแม่ไปตรงๆทั้งๆที่ไม่มี การปรับ
หลังจากที่รวมตาเข้ากับหัวแล้ว จากนั้นต่อไปก็จะรวมส่วนหัวรวมทั้งส่วนขาและหางเข้ากับกระดอง คราวนี้ในอาร์กิวเมนต์ใส่ลิสต์ที่เก็บชื่อของทั้ง ๖ ส่วน ซึ่งถูกสร้างไว้แต่แรกแล้ว ตามด้วยกระดอง
เท่านี้วัตถุทั้งหมดก็ถูกผูกรวมเข้าด้วยกันโดยมีกระดองเป็นส่วนหลักแล้ว
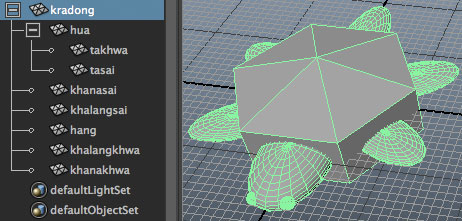
ถ้าหากกดเลือกที่ตัวกระดอง
ชิ้นส่วนอื่นก็จะถูกเลือกไปพร้อมกัน และถ้าหากเลื่อนตำแหน่งกระดองไปส่วนอื่นก็จะเลื่อนตาม ถ้าหมุนก็หมุนตาม ถ้าขยายก็ขยายตาม หรือถ้าลบก็จะหายไปหมด ในขณะที่ถ้าเลือกส่วนอื่นก็จะไปแค่ตัวนั้น กระดองหรือส่วนอื่นไม่เลื่อนตาม
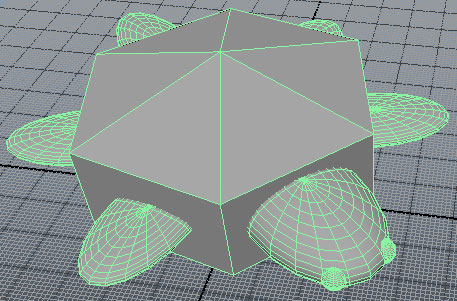
ตอนที่เลื่อนตำแหน่งกระดองไปแล้วส่วนอื่นก็เลื่อนตามไปด้วยนั้น ค่าความเปลี่ยนแปลงนั้นเกิดขึ้นแค่ที่ตัวกระดอง เช่นลองเลื่อนกระดองขึ้นไปด้านบน แล้วหมุน แล้วก็ขยาย
การยกเลิกความสัมพันธ์แบบพ่อแม่ลูกสามารถทำได้โดยใช้ฟังก์ชัน parent() โดยใส่อาร์กิวเมนต์เป็นวัตถุที่ต้องการแยกตัวออก แล้วใส่แฟล็ก w (world)
เช่น ลองแยกส่วนหัวออกจากกระดอง
พอลองแยกดูแล้วจะพบว่าค่าองค์ประกอบทั้งหมดที่เปลี่ยนแปลงไปจะถูกคำนวณแล้วใส่ลงในวัตถุส่วนหัว
การสร้างความสัมพันธ์แบบพ่อแม่ลูกนั้นใช้ประโยชน์ได้ดีเวลาทำภาพเคลื่อนไหว เช่นถ้ามีวัตถุหนึ่งเป็นหลักแล้วของอย่างอื่นเคลื่อนตามไปด้วย
เช่นถ้านำเต่าที่สร้างขึ้นมานี้ไปยืนบนอะไรที่เคลื่อนที่อยู่ มันก็ควรจะต้องเคลื่อนที่ตามนั้น
ขอยกตัวอย่างโดยนำเต่าไปวางบนเมฆวิเศษซึ่งกำลังเคลื่อนที่
เมฆวิเศษ (筋斗雲, kintoun) เป็นอุปกรณ์พิเศษจากการ์ตูนเรื่องดรากอนบอล เป็นเมฆเล็กๆที่คนสามารถขึ้นไปขี่และควบคุมได้ แต่คนที่จะขี่ได้ต้องมีจิตใจที่บริสุทธิ์เท่านั้น ดังนั้นผู้เฒ่าเต่าจึงขี่ไม่ได้
ลองสมมุติ สถานการณ์ว่าเต่าของเรากำลังขี่เมฆวิเศษอยู่ เมฆเคลื่อนไปข้างหน้าเรื่อยๆ แต่อยู่ดีๆก็เกิดคิดอะไรอกุศลขึ้นมาทำให้ใจไม่บริสุทธิ์ก็เลยร่วงตกจากเมฆ
ปกติ แล้ววัตถุที่กำลังเคลื่อนที่อยู่จะมีความเฉื่อย ดังนั้นแม้ว่าจะร่วงตกจากวัตถุที่เคลื่อนที่ไปแล้ววัตถุที่ร่วงก็ยังคง เคลื่อนที่ต่อไปด้วยความเร็วเท่าเดิม เพียงแต่มีความเร็วในแนวดิ่งเพิ่มขึ้นมาเท่านั้น ในกรณีแบบนี้ก็สามารถใช้ parent() เพื่อช่วยให้ง่ายได้

นอกจากนี้ parent() ยังอาจใช้แทน group() โดยแทนที่จะสร้างกลุ่มขึ้นมาเราก็นำวัตถุทั้งหมดไปผูกติดไว้กับอะไรสักอย่าง แทน ซึ่งอาจจะสะดวกกว่าการรวมกลุ่มเฉยๆตรงที่กลุ่มไม่ใช่วัตถุที่มองเห็นได้ เวลาจะเลือกต้องมาเลือกใน outliner ซึ่งบางทีอาจไม่สะดวก
ดังนั้นเราอาจใช้วิธีนำวัตถุมาผูกติดกับวัตถุชนิดหนึ่งที่สามารถมองเห็นได้ในฉาก แต่ไม่มีตัวตนอยู่จริง เป็นเพียงเสมือนเครื่องทำสัญลักษณ์เท่านั้น วัตถุนั้นเรียกว่าโลเคเตอร์ (locator) สามารถสร้างขึ้นมาได้โดยฟังก์ชัน spaceLocator()
การสร้างให้ใส่ตำแหน่งพิกัดที่ต้องการให้ตั้งอยู่ลงในแฟล็ก p (position) และก็สามารถตั้งชื่อด้วยแฟล็ก n (name)
๓ บรรทัดสุดท้ายเป็นการปรับขนาดปรากฏของโลเคเตอร์ เพราะขนาดเดิมอาจเล็กไปทำให้สังเกตได้ยาก โดยสามารถไปปรับได้ที่ค่าองค์ประกอบที่อยู่ภายในโหนดที่มีชื่อเป็นชื่อโลเค เตอร์ที่ตั้งบวกด้วย Shape
ค่าขนาดกำหนดโดย lsx (localScaleX) lsy (localScaleY) lsz (localScaleZ)
อีกอย่างที่อาจปรับได้ก็คือตำแหน่ง กำหนดโดย lpx (localPositionX) lpy (localPositionY) lpz (localPositionZ)
ทั้งการปรับขนาดและการเลื่อนแบบนี้จะไม่มีผลต่อวัตถุที่อยู่ภายในเพราะเป็นเพียงองค์ประกอบภายในของตัวโลเคเตอร์เอง
ไม่ว่าโลเคเตอร์จะมีขนาดใหญ่แค่ไหนหรืออยู่ตรงไหนก็ตามเวลาที่เรนเดอร์ภาพออกมาก็จะมองไม่เห็น เพราะเป็นแค่วัตถุสมมุติเท่านั้น
จะใช้ spaceLocator() คู่กับ parent() หรือจะใช้ group() ก็แล้วแต่ความสะดวก
อ้างอิง
parent() เป็นคำสั่งสำหรับรวมกลุ่มวัตถุโดยมีการกำหนดให้วัตถุอันหนึ่งเป็นตัวหลัก วัตถุที่ถูกตั้งให้เป็นตัวหลักนั้นจะถูกเรียกว่าเป็นพ่อแม่ (親, parent) ส่วนวัตถุอันอื่นๆจะเรียกว่าเป็นลูก (子, child) โดยระหว่างวัตถุที่เป็นพ่อแม่กับที่เป็นลูกนั้นจะมีความสัมพันธ์ในลักษณะที่ เรียกว่าความสัมพันธ์แบบพ่อแม่ลูก
เมื่อสร้างความสัมพันธ์แบบพ่อแม่ ลูกแล้ว เวลาที่เคลื่อนวัตถุที่เป็นตัวพ่อแม่แล้ววัตถุที่เป็นลูกก็จะเคลื่อนที่ตาม ไปด้วย แต่ถ้าเคลื่อนวัตถุที่เป็นลุกไปวัตถุที่เป็นพ่อแม่จะไม่เคลื่อนตามไป
ซึ่ง จะเห็นว่าการรวมกลุ่มในลักษณะเช่นนี้ต่างจาก group() ซึ่งทุกตัวจะมีฐานะเท่าเทียมกันหมด แต่การใช้ parent() นั้นวัตถุจะมีฐานะไม่เท่าเทียมกัน คือจะมีตัวหนึ่งที่เป็นตัวหลักเสมอ
การใช้ฟังก์ชัน parent() คือให้ใส่อาร์กิวเมนต์เป็นชื่อวัตถุทั้งหมดที่ต้องการรวม โดยให้ตัวที่ต้องการให้เป็นพ่อแม่อยู่ลำดับท้ายสุด
ปกติ ถ้าหากว่ามีวัตถุชิ้นหนึ่งเป็นหลักใหญ่สำคัญกว่าชิ้นอื่น แล้วชิ้นอื่นมักต้องเคลื่อนที่ตามมัน กรณีแบบนี้มักจะใช้ความสัมพันธ์แบบพ่อแม่ลูกมากกว่าที่จะเป็นแบบรวมกลุ่มกัน ธรรมดา
ตัวอย่าง ลองสร้างเต่ากระดองหกเหลี่ยมแบบง่ายๆขึ้นมาสักตัวโดยประกอบด้วย หัว, หาง, ขาทั้งสี่ ทั้งหมด ๖ ชิ้นนี้สร้างขึ้นมาแล้วเอาไปผูกติดกับกระดอง จากนั้นสร้างลูกตาสองอันแล้วมาผูกติดกับส่วนหัวอีกที
mc.polySphere(r=13,sx=6,sy=3,n='kradong') # ส่วนกระดอง
mc.scale(1,0.5,1)
huahangkha = ['hua','khanasai','khalangsai','hang','khalangkhwa','khanakhwa'] # ลิสต์เก็บชื่อของส่วนประกอบหัวหางขา
for i in range(6):
mc.polySphere(r=3,n=huahangkha[i])
if(i==0):
mc.scale(1.4,0.8,2.4) # สำหรับส่วนหัว
elif(i==3):
mc.scale(1,0.5,3) # สำหรับส่วนหาง
else:
mc.scale(1,0.3,2) # สำหรับขาทั้ง ๔
mc.move(0,0,10)
mc.rotate(0,60*i,0,p=[0,0,0]) # หมุนไปไว้คนละมุม
mc.polySphere(r=0.8,n='tasai') # ตาซ้าย
mc.move(1.8,0,16)
mc.polySphere(r=0.8,n='takhwa') # ตาขวา
mc.move(-1.8,0,16)
mc.scale(1,0.5,1)
huahangkha = ['hua','khanasai','khalangsai','hang','khalangkhwa','khanakhwa'] # ลิสต์เก็บชื่อของส่วนประกอบหัวหางขา
for i in range(6):
mc.polySphere(r=3,n=huahangkha[i])
if(i==0):
mc.scale(1.4,0.8,2.4) # สำหรับส่วนหัว
elif(i==3):
mc.scale(1,0.5,3) # สำหรับส่วนหาง
else:
mc.scale(1,0.3,2) # สำหรับขาทั้ง ๔
mc.move(0,0,10)
mc.rotate(0,60*i,0,p=[0,0,0]) # หมุนไปไว้คนละมุม
mc.polySphere(r=0.8,n='tasai') # ตาซ้าย
mc.move(1.8,0,16)
mc.polySphere(r=0.8,n='takhwa') # ตาขวา
mc.move(-1.8,0,16)
ทำแบบนี้แล้วก็จะได้เต่ามาตัวหนึ่ง ซึ่งตอนนี้ชิ้นส่วนยังแยกกันอยู่ ยังไม่ได้ทำการผูกติดสร้างความสัมพันธ์ระหว่างวัตถุ

จากนั้นลอง
mc.parent('takhwa','tasai','hua')
แบบนี้ตาซ้ายและตาขวาก็จะมาผูกติดกับหัว
ดูภายนอกแล้วอาจเห็นว่าไม่มีอะไรเปลี่ยนแปลงไปแต่ถ้าดูในเอาต์ไลเนอร์ก็จะเห็นว่าโหนดของตาซ้ายและขวาเข้าไปอยู่ด้านล่างส่วนหัว

ถ้ากดที่ส่วนหัวดู mc.select('hua') ส่วนตาทั้งสองข้างก็จะถูกเลือกไปด้วย
และนอกจากนี้หากดูที่แชนเนลบ็อกซ์จะเห็นความเปลี่ยนแปลง โดยที่มาตราส่วนกลายเป็น (0.714,1.25,0.417) ทั้งๆที่ตอนแรกไม่ได้มีการไปปรับมาตราส่วนตรงส่วนตาเลย

ที่เป็นแบบ นี้เพราะว่าวัตถุที่เป็นลูกจะถูกปรับค่าให้เป็นสัมพัทธ์เทียบกับวัตถุที่ เป็นพ่อแม่ ในที่นี้ส่วนหัวอยู่ในสภาวะที่ถูกปรับมาตราส่วนเป็น (1.4,0.8,2.4) มาตั้งแต่แรก ดังนั้นตาทั้งสองข้างก็เลยถูกปรับมาตราส่วนให้เป็นไปในทางตรงกันข้ามเพื่อ ให้สัมพันธ์กัน จะเห็นว่าเอา 1 มาหาร (0.714,1.25,0.417) ก็จะได้ (1.4,0.8,2.4)
ตำแหน่งก็ถูกเปลี่ยนให้สัมพันธ์เช่นกัน โดยตอนแรกตาซ้ายถูกวางไว้ที่ (1.8,0,16) แต่ตอนนี้กลายเป็น (1.286,0,2.5) โดยจะเห็นว่าตำแหน่งในแกน x คือ 1.286 นั้นได้จากการเอาตำแหน่งเดิม 1.8 หารด้วยมาตราส่วน 1.4 ส่วน ตำแหน่งในแกน z คือ 2.5 นั้นได้จากการเอาตำแหน่งเดิม 16 ลบด้วยตำแหน่งของส่วนหัว 10 แล้วหารด้วยมาตราส่วน 2.4
โดยปกติแล้วการใช้ parent() จะทำให้เกิดการเปลี่ยนแปลงในลักษณะนี้เสมอ แต่หากใส่แฟล็ก r (relative) ลงไปเป็น r=1 จะให้ผลที่ตรงกันข้ามกัน นั่นคือค่ามาตราส่วนและตำแหน่งที่อ่านได้จะไม่เปลี่ยนแปลง แต่จะไปเปลี่ยนแปลงสิ่งที่ปรากฏแทน เพราะค่าตรงนั้นกลายเป็นค่าสัมพัทธ์เทียบกับวัตถุพ่อแม่ไปตรงๆทั้งๆที่ไม่มี การปรับ
หลังจากที่รวมตาเข้ากับหัวแล้ว จากนั้นต่อไปก็จะรวมส่วนหัวรวมทั้งส่วนขาและหางเข้ากับกระดอง คราวนี้ในอาร์กิวเมนต์ใส่ลิสต์ที่เก็บชื่อของทั้ง ๖ ส่วน ซึ่งถูกสร้างไว้แต่แรกแล้ว ตามด้วยกระดอง
mc.parent(huahangkha,'kradong')
เท่านี้วัตถุทั้งหมดก็ถูกผูกรวมเข้าด้วยกันโดยมีกระดองเป็นส่วนหลักแล้ว
ถ้าหากกดเลือกที่ตัวกระดอง
mc.select('kradong')
ชิ้นส่วนอื่นก็จะถูกเลือกไปพร้อมกัน และถ้าหากเลื่อนตำแหน่งกระดองไปส่วนอื่นก็จะเลื่อนตาม ถ้าหมุนก็หมุนตาม ถ้าขยายก็ขยายตาม หรือถ้าลบก็จะหายไปหมด ในขณะที่ถ้าเลือกส่วนอื่นก็จะไปแค่ตัวนั้น กระดองหรือส่วนอื่นไม่เลื่อนตาม

ตอนที่เลื่อนตำแหน่งกระดองไปแล้วส่วนอื่นก็เลื่อนตามไปด้วยนั้น ค่าความเปลี่ยนแปลงนั้นเกิดขึ้นแค่ที่ตัวกระดอง เช่นลองเลื่อนกระดองขึ้นไปด้านบน แล้วหมุน แล้วก็ขยาย
mc.move(0,20,0,'kradong')
mc.rotate(0,45,0,'kradong')
mc.scale(3,3,3,'kradong',r=1)
จะพบว่าส่วนต่างๆเปลี่ยนขนาดหรือตำแหน่งไปตามกระดองแต่พอดูค่าองค์ประกอบต่างๆในตัววัตถุที่เป็นลูกจะเห็นว่าไม่มีการเปลี่ยนแปลงจริงๆmc.rotate(0,45,0,'kradong')
mc.scale(3,3,3,'kradong',r=1)

การยกเลิกความสัมพันธ์แบบพ่อแม่ลูกสามารถทำได้โดยใช้ฟังก์ชัน parent() โดยใส่อาร์กิวเมนต์เป็นวัตถุที่ต้องการแยกตัวออก แล้วใส่แฟล็ก w (world)
เช่น ลองแยกส่วนหัวออกจากกระดอง
mc.parent('hua','kradong',w=1)
พอลองแยกดูแล้วจะพบว่าค่าองค์ประกอบทั้งหมดที่เปลี่ยนแปลงไปจะถูกคำนวณแล้วใส่ลงในวัตถุส่วนหัว
การสร้างความสัมพันธ์แบบพ่อแม่ลูกนั้นใช้ประโยชน์ได้ดีเวลาทำภาพเคลื่อนไหว เช่นถ้ามีวัตถุหนึ่งเป็นหลักแล้วของอย่างอื่นเคลื่อนตามไปด้วย
เช่นถ้านำเต่าที่สร้างขึ้นมานี้ไปยืนบนอะไรที่เคลื่อนที่อยู่ มันก็ควรจะต้องเคลื่อนที่ตามนั้น
ขอยกตัวอย่างโดยนำเต่าไปวางบนเมฆวิเศษซึ่งกำลังเคลื่อนที่
เมฆวิเศษ (筋斗雲, kintoun) เป็นอุปกรณ์พิเศษจากการ์ตูนเรื่องดรากอนบอล เป็นเมฆเล็กๆที่คนสามารถขึ้นไปขี่และควบคุมได้ แต่คนที่จะขี่ได้ต้องมีจิตใจที่บริสุทธิ์เท่านั้น ดังนั้นผู้เฒ่าเต่าจึงขี่ไม่ได้
ลองสมมุติ สถานการณ์ว่าเต่าของเรากำลังขี่เมฆวิเศษอยู่ เมฆเคลื่อนไปข้างหน้าเรื่อยๆ แต่อยู่ดีๆก็เกิดคิดอะไรอกุศลขึ้นมาทำให้ใจไม่บริสุทธิ์ก็เลยร่วงตกจากเมฆ
ปกติ แล้ววัตถุที่กำลังเคลื่อนที่อยู่จะมีความเฉื่อย ดังนั้นแม้ว่าจะร่วงตกจากวัตถุที่เคลื่อนที่ไปแล้ววัตถุที่ร่วงก็ยังคง เคลื่อนที่ต่อไปด้วยความเร็วเท่าเดิม เพียงแต่มีความเร็วในแนวดิ่งเพิ่มขึ้นมาเท่านั้น ในกรณีแบบนี้ก็สามารถใช้ parent() เพื่อช่วยให้ง่ายได้
import math
mc.polySphere(r=15,n='mekwiset') # สร้างเมฆวิเศษก้อนตรงกลาง
mc.scale(1,0.4,1) # บี้ให้แบน
for i in range(6):
mc.polySphere(r=8,n='mek%d'%(i+1)) # สร้างเมฆ ๖ ก้อนรอบๆ
mc.move(0,0,15) # ย้ายไปให้ห่างจากใจกลาง
mc.scale(1,0.7,1) # บี้ให้แบน
mc.rotate(0,60*i,0,p=[0,0,0]) # หมุนไปคนละมุม
mc.parent(['mek%d'%(i+1) for i in range(6)],['mekwiset']) # นำมาผูกรวมกับก้อนกลาง
# สร้างเต่า
mc.polySphere(r=13,sx=6,sy=3,n='kradong')
mc.scale(1,0.5,1)
huahangkha = ['hua','khanasai','khalangsai','hang','khalangkhwa','khanakhwa']
for i in range(6):
mc.polySphere(r=3,n=huahangkha[i])
if(i==0):
mc.scale(1.4,0.8,2.4)
elif(i==3):
mc.scale(1,0.5,3)
else:
mc.scale(1,0.3,2)
mc.move(0,0,10)
mc.rotate(0,60*i,0,p=[0,0,0])
mc.polySphere(r=0.8,n='tasai')
mc.move(1.8,0,16)
mc.polySphere(r=0.8,n='takhwa')
mc.move(-1.8,0,16)
mc.parent('takhwa','tasai','hua')
mc.parent(huahangkha,'kradong')
mc.parent('kradong','mekwiset')
# ตั้งเอ็กซ์เพรชชัน
mc.expression(o='mekwiset',s='tz=30*time') # เมฆเคลื่อนไปข้างหน้า
mc.expression(o='khanasai',s='rx=40*sin(time*%d)'%math.pi) # ขาทั้ง ๔ ขยับไปเรื่อยๆ
mc.expression(o='khalangsai',s='rx=40*cos(time*%d)'%math.pi)
mc.expression(o='khalangkhwa',s='rx=-40*sin(time*%d)'%math.pi)
mc.expression(o='khanakhwa',s='rx=-40*cos(time*%d)'%math.pi)
mc.expression(o='hua',s='tz=5+5*sin(time*%d/5)'%math.pi) # ส่วนหัวก็ขยับ
mc.expression(o='kradong',s='if(time>2.5) ty=16-pow(time-2.5,2)*20; else ty=16') # พอถึงเวลา 2.5 เต่าเริ่มร่วงจากเมฆ
mc.polySphere(r=15,n='mekwiset') # สร้างเมฆวิเศษก้อนตรงกลาง
mc.scale(1,0.4,1) # บี้ให้แบน
for i in range(6):
mc.polySphere(r=8,n='mek%d'%(i+1)) # สร้างเมฆ ๖ ก้อนรอบๆ
mc.move(0,0,15) # ย้ายไปให้ห่างจากใจกลาง
mc.scale(1,0.7,1) # บี้ให้แบน
mc.rotate(0,60*i,0,p=[0,0,0]) # หมุนไปคนละมุม
mc.parent(['mek%d'%(i+1) for i in range(6)],['mekwiset']) # นำมาผูกรวมกับก้อนกลาง
# สร้างเต่า
mc.polySphere(r=13,sx=6,sy=3,n='kradong')
mc.scale(1,0.5,1)
huahangkha = ['hua','khanasai','khalangsai','hang','khalangkhwa','khanakhwa']
for i in range(6):
mc.polySphere(r=3,n=huahangkha[i])
if(i==0):
mc.scale(1.4,0.8,2.4)
elif(i==3):
mc.scale(1,0.5,3)
else:
mc.scale(1,0.3,2)
mc.move(0,0,10)
mc.rotate(0,60*i,0,p=[0,0,0])
mc.polySphere(r=0.8,n='tasai')
mc.move(1.8,0,16)
mc.polySphere(r=0.8,n='takhwa')
mc.move(-1.8,0,16)
mc.parent('takhwa','tasai','hua')
mc.parent(huahangkha,'kradong')
mc.parent('kradong','mekwiset')
# ตั้งเอ็กซ์เพรชชัน
mc.expression(o='mekwiset',s='tz=30*time') # เมฆเคลื่อนไปข้างหน้า
mc.expression(o='khanasai',s='rx=40*sin(time*%d)'%math.pi) # ขาทั้ง ๔ ขยับไปเรื่อยๆ
mc.expression(o='khalangsai',s='rx=40*cos(time*%d)'%math.pi)
mc.expression(o='khalangkhwa',s='rx=-40*sin(time*%d)'%math.pi)
mc.expression(o='khanakhwa',s='rx=-40*cos(time*%d)'%math.pi)
mc.expression(o='hua',s='tz=5+5*sin(time*%d/5)'%math.pi) # ส่วนหัวก็ขยับ
mc.expression(o='kradong',s='if(time>2.5) ty=16-pow(time-2.5,2)*20; else ty=16') # พอถึงเวลา 2.5 เต่าเริ่มร่วงจากเมฆ

นอกจากนี้ parent() ยังอาจใช้แทน group() โดยแทนที่จะสร้างกลุ่มขึ้นมาเราก็นำวัตถุทั้งหมดไปผูกติดไว้กับอะไรสักอย่าง แทน ซึ่งอาจจะสะดวกกว่าการรวมกลุ่มเฉยๆตรงที่กลุ่มไม่ใช่วัตถุที่มองเห็นได้ เวลาจะเลือกต้องมาเลือกใน outliner ซึ่งบางทีอาจไม่สะดวก
ดังนั้นเราอาจใช้วิธีนำวัตถุมาผูกติดกับวัตถุชนิดหนึ่งที่สามารถมองเห็นได้ในฉาก แต่ไม่มีตัวตนอยู่จริง เป็นเพียงเสมือนเครื่องทำสัญลักษณ์เท่านั้น วัตถุนั้นเรียกว่าโลเคเตอร์ (locator) สามารถสร้างขึ้นมาได้โดยฟังก์ชัน spaceLocator()
การสร้างให้ใส่ตำแหน่งพิกัดที่ต้องการให้ตั้งอยู่ลงในแฟล็ก p (position) และก็สามารถตั้งชื่อด้วยแฟล็ก n (name)
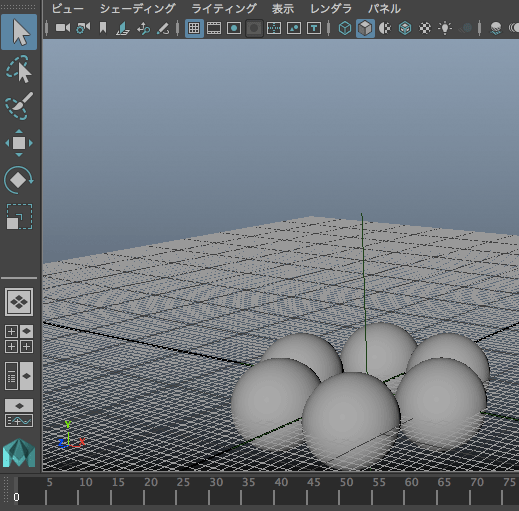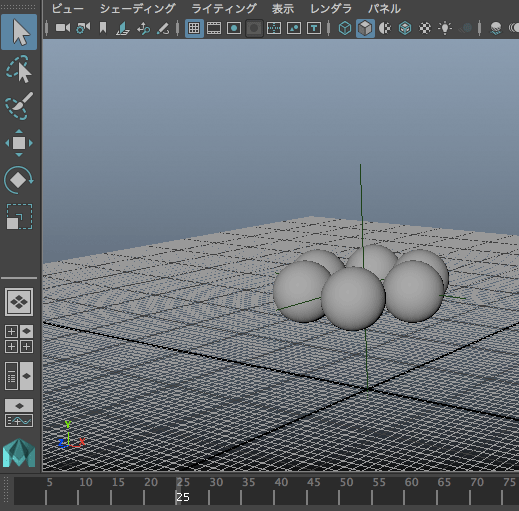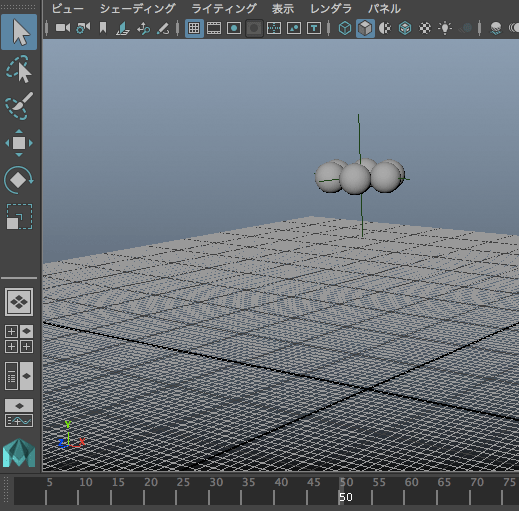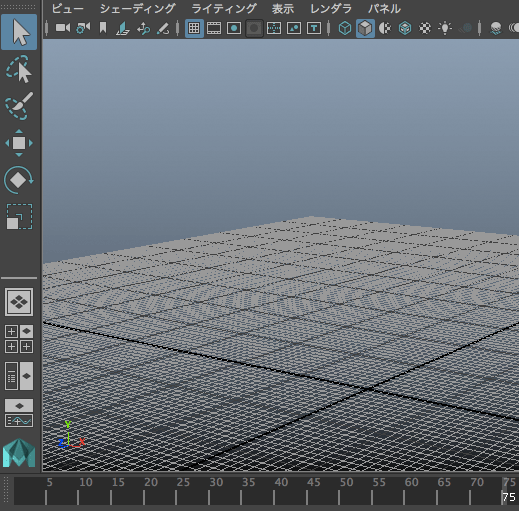
for i in range(6):
mc.polySphere(r=5,sx=18,sy=18,n='luk%d'%(i+1))
mc.move(10,0,0)
mc.rotate(0,60*i,0,p=[0,0,0])
mc.spaceLocator(p=[0,0,0],n='spl')
mc.parent(['luk%d'%(i+1) for i in range(6)]+['spl'])
mc.expression(s='spl.ry=180*time')
mc.expression(o='spl',s='sx=(3.-time)/3; sy=sx; sz=sx')
mc.expression(s='spl.ty=12*time')
mc.setAttr('splShape.lsx',20)
mc.setAttr('splShape.lsy',20)
mc.setAttr('splShape.lsz',20)
mc.polySphere(r=5,sx=18,sy=18,n='luk%d'%(i+1))
mc.move(10,0,0)
mc.rotate(0,60*i,0,p=[0,0,0])
mc.spaceLocator(p=[0,0,0],n='spl')
mc.parent(['luk%d'%(i+1) for i in range(6)]+['spl'])
mc.expression(s='spl.ry=180*time')
mc.expression(o='spl',s='sx=(3.-time)/3; sy=sx; sz=sx')
mc.expression(s='spl.ty=12*time')
mc.setAttr('splShape.lsx',20)
mc.setAttr('splShape.lsy',20)
mc.setAttr('splShape.lsz',20)

๓ บรรทัดสุดท้ายเป็นการปรับขนาดปรากฏของโลเคเตอร์ เพราะขนาดเดิมอาจเล็กไปทำให้สังเกตได้ยาก โดยสามารถไปปรับได้ที่ค่าองค์ประกอบที่อยู่ภายในโหนดที่มีชื่อเป็นชื่อโลเค เตอร์ที่ตั้งบวกด้วย Shape
ค่าขนาดกำหนดโดย lsx (localScaleX) lsy (localScaleY) lsz (localScaleZ)
อีกอย่างที่อาจปรับได้ก็คือตำแหน่ง กำหนดโดย lpx (localPositionX) lpy (localPositionY) lpz (localPositionZ)
ทั้งการปรับขนาดและการเลื่อนแบบนี้จะไม่มีผลต่อวัตถุที่อยู่ภายในเพราะเป็นเพียงองค์ประกอบภายในของตัวโลเคเตอร์เอง
ไม่ว่าโลเคเตอร์จะมีขนาดใหญ่แค่ไหนหรืออยู่ตรงไหนก็ตามเวลาที่เรนเดอร์ภาพออกมาก็จะมองไม่เห็น เพราะเป็นแค่วัตถุสมมุติเท่านั้น
จะใช้ spaceLocator() คู่กับ parent() หรือจะใช้ group() ก็แล้วแต่ความสะดวก
อ้างอิง