maya python เบื้องต้น บทที่ ๑๘: การรวมกลุ่ม
เขียนเมื่อ 2016/03/11 01:09
แก้ไขล่าสุด 2021/09/28 16:42
ในบทที่ผ่านๆมาเราจัดการวัตถุทีละชิ้นแบบไม่ค่อยได้เอามายุ่งเกี่ยวกันสัก เท่าไหร่ แต่ในการใช้งานจริงเรามักจะต้องนำวัตถุหลายๆชิ้นที่สร้างขึ้นมาแล้วนั้นมา ประกอบเข้าด้วยกันเพื่อให้ได้รูปร่างตามที่ต้องการ
การรวมวัตถุหลาย ชิ้นเข้าด้วยกันนั้นอาจทำได้หลายวิธีด้วยกัน วิธีที่ง่ายที่สุดก็คือการนำวัตถุมาจับกลุ่มกันแบบหลวมๆ โดยใช้ฟังก์ชัน group()
วิธีการใช้ฟังก์ชันนี้คือใส่ชื่อของวัตถุที่ต้องการรวมกลุ่มทั้งหมดเข้าไว้ด้วยกัน แล้วตั้งชื่อกลุ่มโดยใช้แฟล็ก n (name)
ขอยกตัวอย่างด้วยการสร้างปูเสฉวนมาสักตัว

สร้างออกมาแล้ว รูปร่างอาจไม่ค่อยเหมือนเท่าไหร่ เอาเป็นว่าไม่ใช่ปูเสฉวนแต่เป็นจานบินรูปปูเสฉวนก็แล้วกัน
ตอนนี้จะเห็นว่าชิ้นส่วนของตัวจานบินมีทั้งหมด ๑๒ ชิ้น แต่ละส่วนนั้นแยกกันต่างหากไม่ขึ้นต่อกัน ในสภาพนี้หากลองลากคลุมเลือกวัตถุทั้งหมดพร้อมกันแล้วใช้ฟังก์ชันrotate() เพื่อหมุน หรือใช้ scale() เพื่อย่อขยายขนาดก็จะพบว่าแต่ละชิ้นแยกกันเปลี่ยนรูป เช่นลอง
จะเห็นว่าผลก็คือเสียรูปไปเลย ไม่ใช่ปูเสฉวนอีกต่อไป

ดังนั้นเพื่อที่จะสามารถทำให้วัตถุทั้งหมดเสมือนเป็นเนื้อเดียวกัน เปลี่ยนแปลงไปด้วยกันตลอด จะต้องทำการรวมกลุ่ม โดยใช้ฟังก์ชัน group()
แบบนี้ทั้งหมดก็จะถูกรวมอยู่ในกล่มที่ชื่อว่า pusechuan ถ้าเปิด outliner ดูก็จะเห็นว่าส่วนประกอบทั้งหมด ๑๒ ส่วนซ่อนอยู่ภายในโหนด pusechuan
หรือถ้าไม่อยากต้องมาใส่ชื่อทั้งหมดลงไปในฟังก์ชัน อาจลองลบทั้งหมดใหม่แล้วพิมพ์สร้างโดยเก็บค่าชื่อของแต่ละส่วนทั้งหมดไว้ใน ตัวแปรหนึ่ง แบบนี้
ในที่นี้ใช้ลิสต์ g เพื่อเก็บรวบรวมชื่อของส่วนประกอบแต่ละส่วนไปเรื่อยๆ โดยใช้แฟล็ก ch เพื่อลบประวัติศาสตร์ไม่ให้คืนค่าโหนดที่เก็บรูปทรงจะได้เหลือแค่โหนดหลัก (รายละเอียดดูบทที่ ๘)
จากนั้นบรรทัดสุดท้ายใช้ group() โดยใส่ลิสต์ g เป็นอาร์กิวเมนต์ เท่ากับเป็นการเอาวัตถุทั้งหมดที่มีชื่อใน g มารวมเป็นกลุ่มเดียวกัน
คราวนี้ลองจับมันมาย่อส่วน เลื่อนตำแหน่ง แล้วก็หมุน
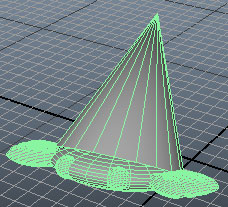
ก็จะพบว่าปูถูกย่อขนาดลงทั้งตัวและเปลี่ยนตำแหน่งและหมุน รูปร่างไม่เปลี่ยนจากเดิม หรือจะจับมันไปหมุนหรือทำอะไรก็ได้ ตราบใดที่เลือกที่ตัวกลุ่ม มันก็จะเกาะกลุ่มกันไปตลอด
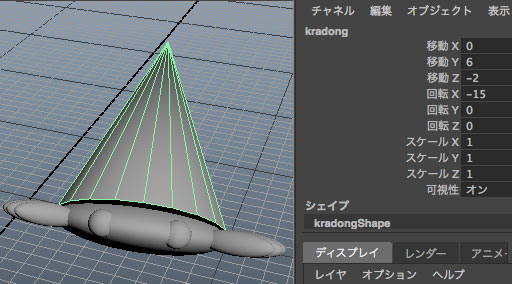
ถ้าลองไปดูที่ค่าองค์ประกอบต่างๆของแต่ละส่วนของปูเสฉวนก็จะเห็นว่ามันไม่ได้ถูกเปลี่ยนไป เลย นั่นเพราะค่าทุกอย่างถูกปรับที่ตัวกลุ่ม ดังนั้นจะเห็นว่าค่าต่างๆของตัววัตถุจะขึ้นกับค่าที่เก็บในโหนดของตัววัตถุ เอง กับที่เก็บในโหนดของกลุ่ม
ตรงจุดนี้มีเรื่องน่าคิดอยู่อย่างว่า ถ้าหากทำการแยกกลุ่มออกไปจะเกิดอะไรขึ้น ว่าแล้วก็ลองทำการแยกกลุ่มดู ทำได้โดยใช้ฟังก์ชัน ungroup()
ลอง
พอทำแบบนี้แล้วไปดูที่แต่ละชิ้นส่วนของตัวปูเสฉวนก็จะเห็นว่าค่าองค์ประกอบ ต่างๆถูกเปลี่ยนแปลงไป โดยที่สัมพันธ์กับค่าที่ถูกปรับที่ตัวกลุ่มไป
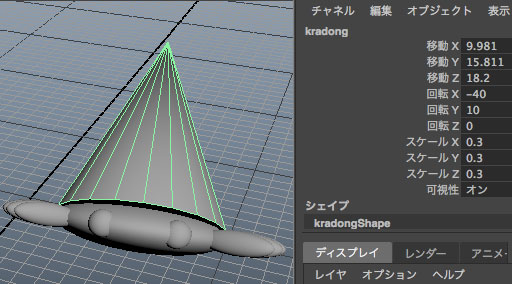
นั่นหมายความว่าพอแยกกลุ่มแล้ว ค่าที่เคยปรับที่ตัวกลุ่มจะถูกแปลงกลายเป็นค่าของตัววัตถุแต่ละตัวโดยตรง
แต่ว่าหากตอนที่ทำการแยกกลุ่มได้เพิ่มแฟล็กลงไปอีกตัวหนึ่งในฟังก์ชันนี้ คือ r (relative)
ลองกดย้อนกลับไปที่ช่วงก่อนทำการแยกกลุ่มแล้วทำการแยกใหม่โดยพิมพ์
แบบนี้จะพบว่าชิ้นส่วนทั้งหมดกลับมาอยู่ในสภาวะก่อนที่จะรวมกลุ่ม ค่าองค์ประกอบต่างๆในแต่ละชิ้นไม่มีการเปลี่ยนแปลง แต่ผลจากการเปลี่ยนแปลงในกลุ่มหายไป ดังนั้นจึงกลับมาอยู่สภาวะเดิม
วัตถุที่ถูกตั้งกลุ่มไว้แล้ว หากมีหลายกลุ่มก็ยังสามารถนำมารวมเป็นกลุ่มที่ใหญ่ขึ้นไปอีกได้ แบบนี้แล้วก็จะเกิดเป็นกลุ่มใหญ่และกลุ่มย่อยซ้อนกัน
เช่น เราอาจสร้างปูเสฉวนแบบนี้ออกมาหลายตัวแล้วเอาหลายตัวนี้มาตั้งเป็นกลุ่มปูเสฉวนขึ้นมา
ขอยกตัวอย่างด้วยการลองสร้างกองทัพยานปูเสฉวนขึ้นมา ในกองหนึ่งมี ๕ ตัว แต่ละตัวประกอบด้วยชิ้นส่วนต่างๆของตัวเอง
ถ้าตั้งชื่อเป็น pusechuan1, pusechuan2 แบบนี้ก็น่าเบื่อแย่ ดังนั้นขอตั้งชื่อให้แต่ละตัวโดยใช้ชื่อของหน่วยรบพิเศษกีนิว ตัวละครจากการ์ตูนเรื่องดรากอนบอล
หน่วยรบพิเศษกีนิวมีสมาชิก ๕ คน แต่ละคนมีขนาดร่างกายใหญ่ไม่เท่ากัน สมาชิกทั้งหมดมีชื่อดังนี้
['ginyuu','rikuumu','baata','jiisu','gurudo']
ลองสร้างกองทัพยานปูขึ้นมาโดยใช้แต่ละตัวมีขนาดไม่เท่ากัน ตั้งอยู่ในตำแหน่งต่างกัน นอกจากนี้ทำให้มีการเคลื่อนไหวด้วย โดยแต่ละตัวมีการเคลื่อนที่ไปข้างหน้าพร้อมกัน พร้อมกันนั้นก็เคลื่อนที่ขึ้นลงไปด้วยโดยมีความเร็วต่างๆกัน ตัวเล็กเคลื่อนที่ไวกว่า
สร้างลิสต์ของลิสต์ที่บรรจุตัวแปร ๕ ตัว [ชื่อ, ขนาด, ตำแหน่งในแกน x, ตำแหน่งในแกน z, ความเร็วในการเคลื่อนที่]
ผลที่ได้ดูในคลิป
จะเห็นว่ามีการใช้เอ็กซ์เพรชชันอยู่ ๒ ส่วน คือใช้แยกภายในตัวยานปูแต่ละตัวเพื่อให้เกิดการเคลื่อนที่ขึ้นลง และอีกส่วนคือใช้กับตัวกลุ่มโดยให้เคลื่อนที่ไปข้างหน้าด้วยความเร็วคงที่
ผลที่ได้ก็คือกองทัพยานปูเสฉวนที่เคลื่อนไปข้างหน้าร่วมกันทั้งกลุ่มพร้อมทั้ง มีการขยับขึ้นลงซึ่งเป็นการเคลื่อนที่ย่อยของสมาชิกแต่ละตัว
จากตัวอย่างจะเห็นประโยชน์ของการรวมกลุ่ม สามารถนำไปประยุกต์อะไรต่างๆใช้ประโยชน์ได้มากมาย
อ้างอิง
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/group.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/ungroup.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/pickWalk.html
https://ja.wikipedia.org/wiki/ギニュー特戦隊
การรวมวัตถุหลาย ชิ้นเข้าด้วยกันนั้นอาจทำได้หลายวิธีด้วยกัน วิธีที่ง่ายที่สุดก็คือการนำวัตถุมาจับกลุ่มกันแบบหลวมๆ โดยใช้ฟังก์ชัน group()
วิธีการใช้ฟังก์ชันนี้คือใส่ชื่อของวัตถุที่ต้องการรวมกลุ่มทั้งหมดเข้าไว้ด้วยกัน แล้วตั้งชื่อกลุ่มโดยใช้แฟล็ก n (name)
ขอยกตัวอย่างด้วยการสร้างปูเสฉวนมาสักตัว
mc.polyCone(r=5,h=12,n='kradong') # ส่วนกระดอง
mc.rotate(-15,0,0)
mc.move(0,6,-2)
mc.polySphere(r=5,n='lamtua') # ส่วนลำตัว
mc.scale(1,0.3,1)
mc.polySphere(r=0.8,n='tasai') # ส่วนตาซ้าย
mc.move(2,0,4)
mc.polySphere(r=0.8,n='takhwa') # ส่วนตาขวา
mc.move(-2,0,4)
for r in [0,10,20,30,150,160,170,180]:
mc.polySphere(r=0.7,n='kha1') # ส่วนขาทั้งหมด ๘ ข้าง
mc.scale(3,1,1)
mc.move(6,0,0)
mc.rotate(0,-r,0,p=[0,0,0])
mc.rotate(-15,0,0)
mc.move(0,6,-2)
mc.polySphere(r=5,n='lamtua') # ส่วนลำตัว
mc.scale(1,0.3,1)
mc.polySphere(r=0.8,n='tasai') # ส่วนตาซ้าย
mc.move(2,0,4)
mc.polySphere(r=0.8,n='takhwa') # ส่วนตาขวา
mc.move(-2,0,4)
for r in [0,10,20,30,150,160,170,180]:
mc.polySphere(r=0.7,n='kha1') # ส่วนขาทั้งหมด ๘ ข้าง
mc.scale(3,1,1)
mc.move(6,0,0)
mc.rotate(0,-r,0,p=[0,0,0])

สร้างออกมาแล้ว รูปร่างอาจไม่ค่อยเหมือนเท่าไหร่ เอาเป็นว่าไม่ใช่ปูเสฉวนแต่เป็นจานบินรูปปูเสฉวนก็แล้วกัน
ตอนนี้จะเห็นว่าชิ้นส่วนของตัวจานบินมีทั้งหมด ๑๒ ชิ้น แต่ละส่วนนั้นแยกกันต่างหากไม่ขึ้นต่อกัน ในสภาพนี้หากลองลากคลุมเลือกวัตถุทั้งหมดพร้อมกันแล้วใช้ฟังก์ชันrotate() เพื่อหมุน หรือใช้ scale() เพื่อย่อขยายขนาดก็จะพบว่าแต่ละชิ้นแยกกันเปลี่ยนรูป เช่นลอง
mc.scale(0.3,0.3,0.3,'kradong','lamtua','tasai','takhwa',['kha%d'%i for i in range(1,9)],r=1)
จะเห็นว่าผลก็คือเสียรูปไปเลย ไม่ใช่ปูเสฉวนอีกต่อไป

ดังนั้นเพื่อที่จะสามารถทำให้วัตถุทั้งหมดเสมือนเป็นเนื้อเดียวกัน เปลี่ยนแปลงไปด้วยกันตลอด จะต้องทำการรวมกลุ่ม โดยใช้ฟังก์ชัน group()
mc.group('kradong','lamtua','tasai','takhwa',['kha%d'%i for i in range(1,9)],n='pusechuan')
แบบนี้ทั้งหมดก็จะถูกรวมอยู่ในกล่มที่ชื่อว่า pusechuan ถ้าเปิด outliner ดูก็จะเห็นว่าส่วนประกอบทั้งหมด ๑๒ ส่วนซ่อนอยู่ภายในโหนด pusechuan
หรือถ้าไม่อยากต้องมาใส่ชื่อทั้งหมดลงไปในฟังก์ชัน อาจลองลบทั้งหมดใหม่แล้วพิมพ์สร้างโดยเก็บค่าชื่อของแต่ละส่วนทั้งหมดไว้ใน ตัวแปรหนึ่ง แบบนี้
g = [] # สร้างลิสต์เก็บชื่อชิ้นส่วน
g += mc.polyCone(r=5,h=12,ch=0,n='kradong') # สร้างกระดองพร้อมเก็บชื่อเข้าลิสต์
mc.rotate(-15,0,0)
mc.move(0,6,-2)
g += mc.polySphere(r=5,ch=0,n='lamtua')
mc.scale(1,0.3,1)
g += mc.polySphere(r=0.8,ch=0,n='tasai')
mc.move(2,0,4)
g += mc.polySphere(r=0.8,ch=0,n='takhwa')
mc.move(-2,0,4)
for r in [0,10,20,30,150,160,170,180]:
g += mc.polySphere(r=0.7,ch=0,n='kha1')
mc.scale(3,1,1)
mc.move(6,0,0)
mc.rotate(0,-r,0,p=[0,0,0])
mc.group(g,n='pusechuan')
g += mc.polyCone(r=5,h=12,ch=0,n='kradong') # สร้างกระดองพร้อมเก็บชื่อเข้าลิสต์
mc.rotate(-15,0,0)
mc.move(0,6,-2)
g += mc.polySphere(r=5,ch=0,n='lamtua')
mc.scale(1,0.3,1)
g += mc.polySphere(r=0.8,ch=0,n='tasai')
mc.move(2,0,4)
g += mc.polySphere(r=0.8,ch=0,n='takhwa')
mc.move(-2,0,4)
for r in [0,10,20,30,150,160,170,180]:
g += mc.polySphere(r=0.7,ch=0,n='kha1')
mc.scale(3,1,1)
mc.move(6,0,0)
mc.rotate(0,-r,0,p=[0,0,0])
mc.group(g,n='pusechuan')
ในที่นี้ใช้ลิสต์ g เพื่อเก็บรวบรวมชื่อของส่วนประกอบแต่ละส่วนไปเรื่อยๆ โดยใช้แฟล็ก ch เพื่อลบประวัติศาสตร์ไม่ให้คืนค่าโหนดที่เก็บรูปทรงจะได้เหลือแค่โหนดหลัก (รายละเอียดดูบทที่ ๘)
จากนั้นบรรทัดสุดท้ายใช้ group() โดยใส่ลิสต์ g เป็นอาร์กิวเมนต์ เท่ากับเป็นการเอาวัตถุทั้งหมดที่มีชื่อใน g มารวมเป็นกลุ่มเดียวกัน
คราวนี้ลองจับมันมาย่อส่วน เลื่อนตำแหน่ง แล้วก็หมุน
mc.scale(0.3,0.3,0.3,'pusechuan')
mc.move(10,10,20,'pusechuan')
mc.rotate(-25,10,0,'pusechuan')
mc.move(10,10,20,'pusechuan')
mc.rotate(-25,10,0,'pusechuan')

ก็จะพบว่าปูถูกย่อขนาดลงทั้งตัวและเปลี่ยนตำแหน่งและหมุน รูปร่างไม่เปลี่ยนจากเดิม หรือจะจับมันไปหมุนหรือทำอะไรก็ได้ ตราบใดที่เลือกที่ตัวกลุ่ม มันก็จะเกาะกลุ่มกันไปตลอด
ถ้าลองไปดูที่ค่าองค์ประกอบต่างๆของแต่ละส่วนของปูเสฉวนก็จะเห็นว่ามันไม่ได้ถูกเปลี่ยนไป เลย นั่นเพราะค่าทุกอย่างถูกปรับที่ตัวกลุ่ม ดังนั้นจะเห็นว่าค่าต่างๆของตัววัตถุจะขึ้นกับค่าที่เก็บในโหนดของตัววัตถุ เอง กับที่เก็บในโหนดของกลุ่ม

ตรงจุดนี้มีเรื่องน่าคิดอยู่อย่างว่า ถ้าหากทำการแยกกลุ่มออกไปจะเกิดอะไรขึ้น ว่าแล้วก็ลองทำการแยกกลุ่มดู ทำได้โดยใช้ฟังก์ชัน ungroup()
ลอง
mc.ungroup('pusechuan')
พอทำแบบนี้แล้วไปดูที่แต่ละชิ้นส่วนของตัวปูเสฉวนก็จะเห็นว่าค่าองค์ประกอบ ต่างๆถูกเปลี่ยนแปลงไป โดยที่สัมพันธ์กับค่าที่ถูกปรับที่ตัวกลุ่มไป

นั่นหมายความว่าพอแยกกลุ่มแล้ว ค่าที่เคยปรับที่ตัวกลุ่มจะถูกแปลงกลายเป็นค่าของตัววัตถุแต่ละตัวโดยตรง
แต่ว่าหากตอนที่ทำการแยกกลุ่มได้เพิ่มแฟล็กลงไปอีกตัวหนึ่งในฟังก์ชันนี้ คือ r (relative)
ลองกดย้อนกลับไปที่ช่วงก่อนทำการแยกกลุ่มแล้วทำการแยกใหม่โดยพิมพ์
mc.ungroup('pusechuan',r=1)
แบบนี้จะพบว่าชิ้นส่วนทั้งหมดกลับมาอยู่ในสภาวะก่อนที่จะรวมกลุ่ม ค่าองค์ประกอบต่างๆในแต่ละชิ้นไม่มีการเปลี่ยนแปลง แต่ผลจากการเปลี่ยนแปลงในกลุ่มหายไป ดังนั้นจึงกลับมาอยู่สภาวะเดิม
วัตถุที่ถูกตั้งกลุ่มไว้แล้ว หากมีหลายกลุ่มก็ยังสามารถนำมารวมเป็นกลุ่มที่ใหญ่ขึ้นไปอีกได้ แบบนี้แล้วก็จะเกิดเป็นกลุ่มใหญ่และกลุ่มย่อยซ้อนกัน
เช่น เราอาจสร้างปูเสฉวนแบบนี้ออกมาหลายตัวแล้วเอาหลายตัวนี้มาตั้งเป็นกลุ่มปูเสฉวนขึ้นมา
ขอยกตัวอย่างด้วยการลองสร้างกองทัพยานปูเสฉวนขึ้นมา ในกองหนึ่งมี ๕ ตัว แต่ละตัวประกอบด้วยชิ้นส่วนต่างๆของตัวเอง
ถ้าตั้งชื่อเป็น pusechuan1, pusechuan2 แบบนี้ก็น่าเบื่อแย่ ดังนั้นขอตั้งชื่อให้แต่ละตัวโดยใช้ชื่อของหน่วยรบพิเศษกีนิว ตัวละครจากการ์ตูนเรื่องดรากอนบอล
หน่วยรบพิเศษกีนิวมีสมาชิก ๕ คน แต่ละคนมีขนาดร่างกายใหญ่ไม่เท่ากัน สมาชิกทั้งหมดมีชื่อดังนี้
['ginyuu','rikuumu','baata','jiisu','gurudo']
ลองสร้างกองทัพยานปูขึ้นมาโดยใช้แต่ละตัวมีขนาดไม่เท่ากัน ตั้งอยู่ในตำแหน่งต่างกัน นอกจากนี้ทำให้มีการเคลื่อนไหวด้วย โดยแต่ละตัวมีการเคลื่อนที่ไปข้างหน้าพร้อมกัน พร้อมกันนั้นก็เคลื่อนที่ขึ้นลงไปด้วยโดยมีความเร็วต่างๆกัน ตัวเล็กเคลื่อนที่ไวกว่า
สร้างลิสต์ของลิสต์ที่บรรจุตัวแปร ๕ ตัว [ชื่อ, ขนาด, ตำแหน่งในแกน x, ตำแหน่งในแกน z, ความเร็วในการเคลื่อนที่]
import math
# กำหนดค่าต่างๆของแต่ละตัว
ginyuu = [['ginyuu',1,0,0,1.5],['rikuumu',1.25,18,-8,2],['baata',1.5,-18,-8,2.5],['jiisu',0.75,-10,14,1],['gurudo',0.5,10,14,0.5]]
# เริ่มวนซ้ำเพื่อสร้างปูแต่ละตัว
for pu in ginyuu:
g = [] # เตรียมลิสต์สำหรับเก็บชื่อชิ้นส่วนตัวปู
g += mc.polyCone(r=5,h=12,ch=0,n='kradong')
mc.rotate(-15,0,0)
mc.move(0,6,-2)
g += mc.polySphere(r=5,ch=0,n='lamtua')
mc.scale(1,0.3,1)
g += mc.polySphere(r=0.8,ch=0,n='tasai')
mc.move(2,0,4)
g += mc.polySphere(r=0.8,ch=0,n='takhwa')
mc.move(-2,0,4)
for r in [0,10,20,30,150,160,170,180]:
g += mc.polySphere(r=0.7,ch=0,n='kha1')
mc.scale(3,1,1)
mc.move(6,0,0)
mc.rotate(0,-r,0,p=[0,0,0])
mc.group(g,n=pu[0]) # นำชิ้นส่วนทั้งหมดมารวมกลุ่ม
mc.scale(pu[1],pu[1],pu[1],p=[0,0,0]) # ขยายหรือย่อขนาดตามมาตราส่วนของแต่ละตัว
mc.move(pu[2],0,pu[3]) # ย้ายไปประจำตำแหน่งที่ต่างกัน
mc.expression(o=pu[0],s='ty=10*sin(time*2*%f/%f)'%(math.pi,pu[4])) # สร้างเอ็กซ์เพรชชันการเคลื่อนที่แต่ละตัว
mc.group([r[0] for r in ginyuu],n='nuairopphiset_ginyuu') # เอาทุกตัวมารวมกลุ่มกัน
mc.expression(o='nuairopphiset_ginyuu',s='tz=time*8') # สร้างเอ็กซืเพรชชันการเคลื่อนที่ไปข้างหน้าของทุกตัว
# กำหนดค่าต่างๆของแต่ละตัว
ginyuu = [['ginyuu',1,0,0,1.5],['rikuumu',1.25,18,-8,2],['baata',1.5,-18,-8,2.5],['jiisu',0.75,-10,14,1],['gurudo',0.5,10,14,0.5]]
# เริ่มวนซ้ำเพื่อสร้างปูแต่ละตัว
for pu in ginyuu:
g = [] # เตรียมลิสต์สำหรับเก็บชื่อชิ้นส่วนตัวปู
g += mc.polyCone(r=5,h=12,ch=0,n='kradong')
mc.rotate(-15,0,0)
mc.move(0,6,-2)
g += mc.polySphere(r=5,ch=0,n='lamtua')
mc.scale(1,0.3,1)
g += mc.polySphere(r=0.8,ch=0,n='tasai')
mc.move(2,0,4)
g += mc.polySphere(r=0.8,ch=0,n='takhwa')
mc.move(-2,0,4)
for r in [0,10,20,30,150,160,170,180]:
g += mc.polySphere(r=0.7,ch=0,n='kha1')
mc.scale(3,1,1)
mc.move(6,0,0)
mc.rotate(0,-r,0,p=[0,0,0])
mc.group(g,n=pu[0]) # นำชิ้นส่วนทั้งหมดมารวมกลุ่ม
mc.scale(pu[1],pu[1],pu[1],p=[0,0,0]) # ขยายหรือย่อขนาดตามมาตราส่วนของแต่ละตัว
mc.move(pu[2],0,pu[3]) # ย้ายไปประจำตำแหน่งที่ต่างกัน
mc.expression(o=pu[0],s='ty=10*sin(time*2*%f/%f)'%(math.pi,pu[4])) # สร้างเอ็กซ์เพรชชันการเคลื่อนที่แต่ละตัว
mc.group([r[0] for r in ginyuu],n='nuairopphiset_ginyuu') # เอาทุกตัวมารวมกลุ่มกัน
mc.expression(o='nuairopphiset_ginyuu',s='tz=time*8') # สร้างเอ็กซืเพรชชันการเคลื่อนที่ไปข้างหน้าของทุกตัว
ผลที่ได้ดูในคลิป
จะเห็นว่ามีการใช้เอ็กซ์เพรชชันอยู่ ๒ ส่วน คือใช้แยกภายในตัวยานปูแต่ละตัวเพื่อให้เกิดการเคลื่อนที่ขึ้นลง และอีกส่วนคือใช้กับตัวกลุ่มโดยให้เคลื่อนที่ไปข้างหน้าด้วยความเร็วคงที่
ผลที่ได้ก็คือกองทัพยานปูเสฉวนที่เคลื่อนไปข้างหน้าร่วมกันทั้งกลุ่มพร้อมทั้ง มีการขยับขึ้นลงซึ่งเป็นการเคลื่อนที่ย่อยของสมาชิกแต่ละตัว
จากตัวอย่างจะเห็นประโยชน์ของการรวมกลุ่ม สามารถนำไปประยุกต์อะไรต่างๆใช้ประโยชน์ได้มากมาย
อ้างอิง
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/group.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/ungroup.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/pickWalk.html
https://ja.wikipedia.org/wiki/ギニュー特戦隊