ต่อจาก บทที่ ๑๙

ในบทนี้จะเข้าสู่เรื่องของโครงข่ายประสาทแบบคอนโวลูชัน (卷积神经网路, convolutional neural network) หรือนิยมเรียกย่อว่า CNN

โครงข่ายปราสาทเทียมชนิดนี้นิยมใช้ในการวิเคราะห์ภาพหรืออนุกรมเวลาซึ่งเป็นข้อมูลที่มีความต่อเนื่อง มีการใช้งานที่กว้างขวางมากมาย




ว่าด้วยเรื่องของข้อมูลที่มีความเกี่ยวพันเชิงตำแหน่งหรือลำดับ

ข้อมูลบางประเภทเป็นตัวแปรที่มีความต่อเนื่องเกี่ยวพันกันเชิงตำแหน่งหรือลำดับหรือเวลา เช่น รายได้ในแต่ละเดือน ซึ่งอาจวาดเป็นกราฟได้แบบนี้



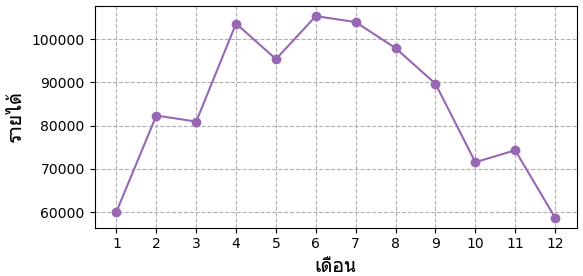
ในข้อมูลนี้เมื่อทำการวิเคราะห์เราคงไม่ได้สนแค่ว่าแต่ละเดือนมีค่าเท่าไหร่บ้าง แต่สนใจความสัมพันธ์ของเดือนที่อยู่ติดกันด้วย เช่นเดือน 2 เพิ่มจากเดือน 1 แต่เดือน 3 ลดลงเล็กน้อย เป็นต้น

ข้อมูลที่แสดงลำดับการเปลี่ยนแปลงของค่าตามเวลาแบบนี้เรียกว่าอนุกรมเวลา (时间序列, time series)

  ข้อมูลลักษณะแบบนี้ ความสัมพันธ์ระหว่างค่าของจุดข้างเคียงกันมีความสำคัญ และลำดับข้อมูลก็มีความสำคัญ

แต่ในโครงข่ายประสาทแบบเพอร์เซปตรอนหลายชั้นแบบเดิมนั้นข้อมูลทั้งหมดจะถูกป้อนเข้ามาในฐานะข้อมูลตัวแปรหนึ่งเหมือนๆกันหมด

นั่นคือ แต่ละจุดบนเส้นกราฟ จะถูกนำมาแยกใส่ในแต่ละช่องข้อมูล ไม่ได้ถูกใส่ในฐานะเส้นต่อเนื่อง อาจมองภาพได้เป็นแบบนี้



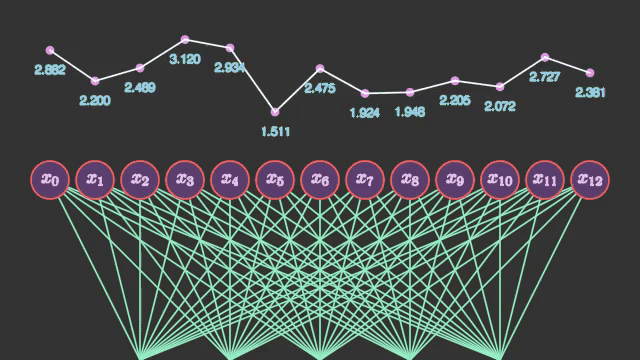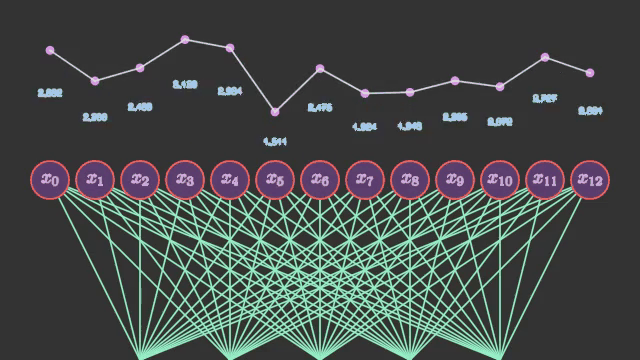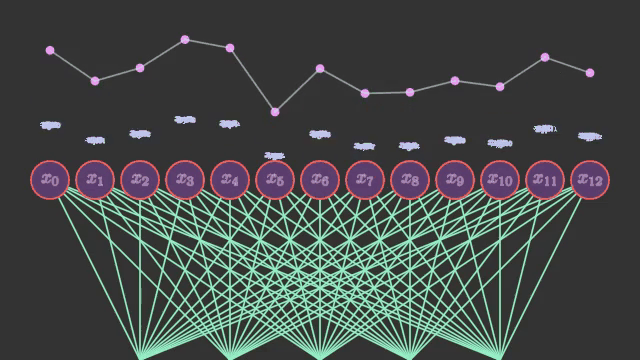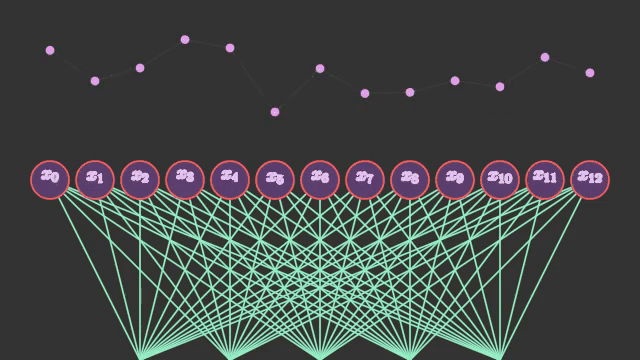
ค่าในแต่ละเซลล์ของโครงข่ายประสาทนั้นแม้จะเห็นว่าเรียงลำดับกันอยู่ก็จริง แต่ลำดับนั้นไม่ได้มีความหมายอะไร ไม่ใช่ว่าเซลล์ที่อยู่ติดกันจะมีความใกล้ชิดกับเซลล์ข้างๆ ต่อให้สลับลำดับกันไปก็ไม่มีอะไรเปลี่ยนแปลง

แต่ในโครงข่ายประสาทแบบคอนโวลูชันที่จะกล่าวถึงต่อไปนี้จะพิจารณาความสัมพันธ์ระหว่างจุดข้างเคียง อาจมองภาพได้เป็นแบบนี้



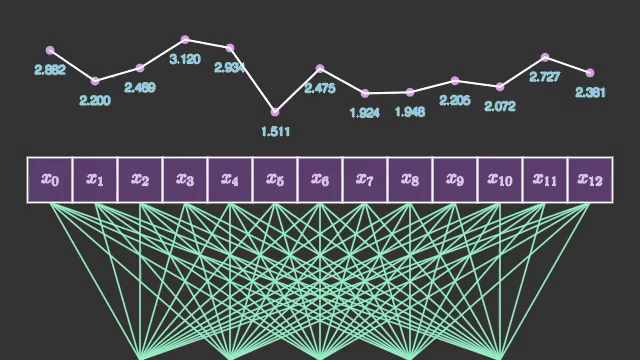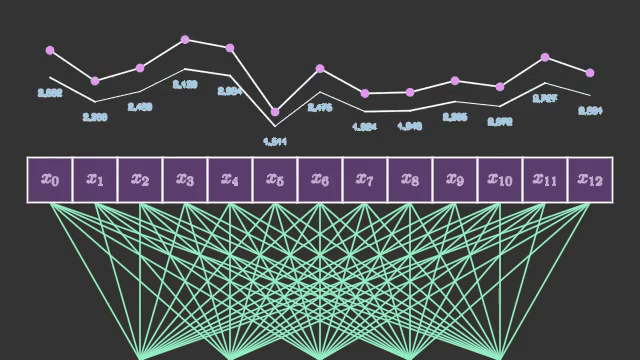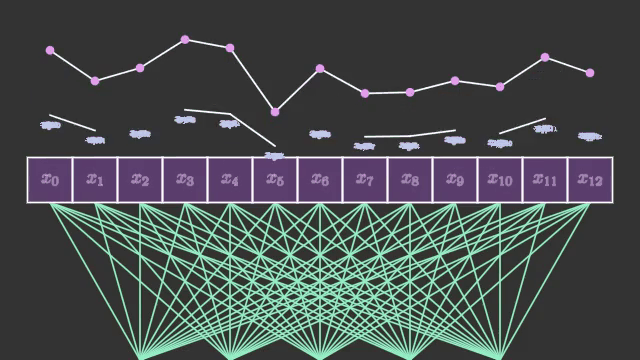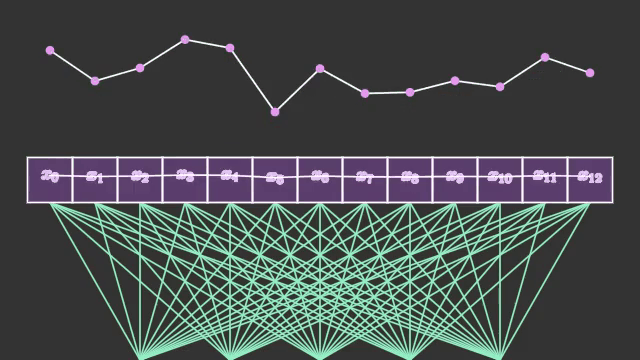
การคำนวณที่เกิดขึ้นภายในชั้นคอนโวลูชันแต่ละชั้นนั้นถือเป็นเรื่องที่เข้าใจยากมากพอสมควร เนื่องจากข้อมูลที่เข้าสู่การคำนวณนั้นเป็นอาเรย์หลายมิติ

โครงข่ายประสาทแบบคอนโวลูชันมีทั้งแบบหนึ่งมิติและสองมิติ หรือจำนวนมิติมากกว่านั้น ความซับซ้อนจะมากขึ้นตามลำดับ

คนส่วนใหญ่คงจะคุ้นเคยกับแบบสองมิติ เพราะเป็นที่ใช้แพร่หลายในการวิเคราะห์รูปภาพ ซึ่งรูปภาพเป็นข้อมูลสองมิติ

แต่ในที่นี้จะขอไปทีละขั้น โดยบทนี้จะเริ่มจากอธิบายแบบหนึ่งมิติก่อน โดยตัวอย่างที่พบได้ทั่วไปคือข้อมูลอนุกรมเวลา

ตัวอย่างหนึ่งสำหรับงานวิจัยที่ใช้คอนโวลูชันหนึ่งมิติวิเคราะห์คือการวิเคราะห์กราฟแสงของดาวเพื่อค้นหาดาวเคราะห์ อ่านรายละเอียดได้ใน https://phyblas.hinaboshi.com/20171216




โครงสร้างของโครงข่ายประสาทแบบคอนโวลูชัน

โดยทั่วไปแล้วโครงข่ายประสาทแบบคอนโวลูชันจะประกอบไปด้วย ๒ ส่วนคือ

- ส่วนคอนโวลูชัน ประกอบไปด้วย
-- ชั้นคอนโวลูชัน (convolutional layer)
-- ฟังก์ชันกระตุ้น อย่างเช่น ReLU
-- ชันบ่อรวมสูงสุด (max pooling layer)

- ส่วนเชิงเส้น ประกอบไปด้วย
-- ชั้นเชิงเส้น (affine layer)
-- ฟังก์ชันกระตุ้น อย่างเช่น ReLU ยกเว้นชั้นสุดท้ายใช้ Softmax หรือ Sigmoid


ตัวอย่างเช่นโครงสร้างแบบในภาพนี้



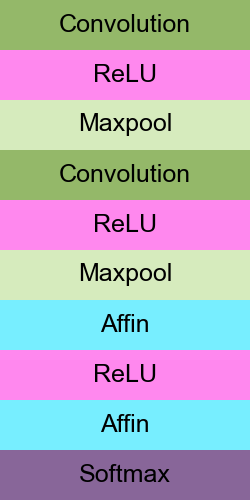
ชั้นคอนโวลูชัน (convolutional layer) กับชันบ่อรวมสูงสุด (max pooling layer) นั้นกำลังจะกล่าวถึงต่อไปในบทนี้ ส่วนชั้นที่เหลือมีเขียนอธิบายในบทก่อนหน้าไปแล้ว โค้ดจะใช้ตามในบทที่ ๑๑

ในโครงสร้างนี้ข้อมูลจะเริ่มเข้ามาในโครงข่ายประสาทโดยเริ่มผ่านจากส่วนคอนโวลูชัน ซึ่งอาจมีกี่ชั้นก็ได้ ในแต่ละชั้นจะประกอบไปด้วยชั้นย่อยที่ประกอบไปด้วยชั้นคอนโวลูชัน ตามด้วยฟังก์ชันกระตุ้นและชั้นบ่อรวมสูงสุด ทั้งหมดนี้นับรวมเป็น ๑ ชั้น

หลังจากผ่านส่วนคอนโวลูชันแล้วก็ยังจะต้องเข้าสู่ส่วนคำนวณเชิงเส้น ซึ่งส่วนนี้จะมีการคำนวณที่เหมือนกับเพอร์เซปตรอนหลายชั้นแบบธรรมดา คือประกอบไปด้วยชั้นเชิงเส้นตามด้วยฟังก์ชันกระตุ้น

ตัวอย่างในภาพนี้มีชั้นคอนโวลูชัน ๒ ชั้น ชั้นเชิงเส้น ๒ ชั้น รวมเป็น ๔ ชั้น

หากเขียนการคำนวณภายในแต่ละชั้นไปทีละขั้นก็อาจเขียนได้แบบนี้

ชั้น 1

$\begin{align} a_1 &= \textbf{Convolution}(x) \\ A_1 &= \textbf{ReLU}(a_1) \\ h_1 &= \textbf{Maxpool}(A_1) \end{align}$ ..(20.1)

ชั้น 2

$\begin{align} a_2 &= \textbf{Convolution}(h_1) \\ A_2 &= \textbf{ReLU}(a_2) \\ h_2 &= \textbf{Maxpool}(A_2) \end{align}$ ..(20.2)

ชั้น 3

$\begin{align} a_3 &= \textbf{Affin}(h_2) \\ h_3 &= \textbf{ReLU}(a_3) \end{align}$ ..(20.3)

ชั้น 4

$\begin{align} a_4 &= \textbf{Affin}(h_3) \\ h_4 &= \textbf{Softmax}(a_4) \end{align}$ ..(20.4)

โดยในที่นี้ $x,h_1,h_2,h_3$ คืออาเรย์ข้อมูลขาเข้าของชั้นที่ 1,2,3,4 ตามลำดับ

และ $h_1,h_2,h_3,h_4$ คืออาเรย์ข้อมูลขาออกชั้นที่ 1,2,3,4 ตามลำดับ

สรุปโดยรวมแล้ว โครงข่ายประสาทแบบคอนโวลูชันคือเพอร์เซปตรอนหลายชั้นที่เพิ่มส่วนคอนโวลูชันเข้ามาในช่วงต้นของโครงข่าย การคำนวณในชั้นคอนโวลูชันเป็นส่วนสำคัญที่สุดของโครงข่ายประสาทแบบคอนโวลูชัน แต่พอผ่านชั้นคอนโวลูชันเสร็จก็ยังจะต้องผ่านชั้นคำนวณเชิงเส้นเหมือนเพอร์เซปตรอนหลายชั้นธรรมดา




สหสัมพันธ์ไขว้และคอนโวลูชัน

เพื่อที่จะวิเคราะห์ความสัมพันธ์ระหว่างจุดต่างๆที่อยู่ติดกัน การคำนวณที่เกิดขึ้นภายในชั้นคอนโวลูชันนั้นมีพื้นฐานมาจากการคำนวณสหสัมพันธ์ไขว้ (cross-correlation) ซึ่งมักถูกเรียกเป็นคอนโวลูชัน จึงเป็นที่มาที่ทำให้เรียกว่าโครงข่ายประสาทแบบคอนโวลูชัน

รายละเอียดเกี่ยวกับเรื่องสหสัมพันธ์ไขว้และคอนโวลูชันนี้ค่อนข้างยาว และไม่ได้ใช้แค่ในเรื่องของโครงข่ายประสาทเทียม ดังนั้นจึงขอเขียนแยกไว้ โดยได้อธิบายไว้ในบทความนี้ ขอให้ข้ามไปอ่านแล้วค่อยกลับมาอ่านหน้านี้ต่อ https://phyblas.hinaboshi.com/20180609

สรุปคร่าวๆตรงนี้อีกครั้งก็คือ การคำนวณสหสัมพันธ์ไขว้คือการที่เรามีตัวกรองเป็นค่าตัวเลขชุดหนึ่ง แล้วเอามันมาวิ่งไล่จับคู่คูณกับแผงค่าตัวแปรตั้งต้น ผลที่ได้จะออกมาเป็นผลรวมของผลคูณทุกคู่

สำหรับกรณีหนึ่งมิติ มองภาพตัวอย่างเป็นภาพเคลื่อนไหวเพื่อให้เข้าใจได้ง่ายขึ้น



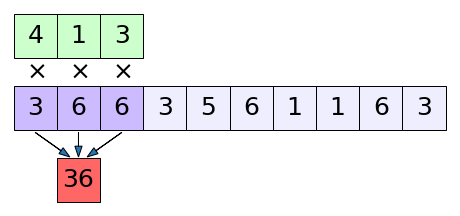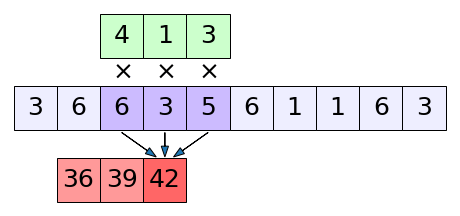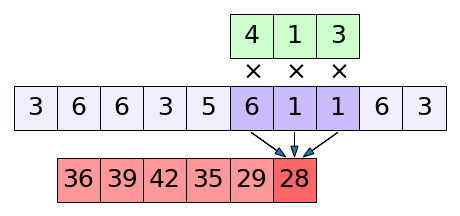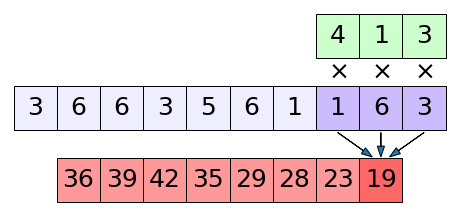
จะเห็นว่าในการคำนวณแบบนี้มีการเอาจุดที่อยู่ใกล้ๆกันมาคิดคำนวณร่วมกัน ดังนั้นความสัมพันธ์ของจุดข้างเคียงจึงถูกพิจารณา

ด้วยเหตุนี้การคำนวณสหสัมพันธ์ไขว้จึงถูกนำมาใช้เพื่อวิเคราะห์ข้อมูลที่ต้องการพิจารณาความสัมพันธ์ระหว่างจุดที่อยู่ใกล้กัน

แต่การคำนวณที่เกิดขึ้นในชั้นคอนโวลูชันจริงๆนั้นไม่ใช่เกิดจากตัวกรองเพียงตัวเดียวดังเช่นในภาพนี้ แต่จะใช้หลายตัวกรองวิ่งไปพร้อมกันเพื่อคำนวณผลแยกกัน หากวาดภาพแล้วจะซับซ้อนขึ้นไปกว่านี้ ซึ่งจะกล่าวถึงต่อไป




การคำนวณภายในชั้นคอนโวลูชัน

คราวนี้มาดูการคำนวณที่เกิดขึ้นโดยทั่วไปในชั้นคอนโวลูชัน

จากสมการ (20.1) และ (20.2) ซึ่งมีชั้นคอนโวลูชัน จะเกิดการคำนวณแบบนี้ขึ้นภายในชั้นนี้

$\begin{align} a_1^{(ι,j,t)} &= \sum_{i=1}^{c_0}\sum_{μ=1}^{k_1} w_1^{(i,j,μ)}x^{(ι,i,t-1+μ)} + b_1^{(j)} \end{align}$ ..(20.5)

$\begin{align} a_2^{(ι,j,t)} &= \sum_{i=1}^{c_1}\sum_{μ=1}^{k_2} w_2^{(i,j,μ)}h_1^{(ι,i,t-1+μ)} + b_2^{(j)} \end{align}$ ..(20.6)

ในที่นี้ $c_0$ คือจำนวนช่องของข้อมูลขาเข้าของชั้นที่ 1

$c_1$ คือจำนวนช่องของข้อมูลขาออกของชั้นที่ 1 และเท่ากับจำนวนช่องของข้อมูลขาเข้าในชั้นที่ 2

$k_1$ และ $k_2$ คือความยาวของตัวกรองในชั้นที่ 1 และ 2 ตามลำดับ

ตัว $ι,i,j,t,μ$ ที่ใส่อยู่ในวงเล็บลอยอยู่ด้านบนคือดัชนีชี้ว่าเป็นค่าตัวไหน

$ι$ คือดัชนีบอกว่าเป็นข้อมูลตัวที่เท่าไหร่

$i$ คือดัชนีบอกลำดับช่องของข้อมูลขาเข้าของชั้นนั้น

$j$ คือดัชนีลอบลำดับช่องของข้อมูลขาออกของชั้นนั้น

$t$ คือดัชนีบอกลำดับข้อมูลในอนุกรมเวลา

และ $μ$ เป็นดัชนีบอกตำแหน่งภายในตัวกรอง

พารามิเตอร์ของชั้นคอนโวลูชันคือ w ค่าน้ำหนักภายในแต่ละช่องในชั้นนั้นคือ กับ b ไบแอสของแต่ละชั้น

จำนวนพารามิเตอร์ w จะเป็นผลคูณของ: จำนวนช่องของข้อมูลขาเข้า × จำนวนช่องของข้อมูลขาออก × ความยาวตัวกรอง

เช่น สำหรับชั้นแรกเป็น $c_0×c_1×k_1$ ชั้นที่ 2 เป็น $c_1×c_2×k_2$

ส่วนไบแอสจะมีจำนวนเท่ากับจำนวนช่องของข้อมูลขาออก เป็นค่าพารามิเตอร์ที่เอาไว้บวกใส่ทุกค่าในช่องนั้นอีกทีตอนท้ายสุด

สมมุติว่าเรามีข้อมูลของการวัดค่าอะไรบางอย่างที่เปลี่ยนแปลงไปตามเวลา โดยวัดค่าที่เวลา t=1 ไปจนถึง t=20 มีข้อมูลอยู่ 10 ตัว วาดเป็นกราฟได้ดังนี้



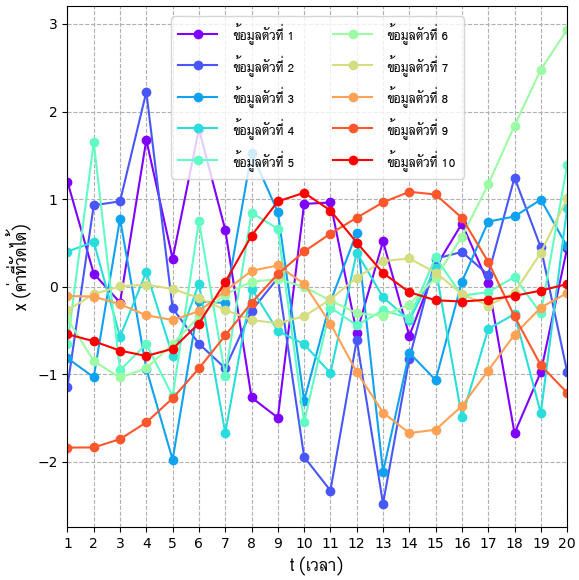
จะเห็นว่าใน 10 เส้นนี้มีความแตกต่างกันแบ่งเป็น ๒ กลุ่มชัดเจน คือเส้นที่ 1-5 ค่าเปลี่ยนแปลงรวดเร็ว และเส้นที่ 6-10 ค่าเปลี่ยนช้าๆ เราสามารถใช้โครงข่ายประสาทคอนโวลูชันหนึ่งมิติเพื่อวิเคราะห์แยกข้อมูลลักษณะนี้ได้

ในกรณีส่วนใหญ่แล้ว จำนวนช่องข้อมูลขาเข้าจะเป็น 1 คือเป็นข้อมูลอนุกรมเวลาเส้นเดียว

ข้อมูลเช่นในกราฟตัวอย่างนี้ก็เช่นกัน ดังนั้นในที่นี้จะมีช่องเดียวคือ i=1 โดย $x^{(ι,1,t)}$ เป็นค่า $x$ ตัวที่ $ι$ ที่เวลา $t$

ความสัมพันธ์ระหว่างความยาว (สำหรับในอนุกรมเวลาคือ มี t กี่ตัว) ในของข้อมูลขาเข้าและขาออกคือ

$\begin{align} \;\;\;ความยาวขาออก = ความยาวขาเข้า - ความยาวตัวกรอง + 1 \end{align}$ ..(20.7)

เช่นถ้าขาเข้ามี 20 ช่อง ความยาวตัวกรองเป็น 3 ความยาวที่ได้ออกมาก็จะเป็น 20-3+1 = 18

เพื่อให้เข้าใจได้มากขึ้น ต่อไปจะลองวาดภาพเคลื่อนไหวแสดงการคำนวณที่เกิดขึ้น

ให้ความยาวของข้อมูลขาเข้าเป็น 7 (ในกราฟด้านบนเป็น 20 แต่ในที่นี้ขอวาดแค่ 7 เพื่อความง่าย) สมมุติว่าในชั้นที่ 1 มีจำนวนช่องข้อมูลขาเข้า $c_0=1$ จำนวนช่องข้อมูลขาออก $c_1=3$ และความยาวตัวกรอง $k_1=3$

ถ้าข้อมูลตัวที่ $ι$ มีค่าเป็น [6,2,1,0,5,1,3] การคำนวณที่เกิดกับข้อมูลตัวที่ $ι$ อาจวาดภาพแสดงได้ดังนี้



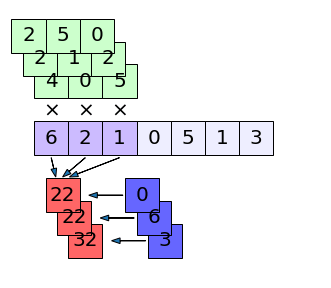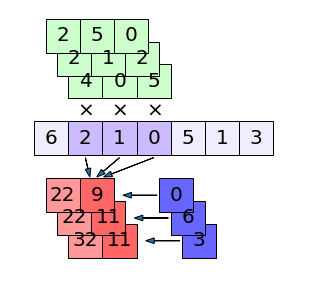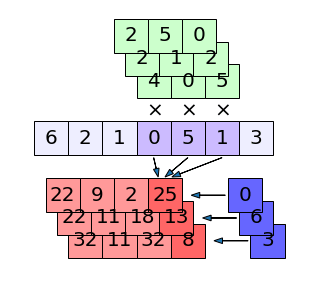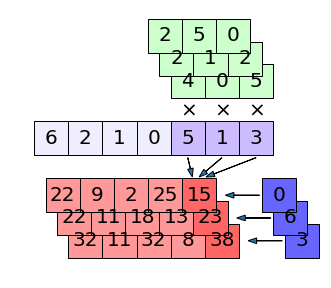
ในที่นี้ตัวกรอง (สีเขียวด้านบน) จะมี 3 ตัว เท่ากับจำนวนช่องขาออก โดยแต่ละตัวมีค่าน้ำหนัก w แยกกันอยู่ (ค่าในช่องเขียว) ตัวกรองหนึ่งมี 3 ค่า ดังนั้นรวมทั้งหมดจะเห็นว่ามีพารามิเตอร์ w ทั้งหมด 3×3=9 ตัว

แต่ละตัวกรองจะมีการคำนวณแยกกันไปโดยต่างก็คูณกับค่าในข้อมูลส่วนที่วิ่งไปถึง (สีม่วงเข้ม) แล้วก็บวกกับค่าไบแอส (ช่องสีน้ำเงินทางขวาของสีแดงที่มีลูกศรชี้ไปทางซ้าย)

ผลลัพธ์ที่ได้จากคนละตัวกรองก็จะแยกกันไม่ได้เกี่ยวข้องอะไรกัน

ดังนั้นผลที่ได้ก็จะออกมาเป็นข้อมูลความยาว 5 ทั้งหมด 3 ช่อง (สีแดงด้านล่าง) ซึ่งจะถูกนำไปใช้เป็นข้อมูลขาเข้าของชั้นที่ 2 ต่อไป

ต่อมาสำหรับในชั้นที่ 2 จะซับซ้อนขึ้นมาอีกเพราะค่าต้องคำนวณจากหลายช่อง ไม่ได้มีแค่ช่องเดียว

การคำนวณในชั้นที่ 2 อาจวาดเป็นภาพได้ดังนี้ โดยค่าข้อมูลขาออกจำนวน 5×3=15 ตัวที่ได้เป็นสีแดงในชั้นแรก ก็จะเป็นค่าป้อนเข้าของชั้นที่ 2 (สีม่วง)



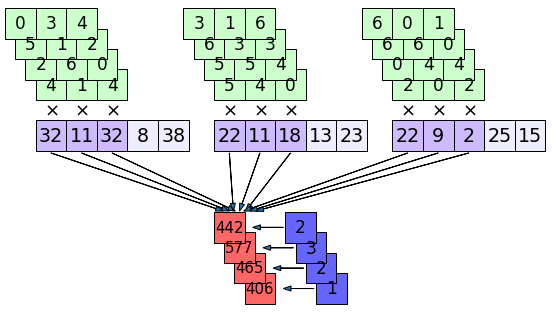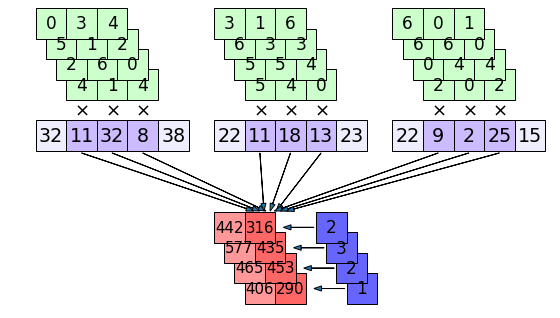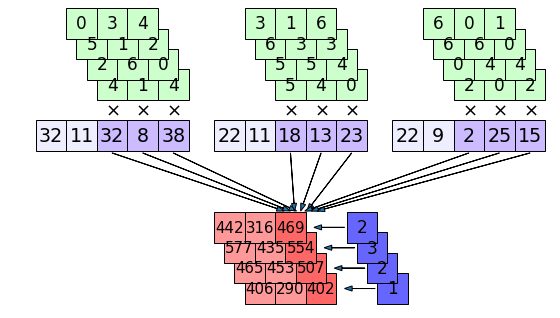
ในที่นี้จำนวนค่าพารามิเตอร์ในตัวกรองทั้งหมดก็เท่ากับจำนวนสี่เหลี่ยมเขียวในภาพ ก็คือ 3×4×3=36

ค่าที่คำนวณจากแต่ละช่องจะถูกนำมาบวกรวมกันทั้งหมด แล้วก็นำมาบวกด้วยค่าไบแอส (ช่องน้ำเงินทางขวา) อีกที จึงคำนวณออกมาได้เป็นค่าในช่องสีแดงด้านล่าง

จะเห็นว่าการคำนวณภายในชั้นคอนโวลูชันค่อนข้างซับซ้อนขึ้นเมื่อเทียบกับการคำนวณเชิงเส้น (ดูบทที่ ๗)

เพื่อให้เห็นภาพว่าคล้ายกันหรือต่างกันอย่างไร ลองมาเทียบกับการคำนวณเชิงเส้นดังที่เกิดขึ้นในสมการ (20.3) และ (20.4) ดู ซึ่งเขียนได้เป็นดังนี้

$\begin{align} a_3^{(ι,j)} &= \sum_{i=1}^{m_2} w_3^{(i,j)}h_2^{(ι,i)} + b_3^{(j)} \end{align}$ ..(20.8)

$\begin{align} a_4^{(ι,j)} &= \sum_{i=1}^{m_3} w_4^{(i,j)}h_3^{(ι,i)} + b_4^{(j)} \end{align}$ ..(20.9)

ลองเปรียบเทียบกับสมการ (20.5) กับ (20.6) จะเห็นว่ามีส่วนไหนหายไป

จะเห็นว่าข้อแตกต่างคือการคำนวณเชิงเส้นไม่มีส่วนของตัวกรองเหมือนอย่างชั้นคอนโวลูชัน

แต่ค่าไบแอส b นั้นจะมีเป็นจำนวนเท่ากับจำนวนเซลล์ขาออก เช่นเดียวกับที่ในชั้นคอนโวลูชันมีค่าไบแอส b เท่ากับจำนวนช่องขาออก

ในที่นี้ $m_3,m_4$ คือจำนวนเซลล์ขาออกของชั้นที่ 3 และ 4





การเลื่อนข้ามในระหว่างคำนวณคอนโวลูชัน

ต่อมาจะแสดงถึงตัวเลือกปรับแต่งที่สำคัญภายในชั้นคอนโวลูชัน โดยเริ่มจากเรื่องของขนาดการเลื่อน (stride) ในแต่ละการคำนวณ

ในการคำนวณชั้นคอนโวลูชัน บางครั้งอาจจะไม่ได้แค่มีการเลื่อนไปทีละช่อง แต่อาจเลื่อนข้ามหลายช่อง ซึ่งจะทำให้การคำนวณลดลงและผลที่ได้จะทำให้ได้จำนวนช่องลดลง

เมื่อพิจารณาจำนวนที่เลื่อนไปด้วย ความยาวที่ได้ก็จะเป็น

$\begin{align} \;\;\;ความยาวขาออก = \frac{ความยาวขาเข้า-ความยาวตัวกรอง}{ความยาวที่เลื่อนในแต่ละครั้ง} + 1 \end{align}$ ..(20.10)

ในที่นี้หากหารแล้วมีเศษก็จะปัดลงให้เป็นจำนวนเต็ม

เช่นในรูปนี้ (10-3)/2+1 = 4.5 ก็คือจะเหลือ 4 ช่อง



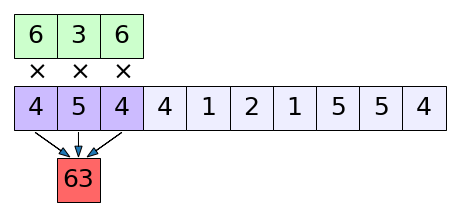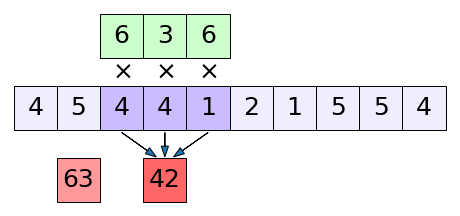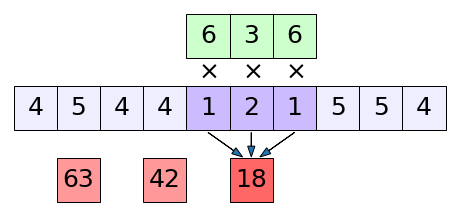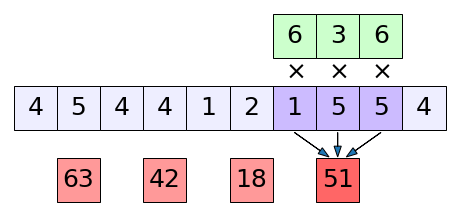
ซึ่งถ้าความยาวที่เลื่อนเป็น 1 ก็จะกลับไปสู่สมการ (20.7)

สมการ (20.5) และ (20.6) อาจเขียนใหม่เป็นกรณีทั่วไปมากขึ้นได้แบบนี้

$\begin{align} a_1^{(ι,j,t)} &= \sum_{i=1}^{c_0}\sum_{μ=1}^{k_1} w_1^{(i,j,μ)}x^{(ι,i,s_1(t-1)+μ)} + b_1^{(j)} \end{align}$ ..(20.11)

$\begin{align} a_2^{(ι,j,t)} &= \sum_{i=1}^{c_1}\sum_{μ=1}^{k_2} w_2^{(i,j,μ)}h_1^{(ι,i,s_2(t-1)+μ)} + b_2^{(j)} \end{align}$ ..(20.12)

ในที่นี้ $s_1,s_2$ คือจำนวนช่องที่เลื่อนในแต่ละครั้งของชั้นที่ 1 และ 2 หาก $s_1=1,s_2=1$ ก็จะกลับไปสู่สมการ (20.5) และ (20.6)




การเติมขอบก่อนเริ่มทำการคอนโวลูชัน

ต่อมาส่วนที่สำคัญอีกเรื่องคือการเติมขอบ (padding)

ในโครงข่ายประสาทเทียมแบบคอนโวลํชันนั้น บ่อยครั้งที่จะเห็ฯว่ามีการเติมขอบให้ข้อมูลยาวขึ้นโดยใส่ค่า 0 ลงไปก่อนที่จะเริ่มทำการคอนโวลูชัน

การเติมขอบก็ทำได้ง่ายๆโดยใส่ค่า 0 เพิ่มเข้ามาหน้าหลัง เช่นเมื่อเติมขอบข้างละ 2 ก็จะเป็นดังในรูปนี้



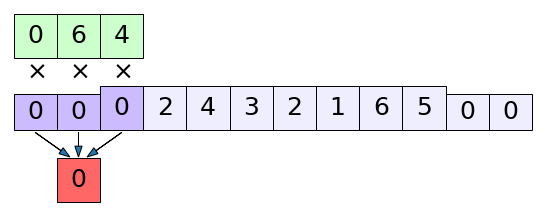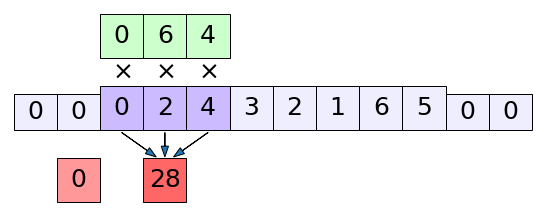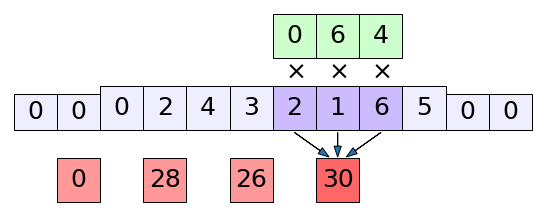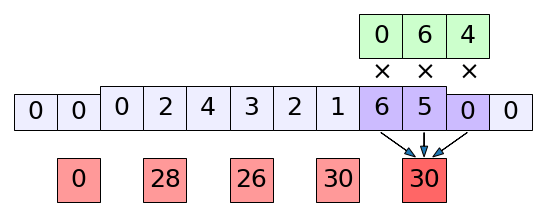
ส่วนความยาวของข้อมูลขาออกที่ได้ก็เขียนเพิ่มขึ้นมาจากสมการ (20.10) เป็น

$\begin{align} \;\;\;ความยาวขาออก = \frac{ความยาวขาเข้า-ความยาวตัวกรอง+จำนวนขอบที่เติมต่อข้าง×2}{ความยาวที่เลื่อนในแต่ละครั้ง} + 1 \end{align}$ ..(20.13)

เช่นดังในรูปนี้ (8-3+2×2)/2 + 1= 5.5 ตัดเศษทิ้งก็จะเท่ากับได้ค่าออกมา 5 ตัว

บ่อยครั้งที่การเติมขอบจะทำเพื่อชดเชยให้ความยาวชั้นที่ออกมากเท่ากับที่ป้อนเข้า เช่นถ้าตัวกรองมีความยาวเป็น 3 เลื่อนทีละ 1 ก็เติมขอบลงไปข้าง 1 ก็จะได้เท่าเดิม

$\;\;\;ความยาวของชั้นที่ออกมา = ความยาวชั้นป้อนเข้า-3+1×2+1 = ความยาวชั้นป้อนเข้า$




ชั้นบ่อรวมสูงสุด

ในโครงสร้างของโครงข่ายประสาทแบบคอนโวลูชันมักเติมชั้นบ่อรวมสูงสุด (maxpool) ไว้หลังจากชั้นคอนโวลูชัน

การทำงานของชั้นนี้ง่ายๆก็คือจับกลุ่มแล้วคัดเลือกเอาแค่ตัวที่มีค่าสูงกว่าออกมา

ตัวอย่างเช่นเมื่อจับกลุ่มเอาตัวที่ติดกันเป็นกลุ่มละ ๒​ ตัวก็เป็นแบบนี้



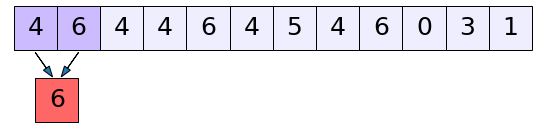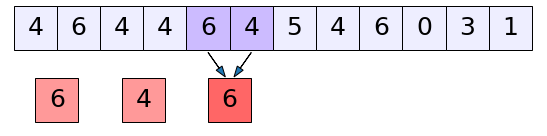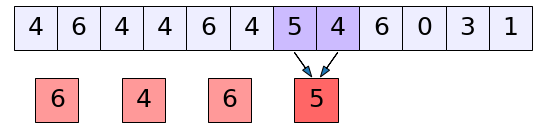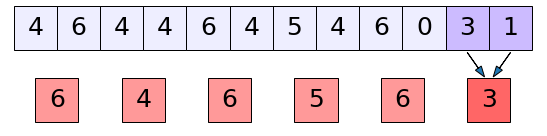
$\begin{align} ความยาวของชั้นที่ออกมา = \frac{ความยาวของชั้นป้อนเข้า}{จำนวนในแต่ละกลุ่ม} \end{align}$ ..(20.13)

จำนวนในแต่ละกลุ่มนั้นที่จริงก็เทียบไดักับความยาวตัวกรองของชั้นคอนโวลูชันนั่นเอง

ดังนั้นชั้นบ่อรวมสูงสุดนั้นดูเผินๆแล้วจะคล้ายชั้นคอนโวลูชัน แต่ในนี้ไม่มีการคำนวนใดๆ แค่ทำการคัดเลือกเอาตัวที่ค่าสูงกว่าเท่านั้น

อีกทั้งชั้นบ่อรวมสูงสุดไม่มีพารามิเตอร์ใดๆด้วย ซึ่งต่างจากชั้นคอนโวลูชันที่มีพารามิเตอร์น้ำหนัก w และไบแอส b




การเขียนคลาสของชั้นคอนโวลูชันหนึ่งมิติ

หลังจากเข้าในหลักการคำนวณภายในชั้นคอนโวลูชันแล้ว ได้เวลาลองเขียนโค้ดขึ้นมา โดยจะสร้างเป็นคลาสของชั้นคอนโวลูชัน แบบเดียวกับที่ทำในบทที่ ๑๑

โค้ดสร้างคลาสชั้นคอนโวลูชันหนึ่งมิติ

ก่อนอื่น ให้ทำการเรียกคลาสที่จำเป็นต้องใช้ในบทนี้จาก unagi.py พร้อมทั้ง numpy

import numpy as np
from unagi import Chan,Param

คลาสคอนโวลูชันเขียนได้เป็น

class Conv1d(Chan):
    def __init__(self,m0,m1,kk,st=1,pad=0,sigma=1):
        '''
        m0 : จำนวนช่องขาเข้า
        m1 : จำนวนช่องขาออก
        kk : ความยาวตัวกรอง
        st : ความยาวการเลื่อน
        pad : เติมของเพิ่มยาวข้างละ
        sigma : ส่วนเบี่ยงเบนมาตรฐานของค่าสุ่มเริ่มต้นของพารามิเตอร์น้ำหนัก
        '''
        # พารามิเตอร์ตัวแรกคือน้ำหนักในแต่ละช่อง มีจำนวน [m1,m0,kk] ให้เริ่มต้นด้วยค่าสุ่มโดยแจกแจงแบบปกติโดยส่วนเบียงเบนมาตรฐานเป็นตามค่า sigma
        # อีกตัวคือไบแอส มีจำนวนเป็น m1 ให้เริ่มต้นจาก 0
        self.param = [Param(np.random.normal(0,sigma,[m1,m0,kk])),
                      Param(np.zeros(m1))]
        self.st = st
        self.pad = pad
    
    def pai(self,X):
        # เติมขอบ ถ้า pad>0
        X = np.pad(X,[(0,0),(0,0),(self.pad,self.pad)],'constant')
        # ขนาดในแต่ละมิติของพารามิเตอร์ w (จำนวนช่องขาออก, จำนวนช่องขาเข้า, ความยาวตัวกรอง)
        m1,m0,kk = self.param[0].kha.shape
        # ขนาดของข้อมูลขาเข้า (จำนวนข้อมูล, จำนวนช่องขาเข้า, ความยาวข้อมูลขาเข้าหลังเติมขอบ)
        n,m0_,k0 = X.shape
        # จำนวนช่องของข้อมูลขาเข้าควรเท่ากับจำนวนช่องของพารามิเตอร์ w ขาเข้า
        assert m0_==m0
        # ความยาวข้อมูลขาออก
        k1 = int((k0-kk)/self.st)+1
        # สร้างอาเรย์ของข้อมูลขาเข้าที่ปรับรูปใหม่เพื่อให้ทำการคำนวณสะดวก
        X_ = np.zeros([n,m0,kk,k1])
        for i in range(kk):
            X_[:,:,i,:] = X[:,:,i:i+k1*self.st:self.st]
        X_ = X_.transpose(0,3,1,2).reshape(-1,m0*kk)
        w = self.param[0].kha.reshape(m1,-1).T
        b = self.param[1].kha
        # คำนวณค่าข้อมูลขาออก
        a = np.dot(X_,w) + b
        a = a.reshape(n,k1,-1).transpose(0,2,1)
        self.ruprang = n,m1,m0,kk,k0,k1
        self.X_ = X_
        return a ̰
    
    def yon(self,g):
        # จำนวนข้อมูล, จำนวนช่องขาเข้า, จำนวนช่องขาออก, ความยาวตัวกรอง, ความยาวข้อมูลขาเข้า, ความยาวข้อมูลขาออก
        n,m1,m0,kk,k0,k1 = self.ruprang
        g = g.transpose(0,2,1).reshape(-1,m1)
        w = self.param[0].kha.reshape(m1,-1).T
        self.param[0].g = np.dot(self.X_.T,g).transpose(1,0).reshape(m1,m0,kk)
        self.param[1].g = g.sum(0)
        gX_ = np.dot(g,w.T)
        gX_ = gX_.reshape(-1,k1,m0,kk).transpose(0,2,3,1)
        gX = np.zeros([n,m0,k0+self.pad*2])
        for i in range(kk):
            gX[:,:,i:i+k1*self.st:self.st] += gX_[:,:,i,:]
        return gX[:,:,self.pad:k0-self.pad]

การเขียนคลาสของชั้นบ่อรวมสูงสุดหนึ่งมิติ

ต่อมาเป็นโค้ดสร้างคลาสชั้นบ่อรวมสูงสุดหนึ่งมิติ

ลักษณะจะคล้ายๆกับชั้นคอนโวลูชัน แต่จะง่ายกว่าเพราะไม่มีพารามิเตอร์

class MaxP1d(Chan):
    def __init__(self,kk,st=None):
        '''
        kk : ความยาวตัวกรอง
        st : ความยาวการเลื่อน (ถ้าไม่กำหนด ก็ให้เท่ากับความยาวตัวกรอง)
        '''
        self.kk = kk
        if(st==None):
            self.st = self.kk
        else:
            self.st = st
    
    def pai(self,X):
        # ขนาดของข้อมูลขาเข้า (จำนวนข้อมูล, จำนวนช่องขาเข้า, ความยาวข้อมูลขาเข้า)
        n,m,k0 = X.shape
        k1 = int((k0-self.kk)/self.st)+1
        X_ = np.zeros([n,m,self.kk,k1])
        for i in range(self.kk):
            X_[:,:,i,:] = X[:,:,i:i+k1*self.st:self.st]
        X_ = X_.transpose(0,3,1,2).reshape(-1,self.kk)
        self.argmax = X_.argmax(1)
        self.ruprang = n,m,k0,k1
        return X_.max(1).reshape(n,k1,m).transpose(0,2,1)
    
    def yon(self,g):
        # จำนวนข้อมูลขาเข้า, จำนวนช่องข้อมูลขาเข้า, ความยาวข้อมูลขาเข้า, ความยาวข้อมูลขาออก
        n,m,k0,k1 = self.ruprang
        g = g.transpose(0,2,1)
        gX_ = np.zeros([g.size,self.kk])
        gX_[np.arange(len(self.argmax)),self.argmax] = g.flatten()
        gX_ = gX_.reshape(-1,k1,m,self.kk).transpose(0,2,3,1)
        gX = np.zeros([n,m,k0])
        for i in range(self.kk):
            gX[:,:,i:i+k1*self.st:self.st] += gX_[:,:,i,:]
        return gX

การเขียนคลาสของชั้นตัวเปลี่ยนรูป

อีกส่วนประกอบหนึ่งที่สำคัญของโครงข่ายประสาทคอนโวลูชันก็คือชั้นที่คั่นระหว่างส่วนคอนโวลูชันและส่วนเชิงเส้น ซึ่งเราจำเป็นต้องปรับเปลี่ยนรูปร่างมิติของข้อมูลไป

เพราะรูปร่างของข้อมูลที่ออกมาจากชั้นคอนโวลูชันจะเป็น 3 มิติ (จำนวนข้อมูล, จำนวนช่อง, ความยาวตัวกรอง)

ในขณะที่ชั้นเชิงเส้นข้อมูลป้อนเข้าต้องการข้อมูลแค่ 2 มิติ (จำนวนข้อมูล, จำนวนเซลล์ขาเข้า)

ดังนั้นต้องทำการเปลี่ยนรูป โดยเอาค่าจากทุกช่องในทุกตัวกรองมาเรียงต่อกันเป็นแถวเดียว

ก็จะได้ว่า

$\;\;\;จำนวนเซลล์เข้าชั้นเชิงเส้น = \begin{align} จำนวนช่องขาออกจากชั้นคอนโวลูชัน\\×\\ความยาวตัวกรอง\end{align}$

เขียนโค้ดสร้างคลาสของชั้นเปลี่ยนรูปได้ดังนี้

class Plianrup(Chan):
    def __init__(self,*rupmai):
        self.rupmai = rupmai
        
    def pai(self,x):
        self.rupdoem = x.shape
        return x.reshape(self.rupdoem[0],*self.rupmai)
    
    def yon(self,g):
        return g.reshape(*self.rupdoem)

ในที่นี้ rupmai คือรูปร่างของข้อมูลที่ต้องการจะได้ออกมา แต่ไม่ต้องใส่มิติแรกซึ่งคือมิติของข้อมูลแยกแต่ละตัว ให้มิติแรกเท่าเดิม

สำหรับการบีบให้เหลือแค่มิติเดียว (รวมมิติจำนวนข้อมูลเป็นสองมิติ) ก็ให้เติมเป็น -1 เป็น Plianrup(-1)




ตัวอย่างการสร้างและใช้งานโครงข่ายประสาทแบบคอนโวลูชันหนึ่งมิติ

หลังจากรู้วิธีการสร้างคลาสของชั้นต่างๆที่จำเป็นในโครงข่ายประสาทเทียมแบบคอนโวลูชันแล้ว คราวนี้จะนำชั้นต่างๆเหล่านั้นมาประกอบกันเป็นโครงข่าย แล้วใช้งานเพื่อวิเคราะห์ข้อมูล

ในที่นี้ขอยกตัวอย่าง โดยสมมุติว่าเรามีข้อมูลชุดหนึ่งเป็นค่าอะไรบางอย่างที่เปลี่ยนแปลงไปตามเวลา โดยวัดค่าที่เวลา t=1 ไปจนถึง t=200 ได้ผลออกมาคือ ก. ข. ค. ซึ่งมีความเร็วในการเปลี่ยนแปลงต่างกันไป นำผลของค่าทั้ง ๓ กลุ่มส่วนหนึ่งมาวาดกราฟได้เป็นดังนี้



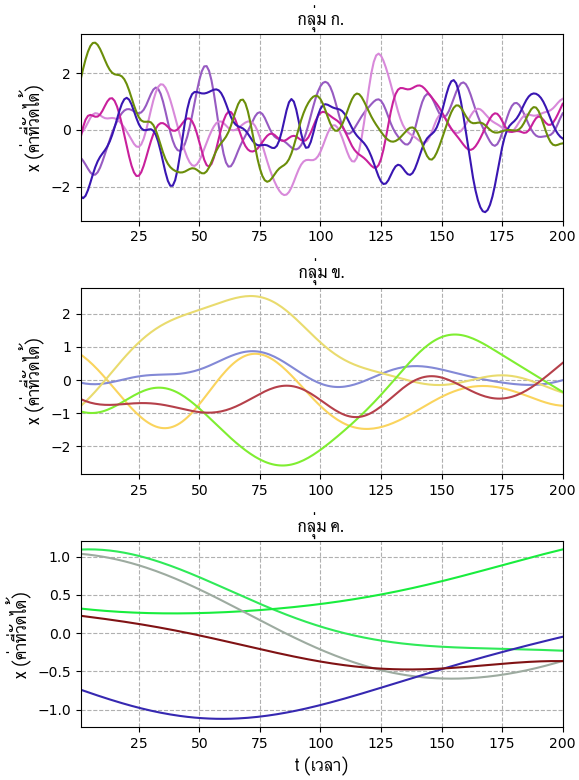
(วิธีการสร้างข้อมูลแบบนี้จะไม่พูดถึงในรายละเอียด หากสนใจอาจอ่านได้ใน https://phyblas.hinaboshi.com/20180525)

เราสามารถใช้โครงข่ายประสาทแบบคอนโวลูชันเพื่อทำการจำแนกข้อมูลกราฟ ๓ กลุ่มนี้ได้

คลาสของชั้นต่างๆที่จำเป็นได้ใส่รวมไว้ใน unagi.py แล้ว รวมทั้งชั้นคอนโวลูชัน ชั้นบ่อรวมสูงสุด และชั้นเปลี่ยนรูปด้วย สามารถเรียกใช้ (โดย from unagi import) คลาสส่วนประกอบที่จำเป็นเพื่อสร้างโครงข่ายประสาทคอนโวลูชันในที่นี้ได้เลย

ลองสร้างโครงข่ายประสาทคอนโวลูชันที่ประกอบไปด้วยชั้นคอนโวลูชัน ๒ ชั้น และชั้นเชิงเส้น ๒ ชั้น และนำมาใช้วิเคราะห์จำแนกข้อมูลอนุกรมเวลา ๓ กลุ่ม ดังนี้

import numpy as np
import matplotlib.pyplot as plt
from unagi import Affin,Relu,Softmax_entropy,ha_1h,Adam,Conv1d,MaxP1d,Plianrup

# โครงข่ายประสาทคอนโวลูชัน
class PrasatConvo:
    def __init__(self,eta):
        self.chan = []
        # ชั้น 1 คอนโวลูชัน (ช่องขาเข้า 1, ช่องขาออก 16, ความยาวตัวกรอง 29)
        self.chan.append(Conv1d(1,16,29,sigma=0.1))
        self.chan.append(Relu())
        self.chan.append(MaxP1d(2))
        # ชั้น 2 คอนโวลูชัน (ช่องขาเข้า 16, ช่องขาออก 8, ความยาวตัวกรอง 21)
        self.chan.append(Conv1d(16,8,21,sigma=0.1))
        self.chan.append(Relu())
        self.chan.append(MaxP1d(2))
        # ใส่ชั้นสำหรับทำการเปลี่ยนรูปก่อนไปเข้าชั้นเชิงเส้น
        self.chan.append(Plianrup(-1))
        # ชั้น 3 เชิงเส้น (เซลล์ขาเข้า 264, เซลล์ขาออก 64)
        self.chan.append(Affin(264,64,np.sqrt(2./264)))
        self.chan.append(Relu())
        # ชั้น 4 (เซลล์ขาเข้า 64, เซลล์ขาออก 3)
        self.chan.append(Affin(64,3,np.sqrt(2./64)))
        self.chan.append(Softmax_entropy())
        
        self.opt = Adam(self.param(),eta=eta)
    
    def rianru(self,X,z,X_truat,z_truat,n_thamsam=100,n_batch=50,ro=0):
        n = len(z)
        Z = ha_1h(z,3)
        self.entropy = []
        self.khanaen_fuek = []
        self.khanaen_truat = []
        khanaen_sungsut = 0
        for o in range(n_thamsam):
            lueak = np.random.permutation(n)
            for i in range(0,n,n_batch):
                Xb = X[lueak[i:i+n_batch]]
                Zb = Z[lueak[i:i+n_batch]]
                entropy = self.ha_entropy(Xb,Zb)
                entropy.phraeyon()
                self.opt()
            entropy,khanaen_fuek = self.ha_entropy(X_fuek,Z,ao_khanaen=1)
            khanaen_truat = self.ha_khanaen(X_truat,z_truat)
            self.entropy.append(entropy.kha)
            self.khanaen_fuek.append(khanaen_fuek)
            self.khanaen_truat.append(khanaen_truat)
            print('รอบที่ %d. เอนโทรปี=%.2e, ทำนายข้อมูลฝึกแม่น=%.3f, ทำนายข้อมูลตรวจสอบแม่น=%.3f'%(o,entropy.kha,khanaen_fuek,khanaen_truat))
            
            if(khanaen_truat>khanaen_sungsut):
                khanaen_sungsut = khanaen_truat
                maiphoem = 0
            else:
                maiphoem += 1
            
            if(ro>0 and maiphoem>=ro):
                break
    
    def ha_entropy(self,X,Z,ao_khanaen=0):
        for c in self.chan[:-1]:
            X = c(X)
        if(ao_khanaen):
            return self.chan[-1](X,Z),(X.kha.argmax(1)==Z.argmax(1)).mean()
        return self.chan[-1](X,Z)
    
    def ha_khanaen(self,X,z):
        return (self.thamnai(X)==z).mean()
    
    def param(self):
        p = []
        for c in self.chan:
            if(hasattr(c,'param')):
                p.extend(c.param)
        return p
    
    def thamnai(self,X):
        for c in self.chan[:-1]:
            X = c(X)
        return X.kha.argmax(1)

# สร้างข้อมูลตัวอย่าง
def cov(x,s):
    x1,x2 = np.meshgrid(x,x)
    return np.exp(-0.5*((x1-x2)/s)**2)
# จำนวนข้อมูลแต่ละกลุ่ม
n0,n1,n2 = 240,50,110
n = n0+n1+n2 # จำนวนข้อมูลทั้งหมด
nt = 200 # ความยาวของข้อมูลอนุกรมเวลา
t = np.arange(nt)
# สร้างข้อมูลทั้ง 3 กลุ่ม แล้วเอามาผสมกัน
# กลุ่ม ก.
X0 = np.random.multivariate_normal(np.zeros(nt),cov(t,5),n0)
# กลุ่ม ข.
X1 = np.random.multivariate_normal(np.zeros(nt),cov(t,25),n1)
# กลุ่ม ค.
X2 = np.random.multivariate_normal(np.zeros(nt),cov(t,100),n2)
# ผสมรวม
X = np.vstack([X0,X1,X2])
# คำตอบจริง ว่าเป็นกลุ่มที่ 0,1,2
z = np.array([0]*n0+[1]*n1+[2]*n2)

X = X.reshape(-1,1,nt)
# ทำการสุ่มสลับลำดับข้อมูลแล้วแบ่งเป็นส่วนฝึกฝนกับส่วนตรวจสอบ
sumlueak = np.random.permutation(n)
n_fuek = int(n*0.8)
X_fuek,X_truat = X[sumlueak[:n_fuek]],X[sumlueak[n_fuek:]]
z_fuek,z_truat = z[sumlueak[:n_fuek]],z[sumlueak[n_fuek:]]
# สร้างโครงข่ายประสาท
prasat = PrasatConvo(eta=0.005)
# เริ่มทำการเรียนรู้
prasat.rianru(X_fuek,z_fuek,X_truat,z_truat,n_thamsam=200,n_batch=64,ro=10)

# วาดกราฟแสดงความเปลี่ยนแปลงค่าเอนโทรปีและคะแนนในแต่ละขั้น
plt.figure(figsize=[5,6],dpi=100)
plt.subplot(211)
plt.semilogy()
plt.plot(prasat.entropy,'b') # วาดกราฟค่าเอนโทรปีที่บันทึกไว้ระหว่างการฝึก
plt.title('เอนโทรปี',family='Tahoma',size=13)
plt.grid(ls='--')

plt.subplot(212)
# วาดกราฟค่าคะแนนฝึกของข้อมูลชุดฝึกและชุดตรวจสอบที่บันทึกไว้ระหว่างฝึก
plt.plot(prasat.khanaen_fuek,'m')
plt.plot(prasat.khanaen_truat,'g')
plt.title('คะแนน',family='Tahoma',size=13)
plt.legend(['ข้อมูลฝึก','ข้อมูลตรวจสอบ'],prop={'family':'Tahoma','size':14})
plt.grid(ls='--')
plt.tight_layout()
plt.show()

ผลที่ได้



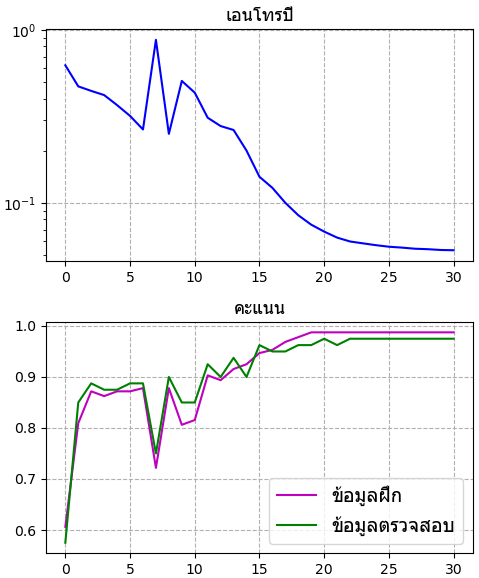
ในที่นี้ความยาวข้อมูลขาเข้าเป็น 200 เมื่อผ่านชั้นคอนโวลูชันที่ 1 ซึ่งมีขนาดตัวกรองเป็น 29 ก็จะกลายเป็น 200-29+1=172 และผ่านชั้นบ่อรวมขนาด 2 ก็เป็น 172/2=86

จากผ่านชั้นคอนโวลูชันที่ 2 ซึ่งมีขนาดตัวกรองเป็น 21 ก็จะกลายเป็น 86-21+1=66 และผ่านชั้นบ่อรวม 2 ก็เป็น 66/2=33

และเนื่องจากชั้นที่ 2 นี้มีจำนวนช่องขาออกเป็น 8 ดังนั้นเมื่อแปลงเป็นมิติเดียวเพื่อเป็นค่าป้อนเข้าให้ชั้นที่ 3 ซึ่งเป็นชั้นเชิงเส้นก็จะได้ว่ามีค่าขาเข้าเป็น 8×33=264 ตัว

ส่วนจำนวนเซลล์ข้อมูลขาออกของชั้นที่ 4 จะต้องเป็น 3 เพราะในที่นี้เราต้องการวิเคราะห์แยกแยะข้อมูลออกเป็น ๓ กลุ่ม




สรุปท้ายบท

ในบทนี้ได้กล่าวถึงหลักการของโครงข่ายประสาทแบบคอนโวลูชันในเบื้องต้น โดยเริ่มจากกรณีหนึ่งมิติ

ความจริงแล้วเรื่องนี้ค่อนข้างซับซ้อนและเนื้อหายังมีรายละเอียดยิบย่อยต่างๆอีกมากที่ไม่ได้กล่าวถึง แต่ในที่นี้แค่แนะนำเบื้องต้นให้พอเห็นภาพและสามารถเขียนโค้ดขึ้นมาได้

ตัวอย่างโค้ดในที่นี้เป็นแค่การฝึกเขียนเพื่อให้พอเห็นภาพ แต่ในการใช้งานจริงๆในทางปฏิบัติแนะนำให้ใช้มอดูลที่ถูกทำไว้ดีอยู่แล้วเช่น pytorch >> (pytorch เบื้องต้น บทที่ ๑๒ โครงข่ายประสาทเทียมแบบคอนโวลูชัน)

สำหรับในบทต่อไปบทสุดท้ายนี้จะเป็นเรื่องของโครงข่ายประสาทแบบคอนโวลูชันสองมิติ




>> อ่านต่อ บทที่ ๒๑

~ 自我介绍 ~

目录

从日本来的名言

python 模块 -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 机器学习 -- 神经网络

javascript

蒙古语

语言学

maya

概率论

与日本相关的日记

与中国相关的日记 -- 与北京相关的日记 -- 与香港相关的日记 -- 与澳门相关的日记

与台湾相关的日记

与北欧相关的日记

与其他国家相关的日记

qiita

其他日志

按类别分日志

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --MATLAB --SQL --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม --สเตเบิลดิฟฟิวชัน ---comfyui -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ -ซางะ -นางาซากิ -คุมาโมโตะ -โออิตะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ -ออสเตรเลีย ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม เรื่องแต่ง บันทึก

　 查看日志

　 最近

　 推荐日志

各月日志

找更早以前的日志

ไทย

日本語

中文