[python] แยกแยะภาพตัวเลขที่เขียนด้วยลายมือด้วยการวิเคราะห์การถดถอยโลจิสติก
เขียนเมื่อ 2017/09/22 20:52
แก้ไขล่าสุด 2021/09/28 16:42
ในตอนที่แล้วได้แนะนำให้รู้จักชุดข้อมูลตัวเลขที่เขียนด้วยลายมือของ MNIST ไป https://phyblas.hinaboshi.com/20170920

สำหรับในตอนนี้จะลองนำข้อมูลนี้มาใช้ทดสอบการแยกแยะตัวเลขดู โดยใช้วิธีที่พื้นฐานที่สุด นั่นคือการถดถอยโลจิสติกแบบมัลติโนเมียล (การถดถอยซอฟต์แม็กซ์)
รายละเอียดเรื่องการถดถอยโลจิสติกได้เขียนถึงไปมากแล้วในบทความก่อนหน้านี้ เช่น https://phyblas.hinaboshi.com/20161205
โค้ดสำหรับแบบจำลองการถดถอยโลจิสติกที่ใช้ในนี้ดัดแปลงจากในบทความก่อนๆมา
ในบทความก่อนๆที่เคยเขียนถึงนั้นเรามักใช้กับข้อมูลที่มีจำนวนตัวแปรต้นแค่ ๒ แต่สำหรับข้อมูล MNIST นี้ ตัวแปรต้นมีมากถึง ๗๘๔ ตัว
แม้จะมีตัวแปรต้น (จำนวนมิติ) มากขนาดนั้น แต่ก็สามารถใช้วิธีเดียวกันในการแก้ปัญหาได้ แนวคิดก็เหมือนกัน คือสร้างโปรแกรมให้มันเรียนรู้เพื่อปรับค่ำน้ำหนักของแต่ละตัวแปร
แนวคิดในการออกแบบสร้างเป็นดังนี้
- เนื่องจากข้อมูลเดิมมีค่า 0~255 เพื่อให้เหมาะสมต่อการคำนวณจึงหารด้วย 255 ให้ค่าอยู่ระหว่าง 0~1
- จำนวนตัวแปรต้นคือ 784 ตัวแปรตาม 10 ตัว (คือผลการทายตัวเลขทั้งสิบในแบบ one-hot)
- ค่าเสียหายใช้เอนโทรปีไขว้
- ตั้งเงื่อนไขการหยุดทำซ้ำเป็นว่าถ้าค่าความแม่นไม่เพิ่มขึ้นเลยเกิน ๑๐ ครั้งก็ให้หยุดและใช้ค่าน้ำหนักที่ให้ค่าความแม่นสูงสุด
- เนื่องจากข้อมูลนำเข้ามีจำนวนมากและมีความหลากหลาย ควรใช้มินิแบตช์
โค้ด
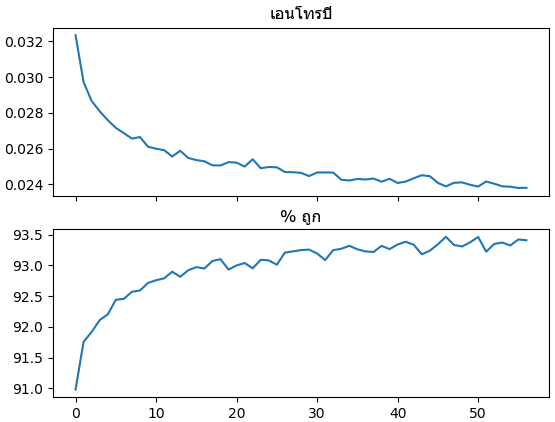
ผลที่ได้พบว่าความแม่นยำขึ้นไปได้ถึงที่ประมาณ 93% และไม่อาจสูงขึ้นไปกว่านี้แล้ว ซึ่งลองดูตัวอย่างที่คนอื่นๆทำก็พบว่าจะได้สูงสุดแค่ประมาณนั้นกันเหมือนกัน
ที่จริงแล้วการแยกภาพตัวเลขเป็นเรื่องที่ต้องพิจารณาอย่างซับซ้อนเกินกว่าที่แค่ใช้การถดถอยโลจิสติกธรรมดาแล้วจะทำได้ดีเพียงพอ
ระบบการคิดของการถดถอยโลจิสติกที่ใช้การคำนวณแค่ชั้นเดียวแบบนี้ค่อนข้างเข้าใจได้ไม่ยาก คือโดยทั่วไปแล้วจะพิจารณาจากว่าช่องไหนมีการเขียนแล้วจะมีโอกาสที่จะเป็นตัวเลขไหนมากกว่า เช่น "เลข 0 ต้องมีรอบๆแต่ต้องไม่มีตรงกลาง"
ลองดูค่าน้ำหนักของเลข 0 ที่ได้เป็นผลลัพธ์ออกมา
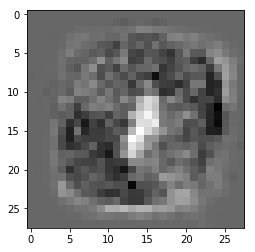
ในที่นี้สีดำคือช่องที่ถ้าถูกเขียนแล้วจะมีโอกาสเป็น 0 มาก ส่วนสีขาวคือถ้าถูกเขียนจะมีโอกาสเป็น 0 น้อย
จากนั้นลองดูตัวเลขอื่นๆที่เหลือ

แต่ละภาพก็บอกแนวโน้มได้คร่าวๆว่าเวลาคนเราเขียนตัวเลขต่างๆนั้น ดินสอมักจะถูกขีดที่ตำแหน่งไหนมากหรือน้อย
แต่ในความเป็นจริงแล้วระบบการคิดของมนุษย์เราไม่ควรจะง่ายๆแค่นั้น เช่นว่าเลข 0 บางครั้งอาจถูกเขียนเบี้ยวมาอยู่ทางขวามากหน่อย จนเส้นไปพาดผ่านตรงกลาง พอมีกรณีแบบนี้ขึ้นโอกาสทายผิดก็มีสูง
ปกติควรพิจารณาว่าเลข 0 เป็นสิ่งที่มีขอบและรูตรงกลาง ตรงไหนอาจจะเป็นขอบหรือรูก็ไม่รู้ แม้รูจะมักอยู่ตรงกลางสุด แต่ก็ไม่เสมอไป
ดังนั้นจำเป็นต้องสามารถคิดในลักษณะที่ว่า "ถ้าตรงนี้มีการเขียนแล้วตรงนั้นต้องไม่มีถึงจะควรเป็นเลขนี้ แต่ถ้าตรงนี้ไม่มีก็ควรต้องมีตรงนี้"
ซึ่งระบบที่เขียนขึ้นข้างต้นนี้จะยังไม่สามารถพิจารณาอะไรซับซ้อนหลายตลบแบบนั้นได้เพราะมีแค่ชั้นเดียว
อีกทั้งข้อมูลของทั้ง 784 ช่องถูกป้อนในลักษณะที่เป็นมิติเดียว แถมไม่มีอะไรเป็นตัวบอกว่าช่องไหนอยู่ติดกัน ช่องที่ 1,2,3 ก็เป็นตัวแปรต้นต้นตัวนึงเหมือนๆกัน ไม่ได้ถูกพิจารณาว่าช่อง 2 กับช่อง 1 มีความใกล้ชิดกันมากกว่าช่อง 3 กับช่อง 1
เพื่อที่จะให้เครื่องเรียนรู้อะไรซับซ้อนขึ้น จึงจำเป็นต้องสร้างระบบการเรียนรู้ที่ซับซ้อนขึ้น
วิธีการหนึ่งที่นิยมใช้กันมากก็คือ การเอาส่วนคำนวณการถดถอยโลจิสติกมาซ้อนต่อกันเป็น ๒ ชั้นขึ้นไป ซึ่งก็คือการสร้างเครือข่ายประสาทเทียม (神经网路, neural network)
นี่ก็เป็นเรื่องที่ตั้งใจจะเขียนถึงในบทความต่อๆไป
อ้างอิง

สำหรับในตอนนี้จะลองนำข้อมูลนี้มาใช้ทดสอบการแยกแยะตัวเลขดู โดยใช้วิธีที่พื้นฐานที่สุด นั่นคือการถดถอยโลจิสติกแบบมัลติโนเมียล (การถดถอยซอฟต์แม็กซ์)
รายละเอียดเรื่องการถดถอยโลจิสติกได้เขียนถึงไปมากแล้วในบทความก่อนหน้านี้ เช่น https://phyblas.hinaboshi.com/20161205
โค้ดสำหรับแบบจำลองการถดถอยโลจิสติกที่ใช้ในนี้ดัดแปลงจากในบทความก่อนๆมา
ในบทความก่อนๆที่เคยเขียนถึงนั้นเรามักใช้กับข้อมูลที่มีจำนวนตัวแปรต้นแค่ ๒ แต่สำหรับข้อมูล MNIST นี้ ตัวแปรต้นมีมากถึง ๗๘๔ ตัว
แม้จะมีตัวแปรต้น (จำนวนมิติ) มากขนาดนั้น แต่ก็สามารถใช้วิธีเดียวกันในการแก้ปัญหาได้ แนวคิดก็เหมือนกัน คือสร้างโปรแกรมให้มันเรียนรู้เพื่อปรับค่ำน้ำหนักของแต่ละตัวแปร
แนวคิดในการออกแบบสร้างเป็นดังนี้
- เนื่องจากข้อมูลเดิมมีค่า 0~255 เพื่อให้เหมาะสมต่อการคำนวณจึงหารด้วย 255 ให้ค่าอยู่ระหว่าง 0~1
- จำนวนตัวแปรต้นคือ 784 ตัวแปรตาม 10 ตัว (คือผลการทายตัวเลขทั้งสิบในแบบ one-hot)
- ค่าเสียหายใช้เอนโทรปีไขว้
- ตั้งเงื่อนไขการหยุดทำซ้ำเป็นว่าถ้าค่าความแม่นไม่เพิ่มขึ้นเลยเกิน ๑๐ ครั้งก็ให้หยุดและใช้ค่าน้ำหนักที่ให้ค่าความแม่นสูงสุด
- เนื่องจากข้อมูลนำเข้ามีจำนวนมากและมีความหลากหลาย ควรใช้มินิแบตช์
โค้ด
import numpy as np
def softmax(x):
exp_x = np.exp(x.T-x.max(1))
return (exp_x/exp_x.sum(0)).T
class ThotthoiLogistic:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam,n_batch=0,romaiphoem=10):
n = len(z)
if(n_batch==0 or n<n_batch):
n_batch = n
self.kiklum = int(z.max()+1)
z_1h = z[:,None]==range(self.kiklum)
self.w = np.zeros([X.shape[1]+1,self.kiklum])
self.entropy = []
self.thuktong = []
thukmaksut = 0 # ค่าจำนวนที่ถูกมากสุด
thukmaiphoem = 0 # นับว่าจำนวนที่ถูกไม่เพิ่มมาแล้วกี่ครั้ง
for j in range(n_thamsam):
lueak = np.random.permutation(n)
for i in range(0,n,n_batch):
Xn = X[lueak[i:i+n_batch]]
zn = z_1h[lueak[i:i+n_batch]]
phi = self.ha_softmax(Xn)
eee = (zn-phi)/len(zn)*self.eta
self.w[1:] += np.dot(eee.T,Xn).T
self.w[0] += eee.sum(0)
thukmai = self.thamnai(X)==z
thukmak = thukmai.mean()*100
if(thukmak > thukmaksut):
# ถ้าจำนวนที่ถูกมากขึ้นกว่าเดิมก็บันทึกค่าจำนวนนั้น และน้ำหนักในตอนนั้นไว้
thukmaksut = thukmak
thukmaiphoem = 0
w = self.w.copy()
else:
thukmaiphoem += 1 # ถ้าไม่ถูกมากขึ้นก็นับไว้ว่าไม่เพิ่มไปอีกครั้งแล้ว
self.thuktong += [thukmak]
self.entropy += [self.ha_entropy(X,z_1h)]
print(u'ครั้งที่ %d ถูก %.3f%% สูงสุด %.3f%% ไม่เพิ่มมาแล้ว %d ครั้ง'%(j+1,self.thuktong[-1],thukmaksut,thukmaiphoem))
if(romaiphoem!=0 and thukmaiphoem>=romaiphoem):
break # ถ้าจำนวนที่ถูกไม่เพิ่มเลย 10 ครั้งก็เลิกทำ
self.w = w # ค่าน้ำหนักที่ได้ในท้ายสุด เอาตามค่าที่ทำให้ทายถูกมากที่สุด
def thamnai(self,X):
return (np.dot(X,self.w[1:])+self.w[0]).argmax(1)
def ha_softmax(self,X):
return softmax(np.dot(X,self.w[1:])+self.w[0])
def ha_entropy(self,X,z_1h):
return -(z_1h*np.log(self.ha_softmax(X)+1e-7)).mean()
# ดึงข้อมูล MNIST
mnist = datasets.fetch_openml('mnist_784')
mnist.data = mnist.data/255. # ทำให้ค่าเป็น 0~1
np.random.seed(0)
sumriang = np.random.permutation(len(mnist.target)) # สุ่มเรียงลำดับข้อมูลใหม่
X = mnist.data[sumriang]
z = mnist.target.astype(int)[sumriang]
# เริ่มการเรียนรู้
eta = 0.24 # อัตราการเรียนรู้
n_thamsam = 1000 # จำนวนทำซ้ำสูงสุดถ้าไม่มีการหยุดเสียก่อน
n_batch = 100 # จำนวนมินิแบตช์
romaiphoem = 10 # จะให้หยุดเมื่อความแม่นยำไม่เพิ่มเกินกี่ครั้ง
tl = ThotthoiLogistic(eta)
tl.rianru(X,z,n_thamsam,n_batch,romaiphoem)
# กราฟแสดงความคืบหน้าในการเรียนรู้
ax = plt.subplot(211)
ax.set_title(u'เอนโทรปี',fontname='Tahoma')
plt.plot(tl.entropy)
plt.tick_params(labelbottom='off')
ax = plt.subplot(212)
ax.set_title(u'% ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
plt.show()ผลที่ได้พบว่าความแม่นยำขึ้นไปได้ถึงที่ประมาณ 93% และไม่อาจสูงขึ้นไปกว่านี้แล้ว ซึ่งลองดูตัวอย่างที่คนอื่นๆทำก็พบว่าจะได้สูงสุดแค่ประมาณนั้นกันเหมือนกัน

ที่จริงแล้วการแยกภาพตัวเลขเป็นเรื่องที่ต้องพิจารณาอย่างซับซ้อนเกินกว่าที่แค่ใช้การถดถอยโลจิสติกธรรมดาแล้วจะทำได้ดีเพียงพอ
ระบบการคิดของการถดถอยโลจิสติกที่ใช้การคำนวณแค่ชั้นเดียวแบบนี้ค่อนข้างเข้าใจได้ไม่ยาก คือโดยทั่วไปแล้วจะพิจารณาจากว่าช่องไหนมีการเขียนแล้วจะมีโอกาสที่จะเป็นตัวเลขไหนมากกว่า เช่น "เลข 0 ต้องมีรอบๆแต่ต้องไม่มีตรงกลาง"
ลองดูค่าน้ำหนักของเลข 0 ที่ได้เป็นผลลัพธ์ออกมา
plt.imshow(tl.w[1:,0].reshape(28,28),cmap='gray_r')
plt.show()
ในที่นี้สีดำคือช่องที่ถ้าถูกเขียนแล้วจะมีโอกาสเป็น 0 มาก ส่วนสีขาวคือถ้าถูกเขียนจะมีโอกาสเป็น 0 น้อย
จากนั้นลองดูตัวเลขอื่นๆที่เหลือ
for i in range(1,10):
plt.subplot(330+i)
plt.imshow(tl.w[1:,i].reshape(28,28),cmap='gray_r')
plt.show()
แต่ละภาพก็บอกแนวโน้มได้คร่าวๆว่าเวลาคนเราเขียนตัวเลขต่างๆนั้น ดินสอมักจะถูกขีดที่ตำแหน่งไหนมากหรือน้อย
แต่ในความเป็นจริงแล้วระบบการคิดของมนุษย์เราไม่ควรจะง่ายๆแค่นั้น เช่นว่าเลข 0 บางครั้งอาจถูกเขียนเบี้ยวมาอยู่ทางขวามากหน่อย จนเส้นไปพาดผ่านตรงกลาง พอมีกรณีแบบนี้ขึ้นโอกาสทายผิดก็มีสูง
ปกติควรพิจารณาว่าเลข 0 เป็นสิ่งที่มีขอบและรูตรงกลาง ตรงไหนอาจจะเป็นขอบหรือรูก็ไม่รู้ แม้รูจะมักอยู่ตรงกลางสุด แต่ก็ไม่เสมอไป
ดังนั้นจำเป็นต้องสามารถคิดในลักษณะที่ว่า "ถ้าตรงนี้มีการเขียนแล้วตรงนั้นต้องไม่มีถึงจะควรเป็นเลขนี้ แต่ถ้าตรงนี้ไม่มีก็ควรต้องมีตรงนี้"
ซึ่งระบบที่เขียนขึ้นข้างต้นนี้จะยังไม่สามารถพิจารณาอะไรซับซ้อนหลายตลบแบบนั้นได้เพราะมีแค่ชั้นเดียว
อีกทั้งข้อมูลของทั้ง 784 ช่องถูกป้อนในลักษณะที่เป็นมิติเดียว แถมไม่มีอะไรเป็นตัวบอกว่าช่องไหนอยู่ติดกัน ช่องที่ 1,2,3 ก็เป็นตัวแปรต้นต้นตัวนึงเหมือนๆกัน ไม่ได้ถูกพิจารณาว่าช่อง 2 กับช่อง 1 มีความใกล้ชิดกันมากกว่าช่อง 3 กับช่อง 1
เพื่อที่จะให้เครื่องเรียนรู้อะไรซับซ้อนขึ้น จึงจำเป็นต้องสร้างระบบการเรียนรู้ที่ซับซ้อนขึ้น
วิธีการหนึ่งที่นิยมใช้กันมากก็คือ การเอาส่วนคำนวณการถดถอยโลจิสติกมาซ้อนต่อกันเป็น ๒ ชั้นขึ้นไป ซึ่งก็คือการสร้างเครือข่ายประสาทเทียม (神经网路, neural network)
นี่ก็เป็นเรื่องที่ตั้งใจจะเขียนถึงในบทความต่อๆไป
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib