การทำต้นไม้ตัดสินใจโดยใช้ sklearn
เขียนเมื่อ 2017/11/08 10:45
แก้ไขล่าสุด 2021/09/28 16:42
บทความที่แล้วได้แนะนำวิธีการทำต้นไม้ตัดสินใจไปแล้ว https://phyblas.hinaboshi.com/20171105
จากนั้นก็ได้ทิ้งท้ายเอาไว้ว่าเราสามารถทำต้นไม้ตัดสินใจได้อย่างง่ายดายกว่าโดยใช้ sklearn ดังนั้นในตอนนี้จะลองมาใช้กันดู
วิธีการใช้จะคล้ายกับการถดถอยโลจิสติก (https://phyblas.hinaboshi.com/20171010) และเพื่อนบ้านใกล้ที่สุด k ตัว (https://phyblas.hinaboshi.com/20171031) ที่ได้แนะนำไปก่อนหน้า
นั่นคือเริ่มจากสร้างออบเจ็กต์ขึ้นมา แล้วก็ใช้ fit เพื่อเรียนรู้ จากนั้นก็ใช้ prefict เพื่อทำนาย
ตัวอย่างการใช้ sklearn
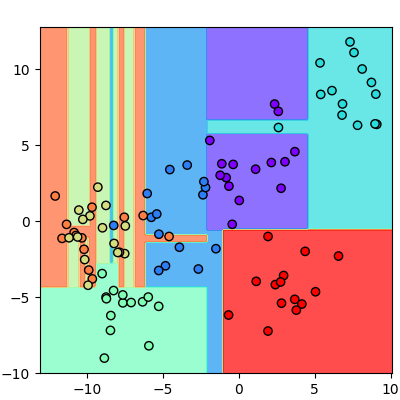
หากลองดูรายละเอียดภายในออบเจ็กต์ของต้นไม้ตัดสินใจจะพบว่ามีไฮเพอร์พารามิเตอร์มากมายที่สามารถปรับได้
ได้
รายละเอียดภายในค่อนข้างซับซ้อนจึงจะยังไม่พูดถึงตรงนี้ แต่ที่สำคัญที่สุดก็คือ max_depth
ถ้าหากเราไม่ใส่ค่านี้จะเป็นการให้แตกกิ่งไปเรื่อยๆจนกว่าจะแบ่งแยกข้อมูลได้ถูกต้องทั้งหมด
แต่ถ้าระบุ max_depth ลงไปก็จะเป็นการจำกัดจำนวนครั้งในการแตก
ลองนำข้อมูลตัวอย่างเดิมมาแบ่งแบบเดิมแต่คราวนี้กำหนดความลึกให้เปลี่ยนไปเรื่อยๆแล้วเทียบกันดู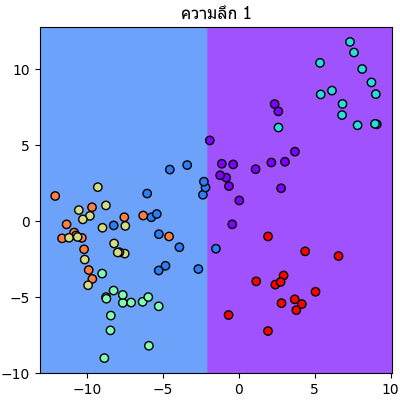
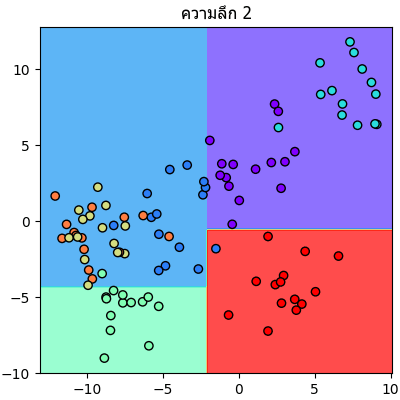
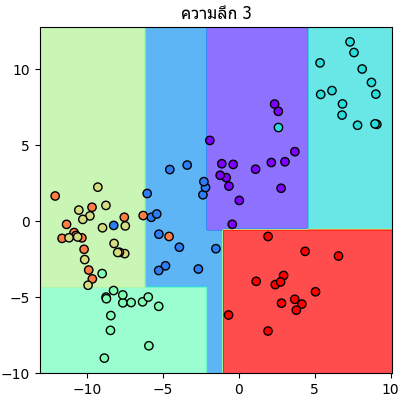
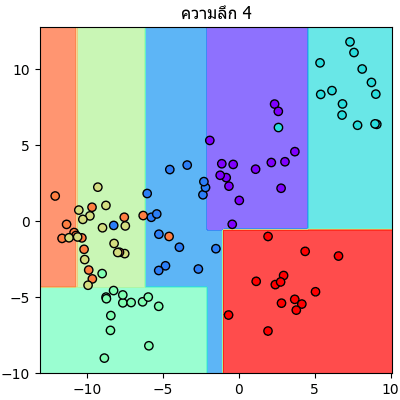
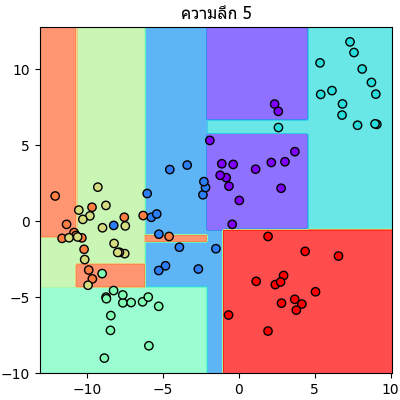
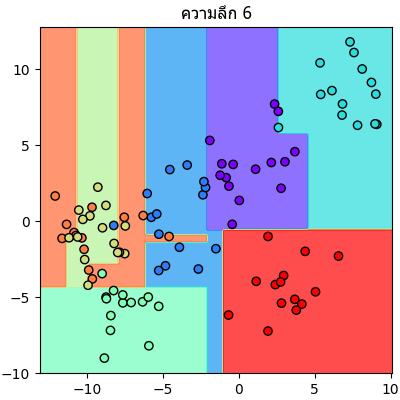
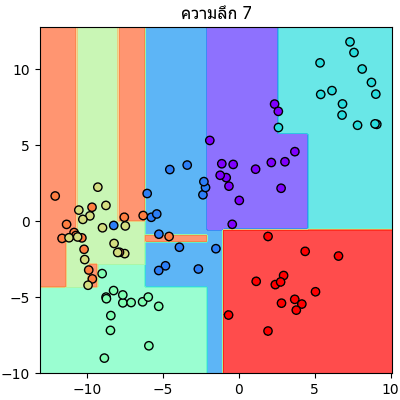
จะเห็นลำดับการแบ่งไปเรื่อยๆทีละขั้นชัดเจน
ส่วน criterion คือวิธีการคำนวณค่าความไม่บริสุทธิ์ เลือกได้ระหว่าง gini กับ entropy
ค่าตั้งต้นคือ gini หากลองเปลี่ยนเป็น entropy ดูก็อาจได้ผลต่างไปจากเดิม แต่ก็จะไม่ต่างกันมาก
นอกจากนี้ก็ยังมีอีกมากมายให้ปรับได้ ดูรายละเอียดต่อได้ใน http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html
สิ่งที่น่าจะใช้ประโยชน์ได้อย่างดีอีกอย่างสำหรับต้นไม้ตัดสินใจก็คือ สามารถวิเคราะห์ความสำคัญของตัวแปรได้
สามารถทำได้โดยดูที่ค่าแอตทริบิวต์ .feature_importances_ หลังจากที่ได้ทำการ fit ไปเสร็จแล้ว
ลองยกตัวอย่าง เช่น ลองสร้างกลุ่มก้อนที่มีตัวแปรที่พิจารณาอยู่ ๖ ตัว แล้วให้ใช้ต้นไม้ตัดสินใจช่วยจำแนกดังนี้
จะเห็นว่าได้ค่าความสำคัญออกมา ซึ่งบอกให้รู้ว่าตัวแปรลำดับที่เท่าไหร่มีส่วนร่วมในการแบ่งแค่ไหน ค่ายิ่งมากยิ่งสำคัญ ทั้งหมดรวมกันจะเป็น 1
ซึ่งหากเราลองวาดภาพแสดงการกระจายค่าของตัวแปรที่สำคัญดูแบบนี้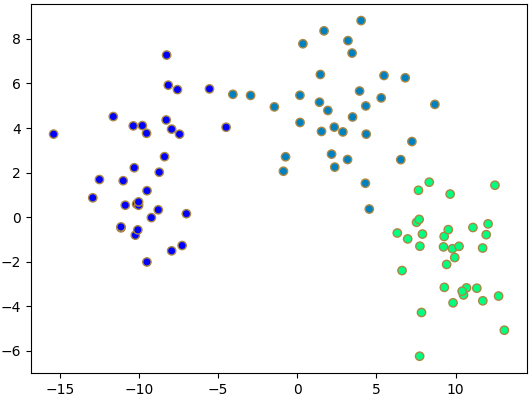
จะเห็นได้ว่าข้อมูลถูกแบ่งกันเป็นกลุ่มอย่างชัดเจน แสดงให้เห็นว่าสามารถใช้ตัวแปรทั้งสองตัวนี้อธิบายแบ่งแยกกลุ่มได้อย่างดี
แต่ถ้าเอาตัวแปรที่สำคัญน้อยสุดไปวาด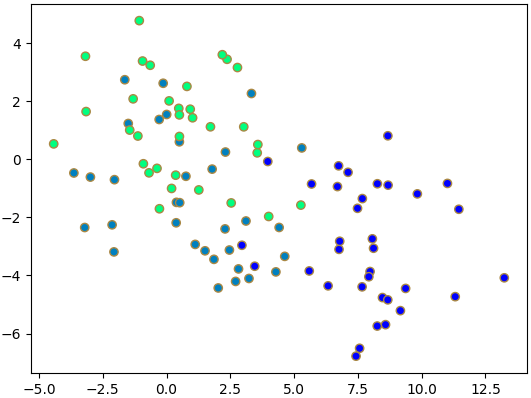
จะพบว่าข้อมูลมีการซ้อนทับ แสดงให้เห็นว่าตัวแปรสองตัวนี้ใช้อธิบายการจำแนกข้อมูลไม่ค่อยได้
จากนั้นก็ได้ทิ้งท้ายเอาไว้ว่าเราสามารถทำต้นไม้ตัดสินใจได้อย่างง่ายดายกว่าโดยใช้ sklearn ดังนั้นในตอนนี้จะลองมาใช้กันดู
วิธีการใช้จะคล้ายกับการถดถอยโลจิสติก (https://phyblas.hinaboshi.com/20171010) และเพื่อนบ้านใกล้ที่สุด k ตัว (https://phyblas.hinaboshi.com/20171031) ที่ได้แนะนำไปก่อนหน้า
นั่นคือเริ่มจากสร้างออบเจ็กต์ขึ้นมา แล้วก็ใช้ fit เพื่อเรียนรู้ จากนั้นก็ใช้ prefict เพื่อทำนาย
ตัวอย่างการใช้ sklearn
from sklearn.tree import DecisionTreeClassifier as Ditri
X,z = datasets.make_blobs(n_samples=100,n_features=2,centers=7,cluster_std=1.8,random_state=3)
dt = Ditri()
dt.fit(X,z)
nmesh = 200
mx,my = np.meshgrid(np.linspace(X[:,0].min()-1,X[:,0].max()+1,nmesh),np.linspace(X[:,1].min()-1,X[:,1].max()+1,nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = dt.predict(mX).reshape(nmesh,nmesh)
plt.figure(figsize=[4,4])
plt.axes([0.1,0.06,0.88,0.88],aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='rainbow',vmin=0,vmax=6)
plt.contourf(mx,my,mz,alpha=0.7,cmap='rainbow',zorder=0,vmin=0,vmax=6)
plt.show()
หากลองดูรายละเอียดภายในออบเจ็กต์ของต้นไม้ตัดสินใจจะพบว่ามีไฮเพอร์พารามิเตอร์มากมายที่สามารถปรับได้
print(dt)ได้
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False, random_state=None,
splitter='best')รายละเอียดภายในค่อนข้างซับซ้อนจึงจะยังไม่พูดถึงตรงนี้ แต่ที่สำคัญที่สุดก็คือ max_depth
ถ้าหากเราไม่ใส่ค่านี้จะเป็นการให้แตกกิ่งไปเรื่อยๆจนกว่าจะแบ่งแยกข้อมูลได้ถูกต้องทั้งหมด
แต่ถ้าระบุ max_depth ลงไปก็จะเป็นการจำกัดจำนวนครั้งในการแตก
ลองนำข้อมูลตัวอย่างเดิมมาแบ่งแบบเดิมแต่คราวนี้กำหนดความลึกให้เปลี่ยนไปเรื่อยๆแล้วเทียบกันดู
for i in range(1,8):
dt = Ditri(max_depth=i)
dt.fit(X,z)
nmesh = 200
mx,my = np.meshgrid(np.linspace(X[:,0].min()-1,X[:,0].max()+1,nmesh),np.linspace(X[:,1].min()-1,X[:,1].max()+1,nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = dt.predict(mX).reshape(nmesh,nmesh)
plt.figure(figsize=[4,4])
plt.axes([0.1,0.06,0.88,0.88],aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='rainbow',vmin=0,vmax=6)
plt.contourf(mx,my,mz,alpha=0.7,cmap='rainbow',zorder=0,vmin=0,vmax=6)
plt.title(u'ความลึก %d'%i,family='Tahoma')
plt.savefig('dt%02d.png'%i)
plt.close()






จะเห็นลำดับการแบ่งไปเรื่อยๆทีละขั้นชัดเจน
ส่วน criterion คือวิธีการคำนวณค่าความไม่บริสุทธิ์ เลือกได้ระหว่าง gini กับ entropy
ค่าตั้งต้นคือ gini หากลองเปลี่ยนเป็น entropy ดูก็อาจได้ผลต่างไปจากเดิม แต่ก็จะไม่ต่างกันมาก
นอกจากนี้ก็ยังมีอีกมากมายให้ปรับได้ ดูรายละเอียดต่อได้ใน http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html
สิ่งที่น่าจะใช้ประโยชน์ได้อย่างดีอีกอย่างสำหรับต้นไม้ตัดสินใจก็คือ สามารถวิเคราะห์ความสำคัญของตัวแปรได้
สามารถทำได้โดยดูที่ค่าแอตทริบิวต์ .feature_importances_ หลังจากที่ได้ทำการ fit ไปเสร็จแล้ว
ลองยกตัวอย่าง เช่น ลองสร้างกลุ่มก้อนที่มีตัวแปรที่พิจารณาอยู่ ๖ ตัว แล้วให้ใช้ต้นไม้ตัดสินใจช่วยจำแนกดังนี้
np.random.seed(6)
X,z = datasets.make_blobs(n_samples=100,n_features=6,centers=3,cluster_std=2.2)
dt = Ditri()
dt.fit(X,z)
fi = dt.feature_importances_
print(fi) # ได้ [ 0. 0. 0. 0.5049505 0.05657709 0.43847242]จะเห็นว่าได้ค่าความสำคัญออกมา ซึ่งบอกให้รู้ว่าตัวแปรลำดับที่เท่าไหร่มีส่วนร่วมในการแบ่งแค่ไหน ค่ายิ่งมากยิ่งสำคัญ ทั้งหมดรวมกันจะเป็น 1
ซึ่งหากเราลองวาดภาพแสดงการกระจายค่าของตัวแปรที่สำคัญดูแบบนี้
ia = fi.argsort()
plt.scatter(X[:,ia[-1]],X[:,ia[-2]],c=z,edgecolor='#aa8844',cmap='winter')
plt.show()
จะเห็นได้ว่าข้อมูลถูกแบ่งกันเป็นกลุ่มอย่างชัดเจน แสดงให้เห็นว่าสามารถใช้ตัวแปรทั้งสองตัวนี้อธิบายแบ่งแยกกลุ่มได้อย่างดี
แต่ถ้าเอาตัวแปรที่สำคัญน้อยสุดไปวาด
plt.scatter(X[:,ia[0]],X[:,ia[1]],c=z,edgecolor='#aa8844',cmap='winter')
plt.show()
จะพบว่าข้อมูลมีการซ้อนทับ แสดงให้เห็นว่าตัวแปรสองตัวนี้ใช้อธิบายการจำแนกข้อมูลไม่ค่อยได้
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn