การวิเคราะห์การจำแนกประเภทเชิงเส้น (LDA)
เขียนเมื่อ 2018/08/02 00:23
แก้ไขล่าสุด 2022/07/19 05:17
ก่อนหน้านี้ได้อธิบายถึงการวิเคราะห์องค์ประกอบหลัก (PCA) ไปแล้ว https://phyblas.hinaboshi.com/20180727
การวิเคราะห์องค์ประกอบหลักนั้นเป็นการวิเคราะห์แปลงระบบพิกัดใหม่โดยพิจารณาที่การกระจายตัวของข้อมูล โดยไม่ได้สนว่าข้อมูลแต่ละตัวนั้นถูกจัดอยู่ในกลุ่มไหน
แต่ว่าการกระจายตัวของข้อมูลไปในทางไหนมากก็ไม่ได้หมายถึงว่าการแบ่งกลุ่มจะกระจายตามแนวนั้นมากไปด้วยเสมอไป
ตัวอย่างเช่นข้อมูลที่หน้าตาดูคล้ายขนมปังฝรั่งเศสนี้
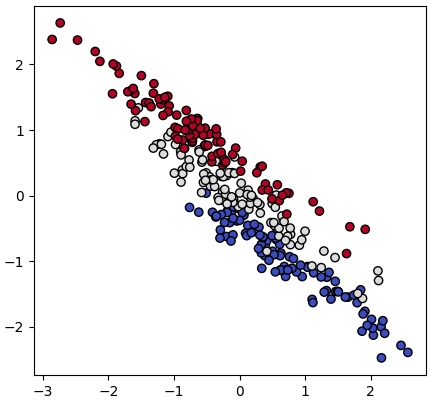
ข้อมูลดูจะกระจายตามแนวเฉียงบนซ้ายขวาล่างมาก แต่การแบ่งกลุ่มของข้อมูลไม่ได้กระจายไปตามแกนนั้นเลย
กรณีที่ต้องการวิเคราะห์เปลี่ยนแกนโดยพิจารณาแยกการกระจายของแต่ละกลุ่มไปด้วยนั้นจะนิยมใช้อีกวิธีหนึ่ง คือ การวิเคราะห์การจำแนกประเภทเชิงเส้น (线性判别分析, linear discriminant analysis) เรียกย่อๆว่า LDA
วิธีการนี้ถูกพัฒนาขึ้นตั้งแต่ปี 1936 โดยรอนัลด์ ฟิชเชอร์ (Ronald Fisher) นักสถิติ
ภาพตัวอย่างแสดงความแตกต่างระหว่างการวิเคราะห์องค์ประกอบหลัก (PCA) และ การวิเคราะห์การจำแนกประเภทเชิงเส้น (LDA)
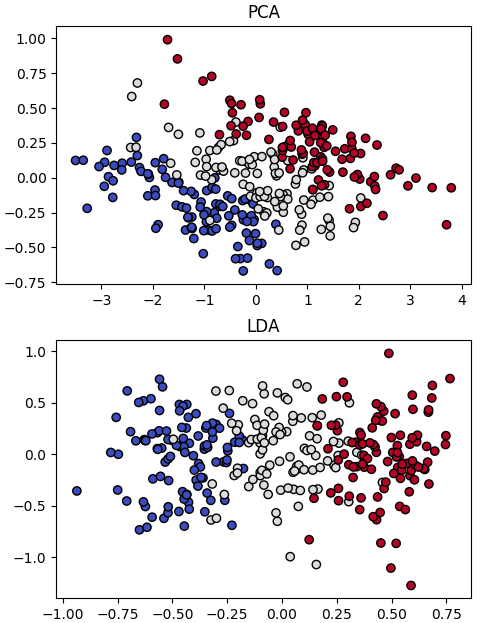
จะเห็นว่าการวิเคราะห์การจำแนกประเภทเชิงเส้นได้ทำให้ข้อมูลกระจายตัวแบ่งอยู่ในแกนนอน ในขณะที่การวิเคราะห์องค์ประกอบเฉพาะไม่ได้ทำแบบนี้
ในการวิเคราะห์การจำแนกประเภทเชิงเส้นนั้น สิ่งที่พิจารณาเป็นสำคัญคือ การให้ข้อมูลต่างกลุ่มกันกระจายอยู่ห่างกันที่สุด
ในขณะที่การวิเคราะห์องค์ประกอบหลักเป็นเทคนิคการเรียนรู้ของเครื่องแบบไม่มีผู้สอน กล่าวคือป้อนแค่ข้อมูลตัวแปรต้นที่ต้องการวิเคราะห์เข้าไป การวิเคราะห์การจำแนกประเภทเชิงเส้นเป็นเทคนิคการเรียนรู้แบบมีผู้สอน กล่าวคือต้องป้อนทั้งข้อมูลตัวแปรต้นและตัวแปรตามเพื่อใช้วิเคราะห์ ดังนั้นจึงมีประสิทธิภาพในการวิเคราะห์ข้อมูลมากกว่า
ขั้นตอนการทำการวิเคราะห์การจำแนกประเภทเชิงเส้น
1. ทำข้อมูลให้เป็นมาตรฐาน
2. หาค่าเฉลี่ยของข้อมูลแต่ละกลุ่ม
3. คำนวณเมทริกซ์ความแปรปรวนร่วมเกี่ยวของข้อมูลภายในแต่ละกลุ่มแล้วนำมารวมกัน (SW)
4. คำนวณเมทริกซ์ความแปรปรวนร่วมเกี่ยวของของข้อมูลระหว่างต่างกลุ่มแล้วคูณจำนวนข้อมูลในกลุ่มแล้วรวมกัน (SB)
5. คำนวณ SW-1SB
6. หาเวกเตอร์ลักษณะเฉพาะและค่าลักษณะเฉพาะของ SW-1SB
7. คัดเลือกเวกเตอร์ลักษณะเฉพาะที่มีค่าลักษณะเฉพาะมากที่สุดกี่อันดับแรกตามที่ต้องการ นำมาใช้เป็นตัวคูณสำหรับแปลงพิกัด
ผลรวมเมทริกซ์ความแปรปรวนร่วมเกี่ยวของแต่ละกลุ่ม SW คำนวนโดย
..(1)
โดย Di คือเซตของกลุ่มที่ i มีกลุ่มอยู่ c กลุ่ม
cov หมายถึงเมทริกซ์ความแปรปรวนร่วมเกี่ยว
SB คำนวณโดย
..(2)
ni คือจำนวนข้อมูลในกลุ่ม i
mi คือค่าเฉลี่ยของค่าในกลุ่ม i
m คือค่าเฉลี่ยของข้อมูลทั้งหมด ในที่นี้ถ้าได้ทำการปรับข่้อมูลให้เป็นมาตรฐานในขั้นตอนแรกไปแล้วค่าควรจะเป็น 0
เมื่อได้ SW กับ SB แล้วที่เหลือก็เหมือนกับการวิเคราะห์องค์ประกอบหลัก คือไปหาเวกเตอร์ลักษณะเฉพาะ
ตัวอย่างการเขียนโค้ด
พิจารณาข้อมูลหน้าตาแบบนี้
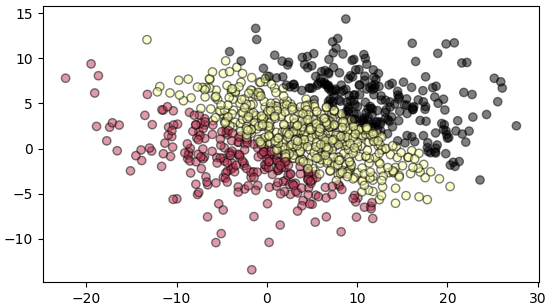
นำมาทำการวิเคราะห์การจำแนกประเภทเชิงเส้น
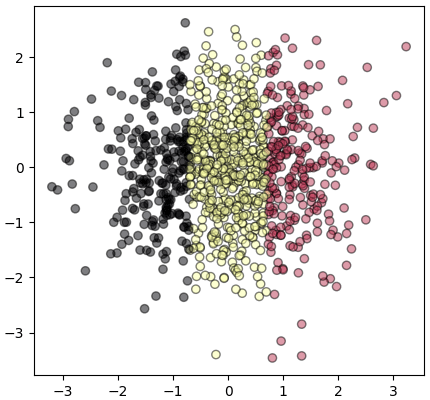
ข้อมูลกระจายแบ่งกลุ่มตามแนวนอนได้ตามที่ต้องการ
ต่อมาลองเรียบเรียงนำมาเขียนเป็นคลาสให้เรียบร้อยแบบนี้
ภายในคลาสได้รวมส่วนที่ทำข้อมูลให้เป็นมาตรฐานไว้ด้วยแล้ว แต่ตั้งไว้ให้สามารถเลือกได้ว่าจะทำหรือเปล่า
ลองนำมาใช้
หลังแปลง
ใช้ sklearn
คลาสสำหรับการวิเคราะห์การจำแนกประเภทเชิงเส้นได้ถูกบรรจุอยู่ใน sklearn อยู่แล้ว สามารถหยิบมาใช้ได้เลย สะดวกดีมาก
ตัวอย่าง สร้างข้อมูลกลุ่มก้อนที่มี ๑๐ มิติ แล้วหาทางแสดงให้อยู่ในสองมิติ
ในที่นี้ n_components เป็นตัวกำหนดว่าจะให้ข้อมูลเหลือกี่มิติ ถ้าไม่กำหนดไปจะได้ข้อมูลกลับมาเป็นมิติจำนวนเท่าเดิม
อ้างอิง
การวิเคราะห์องค์ประกอบหลักนั้นเป็นการวิเคราะห์แปลงระบบพิกัดใหม่โดยพิจารณาที่การกระจายตัวของข้อมูล โดยไม่ได้สนว่าข้อมูลแต่ละตัวนั้นถูกจัดอยู่ในกลุ่มไหน
แต่ว่าการกระจายตัวของข้อมูลไปในทางไหนมากก็ไม่ได้หมายถึงว่าการแบ่งกลุ่มจะกระจายตามแนวนั้นมากไปด้วยเสมอไป
ตัวอย่างเช่นข้อมูลที่หน้าตาดูคล้ายขนมปังฝรั่งเศสนี้

ข้อมูลดูจะกระจายตามแนวเฉียงบนซ้ายขวาล่างมาก แต่การแบ่งกลุ่มของข้อมูลไม่ได้กระจายไปตามแกนนั้นเลย
กรณีที่ต้องการวิเคราะห์เปลี่ยนแกนโดยพิจารณาแยกการกระจายของแต่ละกลุ่มไปด้วยนั้นจะนิยมใช้อีกวิธีหนึ่ง คือ การวิเคราะห์การจำแนกประเภทเชิงเส้น (线性判别分析, linear discriminant analysis) เรียกย่อๆว่า LDA
วิธีการนี้ถูกพัฒนาขึ้นตั้งแต่ปี 1936 โดยรอนัลด์ ฟิชเชอร์ (Ronald Fisher) นักสถิติ
ภาพตัวอย่างแสดงความแตกต่างระหว่างการวิเคราะห์องค์ประกอบหลัก (PCA) และ การวิเคราะห์การจำแนกประเภทเชิงเส้น (LDA)

จะเห็นว่าการวิเคราะห์การจำแนกประเภทเชิงเส้นได้ทำให้ข้อมูลกระจายตัวแบ่งอยู่ในแกนนอน ในขณะที่การวิเคราะห์องค์ประกอบเฉพาะไม่ได้ทำแบบนี้
ในการวิเคราะห์การจำแนกประเภทเชิงเส้นนั้น สิ่งที่พิจารณาเป็นสำคัญคือ การให้ข้อมูลต่างกลุ่มกันกระจายอยู่ห่างกันที่สุด
ในขณะที่การวิเคราะห์องค์ประกอบหลักเป็นเทคนิคการเรียนรู้ของเครื่องแบบไม่มีผู้สอน กล่าวคือป้อนแค่ข้อมูลตัวแปรต้นที่ต้องการวิเคราะห์เข้าไป การวิเคราะห์การจำแนกประเภทเชิงเส้นเป็นเทคนิคการเรียนรู้แบบมีผู้สอน กล่าวคือต้องป้อนทั้งข้อมูลตัวแปรต้นและตัวแปรตามเพื่อใช้วิเคราะห์ ดังนั้นจึงมีประสิทธิภาพในการวิเคราะห์ข้อมูลมากกว่า
ขั้นตอนการทำการวิเคราะห์การจำแนกประเภทเชิงเส้น
1. ทำข้อมูลให้เป็นมาตรฐาน
2. หาค่าเฉลี่ยของข้อมูลแต่ละกลุ่ม
3. คำนวณเมทริกซ์ความแปรปรวนร่วมเกี่ยวของข้อมูลภายในแต่ละกลุ่มแล้วนำมารวมกัน (SW)
4. คำนวณเมทริกซ์ความแปรปรวนร่วมเกี่ยวของของข้อมูลระหว่างต่างกลุ่มแล้วคูณจำนวนข้อมูลในกลุ่มแล้วรวมกัน (SB)
5. คำนวณ SW-1SB
6. หาเวกเตอร์ลักษณะเฉพาะและค่าลักษณะเฉพาะของ SW-1SB
7. คัดเลือกเวกเตอร์ลักษณะเฉพาะที่มีค่าลักษณะเฉพาะมากที่สุดกี่อันดับแรกตามที่ต้องการ นำมาใช้เป็นตัวคูณสำหรับแปลงพิกัด
ผลรวมเมทริกซ์ความแปรปรวนร่วมเกี่ยวของแต่ละกลุ่ม SW คำนวนโดย
..(1)
โดย Di คือเซตของกลุ่มที่ i มีกลุ่มอยู่ c กลุ่ม
cov หมายถึงเมทริกซ์ความแปรปรวนร่วมเกี่ยว
SB คำนวณโดย
..(2)
ni คือจำนวนข้อมูลในกลุ่ม i
mi คือค่าเฉลี่ยของค่าในกลุ่ม i
m คือค่าเฉลี่ยของข้อมูลทั้งหมด ในที่นี้ถ้าได้ทำการปรับข่้อมูลให้เป็นมาตรฐานในขั้นตอนแรกไปแล้วค่าควรจะเป็น 0
เมื่อได้ SW กับ SB แล้วที่เหลือก็เหมือนกับการวิเคราะห์องค์ประกอบหลัก คือไปหาเวกเตอร์ลักษณะเฉพาะ
ตัวอย่างการเขียนโค้ด
พิจารณาข้อมูลหน้าตาแบบนี้
import numpy as np
import matplotlib.pyplot as plt
X = np.random.normal(2,4,[1000,2])
z = ((X[:,0]+X[:,1])<8)*2-((X[:,0]+X[:,1])<0)
X[:,0] *= 2
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='inferno',alpha=0.5)
plt.show()
นำมาทำการวิเคราะห์การจำแนกประเภทเชิงเส้น
from sklearn.preprocessing import StandardScaler as StaSke
X = StaSke().fit_transform(X) # ทำให้เป็นมาตรฐาน
praeruam_naiklum = [] # ความแปรปรวนร่วมเกี่ยวภายในแต่ละกลุ่ม
praeruam_rawangklum = [] # ความแปรปรวนร่วมเกี่ยวระหว่างกลุ่ม
for i in range(max(z)+1):
X_i = X[z==i] # ข้อมุลในแต่ละกลุ่ม
n_naiklum = X_i.shape[0] # จำนวนข้อมุลในแต่ละกลุ่ม
chalia_naiklum = X_i.mean(0) # ค่าเฉลี่ยภายในกลุ่ม
praeruam_naiklum.append(np.cov(X_i.T))
praeruam_rawangklum.append(n_naiklum*chalia_naiklum[:,None]*chalia_naiklum)
SW = np.sum(praeruam_naiklum,0)
SB = np.sum(praeruam_rawangklum,0)
praeruam = np.linalg.inv(SW).dot(SB)
kha_eig,vec_eig = np.linalg.eigh(praeruam) # หาเวกเตอร์และค่าลักษณะเฉพาะ
Xi = X.dot(vec_eig[:,::-1]) # คำนวณค่าในพิกัดใหม่
plt.axes(aspect=1)
plt.scatter(Xi[:,0],Xi[:,1],c=z,edgecolor='k',cmap='inferno',alpha=0.5)
plt.show()
ข้อมูลกระจายแบ่งกลุ่มตามแนวนอนได้ตามที่ต้องการ
ต่อมาลองเรียบเรียงนำมาเขียนเป็นคลาสให้เรียบร้อยแบบนี้
class WikhroKanchamnaekPraphetChoengsen:
def rianru(self,X,z,sta=1):
if(sta):
self.staske = StaSke()
X = self.staske.fit_transform(X)
SW,SB = [],[]
for i in range(max(z)+1):
X_i = X[z==i]
m_i = X_i.mean(0)
SW.append(np.cov(X_i.T))
SB.append(X_i.shape[0]*m_i[:,None]*m_i)
SW = np.sum(SW,0)
SB = np.sum(SB,0)
kha_eig,vec_eig = np.linalg.eigh(np.linalg.inv(SW).dot(SB))
self.V = vec_eig[:,::-1]
self.a = kha_eig[::-1]/kha_eig.sum()
def plaeng(self,X,sta=1):
if(sta):
X = self.staske.transform(X)
return X.dot(self.V)
def rianru_plaeng(self,X,z,sta=1):
if(sta):
self.staske = StaSke()
X = self.staske.fit_transform(X)
self.rianru(X,z,sta=0)
return self.plaeng(X,sta=0)ภายในคลาสได้รวมส่วนที่ทำข้อมูลให้เป็นมาตรฐานไว้ด้วยแล้ว แต่ตั้งไว้ให้สามารถเลือกได้ว่าจะทำหรือเปล่า
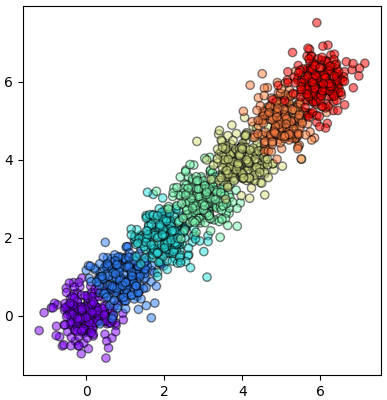
ลองนำมาใช้
X = (np.random.normal(0,0.4,[200,2,7]) + np.arange(7)).T.reshape(1400,2)
z = np.tile(np.arange(7),[200,1]).T.ravel()
plt.axes(aspect=1) # ระบบพิกัดเก่า
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='rainbow',alpha=0.5)
Xi = WikhroKanchamnaekPraphetChoengsen().rianru_plaeng(X,z) # แปลงพิกัด
plt.figure()
plt.axes(aspect=1) # ระบบพิกัดใหม่
plt.scatter(Xi[:,0],Xi[:,1],c=z,edgecolor='k',cmap='rainbow',alpha=0.5)
plt.show()
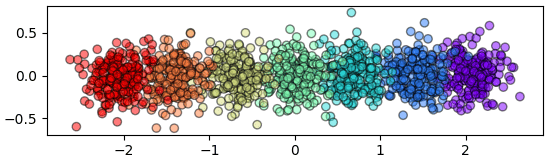
หลังแปลง

ใช้ sklearn
คลาสสำหรับการวิเคราะห์การจำแนกประเภทเชิงเส้นได้ถูกบรรจุอยู่ใน sklearn อยู่แล้ว สามารถหยิบมาใช้ได้เลย สะดวกดีมาก
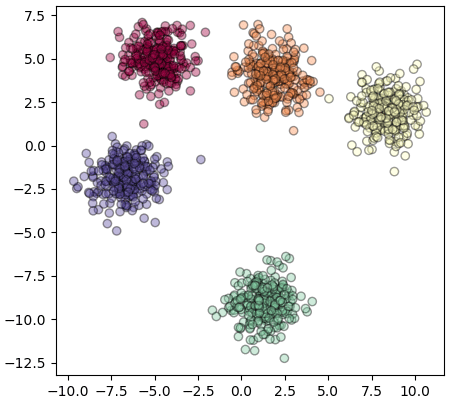
ตัวอย่าง สร้างข้อมูลกลุ่มก้อนที่มี ๑๐ มิติ แล้วหาทางแสดงให้อยู่ในสองมิติ
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn import datasets
X,z = datasets.make_blobs(1250,n_features=10,centers=5,cluster_std=2,random_state=5)
lda = LDA(n_components=2)
Xi = lda.fit_transform(X,z)
plt.axes(aspect=1)
plt.scatter(Xi[:,0],Xi[:,1],c=z,edgecolor='k',cmap='Spectral',alpha=0.4)
plt.show()
ในที่นี้ n_components เป็นตัวกำหนดว่าจะให้ข้อมูลเหลือกี่มิติ ถ้าไม่กำหนดไปจะได้ข้อมูลกลับมาเป็นมิติจำนวนเท่าเดิม
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn