[python] การทำแผนที่โยงก่อร่างตัวเอง (SOM)
เขียนเมื่อ 2018/08/05 00:27
แก้ไขล่าสุด 2022/07/11 12:40
การทำแผนที่โยงก่อร่างตัวเอง (自组织映射, self-organizing maps) หรือนิยมเรียกย่อๆว่า SOM เป็นเทคนิคหนึ่งของการเรียนรู้ของเครื่องแบบไม่มีผู้สอน
แนวคิด
SOM เป็นเทคนิคในการวิเคราะห์โครงสร้างของการกระจายตัวของข้อมูลโดยอัตโนมัติ แล้ววาดออกมาเป็นแผนที่แสดงการจัดเรียงของข้อมูลนั้นในพิกัดของแผนที่ที่ถูกสร้างขึ้น
ตัวอย่างเช่นเรามีข้อมูลที่กระจายตัวในสองมิติอยู่ในลักษณะแบบนี้
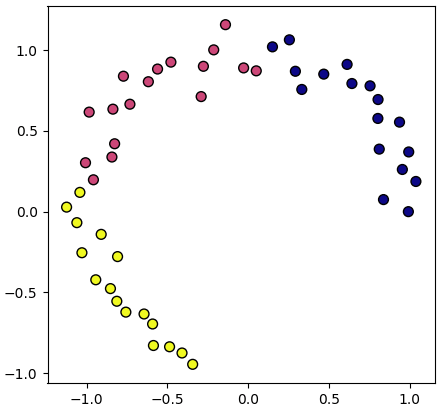
เราสามารถใช้ SOM หาโครงสร้างการกระจายของข้อมูลแล้วลากเส้นโค้งผ่านกลุ่มข้อมูลเหล่านั้น
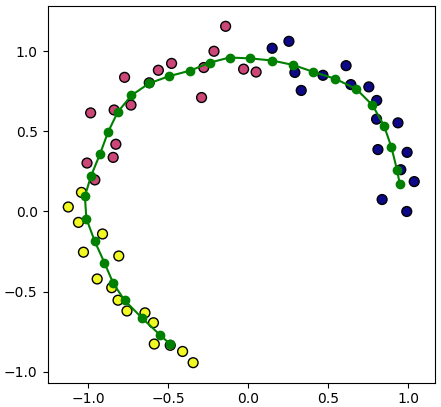
แล้วแสดงข้อมูลเหล่านั้นออกมาใหม่ในรูปหนึ่งมิติแบบนี้
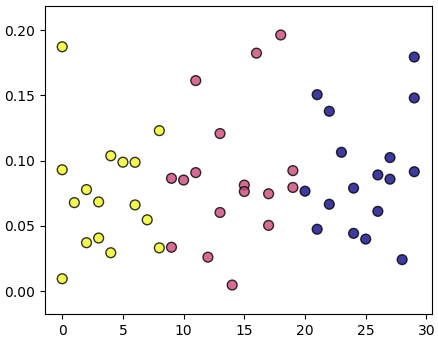
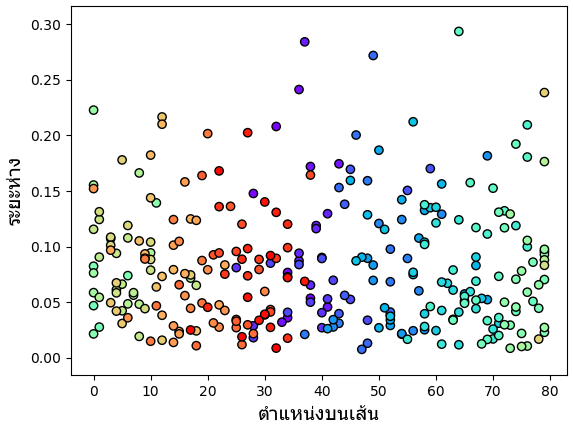
ในที่นี้แกนนอนแสดงดัชนีตำแหน่งบนเส้นโค้งที่ใกล้จุดนั้นๆมากที่สุด ส่วนแนวตั้งเป็นระยะห่างระหว่างจุดนั้นกับจุดบนเส้นที่ใกล้สุด
หรือเช่นข้อมูลที่กระจายในสามมิติแบบนี้
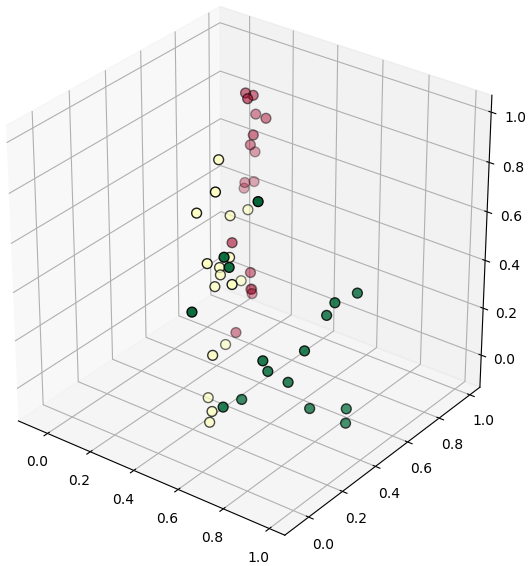
เราสามารถใช้ SOM เพื่อสร้างแผ่นผ้าสี่เหลี่ยมโค้งๆเป็นโครงข่ายแผ่พาดผ่านจุดเหล่านี้
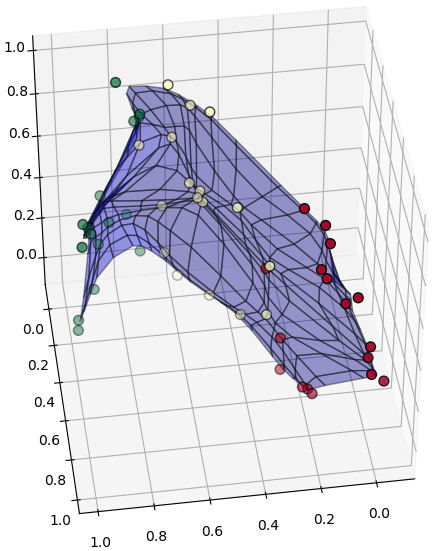
แล้วก็แสดงตำแหน่งจุดเหล่านี้ภายในพิกัดของโครงข่ายแผ่นผ้านั้น
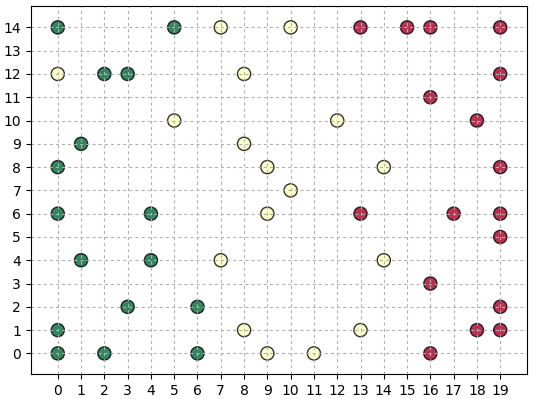
โครงสร้างทั้งหมดนี้ อัลกอริธึมของ SOM สามารถทำการหาให้เราได้โดยอัตโนมัติ
SOM มักถูกใช้กับข้อมูลที่มีจำนวนมิติมาก เพื่อทำแผนที่โครงสร้างของข้อมูลนั้นในมิติที่น้อยลง เป็นการลดมิติของข้อมูล และเป็นการทำให้มองเห็นภาพง่ายขึ้น โดยทั่วไปแล้ว SOM นิยมทำเป็นแผ่นสองมิติ ซึ่งมองแล้วก็จะเหมือนเอาข้อมูลทั้งหมดมาจับวางลงบนกระดาษกลายเป็นเหมือนแผ่นแผนที่ให้เห็นว่ากระจายตัวกันยังไง
เทคนิคนี้คิดค้นในปี 1981 โดย เต็วโวะ โกะโฮะเน็น (Teuvo Kohonen) ชาวฟินแลนด์ บางครั้งจึงถูกเรียกว่า แผนที่โกะโฮะเน็น (Kohonen map)
เทคนิคนี้จัดว่าเป็นโครงข่ายประสาทเทียม (人工神经网络, artificial neural network) ชนิดหนึ่ง เพียงแต่ว่าแนวคิดแตกต่างจากโครงข่ายประสาทเทียมซึ่งคนทั่วไปคุ้นเคยซึ่งมีพื้นฐานมาจากเพอร์เซ็ปตรอน
แนวคิด SOM มีพื้นฐานมาจากการเลียนแบบระบบการทำงานของสมองมนุษย์ เซลล์ประสาทในแต่ละส่วนของเปลือกสมองจะมีความไวต่อสิ่งเร้าในรูปแบบต่างๆไม่เท่ากัน แต่ว่าส่วนที่ใกล้กันจะมีแนวโน้มที่จะไวต่ออะไรที่ใกล้เคียงกัน
เส้นโค้งใน SOM 1 มิติ หรือแผ่นผ้าใน SOM 2 มิตินี้มักถูกเรียกว่าเป็นโครงข่ายประสาท โดยแต่ละจุดบนแผ่นหรือเส้นนั้นเรียกว่าเป็นเซลล์ประสาท (neuron)
เพื่อให้สั้นๆและเข้าใจตรงกัน ต่อจากตรงนี้ไปจะเรียกเส้นหรือแผ่นโครงข่ายนี้ว่า "โครงข่าย" เรียกจุดบนโครงข่ายว่า "เซลล์"
อัลกอริธึม
เป้าหมายของ SOM คือการสร้างเส้นโค้งหรือระนาบโค้งที่ลากผ่านใกล้จุดต่างๆได้โดยอัตโนมัติ
วิธีการก็คือ เริ่มแรกสุ่มตำแหน่งของเซลล์ของเส้นโครงข่ายขึ้นมาก่อนแบบสุ่ม จากนั้นก็ค่อยๆทำการปรับไปเรื่อยๆจนสุดท้ายเซลล์ของเส้นโครงข่ายไปวางตัวอยู่บนจุดของข้อมูล ดังภาพนี้

ขั้นตอนมีดังนี้
1. สร้างอาเรย์ตำแหน่งของจุดข้อมูล
..(1)
โดย n คือจำนวนจุดข้อมูล ส่วน m คือมิติของพิกัดข้อมูล
2. สร้างอาเรย์แสดงตำแหน่งภายในพิกัดข้อมูลเดิมของแต่ละเซลล์ของโครงข่าย
..(2)
โดย ν เป็นจำนวนเซลล์ในโครงข่าย
3. สร้างอาเรย์แสดงตำแหน่งเซลล์ภายในพิกัดโครงข่าย
ถ้าเครือข่ายมีมิติเดียวจะได้ว่า
..(3)
ถ้ามีสองมิติจะได้เป็น
..(4)
โดย ν0 คือจำนวนเซลล์ตามแกนตั้ง ν1 คือจำนวนเซลล์ตามแกนนอน ในที่นี้จำนวนเซลล์รวมทั้งหมดคือ ν = ν0×ν1
4. หยิบจุดข้อมูลจุดหนึ่งขึ้นมาพิจารณา คำนวณหาระยะทางแล้วดูว่าเซลล์ไหนบนโครงข่ายอยู่ใกล้จุดนั้นมากที่สุด
ระยะทางโดยทั่วไปแล้วคำนวณแบบยูคลิดธรรมดา คือรากที่สองของผลรวมกำลังสอง
..(5)
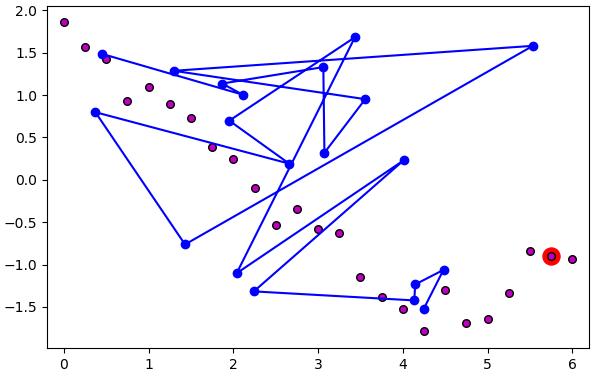
5. ย้ายเซลล์ที่อยู่ใกล้สุดบนโครงข่ายนั้นให้เข้าไปใกล้จุดที่พิจารณา โดยเซลล์ที่อยู่ใกล้ๆกันก็จะได้รับอิทธิพลทำให้เคลื่อนเข้าใกล้ไปด้วย ยิ่งเป็นเซลล์ที่อยู่ใกล้กันในพิกัดของโครงข่าย (ค่า c ใกล้กัน) ก็ยิ่งเคลื่อนตามไปมาก
การเปลี่ยนแปลงคำนวณตามนี้
..(6)
โดย f เป็นฟังก์ชันที่แสดงอัตราการเปลี่ยนแปลงโดยค่าจะขึ้นอยู่กับว่าห่างจากเซลล์ใกล้สุดเท่าไหร่ในพิกัดของโครงข่าย
ให้จินตนาการว่าเหมือนเราจับส่วนหนึ่งของเส้นด้ายให้เลื่อนไปบนพื้น ส่วนที่อยู่ใกล้ๆก็จะต้องเลื่อนตามไปด้วย แต่ส่วนไกลๆจะแทบไม่เลื่อนตาม
โดยทั่วไปจะใช้ฟังก์ชันที่ลดลงเรื่อยๆตามระยะห่าง เช่นฟังก์ชันเกาส์
..(7)
โดย c* เป็นตำแหน่งของเซลล์ใกล้สุด
โดย rt เป็นอัตราการลดอิทธิพลตามระยะทาง
ส่วน ηt เป็นอัตราการเรียนรู้
โดยทั่วไปทั้ง rt และ ηt จะไม่คงตัว แต่จะกำหนดให้ยิ่งเวลาผ่านไปก็ยิ่งลดลงไปเรื่อยๆ นั่นหมายถึงยิ่งเวลาผ่านไปการเปลี่ยนแปลงก็จะยิ่งน้อย
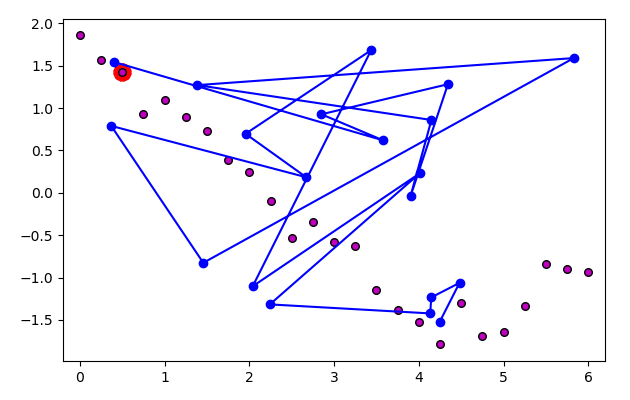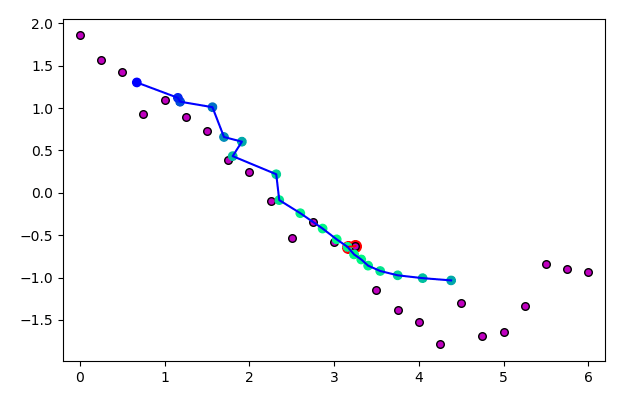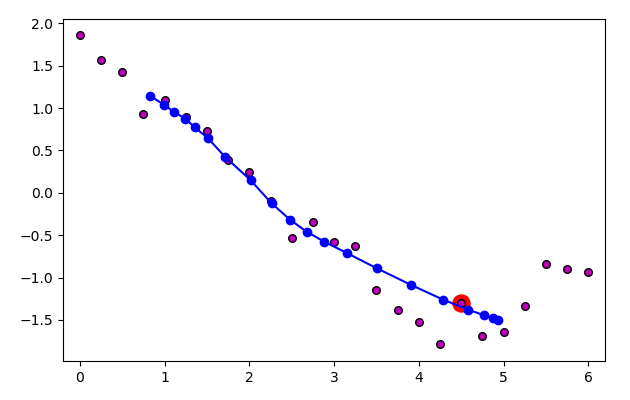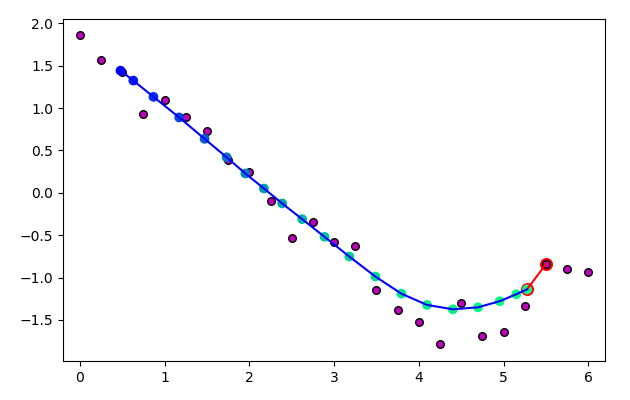
ภาพนี้แสดงจุดที่พิจารณาและเซลล์ใกล้สุดโดยล้อมด้วยกรอบแดงและเชื่อมด้วยเส้นแดง ส่วนสีของจุดเซลล์บนเส้นโครงข่ายแสดงระดับอิทธิพล ยิ่งอยู่ในลำดับใกล้กับเซลล์ใกล้สุดก็ยิ่งเป็นสีเขียว และจะมีการเลื่อนตำแหน่งมาก รูปล่างแสดงตำแหน่งหลังเลื่อนไปแล้ว
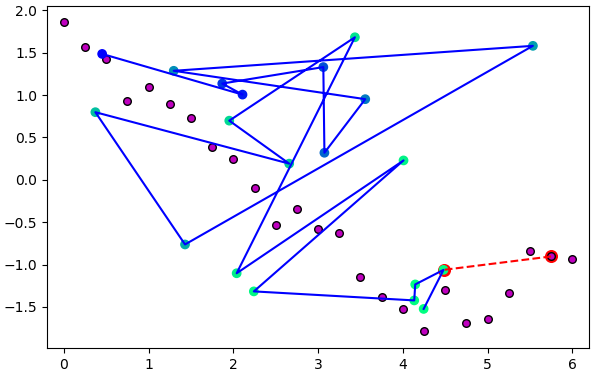
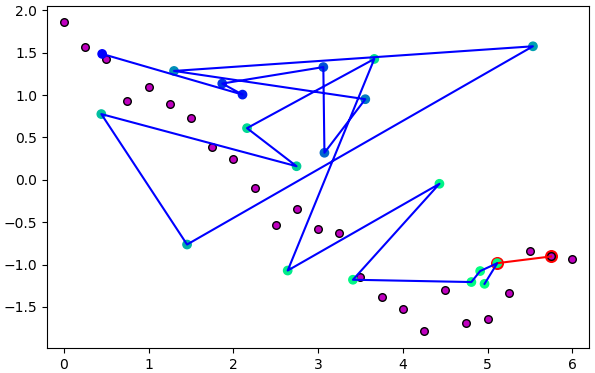
6. ทำซ้ำข้อ 4. ไปเรื่อยๆโดยเปลี่ยนจุดข้อมูลที่พิจารณา
7. พอใช้จุดข้อมูลครบทุกจุดก็วนกลับมาใช้จุดเดิมใหม่ โดยในรอบใหม่นี้อัตราการเรียนรู้จะลดลงเรื่อยๆในแต่ละรอบ แล้วก็ทำซ้ำใหม่ไปเรื่อยๆจนครบจำนวนครั้งที่ต้องการ
rt และ ηt อาจกำหนดให้ลดลงเรื่อยๆแบบเอกซ์โพเนนเชียล
..(8)
..(9)
τ เป็นอัตราการลดค่าตามเวลา
จากขั้นตอนทั้งหมดนี้จะเห็นว่ามีไฮเพอร์พารามิเตอร์ที่ต้องปรับอยู่ ๔ ตัวคือ
- ขนาดของโครงข่าย ν
- อัตราการเรียนรู้ตั้งต้น η
- r
- τ
นอกจากนี้ฟังก์ชัน f เองนอกจากใช้ฟังก์ชันเกาส์แล้วก็อาจจะใช้ฟังก์ชันแบบอื่นอีก อย่างไรก็ตามในที่นี้จะใช้แต่เกาส์เป็นหลัก
ในที่นี้ r อาจกำหนดให้มีค่าเท่ากับความกว้างของแกนที่กว้างที่สุดของโครงข่าย
..(10)
ส่วน τ ให้เป็น
..(11)
ขั้นตอนและสูตรคำนวณที่ว่ามาทั้งหมดนี้หากอ่านวิธีการจากแหล่งต่างๆกันอาจมีความแตกต่างไปในรายละเอียด อาจมีการปรับแต่งให้เหมาะสมกับงานที่ใช้ แต่หลักการโดยภาพรวมก็จะประมาณนี้
เขียนโครงข่ายมิติเดียว
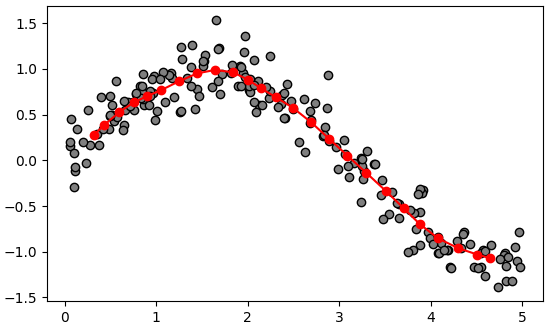
จากขั้นตอนที่อธิบายมาทั้งหมด คราวนี้ลองนำมาใช้เขียนโค้ด เพื่อความเข้าใจง่ายขอเริ่มจากหนึ่งมิติก่อน
ต่อมานำมาสร้างเป็นคลาสให้เป็นระเบียบ
เมธอด rianru ไว้ใช้เริ่มการเรียนรู้เพื่อให้โครงข่ายทำการจัดวางตัวลงบนข้อมูลนั้น
เมธอด plaeng จะทำหน้าที่หาว่าค่าจากพิกัดข้อมูลเดิมนั้นจะไปอยู่ตำแหน่งไหนในโครงข่ายของเรา หรือก็คือการหาว่าจุดนั้นอยู่ใกล้ตำแหน่งของเซลล์ไหนที่สุด
โดยถ้าใส่ค่า ao_rayahang=1 จะให้คืนค่าระยะห่างจากตำแหน่งของเซลล์ใกล้สุดนั้นมาด้วย บางครั้งระยะห่างก็จำเป็นต้องนำมาใช้ไม่อาจละทิ้งได้เหมือนกัน
ส่วน plaengklap จะทำการแปลงค่าตำแหน่งในโครงข่ายไปเป็นตำแหน่งในข้อมูลเดิม เพียงแต่ถ้าไม่ได้ป้อนค่าตำแหน่งไปก็ให้เป็นการหาตำแหน่งของทุกเซลล์บนโครงข่าย
เมธอด rianru_plaeng เอาไว้ใช้สำหรับเรียนรู้เสร็จแล้วก็ทำการแปลงข้อมูลที่ใช้เรียนรู้นั้นไปด้วยเลยทันที
ตัวอย่างการใช้
เขียนโครงข่ายสองมิติขึ้นไป
ต่อมาคราวนี้จะทำการปรับปรุงโค้ดเดิมให้เป็นแบบที่ใช้ในกี่มิติก็ได้ ความซับซ้อนจะเพิ่มขึ้นมาพอสมควรแต่หลักการทั้งหมดเหมือนเดิม
ตัวอย่างการใช้ ลองใช้กับข้อมูลสามมิติซึ่งเป็นค่าสี แดง เขียว น้ำเงิน ให้ SOM ลองวางแผ่นโครงข่ายให้แผ่กระจายทั่วดู
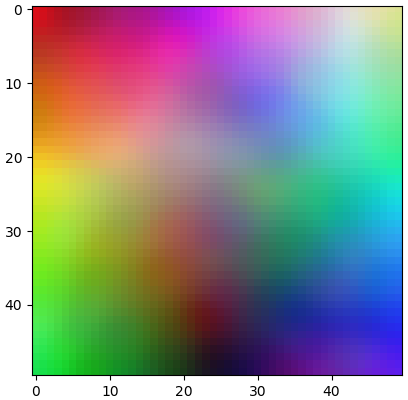
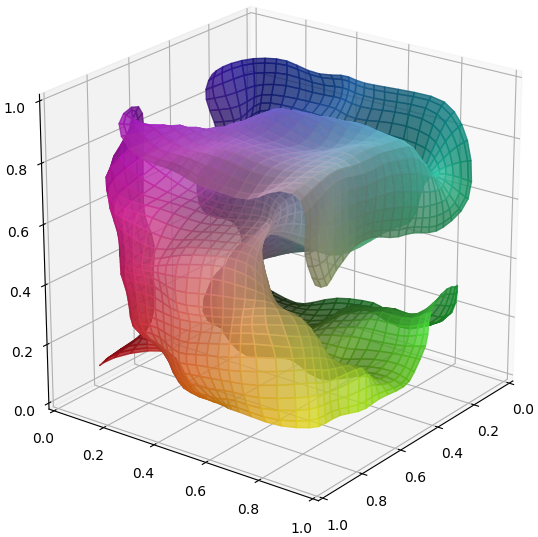
สีบนแผ่นโครงข่ายแสดงถึงสีที่เกิดจากการผสมของแม่สีทั้งสามตามตำแหน่งนั้นจริงๆ ในระนาบสามมิติของค่าสีจะเห็นว่าโครงข่ายแผ่ม้วนไปมาลากผ่านบริเวณต่างๆจนทั่ว สีตามตำแหน่งนั้นถูกแสดงลงในพิกัดของโครงข่ายด้วย
ลองดูภาพเคลื่อนไหวแสดงลำดับความเปลี่ยนแผลงของแผ่นในแต่ละขั้นได้ในนี้ https://www.facebook.com/ikamiso/videos/1782038691893136
ข้อมูลหลายมิติ
ที่ผ่านมาเพื่อให้เห็นภาพการทำงานของ SOM ชัดเจนจึงใช้กับข้อมูลสองหรือสามมิติเป็นหลัก แต่บ่อยครั้งที่ SOM มีไว้ใช้กับข้อมูลที่มีมิติจำนวนมาก ยุบลงมาให้เหลือสองมิติเพื่อให้มองเห็นภาพได้ง่าย
ต่อไปจะลองใช้ข้อมูลไวน์ซึ่งมี ๑๓ มิติเป็นตัวอย่าง (รายละเอียดชุดข้อมูล https://phyblas.hinaboshi.com/20171207)
เนื่องจากข้อมูลทั้ง ๑๓ เป็นคนละหน่วยกันและมีค่าต่างกันมาก จำเป็นต้องปรับค่าทำให้เป็นมาตรฐานก่อนด้วย
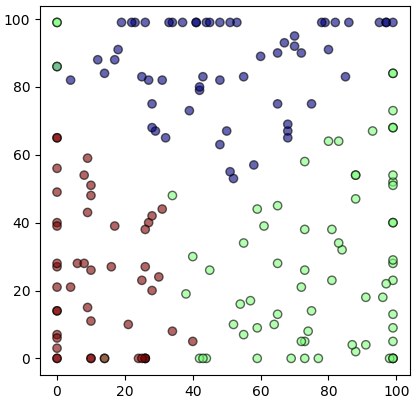
ข้อมูลไวน์ ๑๓ มิติถูกนำมาจัดวางใน ๒ มิติอย่างเรียบร้อย ข้อมูลในแต่ละกลุ่มดูจะวางตัวอยู่ใกล้กันดีแม้จะมีที่หลงกลุ่มอยู่บ้าง
สรุปส่งท้าย
SOM เป็นเทคนิคที่ช่วยแปลงข้อมูลโดยลดมิติจึงมีความคล้ายคลึงกับการวิเคราะห์องค์ประกอบหลัก (主成分分析, principle component Analysis, PCA) (รายละเอียด https://phyblas.hinaboshi.com/20180727) แต่อัลกอริธึมต่างกันมาก และ SOM มักจะจัดข้อมูลให้มีการกระจายทั่วโครงข่าย
และด้วยความที่เป็นการวิเคราะห์และจัดเรียงโครงสร้างภายในของข้อมูล จึงมีความคล้ายคลึงกับพวกเทคนิคการแบ่งกระจุกข้อมูล เช่น วิธีการ k เฉลี่ย (K-平均算法, k-means) (รายละเอียด https://phyblas.hinaboshi.com/20171220)
แต่ต่างกันตรงที่ SOM จะไม่ได้แบ่งข้อมูลออกเป็นกลุ่มๆให้ แค่นำมาจัดเรียงให้อยู่ในหนึ่งหรือสองมิติเพื่อให้เห็นภาพชัด
ข้อมูลในมิติใหม่นี้อาจถูกนำมาใช้เพื่อวิเคราะห์ด้วยเทคนิคต่างๆต่อไปอีกที
อ้างอิง
แนวคิด
SOM เป็นเทคนิคในการวิเคราะห์โครงสร้างของการกระจายตัวของข้อมูลโดยอัตโนมัติ แล้ววาดออกมาเป็นแผนที่แสดงการจัดเรียงของข้อมูลนั้นในพิกัดของแผนที่ที่ถูกสร้างขึ้น
ตัวอย่างเช่นเรามีข้อมูลที่กระจายตัวในสองมิติอยู่ในลักษณะแบบนี้

เราสามารถใช้ SOM หาโครงสร้างการกระจายของข้อมูลแล้วลากเส้นโค้งผ่านกลุ่มข้อมูลเหล่านั้น

แล้วแสดงข้อมูลเหล่านั้นออกมาใหม่ในรูปหนึ่งมิติแบบนี้

ในที่นี้แกนนอนแสดงดัชนีตำแหน่งบนเส้นโค้งที่ใกล้จุดนั้นๆมากที่สุด ส่วนแนวตั้งเป็นระยะห่างระหว่างจุดนั้นกับจุดบนเส้นที่ใกล้สุด
หรือเช่นข้อมูลที่กระจายในสามมิติแบบนี้

เราสามารถใช้ SOM เพื่อสร้างแผ่นผ้าสี่เหลี่ยมโค้งๆเป็นโครงข่ายแผ่พาดผ่านจุดเหล่านี้

แล้วก็แสดงตำแหน่งจุดเหล่านี้ภายในพิกัดของโครงข่ายแผ่นผ้านั้น

โครงสร้างทั้งหมดนี้ อัลกอริธึมของ SOM สามารถทำการหาให้เราได้โดยอัตโนมัติ
SOM มักถูกใช้กับข้อมูลที่มีจำนวนมิติมาก เพื่อทำแผนที่โครงสร้างของข้อมูลนั้นในมิติที่น้อยลง เป็นการลดมิติของข้อมูล และเป็นการทำให้มองเห็นภาพง่ายขึ้น โดยทั่วไปแล้ว SOM นิยมทำเป็นแผ่นสองมิติ ซึ่งมองแล้วก็จะเหมือนเอาข้อมูลทั้งหมดมาจับวางลงบนกระดาษกลายเป็นเหมือนแผ่นแผนที่ให้เห็นว่ากระจายตัวกันยังไง
เทคนิคนี้คิดค้นในปี 1981 โดย เต็วโวะ โกะโฮะเน็น (Teuvo Kohonen) ชาวฟินแลนด์ บางครั้งจึงถูกเรียกว่า แผนที่โกะโฮะเน็น (Kohonen map)
เทคนิคนี้จัดว่าเป็นโครงข่ายประสาทเทียม (人工神经网络, artificial neural network) ชนิดหนึ่ง เพียงแต่ว่าแนวคิดแตกต่างจากโครงข่ายประสาทเทียมซึ่งคนทั่วไปคุ้นเคยซึ่งมีพื้นฐานมาจากเพอร์เซ็ปตรอน
แนวคิด SOM มีพื้นฐานมาจากการเลียนแบบระบบการทำงานของสมองมนุษย์ เซลล์ประสาทในแต่ละส่วนของเปลือกสมองจะมีความไวต่อสิ่งเร้าในรูปแบบต่างๆไม่เท่ากัน แต่ว่าส่วนที่ใกล้กันจะมีแนวโน้มที่จะไวต่ออะไรที่ใกล้เคียงกัน
เส้นโค้งใน SOM 1 มิติ หรือแผ่นผ้าใน SOM 2 มิตินี้มักถูกเรียกว่าเป็นโครงข่ายประสาท โดยแต่ละจุดบนแผ่นหรือเส้นนั้นเรียกว่าเป็นเซลล์ประสาท (neuron)
เพื่อให้สั้นๆและเข้าใจตรงกัน ต่อจากตรงนี้ไปจะเรียกเส้นหรือแผ่นโครงข่ายนี้ว่า "โครงข่าย" เรียกจุดบนโครงข่ายว่า "เซลล์"
อัลกอริธึม
เป้าหมายของ SOM คือการสร้างเส้นโค้งหรือระนาบโค้งที่ลากผ่านใกล้จุดต่างๆได้โดยอัตโนมัติ
วิธีการก็คือ เริ่มแรกสุ่มตำแหน่งของเซลล์ของเส้นโครงข่ายขึ้นมาก่อนแบบสุ่ม จากนั้นก็ค่อยๆทำการปรับไปเรื่อยๆจนสุดท้ายเซลล์ของเส้นโครงข่ายไปวางตัวอยู่บนจุดของข้อมูล ดังภาพนี้

ขั้นตอนมีดังนี้
1. สร้างอาเรย์ตำแหน่งของจุดข้อมูล
..(1)
โดย n คือจำนวนจุดข้อมูล ส่วน m คือมิติของพิกัดข้อมูล
2. สร้างอาเรย์แสดงตำแหน่งภายในพิกัดข้อมูลเดิมของแต่ละเซลล์ของโครงข่าย
..(2)
โดย ν เป็นจำนวนเซลล์ในโครงข่าย
3. สร้างอาเรย์แสดงตำแหน่งเซลล์ภายในพิกัดโครงข่าย
ถ้าเครือข่ายมีมิติเดียวจะได้ว่า
..(3)
ถ้ามีสองมิติจะได้เป็น
..(4)
โดย ν0 คือจำนวนเซลล์ตามแกนตั้ง ν1 คือจำนวนเซลล์ตามแกนนอน ในที่นี้จำนวนเซลล์รวมทั้งหมดคือ ν = ν0×ν1
4. หยิบจุดข้อมูลจุดหนึ่งขึ้นมาพิจารณา คำนวณหาระยะทางแล้วดูว่าเซลล์ไหนบนโครงข่ายอยู่ใกล้จุดนั้นมากที่สุด
ระยะทางโดยทั่วไปแล้วคำนวณแบบยูคลิดธรรมดา คือรากที่สองของผลรวมกำลังสอง
..(5)

5. ย้ายเซลล์ที่อยู่ใกล้สุดบนโครงข่ายนั้นให้เข้าไปใกล้จุดที่พิจารณา โดยเซลล์ที่อยู่ใกล้ๆกันก็จะได้รับอิทธิพลทำให้เคลื่อนเข้าใกล้ไปด้วย ยิ่งเป็นเซลล์ที่อยู่ใกล้กันในพิกัดของโครงข่าย (ค่า c ใกล้กัน) ก็ยิ่งเคลื่อนตามไปมาก
การเปลี่ยนแปลงคำนวณตามนี้
..(6)
โดย f เป็นฟังก์ชันที่แสดงอัตราการเปลี่ยนแปลงโดยค่าจะขึ้นอยู่กับว่าห่างจากเซลล์ใกล้สุดเท่าไหร่ในพิกัดของโครงข่าย
ให้จินตนาการว่าเหมือนเราจับส่วนหนึ่งของเส้นด้ายให้เลื่อนไปบนพื้น ส่วนที่อยู่ใกล้ๆก็จะต้องเลื่อนตามไปด้วย แต่ส่วนไกลๆจะแทบไม่เลื่อนตาม
โดยทั่วไปจะใช้ฟังก์ชันที่ลดลงเรื่อยๆตามระยะห่าง เช่นฟังก์ชันเกาส์
..(7)
โดย c* เป็นตำแหน่งของเซลล์ใกล้สุด
โดย rt เป็นอัตราการลดอิทธิพลตามระยะทาง
ส่วน ηt เป็นอัตราการเรียนรู้
โดยทั่วไปทั้ง rt และ ηt จะไม่คงตัว แต่จะกำหนดให้ยิ่งเวลาผ่านไปก็ยิ่งลดลงไปเรื่อยๆ นั่นหมายถึงยิ่งเวลาผ่านไปการเปลี่ยนแปลงก็จะยิ่งน้อย
ภาพนี้แสดงจุดที่พิจารณาและเซลล์ใกล้สุดโดยล้อมด้วยกรอบแดงและเชื่อมด้วยเส้นแดง ส่วนสีของจุดเซลล์บนเส้นโครงข่ายแสดงระดับอิทธิพล ยิ่งอยู่ในลำดับใกล้กับเซลล์ใกล้สุดก็ยิ่งเป็นสีเขียว และจะมีการเลื่อนตำแหน่งมาก รูปล่างแสดงตำแหน่งหลังเลื่อนไปแล้ว


6. ทำซ้ำข้อ 4. ไปเรื่อยๆโดยเปลี่ยนจุดข้อมูลที่พิจารณา

7. พอใช้จุดข้อมูลครบทุกจุดก็วนกลับมาใช้จุดเดิมใหม่ โดยในรอบใหม่นี้อัตราการเรียนรู้จะลดลงเรื่อยๆในแต่ละรอบ แล้วก็ทำซ้ำใหม่ไปเรื่อยๆจนครบจำนวนครั้งที่ต้องการ
rt และ ηt อาจกำหนดให้ลดลงเรื่อยๆแบบเอกซ์โพเนนเชียล
..(8)
..(9)
τ เป็นอัตราการลดค่าตามเวลา
จากขั้นตอนทั้งหมดนี้จะเห็นว่ามีไฮเพอร์พารามิเตอร์ที่ต้องปรับอยู่ ๔ ตัวคือ
- ขนาดของโครงข่าย ν
- อัตราการเรียนรู้ตั้งต้น η
- r
- τ
นอกจากนี้ฟังก์ชัน f เองนอกจากใช้ฟังก์ชันเกาส์แล้วก็อาจจะใช้ฟังก์ชันแบบอื่นอีก อย่างไรก็ตามในที่นี้จะใช้แต่เกาส์เป็นหลัก
ในที่นี้ r อาจกำหนดให้มีค่าเท่ากับความกว้างของแกนที่กว้างที่สุดของโครงข่าย
..(10)
ส่วน τ ให้เป็น
..(11)
ขั้นตอนและสูตรคำนวณที่ว่ามาทั้งหมดนี้หากอ่านวิธีการจากแหล่งต่างๆกันอาจมีความแตกต่างไปในรายละเอียด อาจมีการปรับแต่งให้เหมาะสมกับงานที่ใช้ แต่หลักการโดยภาพรวมก็จะประมาณนี้
เขียนโครงข่ายมิติเดียว
จากขั้นตอนที่อธิบายมาทั้งหมด คราวนี้ลองนำมาใช้เขียนโค้ด เพื่อความเข้าใจง่ายขอเริ่มจากหนึ่งมิติก่อน
import numpy as np
import matplotlib.pyplot as plt
# จุดข้อมูลในสองมิติ
x = np.random.uniform(0,5,200)
y = np.random.normal(np.sin(x),0.2)
X = np.array([x,y]).T
plt.axes(aspect=1)
plt.scatter(x,y,c='C7',edgecolor='k',cmap='rainbow')
nu = 25 # จำนวนจุดในโครงข่าย ν
eta = 0.5 # อัตราการเรียนรู้ตั้งต้น
thamsam = 20 # จำนวนครั้งที่ทำซ้ำ
tau = thamsam/np.log(nu) # τ
w = [np.random.uniform(X[:,i].min(),X[:,i].max(),nu) for i in range(X.shape[1])]
w = np.array(w).T # ตำแหน่งจุดของโครงข่ายภายในพิกัดข้อมูลเดิม
c = np.arange(nu) # ตำแหน่งจุดของโครงข่ายภายในพิกัดโครงข่าย
for t in range(thamsam):
e = np.exp(-t/tau)
r_t = nu*e
eta_t = eta*e
for Xi in np.random.permutation(X):
Xi_w = Xi-w
raya2 = (Xi_w**2).sum(1) # ระยะห่างกำลังสองระหว่างแต่ละเซลล์กับจุดที่พิจารณา
c_klaisut = np.argmin(raya2) # เซลล์ใกล้สุด
d2 = (c-c_klaisut)**2 # ระยะห่างกำลังสองจากจุดใกล้สุดในพิกัดโครงข่าย
f = np.exp(-0.5*d2/r_t**2)
w += (eta_t*f)[:,None] * Xi_w # ปรับค่า w
plt.plot(w[:,0],w[:,1],'-or') # วาดจุดโครงข่าย
plt.show()
ต่อมานำมาสร้างเป็นคลาสให้เป็นระเบียบ
class SOM_1miti:
def __init__(self,nu=50,eta=0.1):
self.nu = nu
self.eta = eta
def rianru(self,X,n_thamsam=100):
self.tau = n_thamsam/np.log(self.nu)
w = [np.random.uniform(X[:,i].min(),X[:,i].max(),nu) for i in range(X.shape[1])]
self.w = w = np.array(w).T
c = np.arange(self.nu)
for t in range(thamsam):
e = np.exp(-t/tau)
r_t = nu*e
eta_t = eta*e
for Xi in np.random.permutation(X):
Xi_w = Xi-w
raya2 = (Xi_w**2).sum(1)
c_klaisut = np.argmin(raya2)
d2 = (c-c_klaisut)**2
f = np.exp(-0.5*d2/r_t**2)
w += (eta_t*f)[:,None] * Xi_w
def plaeng(self,X,ao_rayahang=0):
if(X.ndim==1):
x_w = X-self.w
i = np.argmin((x_w**2).sum(1))
if(ao_rayahang):
return i,np.sqrt((x_w[i]**2).sum())
else:
return i
else:
if(ao_rayahang):
c_klai = []
rayahang2 = []
for x_w_2 in ((X[:,None]-self.w)**2).sum(2):
i = np.argmin(x_w_2)
c_klai.append(i)
rayahang2.append(x_w_2[i])
rayahang = np.sqrt(np.array(rayahang2))
return np.array(c_klai),rayahang
else:
return np.array([np.argmin(x_w_2) for x_w_2 in ((X[:,None]-self.w)**2).sum(2)])
def plaengklap(self,c=None):
if(c==None):
return self.w
else:
return self.w[c]
def rianru_plaeng(self,X,n_thamsam=100,ao_rayahang=0):
self.rianru(X,n_thamsam)
return self.plaeng(X,ao_rayahang)เมธอด rianru ไว้ใช้เริ่มการเรียนรู้เพื่อให้โครงข่ายทำการจัดวางตัวลงบนข้อมูลนั้น
เมธอด plaeng จะทำหน้าที่หาว่าค่าจากพิกัดข้อมูลเดิมนั้นจะไปอยู่ตำแหน่งไหนในโครงข่ายของเรา หรือก็คือการหาว่าจุดนั้นอยู่ใกล้ตำแหน่งของเซลล์ไหนที่สุด
โดยถ้าใส่ค่า ao_rayahang=1 จะให้คืนค่าระยะห่างจากตำแหน่งของเซลล์ใกล้สุดนั้นมาด้วย บางครั้งระยะห่างก็จำเป็นต้องนำมาใช้ไม่อาจละทิ้งได้เหมือนกัน
ส่วน plaengklap จะทำการแปลงค่าตำแหน่งในโครงข่ายไปเป็นตำแหน่งในข้อมูลเดิม เพียงแต่ถ้าไม่ได้ป้อนค่าตำแหน่งไปก็ให้เป็นการหาตำแหน่งของทุกเซลล์บนโครงข่าย
เมธอด rianru_plaeng เอาไว้ใช้สำหรับเรียนรู้เสร็จแล้วก็ทำการแปลงข้อมูลที่ใช้เรียนรู้นั้นไปด้วยเลยทันที
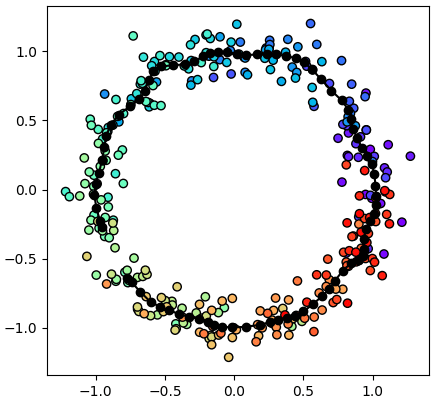
ตัวอย่างการใช้
n = 300
theta = np.random.normal(np.linspace(0,360,n),25)
r = np.random.normal(1,0.1,n)
x = np.cos(np.radians(theta))*r
y = np.sin(np.radians(theta))*r
X = np.array([x,y]).T
si = np.linspace(0,1,n)
nu = 80
eta = 0.5
n_thamsam = 100
som = SOM_1miti(nu,eta)
som.rianru(X,n_thamsam) # เรียนรู้
x_,y_ = som.plaeng(X,1) # แปลง โดยให้คืนค่าระยะห่างมาด้วย
# หรือเขียนควบ ๒ ขั้นตอนด้วย x_,y_ = som.rianru_plaeng(X,thamsam,1)
w = som.plaengklap()
plt.axes(aspect=1)
plt.scatter(x,y,c=si,edgecolor='k',cmap='rainbow') # จุดข้อมูล
plt.plot(w[:,0],w[:,1],'-ok') # จุดโครงข่าย
plt.figure()
plt.scatter(x_,y_,c=si,edgecolor='k',cmap='rainbow') # จุดข้อมูลในพิกัดของโครงข่าย
plt.xlabel(u'ตำแหน่งบนเส้น',family='Tahoma',size=14)
plt.ylabel(u'ระยะห่าง',family='Tahoma',size=14)
plt.show()

เขียนโครงข่ายสองมิติขึ้นไป
ต่อมาคราวนี้จะทำการปรับปรุงโค้ดเดิมให้เป็นแบบที่ใช้ในกี่มิติก็ได้ ความซับซ้อนจะเพิ่มขึ้นมาพอสมควรแต่หลักการทั้งหมดเหมือนเดิม
class SOM:
def __init__(self,ruprang=(20,20),eta=0.1):
if(type(ruprang)==int):
self.ruprang = [ruprang]
else:
self.ruprang = ruprang
self.eta = eta
self.miti = len(ruprang)
self.r = max(self.ruprang)
def rianru(self,X,n_thamsam=100):
self.tau = n_thamsam/np.log(self.r)
w = [np.random.uniform(X[:,i].min(),X[:,i].max(),np.prod(self.ruprang)) for i in range(X.shape[1])]
self.w = w = np.array(w).T
c = np.meshgrid(*[np.arange(i) for i in self.ruprang],indexing='ij')
self.c = c = np.stack(c,-1).reshape(-1,self.miti)
for t in range(n_thamsam):
e = np.exp(-t/self.tau)
self.r_t = self.r*e
self.eta_t = self.eta*e
for x in np.random.permutation(X):
x_w = x-w
i = np.argmin((x_w**2).sum(1))
c_klaisut = self.c[i]
d2 = ((self.c-c_klaisut)**2).sum(1)
f = np.exp(-0.5*d2/self.r_t**2)
w += (self.eta_t*f)[:,None]*x_w
def plaeng(self,X,ao_rayahang=0):
if(X.ndim==1):
x_w = X-self.w
i = np.argmin((x_w**2).sum(1))
if(ao_rayahang):
return self.c[i],np.sqrt((x_w[i]**2).sum())
else:
return self.c[i]
else:
if(ao_rayahang):
w_klai = []
rayahang2 = []
for x_w_2 in ((X[:,None]-self.w)**2).sum(2):
i = np.argmin(x_w_2)
w_klai.append(self.c[i])
rayahang2.append(x_w_2[i])
rayahang = np.sqrt(np.array(rayahang2))
return np.array(w_klai),rayahang
else:
return np.array([self.c[np.argmin(x_w_2)] for x_w_2 in ((X[:,None]-self.w)**2).sum(2)])
def plaengklap(self,c=None):
w = self.w.reshape(list(self.ruprang)+[-1])
if(c==None):
return w.transpose(np.arange(self.miti-1,-2,-1))
elif(c.ndim==1):
return w[tuple(c)]
else:
return np.array([w[tuple(ci)] for ci in c])
def rianru_plaeng(self,X,n_thamsam=100,ao_rayahang=0):
self.rianru(X,n_thamsam)
return self.plaeng(X,ao_rayahang)ตัวอย่างการใช้ ลองใช้กับข้อมูลสามมิติซึ่งเป็นค่าสี แดง เขียว น้ำเงิน ให้ SOM ลองวางแผ่นโครงข่ายให้แผ่กระจายทั่วดู
X = np.random.random([1000,3])
ruprang = [50,50]
som = SOM(ruprang,0.1)
som.rianru(X,200)
Xsom,h = som.plaeng(X,1)
m = som.plaengklap()
from mpl_toolkits.mplot3d import Axes3D
plt.imshow(m)
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[0,1],ylim=[0,1],zlim=[0,1])
ax.plot_surface(m[:,:,0],m[:,:,1],m[:,:,2],facecolors=m,rstride=1,cstride=1,alpha=0.8,color='b',edgecolor='k')
plt.show()

สีบนแผ่นโครงข่ายแสดงถึงสีที่เกิดจากการผสมของแม่สีทั้งสามตามตำแหน่งนั้นจริงๆ ในระนาบสามมิติของค่าสีจะเห็นว่าโครงข่ายแผ่ม้วนไปมาลากผ่านบริเวณต่างๆจนทั่ว สีตามตำแหน่งนั้นถูกแสดงลงในพิกัดของโครงข่ายด้วย
ลองดูภาพเคลื่อนไหวแสดงลำดับความเปลี่ยนแผลงของแผ่นในแต่ละขั้นได้ในนี้ https://www.facebook.com/ikamiso/videos/1782038691893136
ข้อมูลหลายมิติ
ที่ผ่านมาเพื่อให้เห็นภาพการทำงานของ SOM ชัดเจนจึงใช้กับข้อมูลสองหรือสามมิติเป็นหลัก แต่บ่อยครั้งที่ SOM มีไว้ใช้กับข้อมูลที่มีมิติจำนวนมาก ยุบลงมาให้เหลือสองมิติเพื่อให้มองเห็นภาพได้ง่าย
ต่อไปจะลองใช้ข้อมูลไวน์ซึ่งมี ๑๓ มิติเป็นตัวอย่าง (รายละเอียดชุดข้อมูล https://phyblas.hinaboshi.com/20171207)
เนื่องจากข้อมูลทั้ง ๑๓ เป็นคนละหน่วยกันและมีค่าต่างกันมาก จำเป็นต้องปรับค่าทำให้เป็นมาตรฐานก่อนด้วย
from sklearn import datasets
wine = datasets.load_wine()
X = wine.data
X = (X-X.mean(0))/X.std(0)
Xsom = SOM([100,100],eta=0.1).rianru_plaeng(X,100)
plt.axes(aspect=1)
plt.scatter(Xsom[:,0],Xsom[:,1],c=wine.target,alpha=0.6,edgecolor='k',cmap='jet')
plt.show()
ข้อมูลไวน์ ๑๓ มิติถูกนำมาจัดวางใน ๒ มิติอย่างเรียบร้อย ข้อมูลในแต่ละกลุ่มดูจะวางตัวอยู่ใกล้กันดีแม้จะมีที่หลงกลุ่มอยู่บ้าง
สรุปส่งท้าย
SOM เป็นเทคนิคที่ช่วยแปลงข้อมูลโดยลดมิติจึงมีความคล้ายคลึงกับการวิเคราะห์องค์ประกอบหลัก (主成分分析, principle component Analysis, PCA) (รายละเอียด https://phyblas.hinaboshi.com/20180727) แต่อัลกอริธึมต่างกันมาก และ SOM มักจะจัดข้อมูลให้มีการกระจายทั่วโครงข่าย
และด้วยความที่เป็นการวิเคราะห์และจัดเรียงโครงสร้างภายในของข้อมูล จึงมีความคล้ายคลึงกับพวกเทคนิคการแบ่งกระจุกข้อมูล เช่น วิธีการ k เฉลี่ย (K-平均算法, k-means) (รายละเอียด https://phyblas.hinaboshi.com/20171220)
แต่ต่างกันตรงที่ SOM จะไม่ได้แบ่งข้อมูลออกเป็นกลุ่มๆให้ แค่นำมาจัดเรียงให้อยู่ในหนึ่งหรือสองมิติเพื่อให้เห็นภาพชัด
ข้อมูลในมิติใหม่นี้อาจถูกนำมาใช้เพื่อวิเคราะห์ด้วยเทคนิคต่างๆต่อไปอีกที
อ้างอิง
https://ja.wikipedia.org/wiki/自己組織化写像
https://qiita.com/T_Shinaji/items/609fe9aabd99c287b389
http://www.sist.ac.jp/~kanakubo/research/neuro/selforganizingmap.html
http://technocrat.hatenablog.com/entry/2015/02/12/014557
http://blog.xuite.net/metafun/life/509048033
http://alaric-research.blogspot.tw/2011/02/self-organizing-map.html
http://www.ziyoubaba.com/archives/606
http://blog.csdn.net/xbinworld/article/details/50818803
http://blog.csdn.net/u014028027/article/details/72458117
https://qiita.com/T_Shinaji/items/609fe9aabd99c287b389
http://www.sist.ac.jp/~kanakubo/research/neuro/selforganizingmap.html
http://technocrat.hatenablog.com/entry/2015/02/12/014557
http://blog.xuite.net/metafun/life/509048033
http://alaric-research.blogspot.tw/2011/02/self-organizing-map.html
http://www.ziyoubaba.com/archives/606
http://blog.csdn.net/xbinworld/article/details/50818803
http://blog.csdn.net/u014028027/article/details/72458117
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib