[python] การแบ่งกระจุกข้อมูลด้วยวิธีการ k เฉลี่ย
เขียนเมื่อ 2017/12/20 20:02
แก้ไขล่าสุด 2022/07/19 08:42
การเรียนรู้ของเครื่องแบบไม่มีผู้สอนมีวิธีอยู่หลากหลาย ดังที่ได้อธิบายไปใน https://phyblas.hinaboshi.com/20171215
ในบทความนี้จะอธิบายถึงวิธีการเรียนรู้แบบไม่มีผู้สอนที่น่าจะถือว่าได้รับความนิยมกันมากที่สุด นั่นก็คือ วิธีการ k เฉลี่ย (K-平均算法, k-means)
วิธีการนี้มีความคล้ายคลึงกับวิธีการเพื่อนบ้านใกล้สุด k ตัว ซึ่งเคยเขียนถึงไปก่อนหน้าใน https://phyblas.hinaboshi.com/20171028
เพียงแต่ว่าวิธีการเพื่อนบ้านใกล้สุด k ตัวนั้นเป็นการเรียนรู้แบบมีผู้สอน ดังนั้นแม้ดูเผินๆจะคล้ายกัน แต่จริงๆแล้วเป็นคนละเรื่อง จึงไม่ควรสับสน
ขอเริ่มด้วยการยกตัวอย่างด้วยข้อมูลที่มีลักษณะเป็นกระจุกก้อน ๓ ก้อนดังในรูปนี้
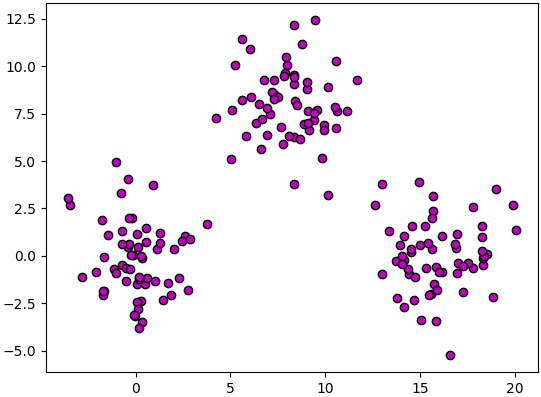
ซึ่งสร้างและวาดภาพได้จากโค้ดนี้
จะเห็นว่าดูด้วยตาก็เห็นได้ว่าแบ่งออกเป็น ๓ กระจุกอย่างชัดเจน แต่เราจะเขียนโปรแกรมยังไงให้มันทำการแบ่งว่าจุดไหนอยู่กระจุกไหนได้โดยอัตโนมัติ
วิธีการคิดง่ายๆอย่างหนึ่งก็คือ ตั้งจุดศูนย์กลางขึ้นมา ๓ จุด แล้วก็วัดว่าจุดไหนอยู่ใกล้ศูนย์กลางอันไหนมากที่สุดก็จัดอยู่ในกลุ่มนั้น
เพียงแต่ว่าจุดศูนย์กลางที่เลือกนั้นจะต้องเหมาะสมด้วย ดังนั้นจึงต้องหาวิธีหาจุดศูนย์กลางที่เหมาะ
จุดศูนย์กลางที่ว่านี้มีชื่อเรียกว่าจุดเซนทรอยด์ (centroid)
วิธีการหาจุดเซนทรอยด์เป็นไปตามขั้นตอนนี้
1. สุ่มจุดเซนทรอยด์เริ่มต้นตามจำนวนที่ต้องการแบ่ง โดยแต่ละจุดใช้ตำแหน่งเป็นจุดข้อมูลสักจุดซึ่งเลือกแบบสุ่ม
2. คำนวณระยะห่างระหว่างทุกจุดข้อมูลไปยังจุดเซนทรอยด์แต่ละจุด
3. จัดกลุ่มให้จุดข้อมูลนั้นอยู่ในกลุ่มของเซนทรอยด์ที่ใกล้สุด
4. ย้ายจุดเซนทรอยด์ไปยังใจกลางของข้อมูลที่ถูกจัดอยู่ในกลุ่มนั้น
5. ทำซ้ำตั้งแต่ขั้นตอนที่ 2. ใหม่โดยใช้เซนทรอยด์ใหม่ที่ได้
6. ทำจนกว่าเซนทรอยด์จะไม่มีการย้ายตำแหน่งไปไหนอีกแล้ว ก็เป็นอันสิ้นสุด
เพียงแต่ว่าไม่ใช่ว่าเซนทรอยด์จะลู่เข้าสู่ค่าใดค่าหนึ่งเสมอไป ดังนั้นจึงต้องกำหนดจำนวนทำครั้งสูงสุด ไม่ให้มันวนซ้ำไม่สิ้นสุด หรือไม่ก็กำหนดค่าความเปลี่ยนแปลงต่ำสุดที่พอใจจะให้หยุดได้ไว้ด้วย
อีกปัญหาหนึ่งที่ต้องคิดก็คือ หากทำไปทำมามีจุดเซนทรอยด์ไหนที่ไม่มีสมาชิกอยู่ในกลุ่มเลยเกิดขึ้นมา มันอาจจะว่างไปตลอดจนจบ ดังนั้นจึงอาจแก้โดยระหว่างวนแก้จุดเซนทรอยด์ซ้ำอยู่นั้นหากมีกลุ่มไหนที่ว่างเปล่า ก็ให้สุ่มย้ายจุดเซนทรอยด์ไปยังจุดข้อมูลสักจุดใหม่
โค้ดอาจเขียนได้ดังนี้
เท่านี้ก็จะได้เซนทรอยด์ที่เหมาะสมแล้ว
จากนั้นก็เอาเซนทรอยด์ที่ได้นี้ไปเป็นตัวกำหนดกลุ่มให้แต่ละจุด แล้วดูผลการแบ่งกลุ่มที่ได้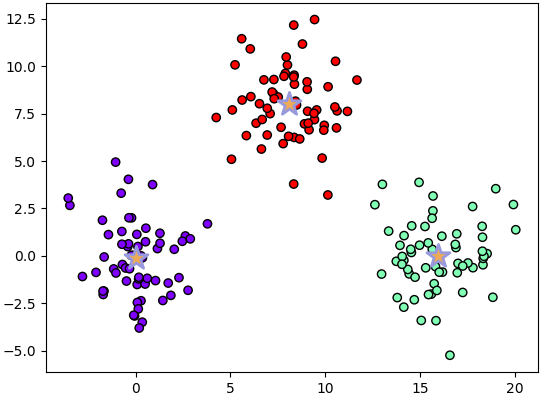
จะเห็นว่ากลุ่มถูกแบ่งออกมาได้เรียบร้อยตามที่ควรเป็น รูปดาวก็คือเซนทรอยด์แต่ละจุด อยู่ใจกลางกระจุกพอดี
แต่ยังมีอีกปัญหาหนึ่งที่ต้องพิจารณา นั่นคือวิธีการนี้ผลที่ได้จะขึ้นอยู่กับจุดเซนทรอยด์ตั้งต้นที่สุ่มได้ กรณีที่สุ่มได้ตำแหน่งไม่ดีตั้งแต่ต้น ผลการแบ่งอาจออกมาได้ไม่ดีดังที่คาดหวังไว้
วิธีหนึ่งที่จะใช้แก้ปัญหาได้ก็คือ ให้ทำใหม่ซ้ำๆหลายครั้ง แล้วเทียบดูว่าครั้งไหนที่แบ่งค่าออกมาได้ดีที่สุดก็ให้ใช้ผลของครั้งนั้น
การจะดูว่าแบ่งออกมาได้ดีแค่ไหนนั้นโดยทั่วไปจะพิจารณาผลรวมของระยะห่างระหว่างจุดข้อมูลไปยังเซนทรอยด์นั้นๆ ซึ่งเรียกว่าผลรวมความคลาดเคลื่อนกำลังสอง (sum of squared errors, SSE)
อาจลองเขียนเป็นโค้ดได้ดังนี้
คราวนี้ลองมาเขียนใหม่ดู โดยยกตัวอย่างเป็นกลุ่มที่แยกกันไม่ชัดเจนมองออกยากหน่อย เช่นแบบนี้
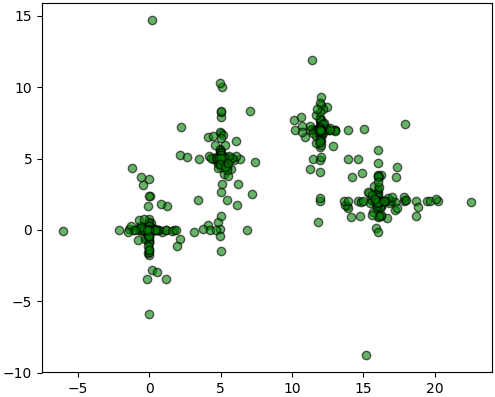
ลองทำสัก ๑๐ ครั้งแล้วเอาอันที่ได้ดีที่สุดมา
โปรแกรมจะพิมพ์ค่า SSE ในแต่ละครั้งออกมา พร้อมทั้งเลือกผลที่ได้ค่าต่ำสุด แล้ววาดรูป
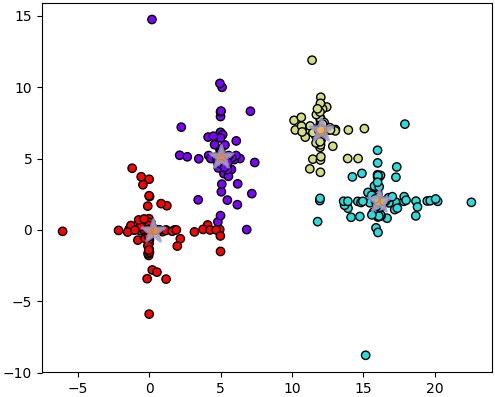
ผลการแบ่งที่ได้จะเห็นว่าออกมาดูดี เพราะเลือกเอาเซนทรอยด์ของครั้งที่แบ่งได้ดีที่สุดมาใช้ คือครั้งที่ได้ค่า SSE เป็น 1432
แต่จะเห็นว่าค่า SSE ที่ได้ออกมาในแต่ละรอบนั้นมีทั้งที่ออกมาได้มากและน้อยต่างกันไป หากลองวาดภาพกรณีอื่นๆที่ไม่ใช่ผลที่ดีที่สุดดู เช่นครั้งที่ได้ 3756 จะได้แบบนี้
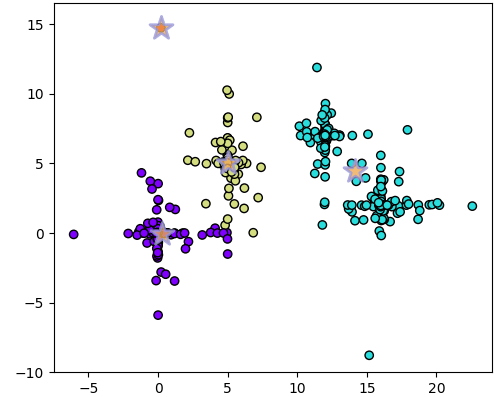
อันนี้ครั้งที่ได้ 3814
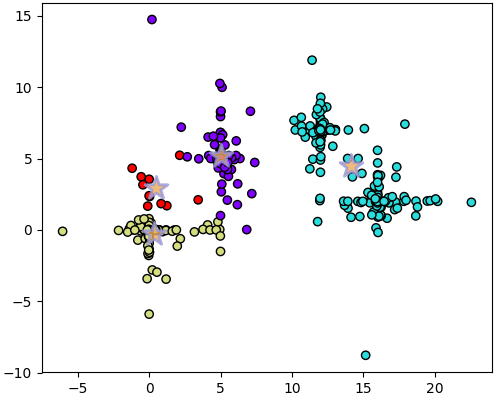
3853
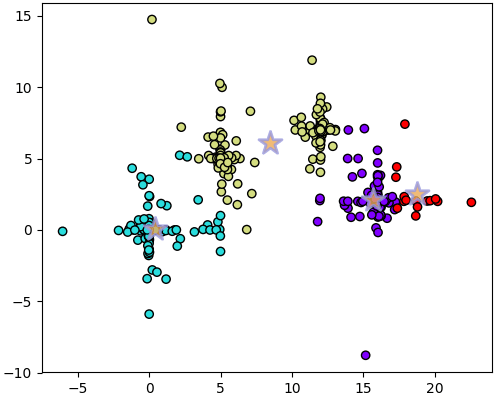
4290
จะเห็นได้ว่าค่า SSE สูงการแบ่งออกมาดูไม่ค่อยดี นั่นเป็นเพราะครั้งนั้นสุ่มได้ตำแหน่งเร่ิมต้นที่ไม่ดี จึงพลาดโอกาสที่จะเจอคำตอบที่ดี
ดังนั้นแล้วเพื่อที่จะหาคำตอบที่ดีที่สุดได้ จึงอาจจะต้องค้นหาซ้ำหลายรอบ
จากนั้นหากนำมาเขียนใหม่ให้อยู่ในรูปแบบของคลาสจะเป็นดังนี้
ผลการแบ่งที่ได้จะออกมาเหมือนกับตอนไม่ใช้คลาส
วิธีการ k เฉลี่ยนั้นใช้การได้ดีกับข้อมูลที่แบ่งเป็นกระจุกก้อนชัดเจนแบบในตัวอย่างที่ยกมาข้างต้น แบบนั้นผลที่ได้จะค่อนข้างแน่นอน
แต่ต่อให้เป็นข้อมูลที่กระจายอย่างไม่มีกลุ่มก้อนแน่นอน ก็สามารถใช้วิธีนี้ให้มันลองแบ่งกลุ่มให้ได้ เช่นข้อมูลลักษณะที่กระจายแทบจะสม่ำเสมอ ถ้าให้คนเราแบ่งเองก็คงไม่รู้จะแบ่งยังไง แต่ถ้าลองใช้วิธี k เฉลี่ยโดยสุ่มจุดเริ่มต้นใหม่หลายๆครั้ง สุดท้ายมันก็จะหาวิธีการแบ่งที่ดูจะเข้าท่าที่สุด (ค่า SSE ต่ำสุด) ออกมาให้ได้
เช่นลองแบ่งข้อมูลที่กระจายสม่ำเสมอแบบนี้ดู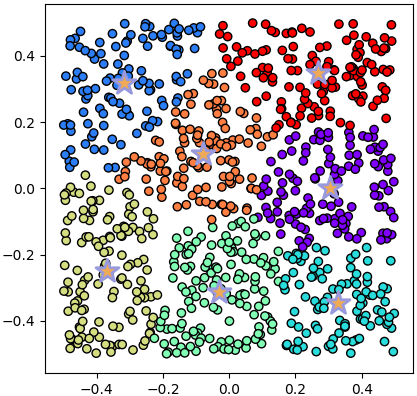
หรือข้อมูลที่ควรจะเป็นกระจุกเดียวแบบนี้
ที่ควรจะต้องระวังอย่างหนึ่งก็คือ ต่อให้ข้อมูลเป็นกระจุกชัดเจนก็ไม่ใช่ว่าจะแบ่งได้เสมอไป ขึ้นอยู่กับรูปร่างของกระจุกด้วย วิธีการนี้จะทำงานได้ดีในกรณีที่กระจุกเป็นทรงกลมชัดเจน แต่ถ้ารูปร่างเรียวยาวก็จะทำได้ไม่ดี
เช่นลองสร้างกระจุกข้อมูลรูปพระจันทร์เสี้ยว (ใช้ฟังก์ชันใน sklearn แนะนำไปใน https://phyblas.hinaboshi.com/20171202)
ที่เป็นแบบนี้เพราะวิธีนี้แบ่งกลุ่มโดยพิจารณาที่ระยะห่างจากเซนทรอยด์ จึงไม่มีทางแบ่งกลุ่มในลักษณะที่ซับซ้อนได้
สำหรับกรณีพระจันทร์เสี้ยวแบบนี้มีวิธีการแบ่งที่เหมาะกว่า ก็คือใช้วิธีที่เรียกว่า DBSCAN ซึ่งเป็นวิธีการแบ่งกลุ่มโดยดูความหนาแน่นของการกระจายข้อมูล
จุดอ่อนอีกอย่างของวิธีการ k เฉลี่ยก็คือจำเป็นจะต้องกำหนดจำนวนกระจุกที่ต้องการแบ่งไว้ตั้งแต่แรก แต่ในปัญหาบางอย่างเราอาจไม่รู้ว่าข้อมูลควรจะแบ่งออกเป็นกี่กระจุกดี ดังนั้นอาจจำเป็นต้องลองทำซ้ำโดยเปลี่ยนจำนวนกระจุกดู
และข้อควรระวังของวิธีนี้ก็คล้ายกับในวิธีการเพื่อนบ้านใกล้สุด k ตัว นั่นคือค่าที่ของสิ่งที่เป็นคนละหน่วยกันควรมีการทำข้อมูลให้เป็นมาตรฐานก่อน
อ้างอิง
ในบทความนี้จะอธิบายถึงวิธีการเรียนรู้แบบไม่มีผู้สอนที่น่าจะถือว่าได้รับความนิยมกันมากที่สุด นั่นก็คือ วิธีการ k เฉลี่ย (K-平均算法, k-means)
วิธีการนี้มีความคล้ายคลึงกับวิธีการเพื่อนบ้านใกล้สุด k ตัว ซึ่งเคยเขียนถึงไปก่อนหน้าใน https://phyblas.hinaboshi.com/20171028
เพียงแต่ว่าวิธีการเพื่อนบ้านใกล้สุด k ตัวนั้นเป็นการเรียนรู้แบบมีผู้สอน ดังนั้นแม้ดูเผินๆจะคล้ายกัน แต่จริงๆแล้วเป็นคนละเรื่อง จึงไม่ควรสับสน
ขอเริ่มด้วยการยกตัวอย่างด้วยข้อมูลที่มีลักษณะเป็นกระจุกก้อน ๓ ก้อนดังในรูปนี้

ซึ่งสร้างและวาดภาพได้จากโค้ดนี้
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(26)
X = np.random.normal(0,1.8,[180,2])
X[60:120] += 8
X[120:,0] += 16
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c='m',edgecolor='k')
plt.show()จะเห็นว่าดูด้วยตาก็เห็นได้ว่าแบ่งออกเป็น ๓ กระจุกอย่างชัดเจน แต่เราจะเขียนโปรแกรมยังไงให้มันทำการแบ่งว่าจุดไหนอยู่กระจุกไหนได้โดยอัตโนมัติ
วิธีการคิดง่ายๆอย่างหนึ่งก็คือ ตั้งจุดศูนย์กลางขึ้นมา ๓ จุด แล้วก็วัดว่าจุดไหนอยู่ใกล้ศูนย์กลางอันไหนมากที่สุดก็จัดอยู่ในกลุ่มนั้น
เพียงแต่ว่าจุดศูนย์กลางที่เลือกนั้นจะต้องเหมาะสมด้วย ดังนั้นจึงต้องหาวิธีหาจุดศูนย์กลางที่เหมาะ
จุดศูนย์กลางที่ว่านี้มีชื่อเรียกว่าจุดเซนทรอยด์ (centroid)
วิธีการหาจุดเซนทรอยด์เป็นไปตามขั้นตอนนี้
1. สุ่มจุดเซนทรอยด์เริ่มต้นตามจำนวนที่ต้องการแบ่ง โดยแต่ละจุดใช้ตำแหน่งเป็นจุดข้อมูลสักจุดซึ่งเลือกแบบสุ่ม
2. คำนวณระยะห่างระหว่างทุกจุดข้อมูลไปยังจุดเซนทรอยด์แต่ละจุด
3. จัดกลุ่มให้จุดข้อมูลนั้นอยู่ในกลุ่มของเซนทรอยด์ที่ใกล้สุด
4. ย้ายจุดเซนทรอยด์ไปยังใจกลางของข้อมูลที่ถูกจัดอยู่ในกลุ่มนั้น
5. ทำซ้ำตั้งแต่ขั้นตอนที่ 2. ใหม่โดยใช้เซนทรอยด์ใหม่ที่ได้
6. ทำจนกว่าเซนทรอยด์จะไม่มีการย้ายตำแหน่งไปไหนอีกแล้ว ก็เป็นอันสิ้นสุด
เพียงแต่ว่าไม่ใช่ว่าเซนทรอยด์จะลู่เข้าสู่ค่าใดค่าหนึ่งเสมอไป ดังนั้นจึงต้องกำหนดจำนวนทำครั้งสูงสุด ไม่ให้มันวนซ้ำไม่สิ้นสุด หรือไม่ก็กำหนดค่าความเปลี่ยนแปลงต่ำสุดที่พอใจจะให้หยุดได้ไว้ด้วย
อีกปัญหาหนึ่งที่ต้องคิดก็คือ หากทำไปทำมามีจุดเซนทรอยด์ไหนที่ไม่มีสมาชิกอยู่ในกลุ่มเลยเกิดขึ้นมา มันอาจจะว่างไปตลอดจนจบ ดังนั้นจึงอาจแก้โดยระหว่างวนแก้จุดเซนทรอยด์ซ้ำอยู่นั้นหากมีกลุ่มไหนที่ว่างเปล่า ก็ให้สุ่มย้ายจุดเซนทรอยด์ไปยังจุดข้อมูลสักจุดใหม่
โค้ดอาจเขียนได้ดังนี้
n_krachuk = 3 # จำนวนกระจุก
n_thamsam = 100 # จำนวนทำซ้ำสูงสุด
tol = 0.0001 # ค่าความเปลี่ยนแปลงสูงสุดที่ยอมให้หยุดได้
sumlueak = np.random.choice(len(X),n_krachuk,replace=0)
X_cen = X[sumlueak] # จุดเซนทรอยด์ตั้งต้น เลือกแบบสุ่ม
# วนซ้ำเพื่อปรับเซนทรอยด์
for i in range(n_thamsam):
raya2 = ((X_cen[None]-X[:,None])**2).sum(2) # วัดระยะห่างจากจุดถึงเซนทรอยด์
klum = raya2.argmin(1) # ตัดสินกลุ่มของจุดโดยเลือกเซนทรอยด์ที่ใกล้สุด
X_cen_mai = np.empty_like(X_cen) # จุดเซนทรอยด์ใหม่
# วนซ้ำเพื่อหาตำแหน่งเซนทรอยด์ใหม่
for j in range(n_krachuk):
if(len(X[klum==j])): # ถ้ามีสมาชิกในกลุ่ม
X_cen_mai[j] = X[klum==j].mean(0) # กำหนดเซนทรอยด์ใหม่เป็นตำแหน่งเฉลี่ยของทุกจุดในกลุ่ม
else: # ถ้าในกลุ่มว่างเปล่าก็ให้สุ่มเซนทรอยด์ใหม่
X_cen_mai[j] = X[np.random.randint(len(X))]
if(np.allclose(X_cen,X_cen_mai,atol=tol)): # ถ้าความเปลี่ยนแปลงน้อยกว่าค่าที่กำหนดก็ให้หยุด
X_cen = X_cen_mai
break
X_cen = X_cen_mai # ย้ายจุดเซนทรอยด์ไปยังตำแหน่งใหม่เท่านี้ก็จะได้เซนทรอยด์ที่เหมาะสมแล้ว
จากนั้นก็เอาเซนทรอยด์ที่ได้นี้ไปเป็นตัวกำหนดกลุ่มให้แต่ละจุด แล้วดูผลการแบ่งกลุ่มที่ได้
raya2 = ((X_cen[None]-X[:,None])**2).sum(2)
z = raya2.argmin(1)
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='rainbow')
plt.scatter(X_cen[:,0],X_cen[:,1],300,'#EEAA55',marker='*',edgecolor='#9999DD',lw=2)
plt.show()
จะเห็นว่ากลุ่มถูกแบ่งออกมาได้เรียบร้อยตามที่ควรเป็น รูปดาวก็คือเซนทรอยด์แต่ละจุด อยู่ใจกลางกระจุกพอดี
แต่ยังมีอีกปัญหาหนึ่งที่ต้องพิจารณา นั่นคือวิธีการนี้ผลที่ได้จะขึ้นอยู่กับจุดเซนทรอยด์ตั้งต้นที่สุ่มได้ กรณีที่สุ่มได้ตำแหน่งไม่ดีตั้งแต่ต้น ผลการแบ่งอาจออกมาได้ไม่ดีดังที่คาดหวังไว้
วิธีหนึ่งที่จะใช้แก้ปัญหาได้ก็คือ ให้ทำใหม่ซ้ำๆหลายครั้ง แล้วเทียบดูว่าครั้งไหนที่แบ่งค่าออกมาได้ดีที่สุดก็ให้ใช้ผลของครั้งนั้น
การจะดูว่าแบ่งออกมาได้ดีแค่ไหนนั้นโดยทั่วไปจะพิจารณาผลรวมของระยะห่างระหว่างจุดข้อมูลไปยังเซนทรอยด์นั้นๆ ซึ่งเรียกว่าผลรวมความคลาดเคลื่อนกำลังสอง (sum of squared errors, SSE)
อาจลองเขียนเป็นโค้ดได้ดังนี้
sse = 0
for i in range(n_krachuk):
sse += np.sum(raya2[z==i,i])
print(sse) # ได้ 1106.13721312sse = (raya2*(z[:,None]==np.arange(n_krachuk))).sum()คราวนี้ลองมาเขียนใหม่ดู โดยยกตัวอย่างเป็นกลุ่มที่แยกกันไม่ชัดเจนมองออกยากหน่อย เช่นแบบนี้
np.random.seed(4)
X = np.random.normal(0,3.,[480,2])**3/60
X[120:240] += 5
X[360:480,0] += 12
X[360:480,1] += 7
X[240:360,0] += 16
X[240:360,1] += 2
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c='g',alpha=0.6,edgecolor='k')
plt.show()
ลองทำสัก ๑๐ ครั้งแล้วเอาอันที่ได้ดีที่สุดมา
n_krachuk = 4
n_thamsam = 50
tol = 0.00001
n_sumchut = 10 # จำนวนครั้งที่สุ่มจุดใหม่
sse_noisut = np.inf # ค่า sse น้อยสุด
for s in range(n_sumchut):
sumlueak = np.random.choice(len(X),n_krachuk,replace=0)
X_cen = X[sumlueak]
for i in range(n_thamsam):
raya2 = ((X_cen[None]-X[:,None])**2).sum(2)
klum = raya2.argmin(1)
X_cen_mai = np.empty_like(X_cen)
for j in range(n_krachuk):
if(len(X[klum==j])):
X_cen_mai[j] = X[klum==j].mean(0)
else:
X_cen_mai[j] = X[np.random.randint(len(X))]
if(np.allclose(X_cen,X_cen_mai,atol=tol)):
X_cen = X_cen_mai
break
X_cen = X_cen_mai
raya2 = ((X_cen[None]-X[:,None])**2).sum(2)
klum = raya2.argmin(1)
# หา sse ในแต่ละรอบ ถ้าได้น้อยกว่าเดิมก็เก็บค่านั้นและตำแหน่งเซนทรอยด์ไว้
sse = (raya2*(klum[:,None]==np.arange(n_krachuk))).sum()
print(sse)
if(sse_noisut>sse):
sse_noisut = sse
X_cen_disut = X_cen
raya2 = ((X_cen_disut[None]-X[:,None])**2).sum(2)
z = raya2.argmin(1)
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='rainbow')
plt.scatter(X_cen_disut[:,0],X_cen_disut[:,1],300,'#EEAA55',alpha=0.8,marker='*',edgecolor='#9999DD',lw=2)
plt.show()โปรแกรมจะพิมพ์ค่า SSE ในแต่ละครั้งออกมา พร้อมทั้งเลือกผลที่ได้ค่าต่ำสุด แล้ววาดรูป
3696.79020957
3814.36451799
1432.78366256
1432.75873231
3853.71442022
1432.78366256
1432.78366256
3756.04317335
4290.05406862
3756.04317335
ผลการแบ่งที่ได้จะเห็นว่าออกมาดูดี เพราะเลือกเอาเซนทรอยด์ของครั้งที่แบ่งได้ดีที่สุดมาใช้ คือครั้งที่ได้ค่า SSE เป็น 1432
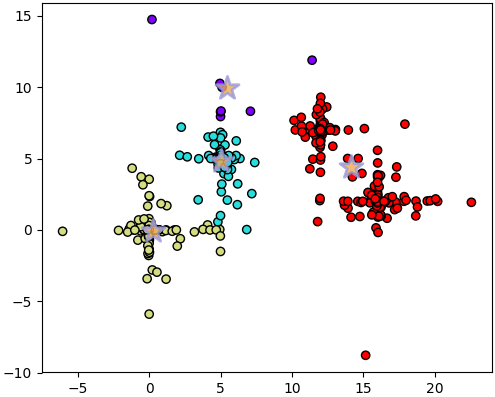
แต่จะเห็นว่าค่า SSE ที่ได้ออกมาในแต่ละรอบนั้นมีทั้งที่ออกมาได้มากและน้อยต่างกันไป หากลองวาดภาพกรณีอื่นๆที่ไม่ใช่ผลที่ดีที่สุดดู เช่นครั้งที่ได้ 3756 จะได้แบบนี้

อันนี้ครั้งที่ได้ 3814

3853

4290

จะเห็นได้ว่าค่า SSE สูงการแบ่งออกมาดูไม่ค่อยดี นั่นเป็นเพราะครั้งนั้นสุ่มได้ตำแหน่งเร่ิมต้นที่ไม่ดี จึงพลาดโอกาสที่จะเจอคำตอบที่ดี
ดังนั้นแล้วเพื่อที่จะหาคำตอบที่ดีที่สุดได้ จึงอาจจะต้องค้นหาซ้ำหลายรอบ
จากนั้นหากนำมาเขียนใหม่ให้อยู่ในรูปแบบของคลาสจะเป็นดังนี้
class Kmeans:
def __init__(self,n_krachuk,n_sumchut=10):
self.n_krachuk = n_krachuk
self.n_sumchut = n_sumchut
def rianru(self,X,n_thamsam=100,tol=0.0001):
sse_noisut = np.inf
for s in range(self.n_sumchut):
sumlueak = np.random.choice(len(X),self.n_krachuk,replace=0)
X_cen = X[sumlueak]
for i in range(n_thamsam):
raya2 = ((X_cen[None]-X[:,None])**2).sum(2)
klum = raya2.argmin(1)
X_cen_mai = np.empty_like(X_cen)
for j in range(self.n_krachuk):
if(len(X[klum==j])):
X_cen_mai[j] = X[klum==j].mean(0)
else:
X_cen_mai[j] = X[np.random.randint(len(X))]
if(np.allclose(X_cen,X_cen_mai,atol=tol)):
break
X_cen = X_cen_mai
X_cen = X_cen_mai
raya2 = ((X_cen[None]-X[:,None])**2).sum(2)
klum = raya2.argmin(1)
sse = (raya2*(klum[:,None]==np.arange(self.n_krachuk))).sum()
if(sse_noisut>sse):
sse_noisut = sse
self.X_cen = X_cen
def thamnai(self,X):
raya2 = ((self.X_cen[None]-X[:,None])**2).sum(2)
return raya2.argmin(1)
np.random.seed(26)
X = np.random.normal(0,1.8,[180,2])
X[60:120] += 8
X[120:,0] += 16
km = Kmeans(n_krachuk=3)
km.rianru(X)
z = km.thamnai(X)
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='rainbow')
plt.scatter(km.X_cen[:,0],km.X_cen[:,1],300,'#EEAA55',marker='*',edgecolor='#9999DD',lw=2)
plt.show()ผลการแบ่งที่ได้จะออกมาเหมือนกับตอนไม่ใช้คลาส
วิธีการ k เฉลี่ยนั้นใช้การได้ดีกับข้อมูลที่แบ่งเป็นกระจุกก้อนชัดเจนแบบในตัวอย่างที่ยกมาข้างต้น แบบนั้นผลที่ได้จะค่อนข้างแน่นอน
แต่ต่อให้เป็นข้อมูลที่กระจายอย่างไม่มีกลุ่มก้อนแน่นอน ก็สามารถใช้วิธีนี้ให้มันลองแบ่งกลุ่มให้ได้ เช่นข้อมูลลักษณะที่กระจายแทบจะสม่ำเสมอ ถ้าให้คนเราแบ่งเองก็คงไม่รู้จะแบ่งยังไง แต่ถ้าลองใช้วิธี k เฉลี่ยโดยสุ่มจุดเริ่มต้นใหม่หลายๆครั้ง สุดท้ายมันก็จะหาวิธีการแบ่งที่ดูจะเข้าท่าที่สุด (ค่า SSE ต่ำสุด) ออกมาให้ได้
เช่นลองแบ่งข้อมูลที่กระจายสม่ำเสมอแบบนี้ดู
def plotkmeans(n,X):
km = Kmeans(n)
km.rianru(X)
z = km.thamnai(X)
plt.figure()
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='rainbow')
plt.scatter(km.X_cen[:,0],km.X_cen[:,1],300,'#EEAA55',marker='*',edgecolor='#9999DD',lw=2)
plt.show()
X = np.random.uniform(-0.5,0.5,[840,2])
plotkmeans(7,X)
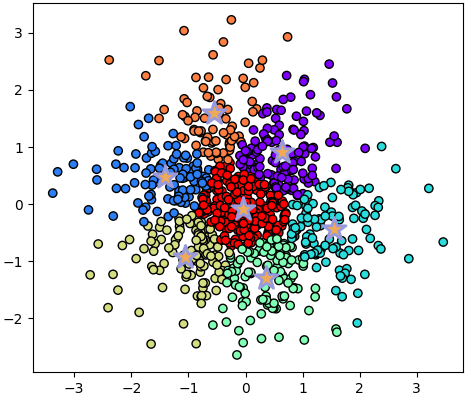
หรือข้อมูลที่ควรจะเป็นกระจุกเดียวแบบนี้
X = np.random.normal(0,1,[840,2])
plotkmeans(7,X)
ที่ควรจะต้องระวังอย่างหนึ่งก็คือ ต่อให้ข้อมูลเป็นกระจุกชัดเจนก็ไม่ใช่ว่าจะแบ่งได้เสมอไป ขึ้นอยู่กับรูปร่างของกระจุกด้วย วิธีการนี้จะทำงานได้ดีในกรณีที่กระจุกเป็นทรงกลมชัดเจน แต่ถ้ารูปร่างเรียวยาวก็จะทำได้ไม่ดี
เช่นลองสร้างกระจุกข้อมูลรูปพระจันทร์เสี้ยว (ใช้ฟังก์ชันใน sklearn แนะนำไปใน https://phyblas.hinaboshi.com/20171202)
from sklearn import datasets
X,_ = datasets.make_moons(n_samples=180,noise=0.05)
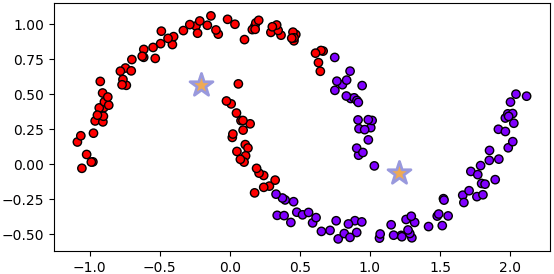
plotkmeans(2,X)
ที่เป็นแบบนี้เพราะวิธีนี้แบ่งกลุ่มโดยพิจารณาที่ระยะห่างจากเซนทรอยด์ จึงไม่มีทางแบ่งกลุ่มในลักษณะที่ซับซ้อนได้
สำหรับกรณีพระจันทร์เสี้ยวแบบนี้มีวิธีการแบ่งที่เหมาะกว่า ก็คือใช้วิธีที่เรียกว่า DBSCAN ซึ่งเป็นวิธีการแบ่งกลุ่มโดยดูความหนาแน่นของการกระจายข้อมูล
จุดอ่อนอีกอย่างของวิธีการ k เฉลี่ยก็คือจำเป็นจะต้องกำหนดจำนวนกระจุกที่ต้องการแบ่งไว้ตั้งแต่แรก แต่ในปัญหาบางอย่างเราอาจไม่รู้ว่าข้อมูลควรจะแบ่งออกเป็นกี่กระจุกดี ดังนั้นอาจจำเป็นต้องลองทำซ้ำโดยเปลี่ยนจำนวนกระจุกดู
และข้อควรระวังของวิธีนี้ก็คล้ายกับในวิธีการเพื่อนบ้านใกล้สุด k ตัว นั่นคือค่าที่ของสิ่งที่เป็นคนละหน่วยกันควรมีการทำข้อมูลให้เป็นมาตรฐานก่อน
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib