maya python เบื้องต้น บทที่ ๑๔: การใช้ฟังก์ชันทางคณิตศาสตร์
เขียนเมื่อ 2016/03/10 21:35
แก้ไขล่าสุด 2021/09/28 16:42
ในภาษาไพธอนมีมอดูลที่สำคัญหลายตัวที่ติดตั้งอยู่ในตัวอยู่แล้ว แต่ต้องใช้คำสั่ง import เพื่อนำเข้ามา
สำหรับบทนี้จะแนะนำมอดูล math ซึ่งมีฟังก์ชันคำนวนทั้งหลายที่จะนำไปใช้ประโยชน์ได้ดี โดยจะยกมาเฉพาะบางส่วน
ก่อนอื่นต้องใช้คำสั่ง import เพื่อเรียกใช้ก่อนจึงจะใช้ได้
ฟังก์ชันตรีโกณมิติ
ตัวผกผันของฟังก์ชันตรีโกณมิติ
ฟังก์ชันไฮเพอร์โบลิก
และฟังก์ชันเอ็กซ์โพเน็นเชียล และลอการิธึม
นอกจากฟังก์ชันแล้ว ในมอดูล math ยังเก็บค่าตัวแปรบางอย่างที่จำเป็นไว้ด้วย เช่น
โดย ทั่วไปแล้วค่ามุมในโปรแกรมมายาจะใช้เป็นหน่วนองศา แต่ว่าในฟังก์ชันคำนวณของภาษาไพธอนจะใช้หน่วยเรเดียนเป็นหลัก ดังนั้นจึงจำเป็นต้องมีการแปลงหน่วยให้สัมพันธ์กัน
การแปลงหน่วยอาจใช้การคูณด้วย math.pi/180 เพื่อแปลงจากองศาเป็นเรเดียน และคูณด้วย 180/math.pi เพื่อแปลงจากองศาเป็นเรเดียน
นอกจากนี้อาจใช้ฟังก์ชันเฉพาะสำหรับการแปลงหน่วย คือ math.degrees() กับ math.radians()
โดย math.degrees(x) จะเปลี่ยนหน่วยของ x จากเรเดียนเป็นองศา
และ math.radians(x) จะเปลี่ยนหน่วยของ x จากองศาเป็นเรเดียน
ลองนำมาประยุกต์ใช้ในมายากันดู
ฟังก์ชันตรีโกณทำให้สามารถนำวัตถุมาเรียงกันเป็นวงกลมได้ เช่น ทำแบบนี้จะได้ลูกบอล 36 ลูกที่เรียงกัน คล้ายสร้อย

ลองตั้งรัศมีให้ไม่เท่ากัน เปลี่ยนไปเป็นคาบก็จะได้รูปร่างสวยไปอีกแบบ

ลองเอามาใช้เพื่อจำลองการสั่นของสปริง ปกติถ้าเอาวัตถุผูกติดกับสปริงตามแนวตั้งแล้วปล่อยวัตถุจะสั่นไปเรื่อยๆ
ในกรณีที่ไม่มีการสูญเสียพลังงาน การกระจัดของสปริงจะเป็นแบบซิมเปิลฮาร์โมนิก คือเป็นฟังก์ชัน sin หรือ cos ในที่นี้ใช้เป็น cos เขียนได้เป็น
x = Acos(2πft)
โดยที่ x คือการกระจัด A คือแอมพลิจูดของการสั่น f คือความถี่การสั่น และ t คือเวลา
เขียนเป็นสมการในภาษาไพธอนได้เป็น
ลองให้ A=10, f=1
แต่โดยทั่วไปแล้วการสั่นมักจะต้องมีการหน่วงเกิดขึ้นทำให้แอมพลิจูดลดลงเรื่อยๆแบบเอ็กซ์โพเน็นเชียล อาจเขียนสมการได้เป็น
โดยเพิ่มส่วนเอ็กซ์โพเน็นเชียบด้านหน้ามา โดย k คือค่าที่ขึ้นกับความหน่วง ยิ่งมากก็ยิ่งทำให้แอมพลิจูดลดลงเร็วขึ้น ในที่นี้ลองให้ k=0.5
ลองเขียนใหม่ โดยคราวนี้เพิ่มตัวสปริงมาด้วย โดยใช้ฟังก์ชัน polyHelix ในการสร้างวัตถุที่เป็นเกลียว
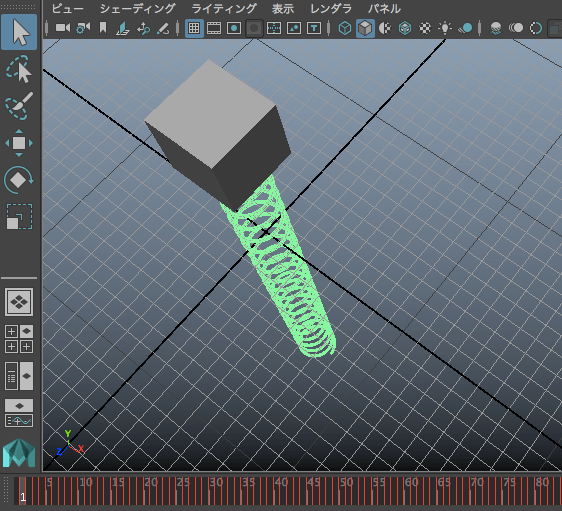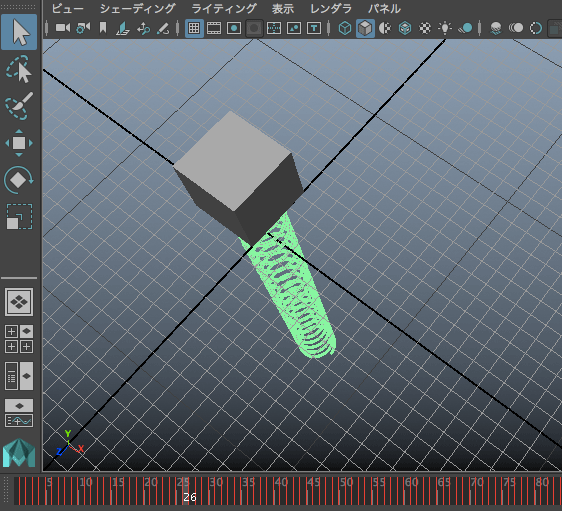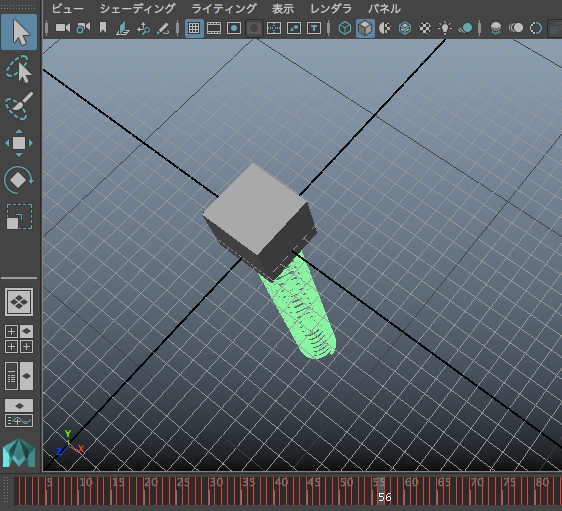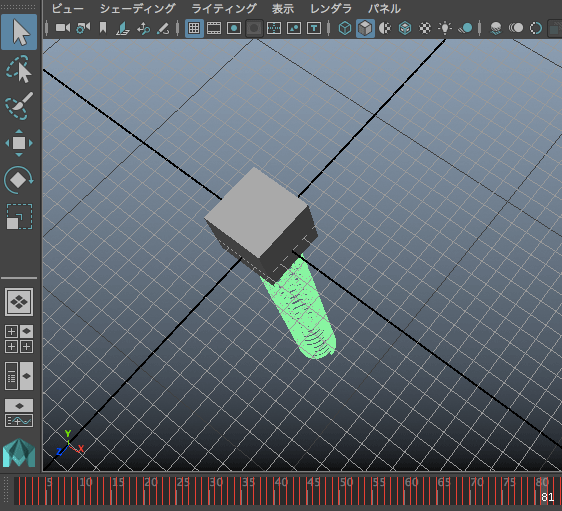
นอกจากนี้ยังอาจลองทำเป็นจำลองคลื่นในเส้นเชือก (คลื่นตามขวาง) โดยให้ทรงกลมหนึ่งลูกแทนมวลในช่วงหนึ่งของเส้นเชือก แล้วสร้างวางเรียงตัวกันไปตามแนวระดับ แต่ละจุดให้มีเฟสเริ่มต้นต่างกัน
ใน บทนี้เราได้ใช้การทำซ้ำเพื่อตั้งคีย์เฟรมลงบนเส้นเวลาอย่างต่อเนื่อง วิธีการนี้ทำให้เกิดจุดบนคีย์เฟรมมากมายทำให้ดูรกและแก้ไขตอนหลังได้ยาก
ที่ จริงแล้วในกรณีที่มีการเปลี่ยนแปลงเป็นฟังก์ชันที่แน่นอนแบบนี้มีวิธีที่ดี กว่านั้นอยู่ นั่นคือการใช้เอ็กซ์เพรชชัน ซึ่งจะพูดถึงในบทต่อไป
เกี่ยวกับฟังก์ชันอื่นๆเพิ่มเติมในมอดูล math อ่านได้ใน https://phyblas.hinaboshi.com/tsuchinoko16
อ้างอิง
สำหรับบทนี้จะแนะนำมอดูล math ซึ่งมีฟังก์ชันคำนวนทั้งหลายที่จะนำไปใช้ประโยชน์ได้ดี โดยจะยกมาเฉพาะบางส่วน
ก่อนอื่นต้องใช้คำสั่ง import เพื่อเรียกใช้ก่อนจึงจะใช้ได้
import math
ฟังก์ชันตรีโกณมิติ
math.sin(x)
math.cos(x)
math.tan(x)
math.cos(x)
math.tan(x)
ตัวผกผันของฟังก์ชันตรีโกณมิติ
math.asin(x)
math.acos(x)
math.atan(x)
math.acos(x)
math.atan(x)
ฟังก์ชันไฮเพอร์โบลิก
math.sinh(x)
math.cosh(x)
math.tanh(x)
math.asinh(x)
math.acosh(x)
math.atanh(x)
math.cosh(x)
math.tanh(x)
math.asinh(x)
math.acosh(x)
math.atanh(x)
และฟังก์ชันเอ็กซ์โพเน็นเชียล และลอการิธึม
math.exp(x)
math.log(x[,ฐาน])
math.log(x[,ฐาน])
นอกจากฟังก์ชันแล้ว ในมอดูล math ยังเก็บค่าตัวแปรบางอย่างที่จำเป็นไว้ด้วย เช่น
math.pi # ค่า π
math.e # ค่าเอ็กซ์โพเน็นเชียล
math.e # ค่าเอ็กซ์โพเน็นเชียล
โดย ทั่วไปแล้วค่ามุมในโปรแกรมมายาจะใช้เป็นหน่วนองศา แต่ว่าในฟังก์ชันคำนวณของภาษาไพธอนจะใช้หน่วยเรเดียนเป็นหลัก ดังนั้นจึงจำเป็นต้องมีการแปลงหน่วยให้สัมพันธ์กัน
การแปลงหน่วยอาจใช้การคูณด้วย math.pi/180 เพื่อแปลงจากองศาเป็นเรเดียน และคูณด้วย 180/math.pi เพื่อแปลงจากองศาเป็นเรเดียน
นอกจากนี้อาจใช้ฟังก์ชันเฉพาะสำหรับการแปลงหน่วย คือ math.degrees() กับ math.radians()
โดย math.degrees(x) จะเปลี่ยนหน่วยของ x จากเรเดียนเป็นองศา
และ math.radians(x) จะเปลี่ยนหน่วยของ x จากองศาเป็นเรเดียน
ลองนำมาประยุกต์ใช้ในมายากันดู
ฟังก์ชันตรีโกณทำให้สามารถนำวัตถุมาเรียงกันเป็นวงกลมได้ เช่น ทำแบบนี้จะได้ลูกบอล 36 ลูกที่เรียงกัน คล้ายสร้อย
import math
for i in range(36):
mc.polySphere(r=1)
mc.move(10*math.cos(math.radians(i*10)),0,10*math.sin(math.radians(i*10)))
for i in range(36):
mc.polySphere(r=1)
mc.move(10*math.cos(math.radians(i*10)),0,10*math.sin(math.radians(i*10)))

ลองตั้งรัศมีให้ไม่เท่ากัน เปลี่ยนไปเป็นคาบก็จะได้รูปร่างสวยไปอีกแบบ
import math
for i in range(36):
mc.polySphere(r=1+math.cos(4*math.radians(i*10))**2)
mc.move(10*math.cos(math.radians(i*10)),0,10*math.sin(math.radians(i*10)))
for i in range(36):
mc.polySphere(r=1+math.cos(4*math.radians(i*10))**2)
mc.move(10*math.cos(math.radians(i*10)),0,10*math.sin(math.radians(i*10)))

ลองเอามาใช้เพื่อจำลองการสั่นของสปริง ปกติถ้าเอาวัตถุผูกติดกับสปริงตามแนวตั้งแล้วปล่อยวัตถุจะสั่นไปเรื่อยๆ
ในกรณีที่ไม่มีการสูญเสียพลังงาน การกระจัดของสปริงจะเป็นแบบซิมเปิลฮาร์โมนิก คือเป็นฟังก์ชัน sin หรือ cos ในที่นี้ใช้เป็น cos เขียนได้เป็น
x = Acos(2πft)
โดยที่ x คือการกระจัด A คือแอมพลิจูดของการสั่น f คือความถี่การสั่น และ t คือเวลา
เขียนเป็นสมการในภาษาไพธอนได้เป็น
x = A*math.cos(2*math.pi*f*t)
ลองให้ A=10, f=1
import math
mc.polyCube(w=4,h=4,d=4,n='watthu')
A=10
f=1
for j in range(1,5*25+2):
t = (j-1.)/25
x = A*math.cos(2*math.pi*f*t)
mc.setKeyframe('watthu',at='ty',v=x,t=j)
mc.polyCube(w=4,h=4,d=4,n='watthu')
A=10
f=1
for j in range(1,5*25+2):
t = (j-1.)/25
x = A*math.cos(2*math.pi*f*t)
mc.setKeyframe('watthu',at='ty',v=x,t=j)

แต่โดยทั่วไปแล้วการสั่นมักจะต้องมีการหน่วงเกิดขึ้นทำให้แอมพลิจูดลดลงเรื่อยๆแบบเอ็กซ์โพเน็นเชียล อาจเขียนสมการได้เป็น
x = math.exp(-k*t)*A*math.cos(2*math.pi*f*t)
โดยเพิ่มส่วนเอ็กซ์โพเน็นเชียบด้านหน้ามา โดย k คือค่าที่ขึ้นกับความหน่วง ยิ่งมากก็ยิ่งทำให้แอมพลิจูดลดลงเร็วขึ้น ในที่นี้ลองให้ k=0.5
ลองเขียนใหม่ โดยคราวนี้เพิ่มตัวสปริงมาด้วย โดยใช้ฟังก์ชัน polyHelix ในการสร้างวัตถุที่เป็นเกลียว
import math
A=10.
f=1.
k=0.5
watthu = mc.polyCube(w=4,h=4,d=4)
spring = mc.polyHelix(c=20,h=20,r=0.1,w=3)
for j in range(1,252):
t = (j-1.)/25
x = math.exp(-k*t)*A*math.cos(2*math.pi*f*t)
mc.setKeyframe(watthu[0],at='ty',v=x,t=j)
mc.setKeyframe(spring[0],at='ty',v=-10+x/2-2,t=j)
mc.setKeyframe(spring[1],at='h',v=20+x,t=j)
A=10.
f=1.
k=0.5
watthu = mc.polyCube(w=4,h=4,d=4)
spring = mc.polyHelix(c=20,h=20,r=0.1,w=3)
for j in range(1,252):
t = (j-1.)/25
x = math.exp(-k*t)*A*math.cos(2*math.pi*f*t)
mc.setKeyframe(watthu[0],at='ty',v=x,t=j)
mc.setKeyframe(spring[0],at='ty',v=-10+x/2-2,t=j)
mc.setKeyframe(spring[1],at='h',v=20+x,t=j)

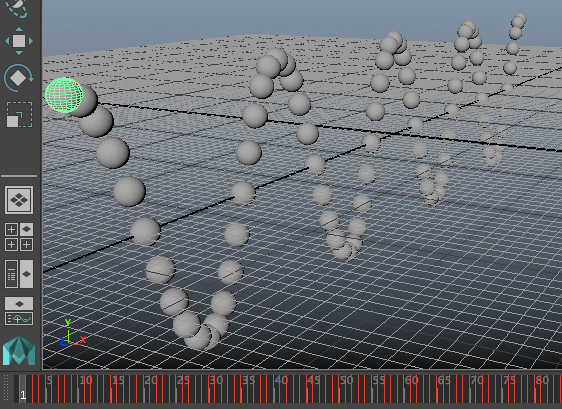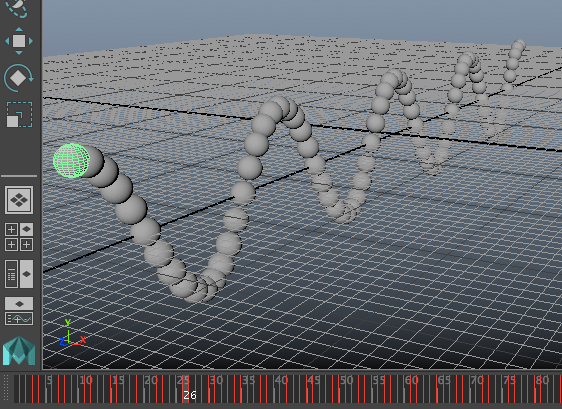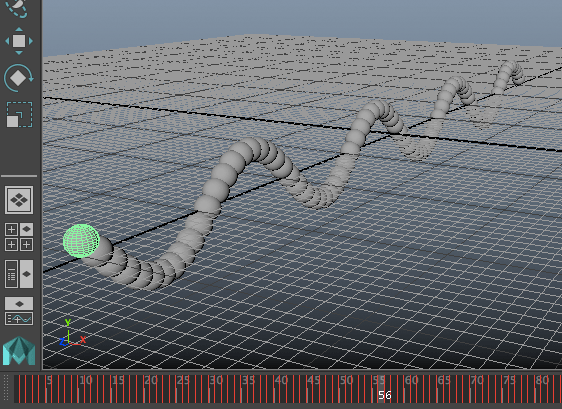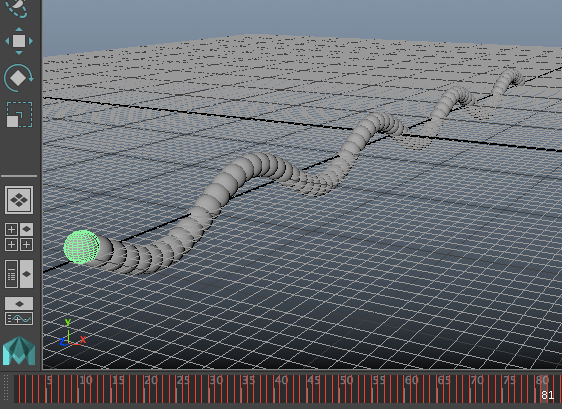
นอกจากนี้ยังอาจลองทำเป็นจำลองคลื่นในเส้นเชือก (คลื่นตามขวาง) โดยให้ทรงกลมหนึ่งลูกแทนมวลในช่วงหนึ่งของเส้นเชือก แล้วสร้างวางเรียงตัวกันไปตามแนวระดับ แต่ละจุดให้มีเฟสเริ่มต้นต่างกัน
import math
A=10.
f=1.
k=0.5
for z in range(-40,41):
chue = mc.polySphere(r=1,n='w%d'%z)
mc.move(0,0,z)
for j in range(1,252):
t = (j-1.)/25
x = math.exp(-k*t)*A*math.cos(2*math.pi*f*(t-z/20.))
mc.setKeyframe(chue[0],at='ty',v=x,t=j)
A=10.
f=1.
k=0.5
for z in range(-40,41):
chue = mc.polySphere(r=1,n='w%d'%z)
mc.move(0,0,z)
for j in range(1,252):
t = (j-1.)/25
x = math.exp(-k*t)*A*math.cos(2*math.pi*f*(t-z/20.))
mc.setKeyframe(chue[0],at='ty',v=x,t=j)

ใน บทนี้เราได้ใช้การทำซ้ำเพื่อตั้งคีย์เฟรมลงบนเส้นเวลาอย่างต่อเนื่อง วิธีการนี้ทำให้เกิดจุดบนคีย์เฟรมมากมายทำให้ดูรกและแก้ไขตอนหลังได้ยาก
ที่ จริงแล้วในกรณีที่มีการเปลี่ยนแปลงเป็นฟังก์ชันที่แน่นอนแบบนี้มีวิธีที่ดี กว่านั้นอยู่ นั่นคือการใช้เอ็กซ์เพรชชัน ซึ่งจะพูดถึงในบทต่อไป
เกี่ยวกับฟังก์ชันอื่นๆเพิ่มเติมในมอดูล math อ่านได้ใน https://phyblas.hinaboshi.com/tsuchinoko16
อ้างอิง