maya python เบื้องต้น บทที่ ๑๕: การทำภาพเคลื่อนไหวด้วยเอ็กซ์เพรชชัน
เขียนเมื่อ 2016/03/10 22:04
แก้ไขล่าสุด 2021/09/28 16:42
ในบทก่อนๆนี้เราได้ทำภาพเคลื่อนไหวโดยใช้ระบบคีย์เฟรม ในบทนี้จะแนะนำอีกวิธีที่ใช้การได้ดีเช่นกัน คือใช้เอ็กซ์เพรชชัน
เอ็กซ์เพรชชัน เป็นวิธีการตั้งให้ค่าองค์ประกอบที่กำหนดเปลี่ยนแปลงไปตามเวลาโดยการกำหนดสมการความสัมพันธ์บางอย่างขึ้น
โดยทั่วไปสามารถกำหนดเอ็กซ์เพรชชันได้โดยเข้าไปที่ expression editor (エクスプレッション エディタ)
เข้าได้โดยดูที่เมนูด้านบน กดที่ Window (ウィンドウ)
ตามด้วย Animation Editors (アニメーション エディタ)
แล้วคลิก Expression Editor (エクスプレッション エディタ)
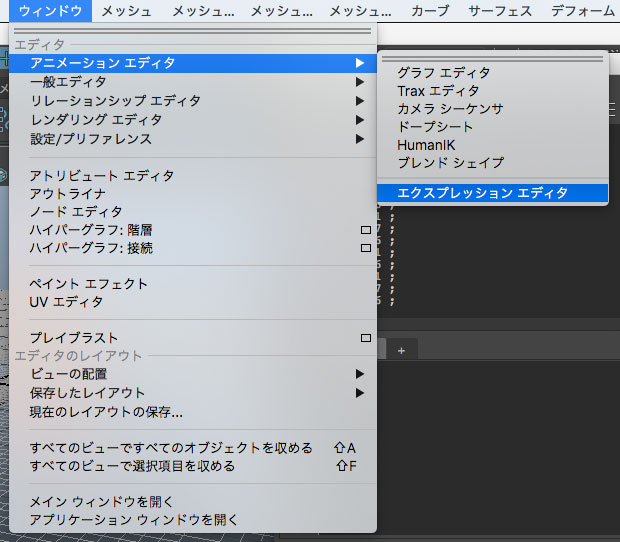
ช่องด้านล่างเป็นที่สำหรับพิมพ์เอ็กซ์เพรชชัน
อย่างไรก็ตาม เราสามารถตั้งเอ็กซ์เพรชชัน ได้โดยไม่ต้องมาเปิดดูหน้าต่างนี้แต่ใช้การเขียนโค้ดไพธอน
วิธีการคือใช้ฟังก์ชัน expression() โดยใส่เอ็กซ์เพรชชันที่ต้องการเขียนไว้ในแฟล็ก s (string)
พิมพ์ mc.expression(s=เอ็กซ์เพรชชันที่ต้องการเขียน)
โค้ดที่ใช้ในการพิมพ์เอ็กซ์เพรชชันนั้นเป็นภาษา MEL ซึ่งเป็นภาษาสั่งการหลักของมายา ไม่สามารถใช้ไพธอนในการเขียนได้
เทียบกับไพธอนแล้ว MEL มีคำสั่งอะไรต่างๆน้อยกว่า ไม่ได้เพียบพร้อมเท่า ดังนั้นอาจใช้งานได้ไม่ยืดหยุ่นเท่าไพธอน
อย่างไรก็ตาม เราสามารถใส่คำสั่งของไพธอนลงไปใน MEL ได้ด้วยการพิมพ์ python("โค้ดไพธอนที่ต้องการ")
วิธีการเขียนอาจมีได้หลากหลาย ขึ้นอยู่กับความสะดวก
โค้ดในภาษา MEL จะคั่นด้วย ; เสมอไม่ว่าจะขึ้นบรรทัดใหม่หรือไม่ ต่างจากไพธอนที่จะคั่นแค่กรณีที่ไม่ขึ้นบรรทัดใหม่ ดังนั้นถ้าไม่ใช่บรรทัดสุดท้ายจะต้องมีเครื่องหมาย ; ปิดท้าย
การประกาศตัวแปรในภาษา MEL นั้นจะต้องใช้ชื่อที่ขึ้นต้นด้วย $ เสมอ ทำให้แยกได้ชัดว่าถ้าเป็น $ ก็คือตัวแปรที่เราประกาศขึ้นใช้เองเพื่อใช้งาน
ในภาษา MEL ไม่ได้มีพวกค่าคงที่เช่นค่า π เตรียมเอาไว้แบบไพธอน จึงต้องกำหนดค่าเอาเอง $pi=3.14159265359
ยกตัวอย่างวิธีการใช้
โดยที่ $A=10; $f=1; $k=0.5; $pi=3.14159265359; คือการประกาศค่าของตัวแปรที่เป็นค่าคงที่
watthu.ty ในที่นี้แทนองค์ประกอบ ty ของวัตถุ ในที่นี้กำหนดให้ค่าเป็นไปตามสมการที่ต้องการ ซึ่งมีค่าแปรเปลี่ยนไปตามเวลา time
time คือเวลาในหน่วยวินาที เป็นตัวแปรพิเศษที่กำหนดใช้ในภาษา MEL ไม่จำเป็นต้องขึ้นต้นด้วย $ นอกจาก time แล้วยังสามารถใช้ frame ซึ่งหมายถึงเวลาในหน่วยเฟรม
บางครั้งอาจเพิ่มแฟล็กไปอีกตัว คือ o (object) คือชื่อของวัตถุ ในกรณีนี้จะพิมพ์แบบนี้
จะเห็นว่าพอกำหนดชื่อวัตถุแล้วภายในสมการจะพิมพ์แค่ ty โดยไม่ต้องใส่ชื่อของวัตถุแล้ว การเขียนแบบนี้อาจสะดวกในกรณีที่ต้องอ้างอิงถึงค่าของวัตถุนี้ในสมการหลาย ครั้ง
ถ้าจะแทนที่ค่า π ด้วยค่าจากฟังก์ชัน math.pi ของไพธอนก็อาจเขียนแบบนี้ python("math.pi")
แต่ค่าที่คืนกลับมาจะเป็นสายอักขระ ต้องใช้ float() เพื่อแปลงเป็นจำนวนจริงที่ต้องการอีกทีเป็น float(python("math.pi")) โดยรวมแล้วอาจเขียนเป็น
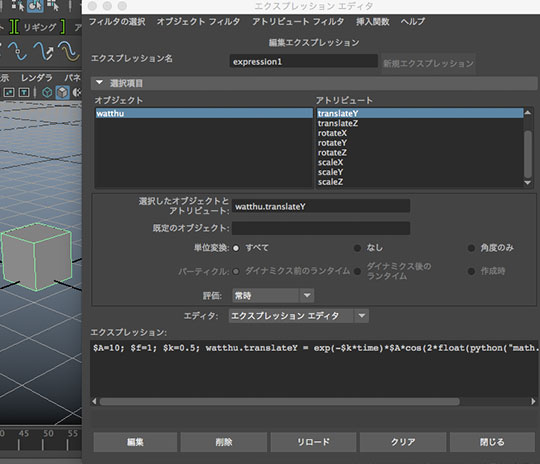
หรือถ้าต้องการประกาศตัวแปรจากในโค้ดไพธอนเลยก็อาจเขียนแบบนี้
ในนี้จะเห็นว่าตัวแปรต่างๆเข้าไปแทนค่า %f ตามลำดับ
ตัวแปรที่ใช้ไม่เพียงแค่ใช้ให้ขึ้นกับเวลา แต่ยังให้ขึ้นกับค่าองค์ประกอบอื่นได้ด้วย เช่นเมื่อเราติดสปริงที่ปลายมวลไปด้วย ก็สามารถใช้ค่า ty ของวัตถุเพื่อกำหนดความยาวของสปริงได้
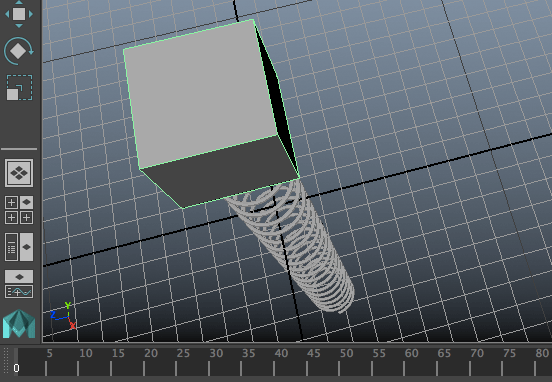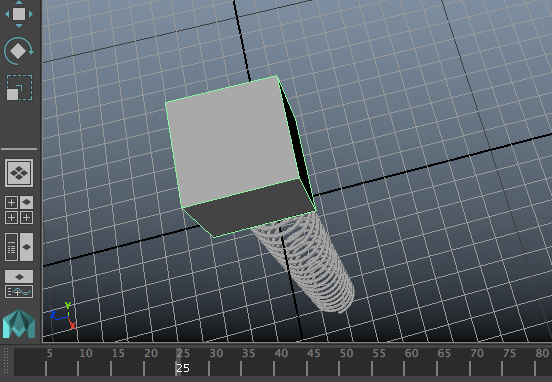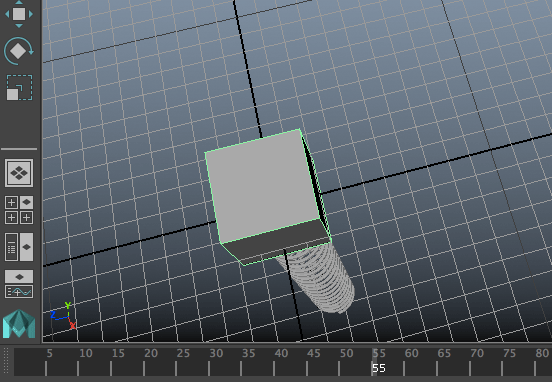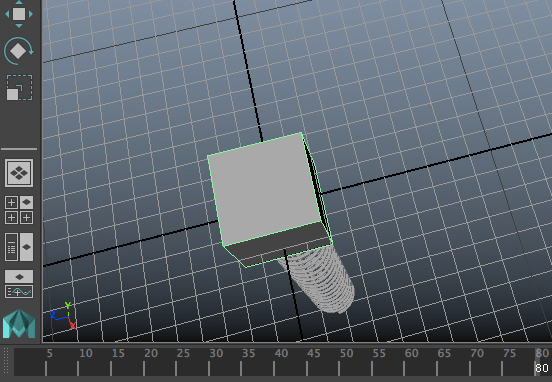
ในตัวอย่างนี้ได้ถือโอกาสเพิ่มแฟล็กอีกตัวหนึ่งลงไปด้วย นั่นคือ n (name) เป็นแฟล็กที่ใช้กำหนดชื่อของเอ็กซ์เพรชชัน เพื่อจะใช้อ้างอิงภายหลัง
ถ้าไม่กำหนดชื่อไว้มันจะถูกตั้งชื่อโดยอัตโนมัติเป็น expression ตามด้วยตัวเลขไปเรื่อยๆตามลำดับ
ฟังก์ชัน expression() สามารถใช้เพื่อดูเอ็กซ์เพรชชันที่ตั้งไปก่อนหน้านี้ได้ด้วย โดยใส่ชื่อของเอ็กซ์เพรชชันที่ต้องการหาค่าเป็นอาร์กิวเมนต์ จากนั้นใส่แฟล็ก q=1,s=1 เช่น
ก็จะได้ค่า
จะเห็นว่าค่าที่ได้คืนกลับมาใช้ชื่อองค์ประกอบเป็นชื่อยาว นั่นเพราะมันถูกเปลี่ยนให้เป็นชื่อยาวโดยอัตโนมัติ แม้ว่าตอนที่เรากำหนดจะใช้ชื่อย่อก็ตาม
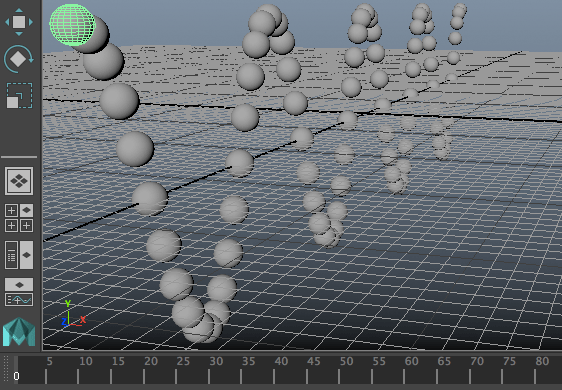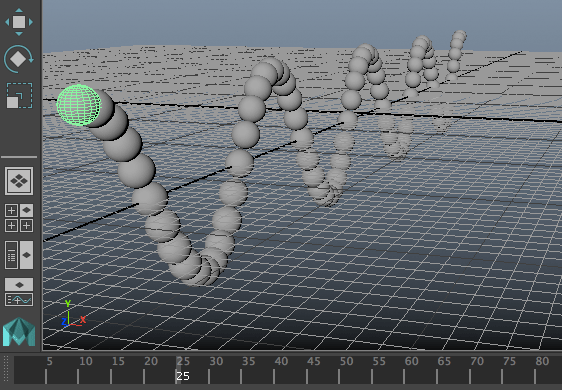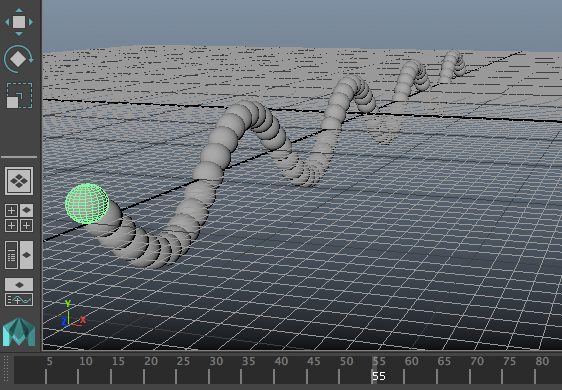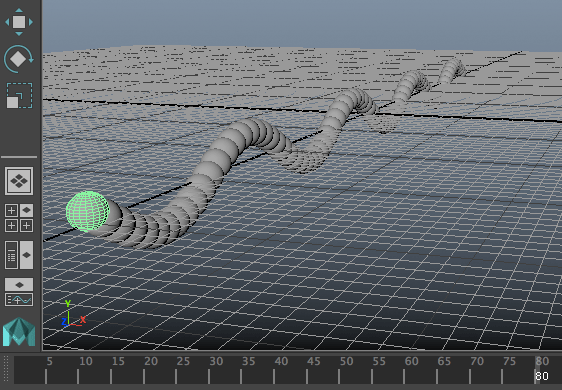
และเช่นเดียวกับบทที่แล้ว วิธีนี้สามารถนำมาใช้สร้างคลื่นในเส้นเชือกได้เหมือนกัน และดูง่ายกว่าด้วย
บางทีการใช้เอ็กซ์เพรชชันก็อาจทำสิ่งที่ไม่เกี่ยวกับเวลาเลยก็เป็นได้ อาจแค่ใช้สร้างความสัมพันธ์ระหว่างค่าองค์ประกอบหนึ่งกับองค์ประกอบอื่น
เช่นในตัวอย่างนี้ สร้างทรงกระบอกที่เรียงตัวกันเป็นเกลียวรูปร่างแปลกๆ

ในนี้จะเห็นว่ากำหนดแค่ tx แต่ให้ไปเป็นตัวกำหนดองค์ประกอบอื่นๆ ได้แก่ความยาวและแกนหมุนของทรงกระบอก
โดยปกติแล้วมักจะใช้เอ็กซ์เพรชชันหนึ่งกำหนดค่าขององค์ประกอบทีละตัวแยกกัน แต่ว่าถ้าอยากกำหนดค่าองค์ประกอบหลายตัวไว้ในเอ็กซ์เพรชชันเดียวกันก็สามารถ ทำได้ เช่นตัวอย่างที่แล้วอาจเขียนใหม่เป็น
แต่เพื่อความเป็นระเบียบ วิธีการเขียนแบบนี้อาจไม่ค่อยน่าแนะนำนัก
จบบทนี้เราได้เรียนรู้วิธีการสร้างภาพเคลื่อนไหวทั้งสองวิธีแล้วทั้งการใช้ คีย์เฟรมและใช้เอ็กซ์เพรชชัน พอมาถึงตรงนี้แล้วก็คงทำให้สามารถสร้างภาพเคลื่อนไหวอะไรต่างๆได้หลากหลาย ตามที่ต้องการ
อ้างอิง
เอ็กซ์เพรชชัน เป็นวิธีการตั้งให้ค่าองค์ประกอบที่กำหนดเปลี่ยนแปลงไปตามเวลาโดยการกำหนดสมการความสัมพันธ์บางอย่างขึ้น
โดยทั่วไปสามารถกำหนดเอ็กซ์เพรชชันได้โดยเข้าไปที่ expression editor (エクスプレッション エディタ)
เข้าได้โดยดูที่เมนูด้านบน กดที่ Window (ウィンドウ)
ตามด้วย Animation Editors (アニメーション エディタ)
แล้วคลิก Expression Editor (エクスプレッション エディタ)

ช่องด้านล่างเป็นที่สำหรับพิมพ์เอ็กซ์เพรชชัน
อย่างไรก็ตาม เราสามารถตั้งเอ็กซ์เพรชชัน ได้โดยไม่ต้องมาเปิดดูหน้าต่างนี้แต่ใช้การเขียนโค้ดไพธอน
วิธีการคือใช้ฟังก์ชัน expression() โดยใส่เอ็กซ์เพรชชันที่ต้องการเขียนไว้ในแฟล็ก s (string)
พิมพ์ mc.expression(s=เอ็กซ์เพรชชันที่ต้องการเขียน)
โค้ดที่ใช้ในการพิมพ์เอ็กซ์เพรชชันนั้นเป็นภาษา MEL ซึ่งเป็นภาษาสั่งการหลักของมายา ไม่สามารถใช้ไพธอนในการเขียนได้
เทียบกับไพธอนแล้ว MEL มีคำสั่งอะไรต่างๆน้อยกว่า ไม่ได้เพียบพร้อมเท่า ดังนั้นอาจใช้งานได้ไม่ยืดหยุ่นเท่าไพธอน
อย่างไรก็ตาม เราสามารถใส่คำสั่งของไพธอนลงไปใน MEL ได้ด้วยการพิมพ์ python("โค้ดไพธอนที่ต้องการ")
วิธีการเขียนอาจมีได้หลากหลาย ขึ้นอยู่กับความสะดวก
โค้ดในภาษา MEL จะคั่นด้วย ; เสมอไม่ว่าจะขึ้นบรรทัดใหม่หรือไม่ ต่างจากไพธอนที่จะคั่นแค่กรณีที่ไม่ขึ้นบรรทัดใหม่ ดังนั้นถ้าไม่ใช่บรรทัดสุดท้ายจะต้องมีเครื่องหมาย ; ปิดท้าย
การประกาศตัวแปรในภาษา MEL นั้นจะต้องใช้ชื่อที่ขึ้นต้นด้วย $ เสมอ ทำให้แยกได้ชัดว่าถ้าเป็น $ ก็คือตัวแปรที่เราประกาศขึ้นใช้เองเพื่อใช้งาน
ในภาษา MEL ไม่ได้มีพวกค่าคงที่เช่นค่า π เตรียมเอาไว้แบบไพธอน จึงต้องกำหนดค่าเอาเอง $pi=3.14159265359
ยกตัวอย่างวิธีการใช้
mc.polyCube(n='watthu')
mc.expression(s='$A=10; $f=1; $k=0.5; $pi=3.14159265359; watthu.ty = exp(-$k*time)*$A*cos(2*$pi*$f*time);')
mc.expression(s='$A=10; $f=1; $k=0.5; $pi=3.14159265359; watthu.ty = exp(-$k*time)*$A*cos(2*$pi*$f*time);')
โดยที่ $A=10; $f=1; $k=0.5; $pi=3.14159265359; คือการประกาศค่าของตัวแปรที่เป็นค่าคงที่
watthu.ty ในที่นี้แทนองค์ประกอบ ty ของวัตถุ ในที่นี้กำหนดให้ค่าเป็นไปตามสมการที่ต้องการ ซึ่งมีค่าแปรเปลี่ยนไปตามเวลา time
time คือเวลาในหน่วยวินาที เป็นตัวแปรพิเศษที่กำหนดใช้ในภาษา MEL ไม่จำเป็นต้องขึ้นต้นด้วย $ นอกจาก time แล้วยังสามารถใช้ frame ซึ่งหมายถึงเวลาในหน่วยเฟรม
บางครั้งอาจเพิ่มแฟล็กไปอีกตัว คือ o (object) คือชื่อของวัตถุ ในกรณีนี้จะพิมพ์แบบนี้
mc.polyCube(n='watthu')
mc.expression(o='watthu',s='$A=10; $f=1; $k=0.5; $pi=3.14159265359; ty = exp(-$k*time)*$A*cos(2*$pi*$f*time);')
mc.expression(o='watthu',s='$A=10; $f=1; $k=0.5; $pi=3.14159265359; ty = exp(-$k*time)*$A*cos(2*$pi*$f*time);')
จะเห็นว่าพอกำหนดชื่อวัตถุแล้วภายในสมการจะพิมพ์แค่ ty โดยไม่ต้องใส่ชื่อของวัตถุแล้ว การเขียนแบบนี้อาจสะดวกในกรณีที่ต้องอ้างอิงถึงค่าของวัตถุนี้ในสมการหลาย ครั้ง
ถ้าจะแทนที่ค่า π ด้วยค่าจากฟังก์ชัน math.pi ของไพธอนก็อาจเขียนแบบนี้ python("math.pi")
แต่ค่าที่คืนกลับมาจะเป็นสายอักขระ ต้องใช้ float() เพื่อแปลงเป็นจำนวนจริงที่ต้องการอีกทีเป็น float(python("math.pi")) โดยรวมแล้วอาจเขียนเป็น
import math
mc.polyCube(n='watthu')
mc.expression(s='$A=10; $f=1; $k=0.5; watthu.ty = exp(-$k*time)*$A*cos(2*float(python("math.pi"))*$f*time);')
mc.polyCube(n='watthu')
mc.expression(s='$A=10; $f=1; $k=0.5; watthu.ty = exp(-$k*time)*$A*cos(2*float(python("math.pi"))*$f*time);')

หรือถ้าต้องการประกาศตัวแปรจากในโค้ดไพธอนเลยก็อาจเขียนแบบนี้
import math
watthu = mc.polyCube()
A=10
f=1
k=0.5
mc.expression(o=watthu[0],s='ty = exp(-%f*time)*%f*cos(2*%f*%f*time);'%(k,A,math.pi,f))
watthu = mc.polyCube()
A=10
f=1
k=0.5
mc.expression(o=watthu[0],s='ty = exp(-%f*time)*%f*cos(2*%f*%f*time);'%(k,A,math.pi,f))
ในนี้จะเห็นว่าตัวแปรต่างๆเข้าไปแทนค่า %f ตามลำดับ
ตัวแปรที่ใช้ไม่เพียงแค่ใช้ให้ขึ้นกับเวลา แต่ยังให้ขึ้นกับค่าองค์ประกอบอื่นได้ด้วย เช่นเมื่อเราติดสปริงที่ปลายมวลไปด้วย ก็สามารถใช้ค่า ty ของวัตถุเพื่อกำหนดความยาวของสปริงได้
import math
watthu = mc.polyCube(w=4,h=4,d=4)
spring = mc.polyHelix(c=20,h=20,r=0.1,w=3)
A=10
f=1
k=0.5
mc.expression(s=watthu[0]+'.ty = exp(-%f*time)*%f*cos(2*%f*%f*time);'%(k,A,math.pi,f),n='watthu_ty')
mc.expression(s=spring[1]+'.h = 20+'+watthu[0]+'.ty',n='spring_h')
mc.expression(s=spring[0]+'.ty = -10+'+watthu[0]+'.ty/2-2',n='spring_ty')
watthu = mc.polyCube(w=4,h=4,d=4)
spring = mc.polyHelix(c=20,h=20,r=0.1,w=3)
A=10
f=1
k=0.5
mc.expression(s=watthu[0]+'.ty = exp(-%f*time)*%f*cos(2*%f*%f*time);'%(k,A,math.pi,f),n='watthu_ty')
mc.expression(s=spring[1]+'.h = 20+'+watthu[0]+'.ty',n='spring_h')
mc.expression(s=spring[0]+'.ty = -10+'+watthu[0]+'.ty/2-2',n='spring_ty')

ในตัวอย่างนี้ได้ถือโอกาสเพิ่มแฟล็กอีกตัวหนึ่งลงไปด้วย นั่นคือ n (name) เป็นแฟล็กที่ใช้กำหนดชื่อของเอ็กซ์เพรชชัน เพื่อจะใช้อ้างอิงภายหลัง
ถ้าไม่กำหนดชื่อไว้มันจะถูกตั้งชื่อโดยอัตโนมัติเป็น expression ตามด้วยตัวเลขไปเรื่อยๆตามลำดับ
ฟังก์ชัน expression() สามารถใช้เพื่อดูเอ็กซ์เพรชชันที่ตั้งไปก่อนหน้านี้ได้ด้วย โดยใส่ชื่อของเอ็กซ์เพรชชันที่ต้องการหาค่าเป็นอาร์กิวเมนต์ จากนั้นใส่แฟล็ก q=1,s=1 เช่น
print(mc.expression('spring_h',q=1,s=1))
ก็จะได้ค่า
polyHelix1.height = 20+pCube1.translateY
จะเห็นว่าค่าที่ได้คืนกลับมาใช้ชื่อองค์ประกอบเป็นชื่อยาว นั่นเพราะมันถูกเปลี่ยนให้เป็นชื่อยาวโดยอัตโนมัติ แม้ว่าตอนที่เรากำหนดจะใช้ชื่อย่อก็ตาม
และเช่นเดียวกับบทที่แล้ว วิธีนี้สามารถนำมาใช้สร้างคลื่นในเส้นเชือกได้เหมือนกัน และดูง่ายกว่าด้วย
import math
A=10.
f=1.
k=0.5
for z in range(-40,41):
chue = mc.polySphere(r=1,n='w%d'%z)
mc.move(0,0,z)
mc.expression(o=chue[0],s='ty = exp(-%f*time)*%f*cos(2*%f*%f*(time-tz/20));'%(k,A,math.pi,f))
A=10.
f=1.
k=0.5
for z in range(-40,41):
chue = mc.polySphere(r=1,n='w%d'%z)
mc.move(0,0,z)
mc.expression(o=chue[0],s='ty = exp(-%f*time)*%f*cos(2*%f*%f*(time-tz/20));'%(k,A,math.pi,f))

บางทีการใช้เอ็กซ์เพรชชันก็อาจทำสิ่งที่ไม่เกี่ยวกับเวลาเลยก็เป็นได้ อาจแค่ใช้สร้างความสัมพันธ์ระหว่างค่าองค์ประกอบหนึ่งกับองค์ประกอบอื่น
เช่นในตัวอย่างนี้ สร้างทรงกระบอกที่เรียงตัวกันเป็นเกลียวรูปร่างแปลกๆ
for i in range(160):
watthu = mc.polyCylinder(r=1)
mc.move(i,0,0)
mc.expression(o=watthu[0],s='ty = 25*pow(cos(tx/10),2)')
mc.expression(o=watthu[1],s='h = 50*pow(cos('+watthu[0]+'.tx/10),2)')
mc.expression(o=watthu[1],s='axy = 4*sin('+watthu[0]+'.tx/4)')
mc.expression(o=watthu[1],s='axz = 4*cos('+watthu[0]+'.tx/4)')
watthu = mc.polyCylinder(r=1)
mc.move(i,0,0)
mc.expression(o=watthu[0],s='ty = 25*pow(cos(tx/10),2)')
mc.expression(o=watthu[1],s='h = 50*pow(cos('+watthu[0]+'.tx/10),2)')
mc.expression(o=watthu[1],s='axy = 4*sin('+watthu[0]+'.tx/4)')
mc.expression(o=watthu[1],s='axz = 4*cos('+watthu[0]+'.tx/4)')

ในนี้จะเห็นว่ากำหนดแค่ tx แต่ให้ไปเป็นตัวกำหนดองค์ประกอบอื่นๆ ได้แก่ความยาวและแกนหมุนของทรงกระบอก
โดยปกติแล้วมักจะใช้เอ็กซ์เพรชชันหนึ่งกำหนดค่าขององค์ประกอบทีละตัวแยกกัน แต่ว่าถ้าอยากกำหนดค่าองค์ประกอบหลายตัวไว้ในเอ็กซ์เพรชชันเดียวกันก็สามารถ ทำได้ เช่นตัวอย่างที่แล้วอาจเขียนใหม่เป็น
for i in range(160):
watthu = mc.polyCylinder(r=1)
mc.move(i,0,0)
mc.expression(s=watthu[0]+'.ty = 25*pow(cos('+watthu[0]+'.tx/10),2); '
+watthu[1]+'.h = 50*pow(cos('+watthu[0]+'.tx/10),2); '
+watthu[1]+'.axy = 4*sin('+watthu[0]+'.tx/4); '
+watthu[1]+'.axz = 4*cos('+watthu[0]+'.tx/4)')
watthu = mc.polyCylinder(r=1)
mc.move(i,0,0)
mc.expression(s=watthu[0]+'.ty = 25*pow(cos('+watthu[0]+'.tx/10),2); '
+watthu[1]+'.h = 50*pow(cos('+watthu[0]+'.tx/10),2); '
+watthu[1]+'.axy = 4*sin('+watthu[0]+'.tx/4); '
+watthu[1]+'.axz = 4*cos('+watthu[0]+'.tx/4)')
แต่เพื่อความเป็นระเบียบ วิธีการเขียนแบบนี้อาจไม่ค่อยน่าแนะนำนัก
จบบทนี้เราได้เรียนรู้วิธีการสร้างภาพเคลื่อนไหวทั้งสองวิธีแล้วทั้งการใช้ คีย์เฟรมและใช้เอ็กซ์เพรชชัน พอมาถึงตรงนี้แล้วก็คงทำให้สามารถสร้างภาพเคลื่อนไหวอะไรต่างๆได้หลากหลาย ตามที่ต้องการ
อ้างอิง
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/expression.html
http://help.autodesk.com/view/MAYAUL/2016/JPN/?guid=GUID-EF3F2007-74E7-4F23-B4A3-8D2EF94579A1
https://knowledge.autodesk.com/ja/support/maya/learn-explore/caas/CloudHelp/cloudhelp/2016/JPN/Maya/files/GUID-251640EA-AACC-4F1B-A341-297F0F4CEFE4-htm.html
http://tommy-on.hatenablog.com/entry/2015/07/09/093904
http://www.not-enough.org/abe/manual/maya-python-aa07/expression.html
http://help.autodesk.com/view/MAYAUL/2016/JPN/?guid=GUID-EF3F2007-74E7-4F23-B4A3-8D2EF94579A1
https://knowledge.autodesk.com/ja/support/maya/learn-explore/caas/CloudHelp/cloudhelp/2016/JPN/Maya/files/GUID-251640EA-AACC-4F1B-A341-297F0F4CEFE4-htm.html
http://tommy-on.hatenablog.com/entry/2015/07/09/093904
http://www.not-enough.org/abe/manual/maya-python-aa07/expression.html