ในบทที่ ๑๘ ได้พูดถึงการรวมโพลิกอนเป็นกลุ่มไปแล้ว แต่การรวมเป็นกลุ่มแบบนั้นเป็นแค่การรวมกันแบบหลวมๆ ในบทนี้จะแนะนำการรวมโพลิกอนหลายชิ้นเป็นโพลิกอนชิ้นเดียวกัน

คำสั่งที่ใช้รวมโพลิกอนคือฟังก์ชัน polyUnite() โดยใส่วัตถุโพลิกอนที่ต้องการรวมทั้งหมดเป็นอาร์กิวเมนต์ จากนั้นวัตถุจะรวมกันโดยเกิดเป็นวัตถุใหม่ขึ้นมา สามารถตั้งชื่อวัตถุใหม่ที่เกิดขึ้นได้

ตัวอย่าง ลองสร้างทรงกลมหลายๆอันมาเรียงซ้อนกันจนรูปร่างคล้ายครัวซ็องแล้วนำมารวมเป็นโพลิกอนเดียวกัน


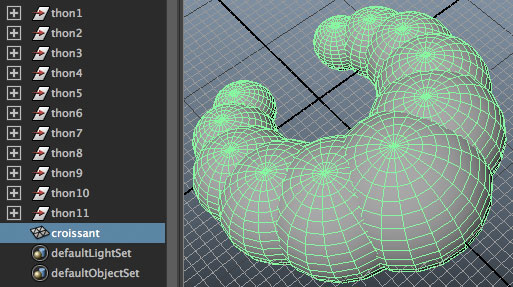
เมื่อใช้คำสั่งนี้รวมวัตถุไปแล้ว พอไปดูที่ outliner จะเห็นว่าวัตถุเดิมกลายมาเป็นโหนดใหม่ซึ่งเมื่อเปิดเข้าไปดูจะเห็นโหนดที่ ชื่อขึ้นต้นด้วย transform ในนั้นจะเก็บค่ารูปร่างของวัตถุตั้งแต่ก่อนที่มันจะมารวมกันไว้ทั้งหมด สามารถปรับแก้จากตรงนี้เพื่อให้วัตถุมีการเปลี่ยนแปลงได้ไม่ต่างจากตอนก่อน ที่จะรวม

เวลาคลิกเลือกวัตถุที่หน้าจอโดยตรงไม่ว่าจะคลิกตรงส่วนไหน ก็จะกลายเป็นการเลือกทั้งหมดไป หากจะควบคุมแยกส่วนก็ต้องไปกดที่โหนดใน outliner เอาเท่านั้น

หากปล่อยโหนดเอาไว้เช่นนี้ outliner จะดูรก หากคิดว่าไม่จำเป็นจำต้องกลับไปแก้แต่ละส่วนแบบแยกกันอีกแล้วก็สามารถลบโหนดนี้ทิ้งได้ตอนที่รวม โดยเพิ่มแฟล็ก ch (constructionHistory) เป็น ch=0 วัตถุที่รวมก็จะกลายเป็นชิ้นเดียวกันโดยไม่เหลือประวัติศาสตร์เดิมตอนก่อน แยก

แต่ก็ไม่ใช่ว่าวัตถุจะรวมกันโดยสมบูรณ์จนแยกไม่ออกแล้ว จะเห็นว่ามันยังดูเหมือนแยกกันเป็นสองชิ้นอยู่ดี หากไม่มีจุดยอดสักจุดเชื่อมต่อกันแม้จะอยู่ในโพลิกอนเดียวกันแต่ก็ยังถือว่า อยู่กันคนละเชล

เชล (シェル, shell) หมายถึงชิ้นของโพลิกอน กลุ่มของหน้าโพลิกอนที่มีจุดหรือเส้นขอบติดกันจะเรียกว่าเป็นเชลเดียวกัน แต่ถ้าไม่มีการเชือมต่อกันเลยจะถือว่าเป็นคนละเชล

การหาจำนวนเชลสามารถใช้ฟังก์ชัน polyEvaluate() โดยใส่แฟล็ก s (shell)
พื้นผิวต่อให้ซ้อนทับกันก็ไม่ถือว่าเป็นเชลเดียวกัน หรือแม้แต่ต่อให้มีจุดซ้อนทับในตำแหน่งเดียวกันก็ยังไม่ถือว่าเป็นเชล เดียวกันอยู่ดี เพราะยังถือว่าเป็นจุดสองจุด แม้จะทับกันก็ตาม

แต่หากนำจุดนั้นมาหลอมรวมเป็นจุดเดียวกันแล้วมันก็จะกลายเป็นเชลเดียวกันทันที

การหลอมรวมจุดที่ซ้อนทับกันสามารถทำได้โดยใช้ฟังก์ชัน polyMergeVertex() โดยใส่แฟล็กที่ต้องใส่คือ d (distance) คือระยะสูงสุดของจุดที่ต้องการให้หลมรวมกัน จะกำหนดแคบแค่ไหนก็ได้ แต่ต้องให้แคบพอที่จะไม่กระทบต่อจุดยอดที่แค่อยู่ใกล้กันมากแต่ไม่ได้ตั้งใจจะรวม

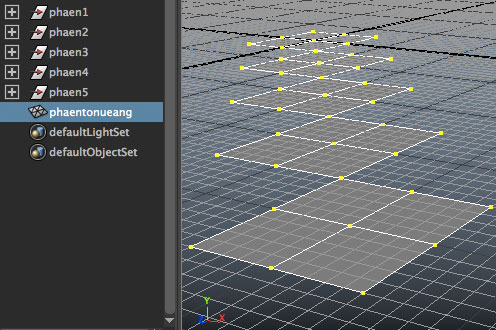
หลังจากที่หลอมรวมกันแล้วก็จะพบว่าจำนวนเชลลดลง เช่นตัวอย่างนี้ ลองหาจำนวนเชลก่อนรวมกับหลังรวม


หากต้องการแยกเชลออกเป็นโพลิกอนคนละชิ้นกันก็สามารถทำได้โดยใช้ฟังก์ชัน polySeparate() แต่ละเชลจะถูกแยกออกมาเป็นส่วนๆโดยยังถูกรวมอยู่ในกลุ่มเดียวกัน

ลองสร้างโพลิกอนแบบตัวอย่างที่แล้วอีกทีเสร็จแล้วก็รวมกันโดยไม่ใช้ polyMergeVertex() เสร็จแล้วก็แยกกันกลับออกมาทันที


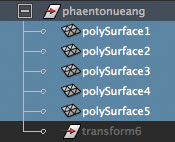
ชื่อวัตถุตอนที่รวมจะกลายมาเป็นชื่อกลุ่ม ส่วนแผ่นที่แยกออกมาจะไม่ได้คืนชื่อเดิมแต่จะถูกตั้งชื่อใหม่ให้อัตโนมัติ แต่ก็สามารถตั้งชื่อใหม่ได้โดยเติมแฟล็ก n (name)



อ้างอิง

<< บทที่แล้ว      บทถัดไป >>
หน้าสารบัญ

~ 自己紹介 ~

目次

日本による名言集

python モジュール -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 機械学習 -- ニューラル      ネットワーク

javascript

モンゴル語

言語学

maya

確率論

日本での日記

中国での日記 -- 北京での日記 -- 香港での日記 -- 澳門での日記

台灣での日記

北欧での日記

他の国での日記

qiita

その他の記事

記事の類別

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --MATLAB --SQL --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม --สเตเบิลดิฟฟิวชัน ---comfyui -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ -ซางะ -นางาซากิ -คุมาโมโตะ -โออิตะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ -ออสเตรเลีย ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -ภูเขาไฟ -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม เรื่องแต่ง บันทึก

　 記事を検索

　 最新記事

　 おすすめの記事

月別記事

もっと前の記事

ไทย

日本語

中文