การแปลงจากส่วนกลับของความน่าจะเป็นสะสม

บทความนี้จะพูดถึงเรื่องของการสุ่มตัวอย่างโดยการแปลงผกผัน (逆变换采样, inverse transform sampling) ซึ่งเป็นวิธีหนึ่งที่ใช้มากในการสร้างค่าสุ่ม

ก่อนหน้านี้ได้เขียนถึงวิธีการสุ่มตัวอย่างที่เรียบง่ายแต่ประสิทธิภาพต่ำไปแล้ว นั่นคือ การด้วยการคัดเอาหรือคัดทิ้ง

สำหรับวิธีการที่จะกล่าวถึงในบทนี้คือการสุ่มตัวอย่างโดยการใช้ค่านั่นคือสิ่งที่เรียกว่าฟังก์ชันจุดร้อยละ (percent point function หรือต่อจากนี้จะเรียกย่อๆว่า PPF) ซึ่งเป็นการค่าส่วนกลับของฟังก์ชันแจกแจงสะสม (cumulative distribution function) ของการแจกแจงนั้นๆ

ถ้าใช้ scipy.stats ฟังก์ชัน PPF นี้ก็คำนวณได้โดยเมธอด .ppf() นั่นเอง

เมื่อใช้วิธีนี้สามารถแปลงผลการสุ่มจากแบบเอกรูปให้เป็นแบบที่ต้องการได้ หลักการไม่ได้ซับซ้อนมาก แต่มีส่วนที่ชวนให้สับสนได้ง่าย

ข้อดีของวิธีนี้คือจะไม่มีการทิ้งค่าที่สุ่มไปแม้แต่ตัวเดียว ทุกค่าที่สุ่มขึ้นมาจะถูกแปลงค่าเพื่อให้เข้ากับการแจกแจงที่ต้องการและได้ใช้ทั้งหมด




การสุ่มค่าแบบไม่ต่อเนื่อง

การสุ่มตัวอย่างโดยการแปลงผกผันนั้นในทางปฏิบัติแล้วจะใช้กับการสุ่มค่าแบบต่อเนื่องมากกว่า แต่เพื่อให้เข้าใจที่มาที่ไปของวิธีนี้จึงขอเริ่มจากอธิบายโดยยกตัวอย่างการสุ่มค่าแบบต่อเนื่อง ซึ่งค่อนข้างเข้าใจง่ายเห็นภาพได้ชัดกว่าก่อน

สมมุติว่ามีค่าที่ต้องการสุ่มให้แจกแจงตามนี้


นี่เป็นตัวอย่างฟังก์ชันการแจกแจงแบบต่อเนื่อง โดยให้มีค่าเฉพาะเมื่อ x เป็นจำนวนเต็มบวก

ลองเขียนโค้ดแสดงกราฟของฟังก์ชัน ก็จะได้แบบนี้

def f(x):
    return (5/6)**(x-1)-(5/6)**x

x = np.arange(1,20+1)
P = f(x)
plt.xlabel('x')
plt.ylabel('P(X=x)')
plt.title('การแจกแจงความน่าจะเป็น',family='Tahoma')
plt.plot(x,P,'mo-')
plt.show()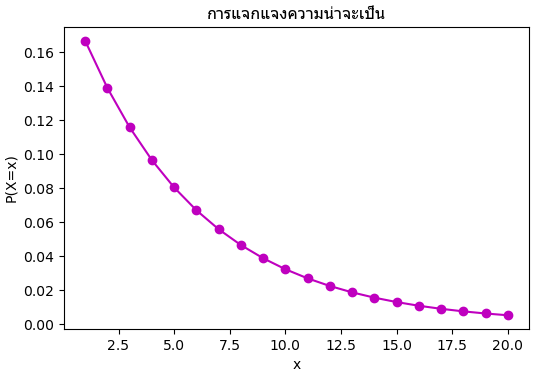

ลักษณะการแจกแจงจะสูงสุดที่ x=1 แล้วค่อยๆลดลงเมื่อ x มากขึ้น จนเข้าใกล้ 0 ที่อนันต์

สิ่งที่จะพิจารณาในที่นี้คือฟังก์ชันแจกแจงสะสม คือความน่าจะเป็นสะสมรวมตั้งแต่ x=1 ไปจนถึงค่าที่พิจารณา


ลองวาดโค้ดแสดงความน่าจะเป็นสะสม โดยไล่ตั้งแต่ x=1 ได้ดังนี้

plt.xlabel('x')
plt.ylabel('$F_X(x)$')
plt.title('ความน่าจะเป็นสะสมรวม',family='Tahoma')
Pcum = 0
for x in range(1,20):
    Pcum += f(x) # คำนวณฟังก์ชันความน่าจะเป็นแล้วบวกสะสมไปในแต่ละขั้น
    c = np.random.random(3) # สุ่มสี
    plt.plot([21,x],[Pcum,Pcum],'--',c=c)
    plt.text(x,Pcum,x,va='top',c=c)
plt.show()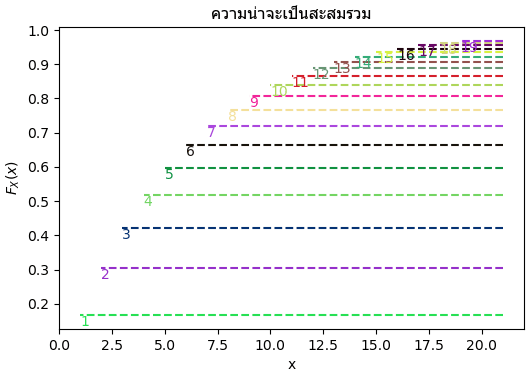

ฟังก์ชันการแจกแจงสะสมเป็นบวกเสมอ โดยค่าไล่ตั้งแต่ 0 ถึง 1 ในที่นี้จึงได้ลองวาดให้เห็นเป็นขั้นๆดู เมื่อลองมองภาพตามนี้แล้วจะเห็นว่าแต่ละตัวเลขนั้นแบ่งช่วงกันอย่างชัดเจนภายในค่า 0 ถึง 1

เมื่อเห็นแบบนี้แล้วก็ชวนให้นึกออกได้ว่า ถ้าหากเราทำการสุ่มค่าตั้งแต่ 0 ถึง 1 แล้วดูว่าค่าอยู่ในช่วงของเลขไหน เราก็จะได้การแจกแจงเป็นไปตามนี้นั่นเอง เพราะช่วงยิ่งกว้างยิ่งหมายถึงว่าความน่าจะเป็นมาก

ลองเขียนโค้ดแสดงการสุ่มด้วยวิธีดังที่ว่านี้ดู

x = [] # สุ่มดูสักหมื่นตัว
for i in range(10000):
    ycum = 0 # ความน่าจะเป็นสะสม
    xi = 0
    u = random.random() # สุ่มค่าในช่วง 0 ถึง 1
    # ไล่เทียบดูทีละขั้นว่าค่าที่สุ่มได้อยู่ในช่วงไหน
    while(u>ycum):
        xi = xi+1
        ycum = ycum+f(xi)
    # ถ้า u มากกว่าความน่าจะเป็นสะสมก็หยุดแล้วเก็บค่านั้น
    x.append(xi)

bx = np.bincount(x) # นับค่าว่ามีเลขไหนกี่ตัว
plt.xlabel('x')
plt.bar(range(len(bx)),bx,fc='m',ec='k')
plt.show()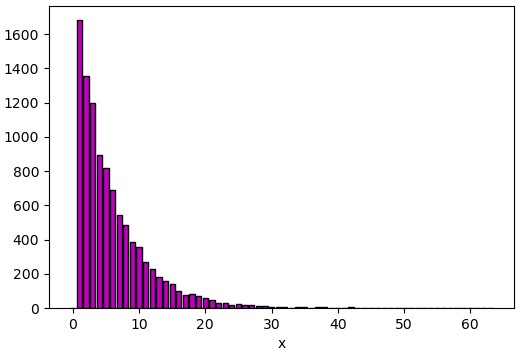

ดูผลแล้วจะเห็นว่าการแจกแจงที่ได้เป็นไปตามฟังก์ชันการแจกแจงข้างต้นจริงๆ

การพิจารณาความน่าจะเป็นสะสมแบบนี้ก็คือวิธีการที่เรียกว่าการสุ่มตัวอย่างโดยการแปลงผกผัน คือเหมือนเป็นการคิดย้อนกลับ

ที่เรียกว่า "ผกผัน" เพราะจริงๆแล้วสิ่งที่ถูกพิจารณาจริงๆไม่ใช่ตัวความน่าจะเป็นสะสมโดยตรง แต่เป็นส่วนกลับของมัน ซึ่งก็คือ PPF ดังที่ได้กล่าวไปข้างต้น

อาจลองวาดกราฟ PPF ดูได้ดังนี้ โค้ดคล้ายกับตอนสร้างค่าสุ่มแจกแจง แต่คราวนี้ให้เป็นค่าไล่ไปเรื่อยๆตั้งแต่ 0 ถึง 1 โดยแบ่งเป็นพันช่วง

q = np.linspace(0,1,1001)[:-1]
x = []
for u in q:
    ycum = 0
    xi = 0
    while(u>ycum):
        xi += 1
        ycum += f(xi)
    x.append(xi)

plt.xlabel('$F_X(x)$')
plt.ylabel('x')
plt.plot(q,x,'m')
plt.show()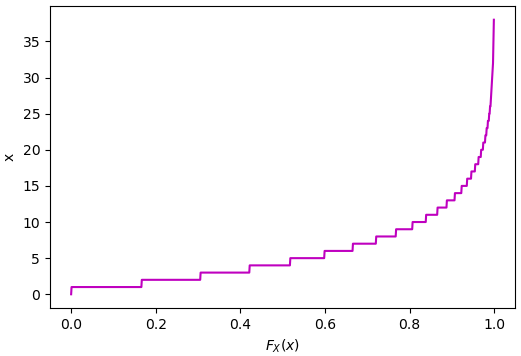

เนื่องจากเป็นการแจกแจงแบบไม่ต่อเนื่อง กราฟ PPF ก็จะเป็นขั้นบันไดแบบนี้

จะเห็นว่าถ้าเราสุ่มค่าตั้งแต่ 0 ถึง 1 แล้วคำนวณ PPF ค่าที่ได้ก็จะเป็นการแจกแจงตามที่ต้องการ

หลักการนี้สามารถใช้กับการแจกแจงที่เป็นค่าแบบต่อเนื่องได้เช่นกัน




การสุ่มค่าแบบต่อเนื่อง

เมื่อเข้าใจหลักการโดยรวมของวิธีการสุ่มตัวอย่างโดยการแปลงผกผันจากกรณีของค่าแบบไม่ต่อเนื่องแล้ว คราวนี้ลองพิจารณาค่าต่อเนื่อง ซึ่งก็ใช้หลักการเดียวกัน แต่จริงๆแล้วคำนวณได้ง่ายกว่า และใช้งานได้จริงในทางปฏิบัติมากกว่า

เพื่อความง่าย พิจารณาการแจกแจงแบบง่ายๆ คือการแจกแจงแบบเลขชี้กำลังที่ λ=1 ซึ่งมีฟังก์ชันการแจกแจงความหนาแน่นของความน่าจะเป็นดังนี้


วาดกราฟดูได้ดังนี้

def f(x):
    return np.exp(-x)

x = np.linspace(0,4,101)
P = f(x)
plt.xlabel('x')
plt.ylabel('$f_X(x)$')
plt.title('การแจกแจงความหนาแน่นความน่าจะเป็น',family='Tahoma')
plt.plot(x,P,'g')
plt.show()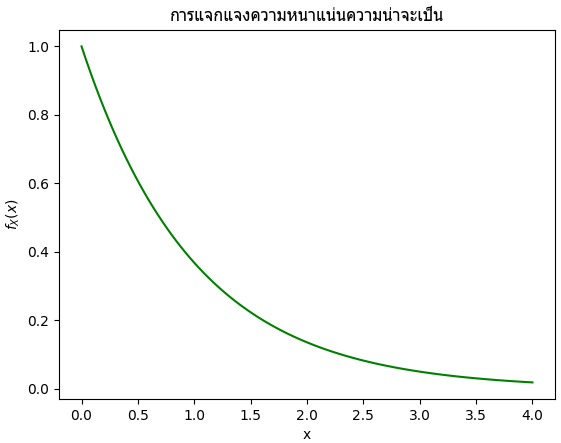

ส่วนฟังก์ชันความน่าจะเป็นสะสมก็จะคำนวณได้จากการหาปริพันธ์ นั่นคือ


ลองวาดค่าของฟังก์ชันความหนาแน่นสะสมเป็นขั้นๆดู แต่ครั้งนี้ต่างจากกรณีค่าไม่ต่อเนื่อง ตรงที่ว่าไม่ได้มีการแบ่งช่วงที่แน่นอน ดังนั้นเส้นที่วาดในที่นี้จึงเป็นแค่เส้นแสดงตำแหน่ง

def pdf(x):
    return 1-np.exp(-x)

plt.xlabel('x')
plt.ylabel('$F_X(x)$')
plt.title('ความน่าจะเป็นสะสมรวม',family='Tahoma')
Pcum = P.cumsum()
for x in np.arange(0.4,4,0.4):
    c = np.random.random(3)
    pdfx = pdf(x)
    plt.plot([5,x],[pdfx,pdfx],'--',c=c)
    plt.text(x,pdfx,'%.2f'%x,va='top',c=c)
plt.show()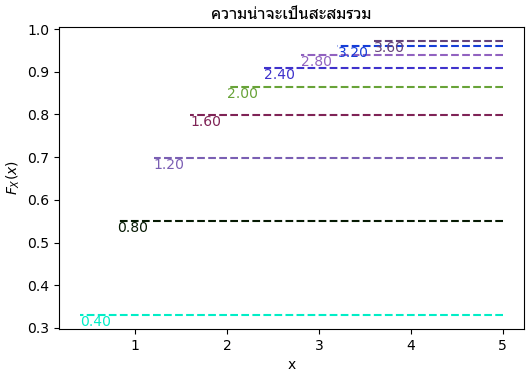

จากตรงนี้จะเห็นได้ว่าหากสุ่มค่าตั้งแต่ 0 ถึง 1 แล้วเทียบดูว่าตำแหน่งนั้นเป็นความน่าจะเป็นสะสมรวมของที่ค่า x เป็นเท่าใด ก็จะได้ค่า x ที่เป็นการแจกแจงตามที่ต้องการ

ซึ่งอาจลองทำดูได้เช่นเดียวกับที่ทำกับการแจกแจงแบบไม่ต่อเนื่อง โดยเขียนแบบนี้

x = []
for i in range(10000):
    u = random.random()
    xi = 0
    while(u>pdf(xi)):
        xi += 0.01
    x.append(xi)

plt.xlabel('x')
plt.hist(x,50,fc='g',ec='k')
plt.show()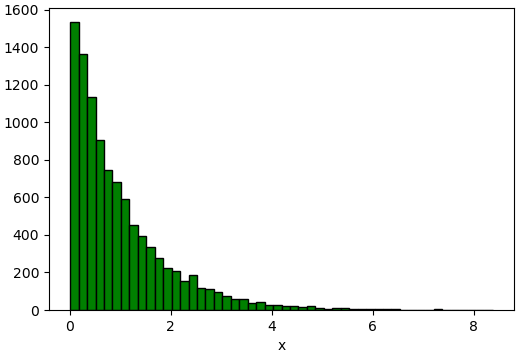

และวาดกราฟ PPF ได้ดังนี้

q = np.linspace(0,1,101)[:-1]
x = []
for u in q:
    xi = 0
    while(u>pdf(xi)):
        xi += 0.01
    x.append(xi)

plt.xlabel('$F_X(x)$')
plt.ylabel('x')
plt.plot(q,x,'g')
plt.show()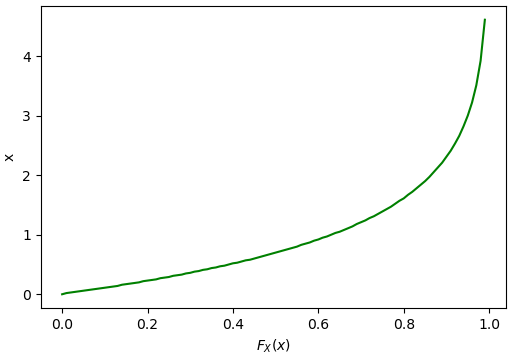

เพียงแต่ว่าจริงๆแล้วในทางปฏิบัตินั้น การแจกแจงแบบต่อเนื่องสามารถคำนวณค่าผกผันของความน่าจะเป็นสะสมได้โดยตรง ดังนั้นวิธีที่ง่ายกว่านั้นก็คือสุ่มค่าแล้วคำนวณ PPF เท่านี้ค่าที่ได้ก็จะมีการแจกแจงเป็นไปตามที่ต้องการแล้ว

สำหรับกรณีของการแจกแจงแบบเลขชี้กำลังในตัวอย่างนี้คือ


ดังนั้น PPF คือ


เมื่อรู้ PPF แบบนี้แล้วก็เขียนฟังก์ชันคำนวณโดยตรง แบบนี้ก็จะได้การแจกแจงในรูปแบบที่ต้องการโดยอย่างง่ายดาย

def ppf(u):
    return -np.log(1-u)

u = np.random.random(10000) # สุ่มค่า
x = ppf(u) # นำค่าที่สุ่มมาคำนวณ PPF
plt.xlabel('x')
plt.hist(x,50,fc='g',ec='k')
plt.show()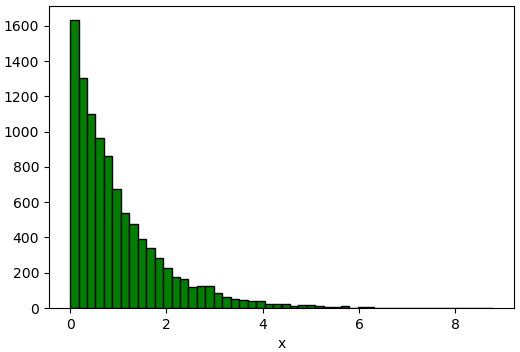

ผลที่ได้ออกมาในลักษณะเดียวกับตัวอย่างก่อนหน้า แต่คำนวณได้ทันทีเร็วกว่ามาก

ในทางปฏิบัติ วิธีนี้ก็เป็นวิธีการที่มีประสิทธิภาพในการจำลองการแจกแจงแบบเลขชี้กำลังจริงๆ เพราะเป็นการแจกแจงที่สามารถหา PPF ได้ง่าย

แต่น่าเสียดายว่าแม้จะรู้ฟังก์ชันการแจกแจง ก็อาจไม่สามารถหา PPF ได้เสมอไป หรือถึงหาได้ก็อาจไม่ได้คำนวณได้ง่ายนัก

ส่วนกรณีของการแจกแจงแบบไม่ต่อเนื่อง นั้นไม่สามารถเขียน PPF ออกมาเป็นสมการเพื่อคำนวณโดยตรงแบบนี้ได้ จึงได้แต่ไล่วนเทียบทีละขั้น จึงอาจไม่เหมาะที่จะใช้วิธีนี้ในทางปฏิบัติจริงๆ

ดังนั้นที่จะใช้วิธีนี้ โดยหลักแล้วก็จะจำกัดอยู่ที่การแจกแจงแบบต่อเนื่องบางแบบที่คำนวณ PPF ได้ง่าย

อนึ่ง ที่จริงหากใช้เมธอด .ppf() ของ scipy.stats แล้วก็จะสามารถคำนวณ PPF ของการแจกแจงทุกประเภทได้

เช่นลองฟังก์ชันเบตา

import scipy.stats
beta = scipy.stats.beta(9,3)
u = np.random.random(10000)
x = beta.ppf(u)
plt.xlabel('x')
plt.hist(x,50,fc='g',ec='k')
plt.show()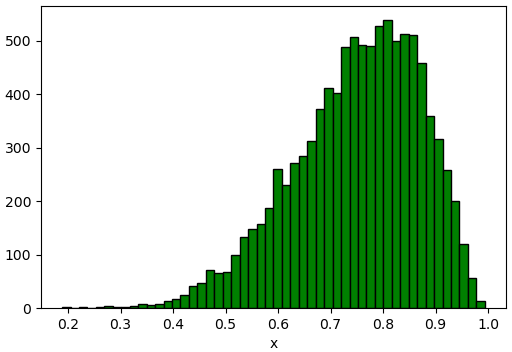

เพียงแต่จริงๆแล้วถ้าจะใช้ scipy.stats อยู่ตั้งแต่แรกแล้วก็สุ่มค่าโดยใช้ .rvs() ไปเลยโดยตรงย่อมจะมีประสิทธิภาพกว่า ไม่ได้จำเป็นต้องแปลงจาก PPF อีกที

x = beta.rvs(10000)

ยกตัวอย่างง่ายๆอีกตัวอย่างหนึ่งเพื่อให้เห็นมากขึ้น คือ เช่น


ซึ่งก็คือฟังก์ชันง่ายๆที่ค่าแปรตาม x ไปจนสุดที่ 2

แบบนี้ความน่าจะเป็นสะสมหาได้เป็น


แล้วก็จะหาฟังก์ชันส่วนกลับ PPF ได้เป็น


เขียนโค้ดได้เป็น

def ppf(u):
    return 2*np.sqrt(u)
u = np.random.random(10000)
x = ppf(u)
plt.xlabel('x')
plt.hist(x,50,fc='#dbf4ff',ec='k')
plt.show()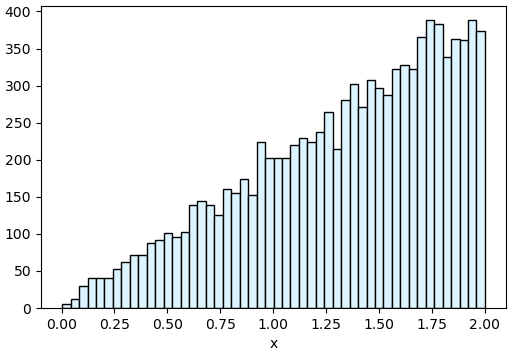

การแปลงกลับ

แถมท้ายอีกนิดเพื่อความเข้าใจที่มากขึ้นอีก นั่นคือจริงๆแล้วด้วยแนวคิดนี้ แสดงว่าถ้าหากเราสุ่มค่าให้มีการแจกแจงแบบไหน แล้วเอาค่าที่ได้มาคูณด้วยฟังก์ชันความน่าจะเป็นสะสม ผลที่ได้ก็จะกลายเป็นการแจกแจงแบบเอกรูป

เช่น

expon = scipy.stats.expon(0,1)
u = expon.rvs(10000) # สุ่มค่าด้วยการแจกแจงแบบแบบเลขชี้กำลัง
x = expon.cdf(u) # แปลงค่าด้วย CDF ผลที่ได้กลับกลายเป็นการแจกแจงเอกรูป
plt.xlabel('x')
plt.hist(x,50,fc='#297174',ec='k')
plt.show()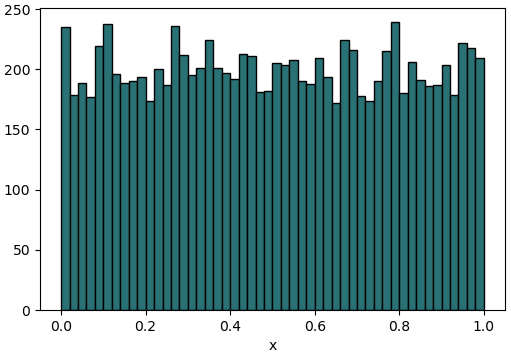

เริ่มสุ่มโดยแจกแจงแบบแบบเลขชี้กำลัง แต่สุดท้ายก็กลับมากลายเป็นการแจกแจงแบบเอกรูปไป

~ 自己紹介 ~

目次

日本による名言集

python モジュール -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 機械学習 -- ニューラル      ネットワーク

javascript

モンゴル語

言語学

maya

確率論

日本での日記

中国での日記 -- 北京での日記 -- 香港での日記 -- 澳門での日記

台灣での日記

北欧での日記

他の国での日記

qiita

その他の記事

記事の類別

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --MATLAB --SQL --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม --สเตเบิลดิฟฟิวชัน ---comfyui -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ -ซางะ -นางาซากิ -คุมาโมโตะ -โออิตะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ -ออสเตรเลีย ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม เรื่องแต่ง บันทึก

　 記事を検索

　 最新記事

　 おすすめの記事

月別記事

もっと前の記事

ไทย

日本語

中文