pytorch เบื้องต้น บทที่ ๙: ดรอปเอาต์และแบตช์นอร์ม
เขียนเมื่อ 2018/09/08 10:16
แก้ไขล่าสุด 2022/07/09 15:54
>> ต่อจาก บทที่ ๘
ดรอปเอาต์ (dropout) และแบตช์นอร์ม (batch norm) เป็นชั้นที่มักถูกเสริมเข้ามาภายในโครงข่ายประสาทเทียมเพื่อเป็นตัวช่วยในการเรียนรู้ของโครงข่าย
รายละเอียดเรื่องดรอปเอาต์อ่านในโครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๗
ส่วนเรื่องแบตช์นอร์มอ่านในโครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๘
ใน pytorch ก็ได้เตรียมชั้นของดรอปเอาต์และแบตช์นอร์มไว้
ดรอปเอาต์
ชั้นของดรอปเอาต์คือ torch.nn.Dropout
p คือค่าที่กำหนดว่าจะดรอปไปเป็นสัดส่วนเท่าไหร่ ถ้า p=0.2 แสดงว่าดรอปไป 0.2 เหลือ 0.8
แบตช์นอร์ม
ชั้นของแบตช์นอร์ม จะแยกใช้ขึ้นกับมิติของข้อมูล ถ้าเป็นข้อมูลทั่วไปใช้ torch.nn.BatchNorm1d แต่สำหรับโครงข่ายประสาทแบบคอนโวลูชันสองมิติ จะใช้ torch.nn.BatchNorm2d สามมิติจะใช้ torch.nn.BatchNorm3d แต่ไม่ว่าจะอันไหนก็มีลักษณะการทำงานโดยรวมเหมือนกัน ต่างกันที่มิติของข้อมูลที่ป้อนเข้ามา
BatchNorm1d มีค่าตัวเลือกที่สามารถใส่ได้ขณะสร้างคือ
- num_features จำนวนตัวแปรของข้อมูล
- eps ค่าเล็กๆที่ใช้บวกกับส่วนเบี่ยเบนมาตรฐานขณะหารเพื่อกันการหาร 0 ค่าตั้งต้นคือ 1e-5
- momentum โมเมนตัม ค่าตั้งต้นคือ 0.1
- affine กำหนดว่าจะมีการคำนวณเชิงเส้น โดยคูณ γ บวก β หรือไม่ ค่าตั้งต้นคือ True
- track_running_stats กำหนดว่าจะให้คำนวณค่าเฉลี่ยและความแปรปรวนขณะวิ่งหรือไม่ ค่าตั้งต้นคือ True
ถ้า affine เป็น False (หรือ 0) ชั้นแบตช์นอร์มนี้ก็จะไม่มีพารามิเตอร์ที่ต้องทำการเรียนรู้
โมเมนตัมในที่นี้ความหมายตรงกันข้ามกับในเนื้อหาโครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๘ กล่าวคือ
..(9.1)
เมื่อ m คือโมเมนตัม μR คือค่าเฉลี่ยขณะวิ่ง μB คือค่าใหม่ σR คือส่วนเบี่ยงเบนมาตรฐานขณะวิ่ง σB คือค่าใหม่
แต่ใน chainer และ keras ต่างก็ใช้ในความหมายเดียวกันนี้ มีแต่ pytorch ที่ใช้ตรงกันข้าม ดังนั้นอาจต้องระวังตรงนี้ด้วย
ค่าตั้งต้นของโมเมนตัมในที่นี้คือ 0.1 ซึ่งตรงกันข้ามกับ chainer ที่เป็น 0.9 และ keras ที่เป็น 0.99 ดังนั้นต่อให้ไม่ได้ใส่ใจตั้งค่าตรงนี้ผลที่ได้ก็ไม่ต่างกันมาก
track_running_stats นั้นถ้ากำหนดให้เป็น False ไป จะไม่มีการคำนวณค่าเฉลี่ยและความแปรปรวนขณะวิ่ง แล้วทำให้ไม่มีความแตกต่างระหว่างฝึกและตรวจสอบ
การแยกกรณีระหว่างการฝึกและการตรวจสอบ
ทั้งดรอปเอาต์และแบตช์นอร์มมีสิ่งที่ต้องระวังเหมือนกันก็คือการที่วิธีการคำนวณในชั้นจะต่างกันไปในระหว่างการเรียนรู้กับการตรวจสอบใช้งาน ดังนั้นจึงต้องนำมาพูดถึงเป็นพิเศษ
ออบเจ็กต์คลาส Module จะมีเมธอดชื่อ .eval() กับ .train() เป็นตัวสำหรับปรับโหมดเพื่อแยกว่ากำลังฝึกอยู่หรือกำลังตรวจสอบ
ในขณะที่ฝึกอยู่ ให้ปรับโหมดเป็นโหมดฝึก โดยใช้ .train() แต่พอจะทดสอบให้ปรับเป็นโหมดตรวจสอบโดยใช้ .eval()
หากไม่ได้ไปทำอะไร ค่าตั้งต้นเริ่มแรกจะอยู่ที่โหมดฝึก
การจะดูว่าอยู่ในโหมดฝึกหรือเปล่าให้ดูที่ .training
ลองใช้ดู
.eval() กับ .train() นั้นไม่ได้มีอยู่แค่ในชั้นดรอปเอาต์กับแบตช์นอร์ม แต่เป็นเมธอดสำหรับออบเจ็กคลาส Module ทั้งหมด เพียงแต่สำหรับตัวอื่นใช้ไปก็ไม่มีผลอะไร
และถ้าหากใช้กับ Module ที่บรรจุ Module อื่นอยู่ ตัวข้างในก็จะได้ผลนั้นไปด้วย
ดังนั้นเวลาใช้ เราแค่สั่ง .train() กับ .eval() ให้กับตัว Module ใหญ่สุดครั้งเดียวก็จะเป็นการเปลี่ยนโหมดของทั้งระบบ
การนำมาใช้จริง
ต่อไปเป็นตัวอย่างของการสร้างโครงข่ายประสาทที่มีการนำแบตช์นอร์มและดรอปเอาต์มาใช้
ยกตัวอย่างโดยสร้างข้อมูลแบบนี้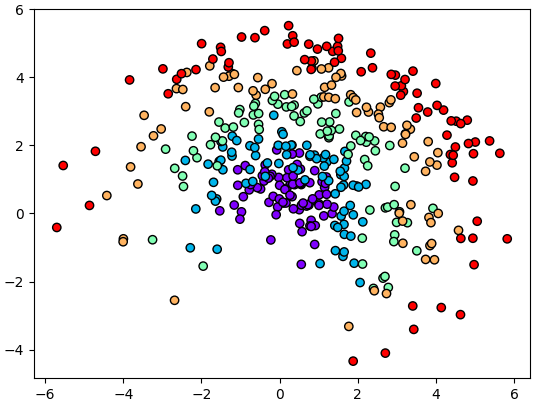
ลองสร้างโครงข่ายแบบนี้
เวลาสร้างจะเลือกได้ว่าจะให้มีดรอปเอาต์กับแบตช์นอร์มหรือไม่ ถ้ามีก็จะสร้างชั้นขึ้นมาแทรกระหว่าง lin กับ ReLU
ในขั้นตอนการฝึกจะเรียกใช้ .train() ก่อนทำการคำนวณไปข้างหน้าและแพร่ย้อนกลับเพื่อฝึก หลังจากนั้นใช้ .eval() เพื่อทำนายแล้วคำนวณคะแนนในแต่ละขั้น
ในที่นี้ทำเมธอดทำนายแยกไว้ ๒ ตัว .thamnai_() เอาไว้ใช้ด้านในตัวคลาสขณะฝึก ส่วน .thamnai() จะเอาไว้ใช้นอกคลาส โดยข้อมูลป้อนเข้าเป็นอาเรย์ก็ได้ ข้างในจะทำการแปลงเป็นเทนเซอร์แล้วเรียกใช้ .thamnai_() อีกที เสร็จแล้วก็แปลงกลับเป็นอาเรย์
ลองสร้างโครงข่ายสัก ๔ ชั้น เทียบกรณีที่มีและไม่มีดรอปเอาต์กับแบตช์นอร์ม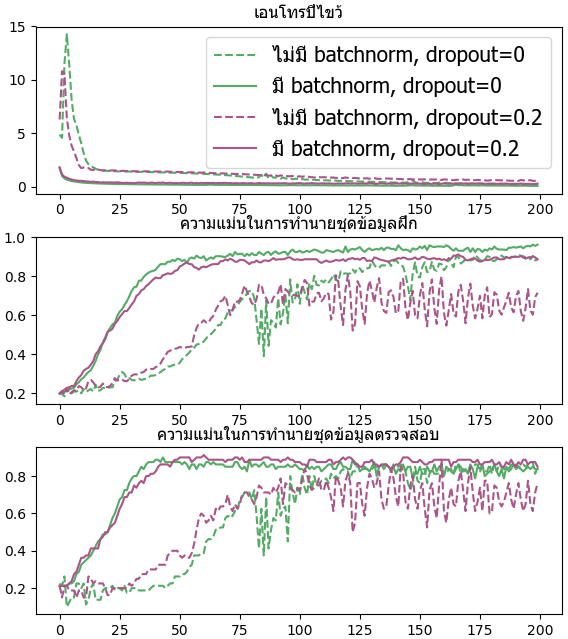
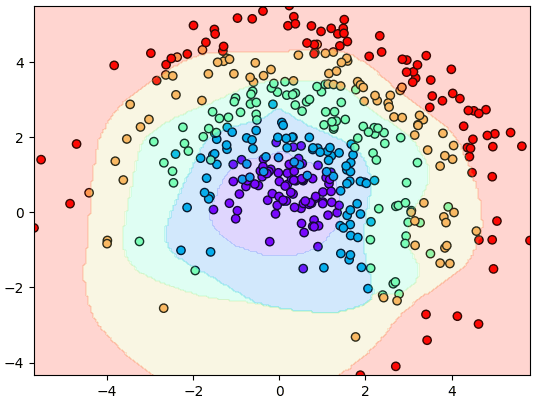
จะเห็นว่าแบตช์นอร์มทำให้การเรียนรู้คืบหน้าไปเร็วกว่ามาก ไม่ว่าจะกรณีที่มีดรอปเอาต์หรือไม่ก็ตาม
>> อ่านต่อ บทที่ ๑๐
ดรอปเอาต์ (dropout) และแบตช์นอร์ม (batch norm) เป็นชั้นที่มักถูกเสริมเข้ามาภายในโครงข่ายประสาทเทียมเพื่อเป็นตัวช่วยในการเรียนรู้ของโครงข่าย
รายละเอียดเรื่องดรอปเอาต์อ่านในโครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๗
ส่วนเรื่องแบตช์นอร์มอ่านในโครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๘
ใน pytorch ก็ได้เตรียมชั้นของดรอปเอาต์และแบตช์นอร์มไว้
ดรอปเอาต์
ชั้นของดรอปเอาต์คือ torch.nn.Dropout
do = torch.nn.Dropout()
print(do) # ได้ Dropout(p=0.5, inplace=False)
do = torch.nn.Dropout(0.2)
print(do) # ได้ Dropout(p=0.2, inplace=False)p คือค่าที่กำหนดว่าจะดรอปไปเป็นสัดส่วนเท่าไหร่ ถ้า p=0.2 แสดงว่าดรอปไป 0.2 เหลือ 0.8
แบตช์นอร์ม
ชั้นของแบตช์นอร์ม จะแยกใช้ขึ้นกับมิติของข้อมูล ถ้าเป็นข้อมูลทั่วไปใช้ torch.nn.BatchNorm1d แต่สำหรับโครงข่ายประสาทแบบคอนโวลูชันสองมิติ จะใช้ torch.nn.BatchNorm2d สามมิติจะใช้ torch.nn.BatchNorm3d แต่ไม่ว่าจะอันไหนก็มีลักษณะการทำงานโดยรวมเหมือนกัน ต่างกันที่มิติของข้อมูลที่ป้อนเข้ามา
BatchNorm1d มีค่าตัวเลือกที่สามารถใส่ได้ขณะสร้างคือ
- num_features จำนวนตัวแปรของข้อมูล
- eps ค่าเล็กๆที่ใช้บวกกับส่วนเบี่ยเบนมาตรฐานขณะหารเพื่อกันการหาร 0 ค่าตั้งต้นคือ 1e-5
- momentum โมเมนตัม ค่าตั้งต้นคือ 0.1
- affine กำหนดว่าจะมีการคำนวณเชิงเส้น โดยคูณ γ บวก β หรือไม่ ค่าตั้งต้นคือ True
- track_running_stats กำหนดว่าจะให้คำนวณค่าเฉลี่ยและความแปรปรวนขณะวิ่งหรือไม่ ค่าตั้งต้นคือ True
ถ้า affine เป็น False (หรือ 0) ชั้นแบตช์นอร์มนี้ก็จะไม่มีพารามิเตอร์ที่ต้องทำการเรียนรู้
bn = torch.nn.BatchNorm1d(5)
print(bn) # ได้ BatchNorm1d(5, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
print(bn.weight) # ได้ Parameter containing: tensor([1., 1., 1., 1., 1.], requires_grad=True)
print(bn.bias) # ได้ Parameter containing: tensor([0., 0., 0., 0., 0.], requires_grad=True)
bn = torch.nn.BatchNorm1d(5,affine=0)
print(bn) # ได้ BatchNorm1d(5, eps=1e-05, momentum=0.1, affine=0, track_running_stats=True)
print(bn.weight) # ได้ None
print(bn.bias) # ได้ Noneโมเมนตัมในที่นี้ความหมายตรงกันข้ามกับในเนื้อหาโครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๘ กล่าวคือ
..(9.1)
เมื่อ m คือโมเมนตัม μR คือค่าเฉลี่ยขณะวิ่ง μB คือค่าใหม่ σR คือส่วนเบี่ยงเบนมาตรฐานขณะวิ่ง σB คือค่าใหม่
แต่ใน chainer และ keras ต่างก็ใช้ในความหมายเดียวกันนี้ มีแต่ pytorch ที่ใช้ตรงกันข้าม ดังนั้นอาจต้องระวังตรงนี้ด้วย
ค่าตั้งต้นของโมเมนตัมในที่นี้คือ 0.1 ซึ่งตรงกันข้ามกับ chainer ที่เป็น 0.9 และ keras ที่เป็น 0.99 ดังนั้นต่อให้ไม่ได้ใส่ใจตั้งค่าตรงนี้ผลที่ได้ก็ไม่ต่างกันมาก
track_running_stats นั้นถ้ากำหนดให้เป็น False ไป จะไม่มีการคำนวณค่าเฉลี่ยและความแปรปรวนขณะวิ่ง แล้วทำให้ไม่มีความแตกต่างระหว่างฝึกและตรวจสอบ
การแยกกรณีระหว่างการฝึกและการตรวจสอบ
ทั้งดรอปเอาต์และแบตช์นอร์มมีสิ่งที่ต้องระวังเหมือนกันก็คือการที่วิธีการคำนวณในชั้นจะต่างกันไปในระหว่างการเรียนรู้กับการตรวจสอบใช้งาน ดังนั้นจึงต้องนำมาพูดถึงเป็นพิเศษ
ออบเจ็กต์คลาส Module จะมีเมธอดชื่อ .eval() กับ .train() เป็นตัวสำหรับปรับโหมดเพื่อแยกว่ากำลังฝึกอยู่หรือกำลังตรวจสอบ
ในขณะที่ฝึกอยู่ ให้ปรับโหมดเป็นโหมดฝึก โดยใช้ .train() แต่พอจะทดสอบให้ปรับเป็นโหมดตรวจสอบโดยใช้ .eval()
หากไม่ได้ไปทำอะไร ค่าตั้งต้นเริ่มแรกจะอยู่ที่โหมดฝึก
การจะดูว่าอยู่ในโหมดฝึกหรือเปล่าให้ดูที่ .training
ลองใช้ดู
do = torch.nn.Dropout()
print(do.training) # ได้ True
do.eval()
print(do.training) # ได้ False
do.train()
print(do.training) # ได้ True.eval() กับ .train() นั้นไม่ได้มีอยู่แค่ในชั้นดรอปเอาต์กับแบตช์นอร์ม แต่เป็นเมธอดสำหรับออบเจ็กคลาส Module ทั้งหมด เพียงแต่สำหรับตัวอื่นใช้ไปก็ไม่มีผลอะไร
และถ้าหากใช้กับ Module ที่บรรจุ Module อื่นอยู่ ตัวข้างในก็จะได้ผลนั้นไปด้วย
seq = torch.nn.Sequential(torch.nn.Dropout(),torch.nn.BatchNorm1d(10))
print(seq[0].training,seq[1].training) # ได้ True True
seq.eval()
print(seq[0].training,seq[1].training) # ได้ False Falseดังนั้นเวลาใช้ เราแค่สั่ง .train() กับ .eval() ให้กับตัว Module ใหญ่สุดครั้งเดียวก็จะเป็นการเปลี่ยนโหมดของทั้งระบบ
การนำมาใช้จริง
ต่อไปเป็นตัวอย่างของการสร้างโครงข่ายประสาทที่มีการนำแบตช์นอร์มและดรอปเอาต์มาใช้
ยกตัวอย่างโดยสร้างข้อมูลแบบนี้
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(8)
z = np.arange(5).repeat(80)
r = np.random.normal(z+1,0.35)
t = np.random.normal(1,1,400)
x = r*np.cos(t)
y = r*np.sin(t)
X = np.array([x,y]).T
plt.scatter(x,y,c=z,edgecolor='k',cmap='rainbow')
plt.show()
ลองสร้างโครงข่ายแบบนี้
import torch
relu = torch.nn.ReLU()
ha_entropy = torch.nn.CrossEntropyLoss()
class Prasat(torch.nn.Sequential):
def __init__(self,m,eta=0.01,dropout=0,bn=0):
super(Prasat,self).__init__()
nm = len(m)
for i in range(1,nm):
lin = torch.nn.Linear(m[i-1],m[i])
torch.nn.init.kaiming_normal_(lin.weight)
lin.bias.data.fill_(0)
self.add_module('lin%d'%i,lin)
if(i<nm-1):
if(bn): # สร้างชั้นแบตช์นอร์ม
self.add_module('bano%d'%i,torch.nn.BatchNorm1d(m[i]))
if(dropout): # สร้างชั้นดรอปเอาต์
self.add_module('droa%d'%i,torch.nn.Dropout(dropout))
self.add_module('relu%d'%i,relu)
self.opt = torch.optim.Adam(self.parameters(),lr=eta)
def rianru(self,X,z,X_truat,z_truat,n_thamsam):
X = torch.Tensor(X)
z = torch.LongTensor(z)
X_truat = torch.Tensor(X_truat)
z_truat = torch.LongTensor(z_truat)
self.entropy = []
self.khanaen_fuek = []
self.khanaen_truat = []
for o in range(n_thamsam):
self.train() # ปรับเป็นโหมดฝึก
a = self(X)
J = ha_entropy(a,z)
J.backward()
self.opt.step()
self.opt.zero_grad()
self.entropy.append(float(J)) # เอนโทรปี
self.eval() # ปรับเป็นโหมดทดสอบ
self.khanaen_fuek.append(self.ha_khanaen_(X,z)) # คะแนนทำนายชุดข้อมูลฝึก
self.khanaen_truat.append(self.ha_khanaen_(X_truat,z_truat)) # คำแนนทำนายชุดข้อมูลตรวจสอบ
def thamnai(self,X):
X = torch.Tensor(X)
return self.thamnai_(X).numpy()
def thamnai_(self,X):
return self(X).argmax(1)
def ha_khanaen_(self,X,z):
return (self.thamnai_(X)==z).numpy().mean()เวลาสร้างจะเลือกได้ว่าจะให้มีดรอปเอาต์กับแบตช์นอร์มหรือไม่ ถ้ามีก็จะสร้างชั้นขึ้นมาแทรกระหว่าง lin กับ ReLU
ในขั้นตอนการฝึกจะเรียกใช้ .train() ก่อนทำการคำนวณไปข้างหน้าและแพร่ย้อนกลับเพื่อฝึก หลังจากนั้นใช้ .eval() เพื่อทำนายแล้วคำนวณคะแนนในแต่ละขั้น
ในที่นี้ทำเมธอดทำนายแยกไว้ ๒ ตัว .thamnai_() เอาไว้ใช้ด้านในตัวคลาสขณะฝึก ส่วน .thamnai() จะเอาไว้ใช้นอกคลาส โดยข้อมูลป้อนเข้าเป็นอาเรย์ก็ได้ ข้างในจะทำการแปลงเป็นเทนเซอร์แล้วเรียกใช้ .thamnai_() อีกที เสร็จแล้วก็แปลงกลับเป็นอาเรย์
ลองสร้างโครงข่ายสัก ๔ ชั้น เทียบกรณีที่มีและไม่มีดรอปเอาต์กับแบตช์นอร์ม
sumlueak = np.random.permutation(len(z))
X_fuek,X_truat = X[sumlueak[:320]],X[sumlueak[320:]]
z_fuek,z_truat = z[sumlueak[:320]],z[sumlueak[320:]]
plt.figure(figsize=(6,9))
ax1 = plt.subplot(311)
ax1.set_title(u'เอนโทรปีไขว้',family='Tahoma',size=12)
ax2 = plt.subplot(312)
ax2.set_title(u'ความแม่นในการทำนายชุดข้อมูลฝึก',family='Tahoma',size=12)
ax3 = plt.subplot(313)
ax3.set_title(u'ความแม่นในการทำนายชุดข้อมูลตรวจสอบ',family='Tahoma',size=12)
for dropout in [0,1]:
for bn in [0,1]:
prasat = Prasat([2,300,300,300,5],eta=0.005,dropout=dropout*0.2,bn=bn)
prasat.rianru(X_fuek,z_fuek,X_truat,z_truat,200)
ls = ['--','-'][bn]
si = ['#55aa66','#aa5588'][dropout]
ax1.plot(prasat.entropy,si,ls=ls)
ax2.plot(prasat.khanaen_fuek,si,ls=ls)
ax3.plot(prasat.khanaen_truat,si,ls=ls)
ax1.legend([u'ไม่มี batchnorm, dropout=0',
u'มี batchnorm, dropout=0',
u'ไม่มี batchnorm, dropout=0.2',
u'มี batchnorm, dropout=0.2'],
prop={'family':'Tahoma','size':15})
plt.tight_layout()
plt.show()
plt.figure()
mx,my = np.meshgrid(np.linspace(x.min(),x.max(),200),np.linspace(y.min(),y.max(),200))
mX = torch.Tensor(np.array([mx.ravel(),my.ravel()]).T)
mz = prasat.thamnai(mX).reshape(200,200)
plt.xlim(x.min(),x.max())
plt.ylim(y.min(),y.max())
plt.scatter(x,y,c=z,edgecolor='k',cmap='rainbow')
plt.contourf(mx,my,mz,alpha=0.2,cmap='rainbow')
plt.show()

จะเห็นว่าแบตช์นอร์มทำให้การเรียนรู้คืบหน้าไปเร็วกว่ามาก ไม่ว่าจะกรณีที่มีดรอปเอาต์หรือไม่ก็ตาม
>> อ่านต่อ บทที่ ๑๐
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> pytorch