โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๘: การเร่งการเรียนรู้ด้วยแบตช์นอร์ม
เขียนเมื่อ 2018/09/02 06:36
แก้ไขล่าสุด 2022/07/10 21:08
>> ต่อจาก บทที่ ๑๗
แนวคิด
ในบทที่ ๑๓ ได้พูดถึงไปแล้วว่าถ้าหากค่าของตัวแปรระหว่างไหลผ่านในแต่ละชั้นอยู่ในช่วงที่พอเหมาะก็จะทำให้การเรียนรู้เป็นไปได้อย่างราบรื่นดีกว่า เพื่อการนั้นจึงต้องใส่ใจกับค่าพารามิเตอร์ตั้งต้น
แต่ตอนหลังก็ได้มีคนคิดค้นอีกวิธีหนึ่ง คือให้หาทางควบคุมให้ค่าในแต่ละชั้นอยู่ภายในช่วงที่เหมาะสมตลอดเวลา
วิธีนั้นทำได้โดยการเพิ่มชั้นที่เรียกว่าแบตช์นอร์ม (batch norm) แทรกลงไปก่อนหน้าหรือหลังฟังก์ชันกระตุ้นในแต่ละชั้น
ถ้าแทรกก่อน โครงสร้างการจัดเรียงชั้นอาจเขียนได้เป็นในลักษณะแบบนี้ สำหรับโครงข่าย ๔ ชั้น

นี่เป็นเทคนิคที่ถูกคิดขึ้นมาในปี 2015 แต่ได้รับความนิยมสูงมากอย่างรวดเร็ว
แบตช์นอร์มมีความสามารถดังนี้
- ทำให้การเรียนรู้คืบหน้าไปได้อย่างรวดเร็วขึ้น
- ทำให้ไม่ต้องใส่ใจกับค่าพารามิเตอร์ตั้งต้นมากนัก
- ป้องกันการเรียนรู้เกินได้
ทั้งหมดนี้เป็นผลจากการที่ค่าในระหว่างแต่ละชั้นถูกปรับให้อยู่ในช่วงที่เหมาะสม
วิธีการ
ชั้นแบตช์นอร์มจะทำการปรับค่าข้อมูลที่ผ่านให้เป็นมาตรฐานโดยเทียบกับข้อมูลทั้งหมด
..(18.1)
โดยในที่นี้ x คือค่าตัวแปรต่างๆในแต่ละชั้น เสร็จแล้วก็จะได้ค่า xC ที่มีค่าเฉลี่ยเป็น 0 ส่วนเบี่ยงเบนมาตรฐานเป็น 1
แต่การคำนวณในชั้นนี้ยังไม่จบแค่นั้น ยังต้องมีการไปคูณและบวกกับพารามิเตอร์เพื่อปรับค่าให้เหมาะสมอีกที
..(18.2)
โดย γ และ β เป็นพารามิเตอร์ที่ต้องทำการเรียนรู้
เพียงแต่ γ และ β ในบางการใช้งานอาจตัดตรงส่วนนี้ทิ้งไป คือตั้งให้ γ=1 และ β=0 คงที่ แบบนี้ก็จะไม่มีพารามิเตอร์ให้ต้องเรียนรู้ ทำให้ประหยัดการคำนวณและหน่วยความจำที่ต้องใช้ภายในชั้นนี้ไปได้เล็กน้อย (ถ้าเป็นใน pytorch ตอนสร้างกำหนดให้ affine=0 ก็จะตัดส่วนนี้ทิ้งไป)
ยังมีอีกปัญหาหนึ่งก็คือ ค่าที่ผ่านชั้นแบตช์นอร์มไปนั้นคือค่าที่ปรับให้เป็นมาตรฐานเทียบกับค่าที่ถูกป้อนมาด้วยกันในครั้งนั้น แบบนี้แสดงว่าแต่ละครั้งที่ป้อนค่าเข้ามาต่อให้ป้อนค่าเดิมแต่ถ้าค่าอื่นไม่เหมือนเดิมคำตอบที่ได้จะไม่เหมือนเดิม
แบบนี้แม้เวลาที่ฝึกจะทำให้การเรียนรู้คืบหน้าไปได้เร็วจริง แต่พอจะใช้งานจริงคำตอบจะไม่แน่นอน ขึ้นอยู่กับชุดข้อมูลที่ป้อนเข้ามาด้วยกัน
ดังนั้น จึงต้องทำการแยกกรณีเวลาที่ฝึกกับเวลาที่ใช้งานจริงออกจากกัน ซึ่งจะคล้ายกับการใช้ดรอปเอาต์ ดังที่แนะนำไปแล้วในบทที่ ๑๗
เวลาใช้งานจริงค่าจะต้องไม่เปลี่ยนไป ไม่ว่าจะป้อนข้อมูลผ่านเข้ามาทีละตัว หรือทีละหลายตัว
xN จะคำนวณโดย
..(18.3)
โดย μR คือ ค่าเฉลี่ยขณะวิ่ง σR คือส่วนเบี่ยงเบนมาตรฐานขณะวิ่ง เป็นค่าที่ปรับเปลี่ยนไปในระหว่างการเรียนรู้ คำนวณโดย
..(18.4)
จากนั้นก็คำนวณ xB โดยเข้าสมการ (18.2) เหมือนเดิม
โดย m คือค่าโมเมนตัม เป็นค่าที่สามารถปรับได้ โดยทั่วไปจะให้มีค่าใกล้ๆ 1 อย่างเช่น m=0.9 เพื่อให้มีความเปลี่ยนแปลงไปเล็กน้อยจากข้อมูลในแต่ละรอบ
**หมายเหตุ: โมเมนตัมในที่นี้นิยามในความหมายเดียวกับ keras แต่ใน pytorch จะใช้ในความหมายตรงกันข้าม
ระหว่างการเรียนรู้ ค่า μR กับ σR ก็จะเปลี่ยนแปลงไปตลอด เช่นเดียวกับพารามิเตอร์ γ และ β แต่พอเรียนรู้เสร็จก็จะกลายเป็นค่าคงที่ ซึ่งต่างจาก μB และ σB ซึ่งจะเปลี่ยนไปตลอดโดยขึ้นกับชุดข้อมูลป้อนเข้า
หลักการและวิธีการมีอยู่เท่านี้ สำหรับเรื่องการหาอนุพันธ์ขณะแพร่ย้อนกลับนั้นก็แค่คำนวณย้อนตามกฎลูกโซ่ ในที่นี้ขอละไว้ ดูจากในโค้ดเอาได้
เขียนคลาสของแบตช์นอร์ม
ก่อนอื่นนำเข้าชั้นที่จำเป็นต้องใช้ทั้งหมดจาก unagi.py
เราอาจนิยามชั้นแบตช์นอร์มได้แบบนี้
แอตทริบิวต์ .fuekyu คือค่าที่บอกว่ากำลังฝึกอยู่หรือเปล่า เพื่อแยกกรณีฝึกกับกรณีใช้จริง เช่นเดียวกันกับที่ใช้ในดรอปเอาต์
เปรียบเทียบผลของการมีแบตช์นอร์มกับไม่มี
ต่อไปจะยกตัวอย่างการนำชั้นแบตช์นอร์มมาใช้ โดยเราจะเทียบใน ๒ กรณี คือกรณีที่กำหนดค่าพารามิเตอร์น้ำหนักตั้งต้นอย่างเหมาะสมดีแล้ว คือใช้ค่า σ ตั้งต้นแบบเหอ ไข่หมิง (ดูบทที่ ๑๓) และอีกแบบคือใช้ค่าตั้งต้นที่ต่ำเกินควร คือให้ σ เป็น 0.1 เท่าของเหอ ไข่หมิง ทั้ง ๒ กรณีลองทั้งแบบมีแบตช์นอร์มและไม่มี ดังนั้นรวมแล้วเป็น ๔ กรณี
ขอยกตัวอย่างเป็นข้อมูลสองมิติที่กระจายตัวแบบนี้
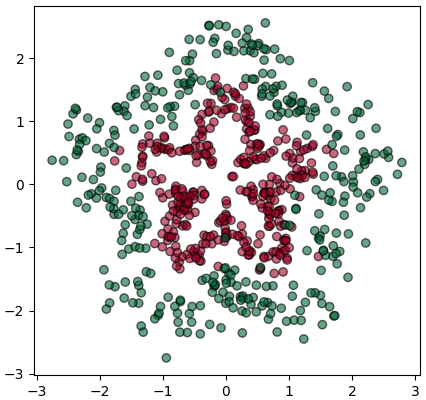
เขียนโครงข่ายประสาท ๔ ชั้นให้ทำการเรียนรู้เพื่อจำแนกกลุ่มข้อมูลแล้วบันทึกความแม่นยำในแต่ละชั้นทั้ง ๔ กรณี แล้ววาดกราฟเปรียบเทียบดูความคืบหน้าในการเรียนรู้
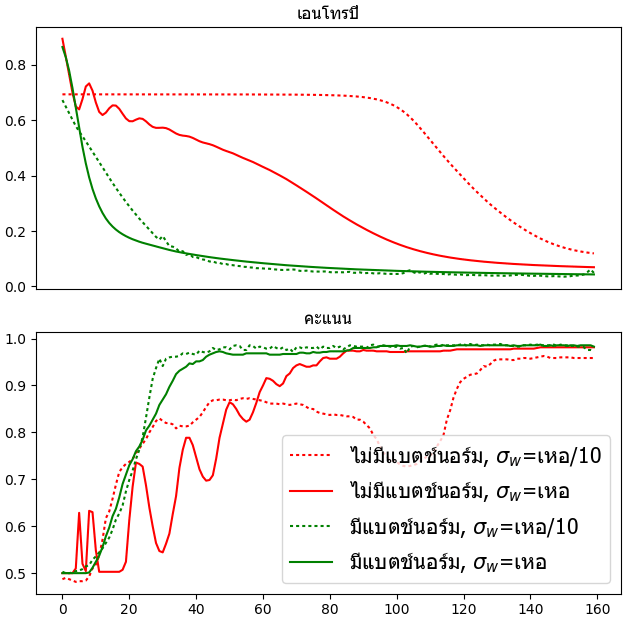
ผลที่ได้จะเห็นได้ว่ากรณีที่ใช้แบตช์นอร์มการเรียนรู้จะไปเร็วกว่าแบบที่ไม่ใช้พอสมควร แถมยังไม่ค่อยเห็นความแตกต่างระหว่างการใช้ค่าเริ่มต้นแบบเหอไข่หมิงกับแบบที่ตั้งให้ต่ำลงสิบเท่าด้วย นั่นแสดงว่าการกำหนดค่าตั้งต้นจะมีความสำคัญน้อยลงมากหากใช้แบตช์นอร์ม
ในขณะที่กรณีที่ไม่ใช่แบตช์นอร์มการเรียนรู้จะไปช้ากว่า แถมจะยิ่งแย่ถ้าหากกำหนดค่าตั้งต้นไม่ดีจะยิ่งเรียนรู้ได้แย่ เห็นผลชัดเจนกว่ามาก
จากตัวอย่างนี้จะเห็นได้ชัดถึงประโยชน์ของแบตช์นอร์ม
>> อ่านต่อ บทที่ ๑๙
แนวคิด
ในบทที่ ๑๓ ได้พูดถึงไปแล้วว่าถ้าหากค่าของตัวแปรระหว่างไหลผ่านในแต่ละชั้นอยู่ในช่วงที่พอเหมาะก็จะทำให้การเรียนรู้เป็นไปได้อย่างราบรื่นดีกว่า เพื่อการนั้นจึงต้องใส่ใจกับค่าพารามิเตอร์ตั้งต้น
แต่ตอนหลังก็ได้มีคนคิดค้นอีกวิธีหนึ่ง คือให้หาทางควบคุมให้ค่าในแต่ละชั้นอยู่ภายในช่วงที่เหมาะสมตลอดเวลา
วิธีนั้นทำได้โดยการเพิ่มชั้นที่เรียกว่าแบตช์นอร์ม (batch norm) แทรกลงไปก่อนหน้าหรือหลังฟังก์ชันกระตุ้นในแต่ละชั้น
ถ้าแทรกก่อน โครงสร้างการจัดเรียงชั้นอาจเขียนได้เป็นในลักษณะแบบนี้ สำหรับโครงข่าย ๔ ชั้น

นี่เป็นเทคนิคที่ถูกคิดขึ้นมาในปี 2015 แต่ได้รับความนิยมสูงมากอย่างรวดเร็ว
แบตช์นอร์มมีความสามารถดังนี้
- ทำให้การเรียนรู้คืบหน้าไปได้อย่างรวดเร็วขึ้น
- ทำให้ไม่ต้องใส่ใจกับค่าพารามิเตอร์ตั้งต้นมากนัก
- ป้องกันการเรียนรู้เกินได้
ทั้งหมดนี้เป็นผลจากการที่ค่าในระหว่างแต่ละชั้นถูกปรับให้อยู่ในช่วงที่เหมาะสม
วิธีการ
ชั้นแบตช์นอร์มจะทำการปรับค่าข้อมูลที่ผ่านให้เป็นมาตรฐานโดยเทียบกับข้อมูลทั้งหมด
..(18.1)
โดยในที่นี้ x คือค่าตัวแปรต่างๆในแต่ละชั้น เสร็จแล้วก็จะได้ค่า xC ที่มีค่าเฉลี่ยเป็น 0 ส่วนเบี่ยงเบนมาตรฐานเป็น 1
แต่การคำนวณในชั้นนี้ยังไม่จบแค่นั้น ยังต้องมีการไปคูณและบวกกับพารามิเตอร์เพื่อปรับค่าให้เหมาะสมอีกที
..(18.2)
โดย γ และ β เป็นพารามิเตอร์ที่ต้องทำการเรียนรู้
เพียงแต่ γ และ β ในบางการใช้งานอาจตัดตรงส่วนนี้ทิ้งไป คือตั้งให้ γ=1 และ β=0 คงที่ แบบนี้ก็จะไม่มีพารามิเตอร์ให้ต้องเรียนรู้ ทำให้ประหยัดการคำนวณและหน่วยความจำที่ต้องใช้ภายในชั้นนี้ไปได้เล็กน้อย (ถ้าเป็นใน pytorch ตอนสร้างกำหนดให้ affine=0 ก็จะตัดส่วนนี้ทิ้งไป)
ยังมีอีกปัญหาหนึ่งก็คือ ค่าที่ผ่านชั้นแบตช์นอร์มไปนั้นคือค่าที่ปรับให้เป็นมาตรฐานเทียบกับค่าที่ถูกป้อนมาด้วยกันในครั้งนั้น แบบนี้แสดงว่าแต่ละครั้งที่ป้อนค่าเข้ามาต่อให้ป้อนค่าเดิมแต่ถ้าค่าอื่นไม่เหมือนเดิมคำตอบที่ได้จะไม่เหมือนเดิม
แบบนี้แม้เวลาที่ฝึกจะทำให้การเรียนรู้คืบหน้าไปได้เร็วจริง แต่พอจะใช้งานจริงคำตอบจะไม่แน่นอน ขึ้นอยู่กับชุดข้อมูลที่ป้อนเข้ามาด้วยกัน
ดังนั้น จึงต้องทำการแยกกรณีเวลาที่ฝึกกับเวลาที่ใช้งานจริงออกจากกัน ซึ่งจะคล้ายกับการใช้ดรอปเอาต์ ดังที่แนะนำไปแล้วในบทที่ ๑๗
เวลาใช้งานจริงค่าจะต้องไม่เปลี่ยนไป ไม่ว่าจะป้อนข้อมูลผ่านเข้ามาทีละตัว หรือทีละหลายตัว
xN จะคำนวณโดย
..(18.3)
โดย μR คือ ค่าเฉลี่ยขณะวิ่ง σR คือส่วนเบี่ยงเบนมาตรฐานขณะวิ่ง เป็นค่าที่ปรับเปลี่ยนไปในระหว่างการเรียนรู้ คำนวณโดย
..(18.4)
จากนั้นก็คำนวณ xB โดยเข้าสมการ (18.2) เหมือนเดิม
โดย m คือค่าโมเมนตัม เป็นค่าที่สามารถปรับได้ โดยทั่วไปจะให้มีค่าใกล้ๆ 1 อย่างเช่น m=0.9 เพื่อให้มีความเปลี่ยนแปลงไปเล็กน้อยจากข้อมูลในแต่ละรอบ
**หมายเหตุ: โมเมนตัมในที่นี้นิยามในความหมายเดียวกับ keras แต่ใน pytorch จะใช้ในความหมายตรงกันข้าม
ระหว่างการเรียนรู้ ค่า μR กับ σR ก็จะเปลี่ยนแปลงไปตลอด เช่นเดียวกับพารามิเตอร์ γ และ β แต่พอเรียนรู้เสร็จก็จะกลายเป็นค่าคงที่ ซึ่งต่างจาก μB และ σB ซึ่งจะเปลี่ยนไปตลอดโดยขึ้นกับชุดข้อมูลป้อนเข้า
หลักการและวิธีการมีอยู่เท่านี้ สำหรับเรื่องการหาอนุพันธ์ขณะแพร่ย้อนกลับนั้นก็แค่คำนวณย้อนตามกฎลูกโซ่ ในที่นี้ขอละไว้ ดูจากในโค้ดเอาได้
เขียนคลาสของแบตช์นอร์ม
ก่อนอื่นนำเข้าชั้นที่จำเป็นต้องใช้ทั้งหมดจาก unagi.py
from unagi import Chan,Affin,Relu,Sigmoid_entropy,Adam,Batchnorm
import numpy as npเราอาจนิยามชั้นแบตช์นอร์มได้แบบนี้
class Batchnorm(Chan):
def __init__(self,m,mmt=0.9):
self.m = m # จำนวนตัวแปรของข้อมูล
self.param = [Param(np.ones(m)),Param(np.zeros(m))] # ค่า γ และ β
self.rmu = np.zeros(m) # ค่าเฉลี่ยขณะวิ่ง
self.rvar = np.zeros(m)+1e-8 # ความแปรปรวนขณะวิ่ง
self.mmt = mmt # โมเมนตัม
self.fuekyu = 1
def pai(self,x):
if(self.fuekyu): # กรณีฝึกอยู่ คำนวณ xn ค่าเฉลี่ยและความแปรปรวนในกลุ่ม
self.n = len(x)
mu = x.mean(0)
self.xc = x-mu
var = (self.xc**2).mean(0)+1e-8
self.sigma = np.sqrt(var)
self.xn = xn = self.xc/self.sigma
self.rmu = self.mmt*self.rmu + (1.-self.mmt)*mu
self.rvar = self.mmt*self.rvar + (1.-self.mmt)*var
else: # กรณีไม่ได้ฝึกอยู่ คำนวณ xn จาก rmu (μR) และ rvar (σR2)
xc = x - self.rmu
xn = xc/np.sqrt(self.rvar)
return self.param[0].kha*xn+self.param[1].kha
def yon(self,g):
self.param[0].g = (g*self.xn).sum(0)
self.param[1].g = g.sum(0)
gxn = self.param[0].kha*g
gsigma = -((gxn*self.xc)/self.sigma**2).sum(0)
gvar = gsigma/self.sigma/2
gxc = gxn/self.sigma + (2./self.n)*self.xc*gvar
gmu = gxc.sum(0)
gx = gxc - gmu/self.n
return gxแอตทริบิวต์ .fuekyu คือค่าที่บอกว่ากำลังฝึกอยู่หรือเปล่า เพื่อแยกกรณีฝึกกับกรณีใช้จริง เช่นเดียวกันกับที่ใช้ในดรอปเอาต์
เปรียบเทียบผลของการมีแบตช์นอร์มกับไม่มี
ต่อไปจะยกตัวอย่างการนำชั้นแบตช์นอร์มมาใช้ โดยเราจะเทียบใน ๒ กรณี คือกรณีที่กำหนดค่าพารามิเตอร์น้ำหนักตั้งต้นอย่างเหมาะสมดีแล้ว คือใช้ค่า σ ตั้งต้นแบบเหอ ไข่หมิง (ดูบทที่ ๑๓) และอีกแบบคือใช้ค่าตั้งต้นที่ต่ำเกินควร คือให้ σ เป็น 0.1 เท่าของเหอ ไข่หมิง ทั้ง ๒ กรณีลองทั้งแบบมีแบตช์นอร์มและไม่มี ดังนั้นรวมแล้วเป็น ๔ กรณี
ขอยกตัวอย่างเป็นข้อมูลสองมิติที่กระจายตัวแบบนี้
import matplotlib.pyplot as plt
n = 350
t = np.random.uniform(0,360,n*2)
r = [np.random.normal(1+0.4*np.sin(np.radians(t[:n])*5),0.2)]
r += [np.random.normal(2+0.4*np.sin(np.radians(t[n:])*5),0.3)]
r = np.hstack(r)
x = r*np.cos(np.radians(t))
y = r*np.sin(np.radians(t))
z = np.repeat([0,1],n)
X = np.array([x,y]).T
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',alpha=0.6,cmap='RdYlGn')
plt.show()
เขียนโครงข่ายประสาท ๔ ชั้นให้ทำการเรียนรู้เพื่อจำแนกกลุ่มข้อมูลแล้วบันทึกความแม่นยำในแต่ละชั้นทั้ง ๔ กรณี แล้ววาดกราฟเปรียบเทียบดูความคืบหน้าในการเรียนรู้
plt.figure(figsize=[6.5,6.5])
ax1 = plt.subplot(211,xticks=[])
ax1.set_title(u'เอนโทรปี',family='Tahoma')
ax2 = plt.subplot(212)
ax2.set_title(u'คะแนน',family='Tahoma')
m = [2,60,60,60,1] # จำนวนเซลล์ในชั้นต่างๆ
n_thamsam = 160 # จำนวนรอบที่ทำซ้ำเพื่อปรับพารามิเตอร์
for b in [0,1]:
for s in [0.1,1]:
# กำหนดแบบจำลอง
chan = []
param = []
for i in range(len(m)-1):
he_kaiming = np.sqrt(2./m[i]) # ค่าน้ำหนักตั้งต้นแบบเหอ ไข่หมิง
af = Affin(m[i],m[i+1],he_kaiming*s)
chan.append(af)
param.extend(af.param)
if(i<len(m)-2):
if(b): # ใส่ชั้นแบตช์นอร์ม
bn = Batchnorm(m[i+1])
chan.append(bn)
param.extend(bn.param)
chan.append(Relu())
chan.append(Sigmoid_entropy())
opt = Adam(param,eta=0.001) # ออปทิไมเซอร์
# เริ่มฝึก
lis_entropy = []
lis_khanaen = []
for i in range(n_thamsam):
# คำนวนไปข้างหน้าในโหมดฝึก เพื่อหาเอนโทรปีแล้วแพร่ย้อนกลับ
X_ = X
for c in chan[:-1]:
c.fuekyu = 1 # ฝึกอยู่
X_ = c(X_)
entropy = chan[-1](X_,z)
lis_entropy.append(entropy.kha) # บันทึกค่าเอนโทรปี
entropy.phraeyon() # แพร่ย้อนกลับ
opt() # ปรับพารามิเตอร์
# คำนวณไปข้างหน้าใหม่ในโหมดใช้งานจริง เพื่อหาคะแนนความแม่นในการทำนาย
X_ = X
for c in chan[:-1]:
c.fuekyu = 0 # ไม่ได้ฝึกอยู่
X_ = c(X_)
lis_khanaen.append(((X_.kha.ravel()>0)==z).mean()) # บันทึกคะแนน
ax1.plot(lis_entropy,[':','-'][s==1],color=['r','g'][b])
ax2.plot(lis_khanaen,[':','-'][s==1],color=['r','g'][b])
plt.legend([u'ไม่มีแบตช์นอร์ม, $\sigma_w$=เหอ/10',
u'ไม่มีแบตช์นอร์ม, $\sigma_w$=เหอ',
u'มีแบตช์นอร์ม, $\sigma_w$=เหอ/10',
u'มีแบตช์นอร์ม, $\sigma_w$=เหอ'],
prop={'family':'Tahoma','size':15})
plt.tight_layout()
plt.show()
ผลที่ได้จะเห็นได้ว่ากรณีที่ใช้แบตช์นอร์มการเรียนรู้จะไปเร็วกว่าแบบที่ไม่ใช้พอสมควร แถมยังไม่ค่อยเห็นความแตกต่างระหว่างการใช้ค่าเริ่มต้นแบบเหอไข่หมิงกับแบบที่ตั้งให้ต่ำลงสิบเท่าด้วย นั่นแสดงว่าการกำหนดค่าตั้งต้นจะมีความสำคัญน้อยลงมากหากใช้แบตช์นอร์ม
ในขณะที่กรณีที่ไม่ใช่แบตช์นอร์มการเรียนรู้จะไปช้ากว่า แถมจะยิ่งแย่ถ้าหากกำหนดค่าตั้งต้นไม่ดีจะยิ่งเรียนรู้ได้แย่ เห็นผลชัดเจนกว่ามาก
จากตัวอย่างนี้จะเห็นได้ชัดถึงประโยชน์ของแบตช์นอร์ม
>> อ่านต่อ บทที่ ๑๙
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy