โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๕: กราฟคำนวณและการแพร่ย้อนกลับ
เขียนเมื่อ 2018/08/26 23:24
แก้ไขล่าสุด 2021/09/28 16:42
>> ต่อจาก บทที่ ๔
กราฟคำนวณ
จะเห็นได้ว่ากว่าจะได้สูตรคำนวณความชันของฟังก์ชันค่าเสียหายเพื่อนำมาใช้คำนวณความเปลี่ยนแปลงของพารามิเตอร์ได้นั้นต้องผ่านการคำนวณด้วยกฎลูกโซ่ต่อเนื่องถึงสามครั้ง
ตรงนี้อาจยังดูเหมือนไม่มีปัญหาอะไรมาก แต่หากลงลึกไปในเนื้อหาการสร้างโครงข่ายประสาทเทียมเรื่อยๆสูตรคำนวณก็จะยิ่งซับซ้อนมากขึ้น
ดังนั้นก่อนที่จะไปต่อ ตรงนี้ขอแนะนำวิธีการเขียนแผนผังแสดงความสัมพันธ์ของตัวแปร ซึ่งจะช่วยให้เห็นภาพและเข้าใจการคำนวณภายในโครงข่ายประสาทเทียมได้มากขึ้น
แผนผังนั้นเรียกว่า กราฟคำนวณ (计算图, computational graph)
ขอยกฟังก์ชันง่ายๆขึ้นมาเพื่อแสดงตัวอย่างการเขียนกราฟคำนวณ เช่น ค่า h ขึ้นอยู่กับตัวแปรต้น a,b,c,d ดังนี้
..(5.1)
เราอาจเขียนการคำนวณเป็นลำดับขั้นได้ดังนี้
..(5.2)
เมื่อวาดเป็นกราฟคำนวณจะได้แบบนี้
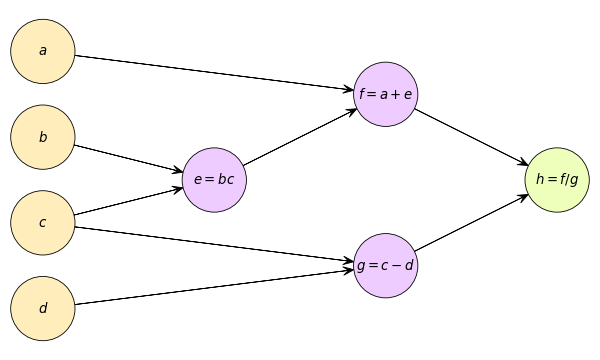
จะเห็นว่าในขณะที่เราคำนวณเพื่อหาค่าตัวสุดท้ายนั้น เราต้องผ่านการคำนวณค่าต่างๆตามลำดับขั้น เป็นคำนวรไปข้างหน้า
สมมุติให้ค่าของตัวแปรต้นเป็น a=1,b=2,c=3,d=4 การคำนวณจะเป็นแบบนี้
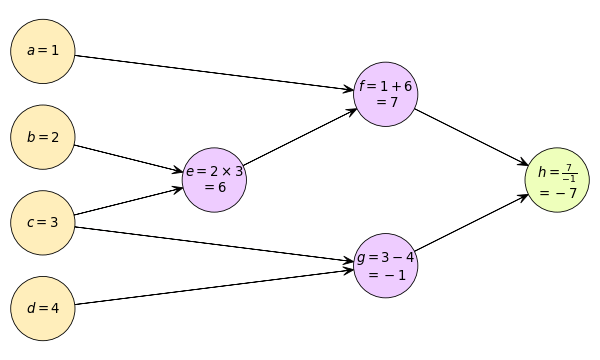
การแพร่ย้อนกลับ
ในขณะเดียวกัน กราฟคำนวณก็ทำให้เรามองเห็นความสัมพันธ์ต่างๆเพื่อคำนวณอนุพันธ์ตามกฎลูกโซ่ได้ง่าย
ให้ h เป็นจุดเริ่มต้น หาอนุพันธ์เทียบ f และ g แล้วก็โยงต่อไปเรื่อยๆจนถึง a,b,c,d
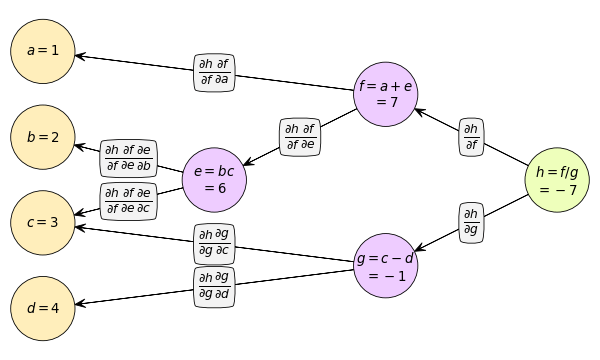
จะได้
..(5.3)
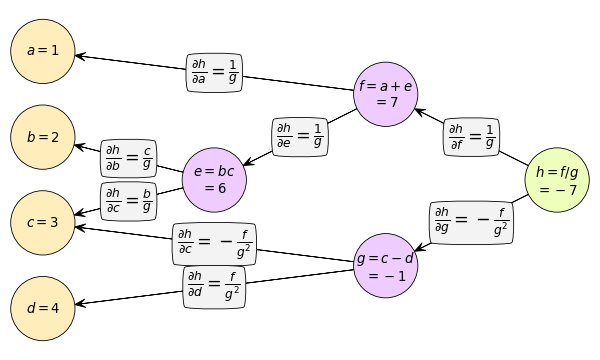
สำหรับ c นั้นขาไปเดิน ๒ สาย ตอนแพร่กลับก็จะต้องเอา ๒ สายนั้นมาบวกกันด้วย
และเราจะเห็นว่าค่าอนุพันธ์ของตัวแปรต้นจะมีส่วนที่ขึ้นกับค่าตัวแปรที่อยู่ระหว่างทางอย่าง f หรือ g ด้วย ซึ่งค่าเหล่านี้ก็ได้มาตั้งแต่ตอนที่คำนวณไปข้างหน้าเพื่อหาค่า h สามารถนำมาคำนวณค่าได้เลย
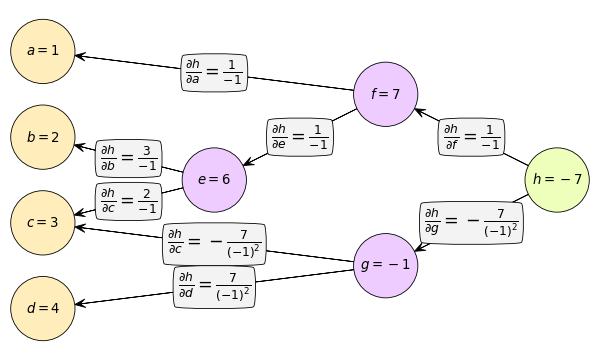
หมายความว่าหากเราจะหาอนุพันธ์เทียบกับตัวแปรต้นจะต้องผ่านการคำนวณไปข้างหน้าจนถึงขั้นเกือบท้ายสุด
ดังนั้นการคำนวณหาค่าตัวแปรปลายทางสุด นอกจากจะทำให้เราได้ค่าตัวแปรนั้น มันยังทำให้เราได้ค่าระหว่างทางซึ่งจะนำมาใช้คำนวณหาค่าอนุพันธ์ระหว่างตัวแปรนั้นกับตัวแปรต้นต่างๆได้ในตอนหลังด้วย
ยิงหินนัดเดียวได้นกสองตัว 一石二鸟
การไล่คำนวณค่าอนุพันธ์เป็นลำดับขั้นจากกราฟคำนวณนี้เป็นเทคนิคที่ถูกเรียกว่าการแพร่ย้อนกลับ (反向传播, backpropagation)
เทคนิคนี้มีความสำคัญสำหรับโครงข่ายประสาทเทียม เพราะภายในโครงข่ายประสาทเทียมมีการคำนวณต่อเนื่องเป็นขั้นเป็นตอนโดยไล่จากข้อมูลขาเข้าไปยังขาออก
กราฟคำนวณของฟังก์ชัน
กราฟคำนวณอาจเพื่อแสดงลำดับการคำนวณภายในฟังก์ชัน ตัวอย่างเช่นฟังก์ชันซิกมอยด์เขียนได้ดังนี้
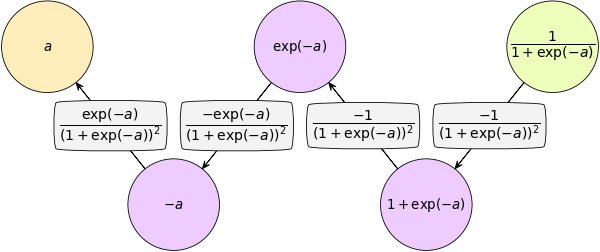
การคำนวณในฟังก์ชันไหนที่เรารู้อยู่แล้วและไม่ได้จำเป็นต้องแสดงรายละเอียดก็อาจเขียนยุบขั้นตอนไปเลย เขียนสั้นๆแบบนี้
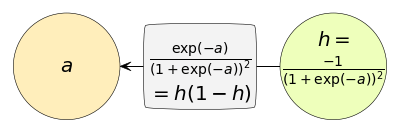
กราฟคำนวณของเพอร์เซปตรอนชั้นเดียว
คราวนี้มาดูตัวอย่างกราฟคำนวณจริงๆในโครงข่ายประสาทเทียมบ้าง กราฟคำนวณของเพอร์เซปตรอนที่ใช้ฟังก์ชันซิกมอยด์เป็นฟังก์ชันกระตุ้นอาจเขียนได้ดังนี้
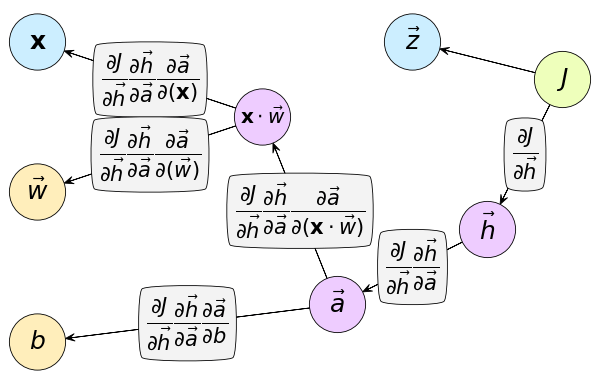
แทนค่าอนุพันธ์ต่างๆจากที่แสดงไว้ในบทที่แล้วลงไปได้
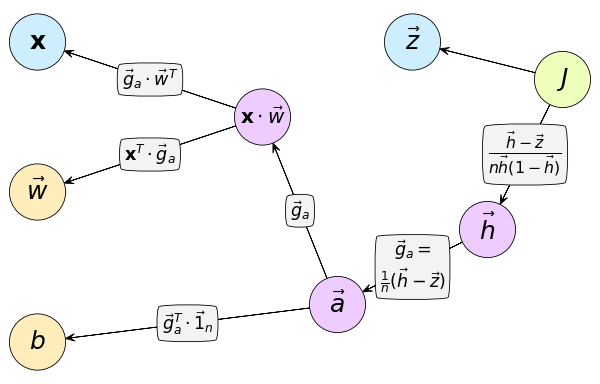
ในที่นี้ตัวแปรต้นของเราคือ x,w,b ส่วนตัวแปรปลายทางคือค่าเสียหาย J
h เป็นค่าที่คำนวณได้ระหว่างทาง และมันก็ถูกใช้ตอนที่หาอนุพันธ์ของ J เทียบกับ w และ b ด้วย
ทั้งหมดนี้คือตัวอย่างการวาดกราฟคำนวณซึ่งจะช่วยให้เห็นภาพรวมของการคำนวณโครงข่ายประสาทได้ดีขึ้น ต่อไปเมื่อเขียนโครงข่ายที่ซับซ้อนยิ่งขึ้นจะยิ่งเห็นประโยชน์
>> อ่านต่อ บทที่ ๖
กราฟคำนวณ
จะเห็นได้ว่ากว่าจะได้สูตรคำนวณความชันของฟังก์ชันค่าเสียหายเพื่อนำมาใช้คำนวณความเปลี่ยนแปลงของพารามิเตอร์ได้นั้นต้องผ่านการคำนวณด้วยกฎลูกโซ่ต่อเนื่องถึงสามครั้ง
ตรงนี้อาจยังดูเหมือนไม่มีปัญหาอะไรมาก แต่หากลงลึกไปในเนื้อหาการสร้างโครงข่ายประสาทเทียมเรื่อยๆสูตรคำนวณก็จะยิ่งซับซ้อนมากขึ้น
ดังนั้นก่อนที่จะไปต่อ ตรงนี้ขอแนะนำวิธีการเขียนแผนผังแสดงความสัมพันธ์ของตัวแปร ซึ่งจะช่วยให้เห็นภาพและเข้าใจการคำนวณภายในโครงข่ายประสาทเทียมได้มากขึ้น
แผนผังนั้นเรียกว่า กราฟคำนวณ (计算图, computational graph)
ขอยกฟังก์ชันง่ายๆขึ้นมาเพื่อแสดงตัวอย่างการเขียนกราฟคำนวณ เช่น ค่า h ขึ้นอยู่กับตัวแปรต้น a,b,c,d ดังนี้
..(5.1)
เราอาจเขียนการคำนวณเป็นลำดับขั้นได้ดังนี้
..(5.2)
เมื่อวาดเป็นกราฟคำนวณจะได้แบบนี้

จะเห็นว่าในขณะที่เราคำนวณเพื่อหาค่าตัวสุดท้ายนั้น เราต้องผ่านการคำนวณค่าต่างๆตามลำดับขั้น เป็นคำนวรไปข้างหน้า
สมมุติให้ค่าของตัวแปรต้นเป็น a=1,b=2,c=3,d=4 การคำนวณจะเป็นแบบนี้

การแพร่ย้อนกลับ
ในขณะเดียวกัน กราฟคำนวณก็ทำให้เรามองเห็นความสัมพันธ์ต่างๆเพื่อคำนวณอนุพันธ์ตามกฎลูกโซ่ได้ง่าย
ให้ h เป็นจุดเริ่มต้น หาอนุพันธ์เทียบ f และ g แล้วก็โยงต่อไปเรื่อยๆจนถึง a,b,c,d

จะได้
..(5.3)

สำหรับ c นั้นขาไปเดิน ๒ สาย ตอนแพร่กลับก็จะต้องเอา ๒ สายนั้นมาบวกกันด้วย
และเราจะเห็นว่าค่าอนุพันธ์ของตัวแปรต้นจะมีส่วนที่ขึ้นกับค่าตัวแปรที่อยู่ระหว่างทางอย่าง f หรือ g ด้วย ซึ่งค่าเหล่านี้ก็ได้มาตั้งแต่ตอนที่คำนวณไปข้างหน้าเพื่อหาค่า h สามารถนำมาคำนวณค่าได้เลย

หมายความว่าหากเราจะหาอนุพันธ์เทียบกับตัวแปรต้นจะต้องผ่านการคำนวณไปข้างหน้าจนถึงขั้นเกือบท้ายสุด
ดังนั้นการคำนวณหาค่าตัวแปรปลายทางสุด นอกจากจะทำให้เราได้ค่าตัวแปรนั้น มันยังทำให้เราได้ค่าระหว่างทางซึ่งจะนำมาใช้คำนวณหาค่าอนุพันธ์ระหว่างตัวแปรนั้นกับตัวแปรต้นต่างๆได้ในตอนหลังด้วย
ยิงหินนัดเดียวได้นกสองตัว 一石二鸟
การไล่คำนวณค่าอนุพันธ์เป็นลำดับขั้นจากกราฟคำนวณนี้เป็นเทคนิคที่ถูกเรียกว่าการแพร่ย้อนกลับ (反向传播, backpropagation)
เทคนิคนี้มีความสำคัญสำหรับโครงข่ายประสาทเทียม เพราะภายในโครงข่ายประสาทเทียมมีการคำนวณต่อเนื่องเป็นขั้นเป็นตอนโดยไล่จากข้อมูลขาเข้าไปยังขาออก
กราฟคำนวณของฟังก์ชัน
กราฟคำนวณอาจเพื่อแสดงลำดับการคำนวณภายในฟังก์ชัน ตัวอย่างเช่นฟังก์ชันซิกมอยด์เขียนได้ดังนี้

การคำนวณในฟังก์ชันไหนที่เรารู้อยู่แล้วและไม่ได้จำเป็นต้องแสดงรายละเอียดก็อาจเขียนยุบขั้นตอนไปเลย เขียนสั้นๆแบบนี้
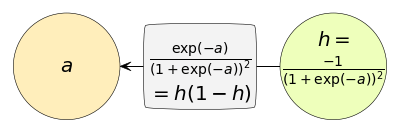
กราฟคำนวณของเพอร์เซปตรอนชั้นเดียว
คราวนี้มาดูตัวอย่างกราฟคำนวณจริงๆในโครงข่ายประสาทเทียมบ้าง กราฟคำนวณของเพอร์เซปตรอนที่ใช้ฟังก์ชันซิกมอยด์เป็นฟังก์ชันกระตุ้นอาจเขียนได้ดังนี้

แทนค่าอนุพันธ์ต่างๆจากที่แสดงไว้ในบทที่แล้วลงไปได้

ในที่นี้ตัวแปรต้นของเราคือ x,w,b ส่วนตัวแปรปลายทางคือค่าเสียหาย J
h เป็นค่าที่คำนวณได้ระหว่างทาง และมันก็ถูกใช้ตอนที่หาอนุพันธ์ของ J เทียบกับ w และ b ด้วย
ทั้งหมดนี้คือตัวอย่างการวาดกราฟคำนวณซึ่งจะช่วยให้เห็นภาพรวมของการคำนวณโครงข่ายประสาทได้ดีขึ้น ต่อไปเมื่อเขียนโครงข่ายที่ซับซ้อนยิ่งขึ้นจะยิ่งเห็นประโยชน์
>> อ่านต่อ บทที่ ๖
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy