โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๔: ปัญหาการวิเคราะห์การถดถอย
เขียนเมื่อ 2018/08/26 23:33
แก้ไขล่าสุด 2021/09/28 16:42
>> ต่อจาก บทที่ ๑๓
ในบทที่ผ่านๆมาเราพูดถึงแต่ปัญหาการจำแนกประเภทข้อมูล
ในบทนี้จะแสดงถึงตัวอย่างการใช้ในปัญหาวิเคราะห์การถดถอยบ้าง
การวิเคราะห์การถดถอยเชิงเส้น
การวิเคราะห์การถดถอย (回归, regression) คือการหาความสัมพันธ์ระหว่างตัวแปรต้นกับตัวแปรตาม
ตัวอย่างเช่น มีข้อมูลค่าตัวแปรต้น x และตัวแปรตาม z เขียนความสัมพันธ์ได้แบบนี้
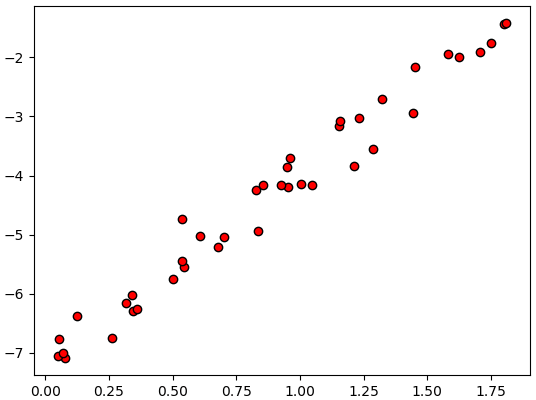
ความสัมพันธ์ดูแล้วมีแนวโน้มที่จะเป็นเส้นตรง ดังนั้นสามารถบอกความสัมพันธ์ระหว่าง x และ z ได้โดยการใช้เส้นตรงลากผ่าน ได้ความสัมพันธ์ z = xw+b แบบนี้เรียกว่าการวิเคราะห์การถดถอยเชิงเส้น (线性回归, linear regression)
เกี่ยวกับการวิเคราะห์การถดถอยเชิงเส้นนั้น เคยได้อธิบายละเอียดไปแล้วใน https://phyblas.hinaboshi.com/20161210
แต่ว่าในที่นี้จะลองมาเขียนการวิเคราะห์การถดถอยเชิงเส้นด้วยโครงข่ายประสาทเทียมที่อธิบายมาในบทก่อนๆ
ทั้งการวิเคราะห์การถดถอยและการวิเคราะห์จำแนกประเภทนั้นต่างก็เป็นการหาความสัมพันธ์ระหว่างตัวแปรต้นและตัวแปรตามเหมือนกัน แต่ต่างกันตรงที่ตัวแปรตามในการวิเคราะห์การจำแนกประเภทคือประเภทที่จำแนกได้ ส่วนการวิเคราะห์การถดถอยตัวแปรตามคือค่าตัวเลข
ในการวิเคราะห์การถดถอยเชิงเส้นนั้นเราอาจตั้งโครงข่ายประสาทในลักษณะเหมือนเพอร์เซปตรอนชั้นเดียวที่ใช้ในปัญหาการจำแนกประเภท (บทที่ ๓) แต่ต่างกันตรงที่ไม่ต้องใช้ฟังก์ชันกระตุ้นเลย ในขณะที่ในปัญหาการจำแนกประเภทนั้นเวลาหาคำนวณค่าเสียหายจะใช้ฟังก์ชันกระตุ้น คือฟังก์ชันซิกมอยด์หรือซอฟต์แม็กซ์ แล้วตามด้วยการหาค่าเอนโทรปีไขว้
แต่ว่าในการวิเคราะห์การถดถอยจะไม่มีการใช้ฟังก์ชันกระตุ้น และจะใช้ค่าความเสียหายเป็นค่าความต่างกำลังสองเฉลี่ย
..(14.1)
โดย z คือคำตอบจริง ส่วน h คือคำตอบที่คำนวณได้ จะเห็นว่ายิ่งต่างกันมากค่าก็ยิ่งมากแสดงว่ายิ่งไม่ดี จึงเป็นค่าที่จะต้องลด
h ก็มาจากการคำนวณจาก x และ w โดยตรง
..(14.2)
อนุพันธ์ของค่าเสียหายเทียบกับ w และ b ก็จะได้
..(14.3)
ต่อมาลองนิยามคลาสของชั้นค่าเสียหายนี้เหมือนกับที่ทำกับชั้นอื่นๆที่ผ่านมา
ก่อนอื่นนำเข้าคลาสต่างๆที่จำเป็นในบทนี้ ซึ่งเตรียมไว้ใน >> unagi.py
เราอาจเขียนชั้นของค่าความต่างกำลังสองเฉลี่ยได้ดังนี้
ต่อไปเป็นต้วอย่างการเขียนคลาสของการวิเคราะห์การถดถอยเชิงเส้น
ลองนำมาใช้กับข้อมูลหนึ่งมิติ
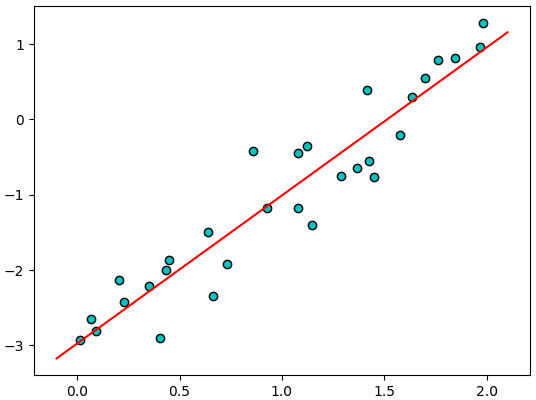
ลองใช้กับข้อมูลสองมิติ
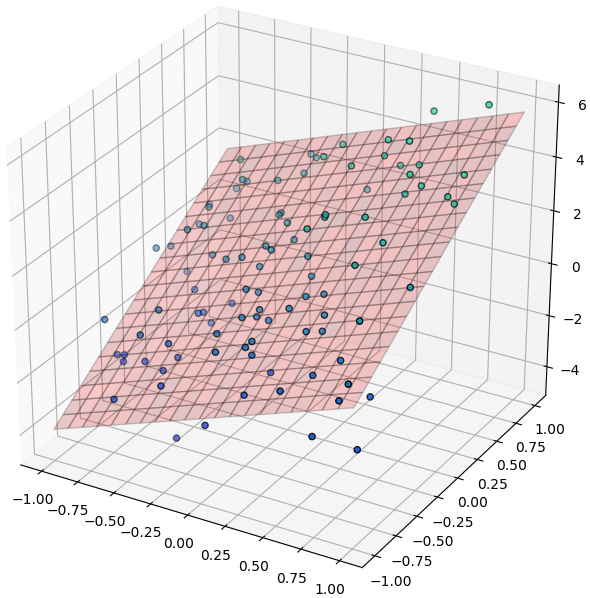
การวิเคราะห์การถดถอยแบบไม่เป็นเชิงเส้น
กรณีที่ความสัมพันธ์ดูมีแนวโน้มที่ไม่เป็นเชิงเส้น การถดถอยเชิงเส้นก็จะใช้ไม่ได้ และต้องใช้รูปแบบการคำนวณที่ซับซ้อนขึ้นไปกว่านั้น
ดังที่เคยกล่าวไว้ในบทที่ ๗ แล้วว่าเพื่อที่จะแก้ปัญหาที่ไม่เป็นเชิงเส้นจำเป็นต้องสร้างโครงข่ายประสาทที่ประกอบไปด้วยสองชั้นขึ้นไป ปัญหาการวิเคราะห์การถดถอยก็เช่นกัน
สำหรับปัญหาการวิเคราะห์การถดถอยนั้น แม้ว่าชั้นสุดท้ายจะไม่ต้องการฟังก์ชันกระตุ้น แต่ว่าในระหว่างชั้นต่างๆยังคงจำเป็นจะต้องใช้ฟังก์ชันกระตุ้นอยู่
ฟังก์ชันกระตุ้นระหว่างชั้นอาจเลือกใช้ ReLU หรือซิกมอยด์ก็ได้ แต่ผลที่ได้จะมีลักษณะค่อนข้างต่างกัน
ขอลองยกตัวอย่างเป็นโครงข่ายประสาท ๓ ชั้นที่ใช้ ReLU เขียนได้ดังนี้
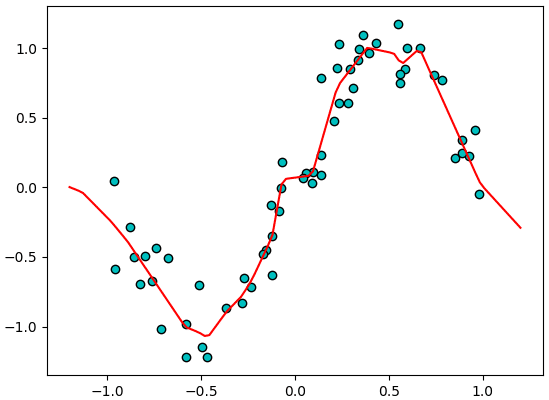
จะเห็นว่าดูแล้วกราฟพยายามจะเข้าไปผ่านจุดต่างๆ แต่ก็ดูไม่เป็นธรรมชาติ และเต็มไปด้วยเส้นตรง นี่เป็นผลของการใช้ ReLU เป็นฟังก์ชันกระตุ้น
คือแม้ว่า ReLU จะเป็นฟังก์ชันไม่เป็นเชิงเส้น แต่ก็แค่เป็นการนำเชิงเส้นมาหักเท่านั้น ยังไงโดยพื้นฐานก็ยังเป็นเชิงเส้น เมื่อใช้ ReLU เป็นฟังก์ชันกระตุ้นในการวิเคราะห์การถดถอยจึงได้ผลลัพธ์ที่เหมือนเส้นตรงหักเป็นช่วงๆ
ในขณะที่หากลองเปลี่ยนมาใช้ฟังก์ชันซิกมอยด์ดู
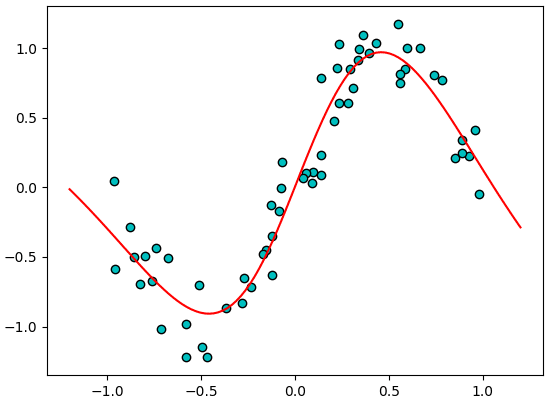
ผลที่ได้จะเห็นว่าเป็นเส้นโค้งดูเป็นธรรมชาติกว่า
>> อ่านต่อ บทที่ ๑๕
ในบทที่ผ่านๆมาเราพูดถึงแต่ปัญหาการจำแนกประเภทข้อมูล
ในบทนี้จะแสดงถึงตัวอย่างการใช้ในปัญหาวิเคราะห์การถดถอยบ้าง
การวิเคราะห์การถดถอยเชิงเส้น
การวิเคราะห์การถดถอย (回归, regression) คือการหาความสัมพันธ์ระหว่างตัวแปรต้นกับตัวแปรตาม
ตัวอย่างเช่น มีข้อมูลค่าตัวแปรต้น x และตัวแปรตาม z เขียนความสัมพันธ์ได้แบบนี้
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(0,2,40)
z = 3*x-7 + np.random.normal(0,0.3,40)
plt.scatter(x,z,c='r',edgecolor='k')
plt.show()
ความสัมพันธ์ดูแล้วมีแนวโน้มที่จะเป็นเส้นตรง ดังนั้นสามารถบอกความสัมพันธ์ระหว่าง x และ z ได้โดยการใช้เส้นตรงลากผ่าน ได้ความสัมพันธ์ z = xw+b แบบนี้เรียกว่าการวิเคราะห์การถดถอยเชิงเส้น (线性回归, linear regression)
เกี่ยวกับการวิเคราะห์การถดถอยเชิงเส้นนั้น เคยได้อธิบายละเอียดไปแล้วใน https://phyblas.hinaboshi.com/20161210
แต่ว่าในที่นี้จะลองมาเขียนการวิเคราะห์การถดถอยเชิงเส้นด้วยโครงข่ายประสาทเทียมที่อธิบายมาในบทก่อนๆ
ทั้งการวิเคราะห์การถดถอยและการวิเคราะห์จำแนกประเภทนั้นต่างก็เป็นการหาความสัมพันธ์ระหว่างตัวแปรต้นและตัวแปรตามเหมือนกัน แต่ต่างกันตรงที่ตัวแปรตามในการวิเคราะห์การจำแนกประเภทคือประเภทที่จำแนกได้ ส่วนการวิเคราะห์การถดถอยตัวแปรตามคือค่าตัวเลข
ในการวิเคราะห์การถดถอยเชิงเส้นนั้นเราอาจตั้งโครงข่ายประสาทในลักษณะเหมือนเพอร์เซปตรอนชั้นเดียวที่ใช้ในปัญหาการจำแนกประเภท (บทที่ ๓) แต่ต่างกันตรงที่ไม่ต้องใช้ฟังก์ชันกระตุ้นเลย ในขณะที่ในปัญหาการจำแนกประเภทนั้นเวลาหาคำนวณค่าเสียหายจะใช้ฟังก์ชันกระตุ้น คือฟังก์ชันซิกมอยด์หรือซอฟต์แม็กซ์ แล้วตามด้วยการหาค่าเอนโทรปีไขว้
แต่ว่าในการวิเคราะห์การถดถอยจะไม่มีการใช้ฟังก์ชันกระตุ้น และจะใช้ค่าความเสียหายเป็นค่าความต่างกำลังสองเฉลี่ย
..(14.1)
โดย z คือคำตอบจริง ส่วน h คือคำตอบที่คำนวณได้ จะเห็นว่ายิ่งต่างกันมากค่าก็ยิ่งมากแสดงว่ายิ่งไม่ดี จึงเป็นค่าที่จะต้องลด
h ก็มาจากการคำนวณจาก x และ w โดยตรง
..(14.2)
อนุพันธ์ของค่าเสียหายเทียบกับ w และ b ก็จะได้
..(14.3)
ต่อมาลองนิยามคลาสของชั้นค่าเสียหายนี้เหมือนกับที่ทำกับชั้นอื่นๆที่ผ่านมา
ก่อนอื่นนำเข้าคลาสต่างๆที่จำเป็นในบทนี้ ซึ่งเตรียมไว้ใน >> unagi.py
from unagi import Chan,Affin,Relu,Sigmoid,Adamเราอาจเขียนชั้นของค่าความต่างกำลังสองเฉลี่ยได้ดังนี้
class Mse(Chan):
def pai(self,h,z):
self.z = z[:,None]
self.h = h
return ((self.z-h)**2).mean()
def yon(self,g):
return g*2*(self.h-self.z)/len(self.z)ต่อไปเป็นต้วอย่างการเขียนคลาสของการวิเคราะห์การถดถอยเชิงเส้น
class ThotthoiChoengsen:
def rianru(self,X,z,n_thamsam):
self.chan = [Affin(X.shape[1],1,0),Mse()]
self.opt = Adam(self.chan[0].param)
for o in range(n_thamsam):
h = self.chan[0](X)
mse = self.chan[1](h,z)
mse.phraeyon()
self.opt()
def thamnai(self,X):
h = self.chan[0].pai(X)
return h.ravel()ลองนำมาใช้กับข้อมูลหนึ่งมิติ
x = np.random.uniform(0,2,30)
X = x[:,None]
z = 2*x-3 + np.random.normal(0,0.4,30)
tc = ThotthoiChoengsen()
tc.rianru(X,z,10000)
x_ = np.linspace(-0.1,2.1,101)
X_ = x_[:,None]
z_ = tc.thamnai(X_)
plt.scatter(x,z,c='c',edgecolor='k')
plt.plot(x_,z_,'r')
plt.show()
ลองใช้กับข้อมูลสองมิติ
from mpl_toolkits.mplot3d import Axes3D
X = np.random.uniform(-1,1,[100,2])
x,y = X.T
z = np.random.normal(x*2+y*3+1,1)
tc = ThotthoiChoengsen()
tc.rianru(X,z,10000)
plt.figure(figsize=[7,7])
ax = plt.axes([0,0,1,1],projection='3d')
ax.scatter(x,y,z,c=z,edgecolor='k',cmap='winter')
mx,my = np.meshgrid(np.linspace(-1,1,21),np.linspace(-1,1,21))
mX = np.array([mx.ravel(),my.ravel()]).T
mz = tc.thamnai(mX).reshape(21,-1)
ax.plot_surface(mx,my,mz,rstride=1,cstride=1,alpha=0.2,color='r',edgecolor='k')
plt.show()
การวิเคราะห์การถดถอยแบบไม่เป็นเชิงเส้น
กรณีที่ความสัมพันธ์ดูมีแนวโน้มที่ไม่เป็นเชิงเส้น การถดถอยเชิงเส้นก็จะใช้ไม่ได้ และต้องใช้รูปแบบการคำนวณที่ซับซ้อนขึ้นไปกว่านั้น
ดังที่เคยกล่าวไว้ในบทที่ ๗ แล้วว่าเพื่อที่จะแก้ปัญหาที่ไม่เป็นเชิงเส้นจำเป็นต้องสร้างโครงข่ายประสาทที่ประกอบไปด้วยสองชั้นขึ้นไป ปัญหาการวิเคราะห์การถดถอยก็เช่นกัน
สำหรับปัญหาการวิเคราะห์การถดถอยนั้น แม้ว่าชั้นสุดท้ายจะไม่ต้องการฟังก์ชันกระตุ้น แต่ว่าในระหว่างชั้นต่างๆยังคงจำเป็นจะต้องใช้ฟังก์ชันกระตุ้นอยู่
ฟังก์ชันกระตุ้นระหว่างชั้นอาจเลือกใช้ ReLU หรือซิกมอยด์ก็ได้ แต่ผลที่ได้จะมีลักษณะค่อนข้างต่างกัน
ขอลองยกตัวอย่างเป็นโครงข่ายประสาท ๓ ชั้นที่ใช้ ReLU เขียนได้ดังนี้
class PrasatThotthoi:
def __init__(self,m1,m2,eta=0.001):
self.m1 = m1
self.m2 = m2
self.eta = eta
self.chan = [None,
Relu(),
Affin(m1,m2,np.sqrt(2./m1)),
Relu(),
Affin(m2,1,0),
Mse()]
def rianru(self,X,z,n_thamsam):
m0 = X.shape[1]
self.chan[0] = Affin(m0,self.m1,np.sqrt(2./m0))
self.opt = Adam(self.param(),eta=self.eta)
for o in range(n_thamsam):
mse = self.ha_mse(X,z)
mse.phraeyon()
self.opt()
def ha_mse(self,X,z):
for c in self.chan[:-1]:
X = c(X)
return self.chan[-1](X,z)
def param(self):
p = []
for c in self.chan:
if(hasattr(c,'param')):
p.extend(c.param)
return p
def thamnai(self,X):
for c in self.chan[:-1]:
X = c(X)
return X.kha.ravel()
np.random.seed(0)
x = np.random.uniform(-1,1,60)
X = x[:,None]
z = np.sin(x*3)+np.random.normal(0,0.2,60)
m1,m2 = 20,30
ps = PrasatThotthoi(m1,m2,eta=0.005)
ps.rianru(X,z,1000)
x_ = np.linspace(-1.2,1.2,101)
X_ = x_[:,None]
z_ = ps.thamnai(X_)
plt.scatter(x,z,c='c',edgecolor='k')
plt.plot(x_,z_,'r')
plt.show()
จะเห็นว่าดูแล้วกราฟพยายามจะเข้าไปผ่านจุดต่างๆ แต่ก็ดูไม่เป็นธรรมชาติ และเต็มไปด้วยเส้นตรง นี่เป็นผลของการใช้ ReLU เป็นฟังก์ชันกระตุ้น
คือแม้ว่า ReLU จะเป็นฟังก์ชันไม่เป็นเชิงเส้น แต่ก็แค่เป็นการนำเชิงเส้นมาหักเท่านั้น ยังไงโดยพื้นฐานก็ยังเป็นเชิงเส้น เมื่อใช้ ReLU เป็นฟังก์ชันกระตุ้นในการวิเคราะห์การถดถอยจึงได้ผลลัพธ์ที่เหมือนเส้นตรงหักเป็นช่วงๆ
ในขณะที่หากลองเปลี่ยนมาใช้ฟังก์ชันซิกมอยด์ดู

ผลที่ได้จะเห็นว่าเป็นเส้นโค้งดูเป็นธรรมชาติกว่า
>> อ่านต่อ บทที่ ๑๕
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy