โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๗: การป้องกันการเรียนรู้เกินด้วยดรอปเอาต์
เขียนเมื่อ 2018/08/30 19:41
แก้ไขล่าสุด 2021/09/28 16:42
>> ต่อจาก บทที่ ๑๖
ในบทที่แล้วได้กล่าวถึงปัญหาการเรียนรู้เกิน (过学习, overlearning) ไปแล้ว
บทนี้จะพูดถึงวิธีการดรอปเอาต์ (dropout) ซึ่งนิยมใช้ในการลดปัญหาการเรียนรู้เกินของโครงข่ายประสาทเทียม
ดรอปเอาต์ คือการสร้างชั้นกรองชั้นหนึ่งสำหรับสุ่มเลือกให้ข้อมูลจากเซลล์ประสาทแค่บางเซลล์เท่านั้นผ่านไปได้
ตัวอย่างภาพแสดงการไหลของข้อมูล กรณีที่ดรอปเอาต์ของแต่ละชั้นเป็น 0.5 คือสุ่มตัดไปครึ่งนึง
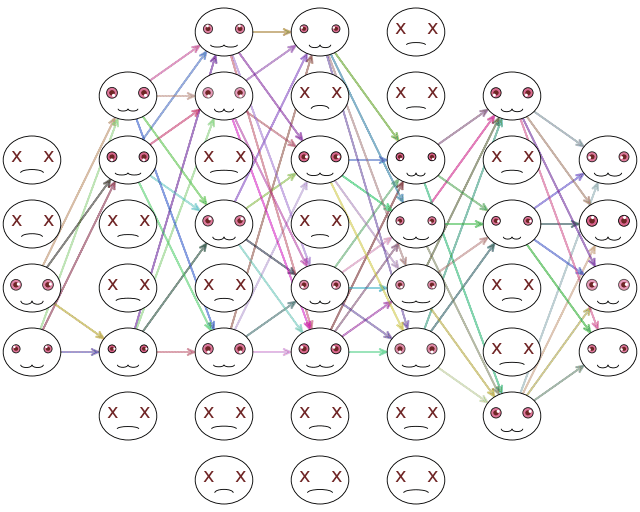
แต่ละรอบจะสุ่มไม่เหมือนกัน รอบต่อไปอาจไหลแบบนี้
ในแต่ละรอบของการฝึกเรียนรู้จะสุ่มเลือกไม่ซ้ำกัน ทำให้แต่ละรอบโครงข่ายใช้คนละเซลล์กันในการคำนวณ โดยรวมแล้วทุกเซลล์ก็ยังจะได้รับการฝึกอย่างทั่วถึง
เพียงแต่ว่าการสุ่มเอาเซลล์ออกนี้จะทำเฉพาะตอนที่กำลังฝึกแบบจำลองอยู่เท่านั้น แต่ตอนที่ใช้งานเพื่อทำการทำนายจริงๆจะเปิดใช้หมดทุกเซลล์พร้อมกัน
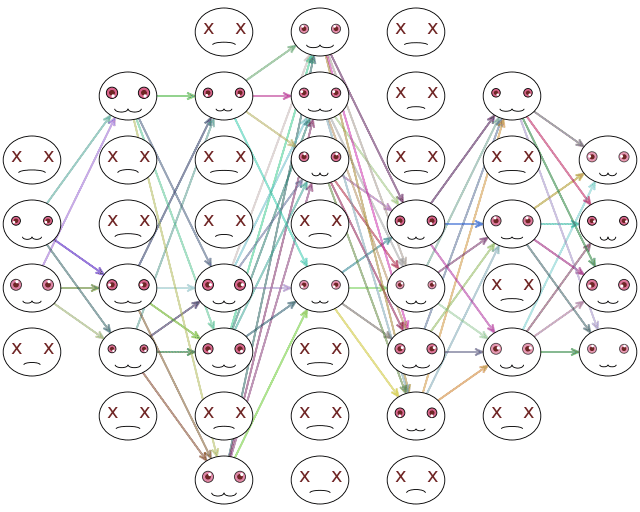
ชั้นดรอปเอาต์จะวางไว้ที่ก่อนหรือหลังชั้นฟังก์ชันกระตุ้นในแต่ละชั้นก็ได้
ตัวอย่างผังโครงสร้างเพอร์เซปตรอน ๔ ชั้นเมื่อวางดรอปเอาต์ไว้ก่อนฟังก์ชันกระตุ้น

แล้วทำไมวิธีการแบบนี้ถึงป้องกันการเรียนรู้เกินได้?
เพราะสาเหตุของการเรียนรู้เกินนั้นเกิดจากการที่ตัดสินอะไรแบบสุดขั้วไปจากข้อมูลด้านหนึ่งมากเกินไป
การสร้างดรอปเอาต์เป็นการเปิดโอกาสให้แต่ละรอบที่ทำการคำนวณนั้นข้อมูลถูกคำนวณด้วยเซลล์ที่ต่างกันไปตลอด แต่ละเซลล์นั้นทำหน้าที่คิดในคนละด้านต่างๆไม่ซ้ำกัน ทำให้ในแต่ละรอบเป็นการพิจารณาปัญหาด้วยมุมมองที่ต่างกันไป แต่ไม่ว่าจะพิจารณาแบบไหนก็จะต้องมุ่งสู่คำตอบแบบเดียวกัน
และเมื่อถึงคราวใช้งานจริง เซลล์ทั้งหมดจะถูกนำมาใช้ ทำให้วิธีการพิจารณาปัญหาทั้งหมดทุกรูปแบบถูกนำมาใช้พร้อมกัน ผลลัพธ์จึงออกมามีประสิทธิภาพ
ที่จริงแล้วแนวคิดของดรอปเอาต์นั้นเหมือนกับเทคนิคที่เรียกว่าการเรียนรู้แบบอ็องซ็องบล์ (集成学习, ensemble learning) ซึ่งเป็นวิธีการที่สร้างแบบจำลองสำหรับทำนายขึ้นมาหลายๆตัวแล้วให้เรียนรู้ข้อมูลเดียวกัน แล้วสุดท้ายเวลาทำนายก็เอาแบบจำลองเหล่านี้มาพิจารณาร่วมกัน ซึ่งจะได้ประสิทธิภาพมากกว่าการพิจารณาด้วยแบบจำลองตัวเดียว
สำหรับโครงข่ายประสาทเทียม แค่สร้างชั้นดรอปเอาต์ขึ้นก็มีผลเทียบเท่ากับการเรียนรู้แบบอ็องซ็องบล์แล้ว นี่เป็นการอาศัยประโยชน์จากการที่โครงข่ายประสาทเทียมประกอบด้วยเซลล์จำนวนมาก แต่ละเซลล์ก็ทำหน้าพิจารณาต่างกันเสมือนกับการสร้างแบบจำลองขึ้นหลายแบบในการเรียนรู้แบบอ็องซ็องบล์
เราจะทำการสร้างคลาสของชั้นดรอปเอาต์ขึ้นในลักษณะเดียวกันกับชั้นของฟังก์ชันกระตุ้นซึ่งสร้างมาในบทก่อนๆ
แต่ว่ามีสิ่งที่จะต่างกันไปซึ่งต้องระวังก็คือ ชั้นของดรอปเอาต์จะต้องมีการแยกกรณีระหว่างตอนที่ฝึกกับตอนที่ใช้งานจริง เพราะตอนที่ฝึกจะให้ข้อมูลผ่านแค่บางส่วน แต่ตอนใช้งานจริงจะให้ไหลทั้งหมด
ดังนั้นเราจะทำการเพิ่มแอตทริบิวต์ให้กับชั้นเพื่อแสดงว่ากำลังฝึกอยู่หรือไม่ เพื่อจะแยกกรณี
ก่อนอื่น ให้ทำการดึงคลาสที่จำเป็นต้องใช้ในบทนี้จาก unagi.py
ชั้นดรอปเอาต์อาจนิยามดังนี้
ค่า .fuekyu มีไว้แบ่งกรณีว่ากำลังอยู่ในโหมดฝึกอยู่หรือเปล่า ถ้าฝึกอยู่จะมีค่าเป็น 1 และจะมีการกรองเพื่อตัดค่าขาเข้าส่วนหนึ่งทิ้งไป ถ้าไม่ได้ฝึกอยู่ก็จะมีค่าเป็น 0 ก็จะไม่มีการกรองแต่ปล่อยให้ค่าทั้งหมดไหลผ่านไป
แต่ว่าการที่มีการกรองตัดค่าส่วนหนึ่งทิ้งไปนั้นย่อมทำให้ค่าที่ไหลผ่านลดลงกว่าเวลาที่ไม่มีการกรอง ดังนั้นเมื่อไม่กรองจำเป็นต้องคูณกับสัดส่วนการดรอปเอาต์ด้วย เพื่อให้ค่าที่ได้ออกมาเท่ากัน
หรือจะทำในทางตรงกันข้ามก็ได้ คือให้ค่าเวลาฝึกมีค่าเพิ่มขึ้นเพื่อชดเชยส่วนที่ถูกกรองทิ้งไป แล้วให้เวลาที่ไม่มีการกรองมีค่าไหลผ่านไปตามปกติ
จะทำแบบไหนผลก็ไม่ต่างกันนัก
ที่สำคัญคือ อย่าลืมปรับโหมดให้ถูกต้อง คือตอนฝึกให้ตั้ง .fuekyu=1 แต่พอจะใช้ทดสอบทำนายจริงให้ตั้ง .fuekyu=0
ต่อไปเป็นตัวอย่างการนำมาใช้ เราอาจสร้างคลาสโครงข่ายประสาทเทียมโดยใส่ดรอปเอาต์ด้วยได้ในลักษณะแบบนี้
เมธอด .ha_entropy() ใช้คำนวนไปข้างหน้าในตอนฝึก จึงมีการปรับโหมดให้เป็นโหมดฝึก fuekyu=1
พอทำแบบนี้ค่า .fuekyu นี้จะถูกป้อนให้กับทุกชั้น แต่สำหรับชั้นอื่นนอกจากชั้นดรอปเอาต์แล้วไม่ได้มีผลอะไร
ส่วนเมธอด .thamnai() สำหรับใช้ทำนายผลนั้นตั้งให้ปกติเป็น fuekyu=0 เพราะเป็นการใช้งานจริง
ลองนำมาใช้เพื่อวิเคราะห์ข้อมูลรูปร่างต่างๆเช่นเดียวกับบทที่แล้ว >> https://phyblas.hinaboshi.com/triamhai/ruprang-raisi-25x25x1000x5.rar
เพื่อให้เห็นปัญหาเรื่องการเรียนรู้เกินชัดเจนคราวนี้จะใช้ข้อมูลแค่ 1/10 ของทั้งหมด คือแค่ 500 รูปเท่านั้น โดยแบ่ง 400 รูปเป็นข้อมูลฝึก ส่วนอีก 100 รูปเป็นข้อมูลตรวจสอบ
เปรียบเทียบผลระหว่างมีดรอปเอาต์ใส่อยู่ในแต่ละชั้นโดยมีอัตราดรอปเป็น 0.2 กับไม่มีดรอปเอาต์
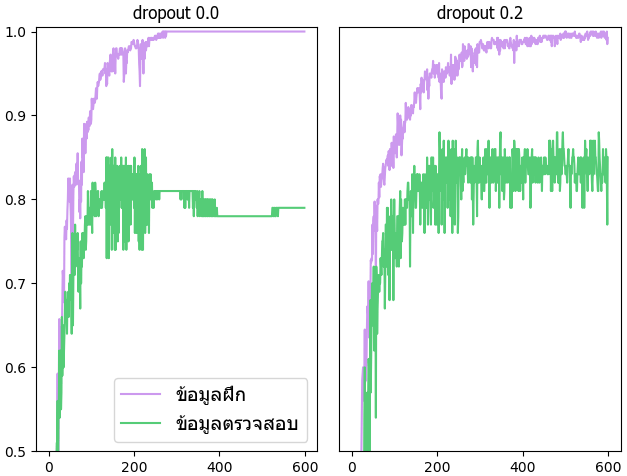
จะเห็นว่าเมื่อไม่มีดรอปเอาต์แล้วความแม่นในการทำนายข้อมูลฝึกเพิ่มขึ้นอย่างรวดเร็วจนแทบเต็ม 100% ในขณะที่ความแม่นสำหรับข้อมูลตรวจสอบไม่ได้เพิ่มขนาดนั้น แต่พอมีดรอปเอาต์แล้วความแตกต่างระหว่างข้อมูลฝึกและข้อมูลตรวจสอบก็ลดลง
อาจลองปรับแบบจำลองโดยเปลี่ยนอัตราดรอปหรือจำนวนชั้นแล้วลองใหม่ดูได้
>> อ่านต่อ บทที่ ๑๘
ในบทที่แล้วได้กล่าวถึงปัญหาการเรียนรู้เกิน (过学习, overlearning) ไปแล้ว
บทนี้จะพูดถึงวิธีการดรอปเอาต์ (dropout) ซึ่งนิยมใช้ในการลดปัญหาการเรียนรู้เกินของโครงข่ายประสาทเทียม
ดรอปเอาต์ คือการสร้างชั้นกรองชั้นหนึ่งสำหรับสุ่มเลือกให้ข้อมูลจากเซลล์ประสาทแค่บางเซลล์เท่านั้นผ่านไปได้
ตัวอย่างภาพแสดงการไหลของข้อมูล กรณีที่ดรอปเอาต์ของแต่ละชั้นเป็น 0.5 คือสุ่มตัดไปครึ่งนึง

แต่ละรอบจะสุ่มไม่เหมือนกัน รอบต่อไปอาจไหลแบบนี้

ในแต่ละรอบของการฝึกเรียนรู้จะสุ่มเลือกไม่ซ้ำกัน ทำให้แต่ละรอบโครงข่ายใช้คนละเซลล์กันในการคำนวณ โดยรวมแล้วทุกเซลล์ก็ยังจะได้รับการฝึกอย่างทั่วถึง
เพียงแต่ว่าการสุ่มเอาเซลล์ออกนี้จะทำเฉพาะตอนที่กำลังฝึกแบบจำลองอยู่เท่านั้น แต่ตอนที่ใช้งานเพื่อทำการทำนายจริงๆจะเปิดใช้หมดทุกเซลล์พร้อมกัน
ชั้นดรอปเอาต์จะวางไว้ที่ก่อนหรือหลังชั้นฟังก์ชันกระตุ้นในแต่ละชั้นก็ได้
ตัวอย่างผังโครงสร้างเพอร์เซปตรอน ๔ ชั้นเมื่อวางดรอปเอาต์ไว้ก่อนฟังก์ชันกระตุ้น

แล้วทำไมวิธีการแบบนี้ถึงป้องกันการเรียนรู้เกินได้?
เพราะสาเหตุของการเรียนรู้เกินนั้นเกิดจากการที่ตัดสินอะไรแบบสุดขั้วไปจากข้อมูลด้านหนึ่งมากเกินไป
การสร้างดรอปเอาต์เป็นการเปิดโอกาสให้แต่ละรอบที่ทำการคำนวณนั้นข้อมูลถูกคำนวณด้วยเซลล์ที่ต่างกันไปตลอด แต่ละเซลล์นั้นทำหน้าที่คิดในคนละด้านต่างๆไม่ซ้ำกัน ทำให้ในแต่ละรอบเป็นการพิจารณาปัญหาด้วยมุมมองที่ต่างกันไป แต่ไม่ว่าจะพิจารณาแบบไหนก็จะต้องมุ่งสู่คำตอบแบบเดียวกัน
และเมื่อถึงคราวใช้งานจริง เซลล์ทั้งหมดจะถูกนำมาใช้ ทำให้วิธีการพิจารณาปัญหาทั้งหมดทุกรูปแบบถูกนำมาใช้พร้อมกัน ผลลัพธ์จึงออกมามีประสิทธิภาพ
ที่จริงแล้วแนวคิดของดรอปเอาต์นั้นเหมือนกับเทคนิคที่เรียกว่าการเรียนรู้แบบอ็องซ็องบล์ (集成学习, ensemble learning) ซึ่งเป็นวิธีการที่สร้างแบบจำลองสำหรับทำนายขึ้นมาหลายๆตัวแล้วให้เรียนรู้ข้อมูลเดียวกัน แล้วสุดท้ายเวลาทำนายก็เอาแบบจำลองเหล่านี้มาพิจารณาร่วมกัน ซึ่งจะได้ประสิทธิภาพมากกว่าการพิจารณาด้วยแบบจำลองตัวเดียว
สำหรับโครงข่ายประสาทเทียม แค่สร้างชั้นดรอปเอาต์ขึ้นก็มีผลเทียบเท่ากับการเรียนรู้แบบอ็องซ็องบล์แล้ว นี่เป็นการอาศัยประโยชน์จากการที่โครงข่ายประสาทเทียมประกอบด้วยเซลล์จำนวนมาก แต่ละเซลล์ก็ทำหน้าพิจารณาต่างกันเสมือนกับการสร้างแบบจำลองขึ้นหลายแบบในการเรียนรู้แบบอ็องซ็องบล์
เราจะทำการสร้างคลาสของชั้นดรอปเอาต์ขึ้นในลักษณะเดียวกันกับชั้นของฟังก์ชันกระตุ้นซึ่งสร้างมาในบทก่อนๆ
แต่ว่ามีสิ่งที่จะต่างกันไปซึ่งต้องระวังก็คือ ชั้นของดรอปเอาต์จะต้องมีการแยกกรณีระหว่างตอนที่ฝึกกับตอนที่ใช้งานจริง เพราะตอนที่ฝึกจะให้ข้อมูลผ่านแค่บางส่วน แต่ตอนใช้งานจริงจะให้ไหลทั้งหมด
ดังนั้นเราจะทำการเพิ่มแอตทริบิวต์ให้กับชั้นเพื่อแสดงว่ากำลังฝึกอยู่หรือไม่ เพื่อจะแยกกรณี
ก่อนอื่น ให้ทำการดึงคลาสที่จำเป็นต้องใช้ในบทนี้จาก unagi.py
from unagi import Chan,ha_1h,Affin,Relu,Softmax_entropy,Adamชั้นดรอปเอาต์อาจนิยามดังนี้
import numpy as np
class Dropout(Chan):
def __init__(self,drop=0.5):
self.drop = drop
self.fuekyu = 1
def pai(self,x):
if(self.fuekyu):
self.krong = np.random.rand(*x.shape)>self.drop
return x*self.krong
else:
return x*(1.-self.drop)
def yon(self,g):
return g*self.krongค่า .fuekyu มีไว้แบ่งกรณีว่ากำลังอยู่ในโหมดฝึกอยู่หรือเปล่า ถ้าฝึกอยู่จะมีค่าเป็น 1 และจะมีการกรองเพื่อตัดค่าขาเข้าส่วนหนึ่งทิ้งไป ถ้าไม่ได้ฝึกอยู่ก็จะมีค่าเป็น 0 ก็จะไม่มีการกรองแต่ปล่อยให้ค่าทั้งหมดไหลผ่านไป
แต่ว่าการที่มีการกรองตัดค่าส่วนหนึ่งทิ้งไปนั้นย่อมทำให้ค่าที่ไหลผ่านลดลงกว่าเวลาที่ไม่มีการกรอง ดังนั้นเมื่อไม่กรองจำเป็นต้องคูณกับสัดส่วนการดรอปเอาต์ด้วย เพื่อให้ค่าที่ได้ออกมาเท่ากัน
หรือจะทำในทางตรงกันข้ามก็ได้ คือให้ค่าเวลาฝึกมีค่าเพิ่มขึ้นเพื่อชดเชยส่วนที่ถูกกรองทิ้งไป แล้วให้เวลาที่ไม่มีการกรองมีค่าไหลผ่านไปตามปกติ
จะทำแบบไหนผลก็ไม่ต่างกันนัก
ที่สำคัญคือ อย่าลืมปรับโหมดให้ถูกต้อง คือตอนฝึกให้ตั้ง .fuekyu=1 แต่พอจะใช้ทดสอบทำนายจริงให้ตั้ง .fuekyu=0
ต่อไปเป็นตัวอย่างการนำมาใช้ เราอาจสร้างคลาสโครงข่ายประสาทเทียมโดยใส่ดรอปเอาต์ด้วยได้ในลักษณะแบบนี้
class Prasat:
def __init__(self,m,eta=0.001,drop=0):
self.m = m
self.chan = []
for i in range(len(m)-1):
self.chan.append(Affin(m[i],m[i+1],np.sqrt(2./m[i])))
if(i<len(m)-2):
if(drop): # ใส่ดรอปเอาต์ทุกชั้นยกเว้นชั้นสุดท้าย
self.chan.append(Dropout(drop))
self.chan.append(Relu())
self.chan.append(Softmax_entropy())
self.opt = Adam(self.param(),eta=eta)
def rianru(self,X,z,X_truat,z_truat,n_thamsam=100):
Z = ha_1h(z,self.m[-1])
self.khanaen_fuek = []
self.khanaen_truat = []
for o in range(n_thamsam):
entropy = self.ha_entropy(X,Z)
entropy.phraeyon()
self.opt()
khanaen_fuek = self.ha_khanaen(X,z)
khanaen_truat = self.ha_khanaen(X_truat,z_truat)
self.khanaen_fuek.append(khanaen_fuek)
self.khanaen_truat.append(khanaen_truat)
if(o%100==99):
print(u'ผ่านไป %d รอบ, ทำนายข้อมูลฝึกแม่น=%.2f, ทำนายข้อมูลตรวจสอบแม่น=%.2f'%(o+1,khanaen_fuek,khanaen_truat))
def ha_entropy(self,X,Z,fuekyu=1):
for c in self.chan[:-1]:
c.fuekyu = fuekyu
X = c(X)
return self.chan[-1](X,Z)
def param(self):
p = []
for c in self.chan:
if(hasattr(c,'param')):
p.extend(c.param)
return p
def thamnai(self,X,fuekyu=0):
for c in self.chan[:-1]:
c.fuekyu = fuekyu
X = c(X)
return X.kha.argmax(1)
def ha_khanaen(self,X,z):
return (self.thamnai(X)==z).mean()เมธอด .ha_entropy() ใช้คำนวนไปข้างหน้าในตอนฝึก จึงมีการปรับโหมดให้เป็นโหมดฝึก fuekyu=1
พอทำแบบนี้ค่า .fuekyu นี้จะถูกป้อนให้กับทุกชั้น แต่สำหรับชั้นอื่นนอกจากชั้นดรอปเอาต์แล้วไม่ได้มีผลอะไร
ส่วนเมธอด .thamnai() สำหรับใช้ทำนายผลนั้นตั้งให้ปกติเป็น fuekyu=0 เพราะเป็นการใช้งานจริง
ลองนำมาใช้เพื่อวิเคราะห์ข้อมูลรูปร่างต่างๆเช่นเดียวกับบทที่แล้ว >> https://phyblas.hinaboshi.com/triamhai/ruprang-raisi-25x25x1000x5.rar
เพื่อให้เห็นปัญหาเรื่องการเรียนรู้เกินชัดเจนคราวนี้จะใช้ข้อมูลแค่ 1/10 ของทั้งหมด คือแค่ 500 รูปเท่านั้น โดยแบ่ง 400 รูปเป็นข้อมูลฝึก ส่วนอีก 100 รูปเป็นข้อมูลตรวจสอบ
เปรียบเทียบผลระหว่างมีดรอปเอาต์ใส่อยู่ในแต่ละชั้นโดยมีอัตราดรอปเป็น 0.2 กับไม่มีดรอปเอาต์
import matplotlib.pyplot as plt
from glob import glob
# โหลดเฉพาะรูปที่ชื่อลงท้ายด้วยเลข 1 ซึ่งมีอยู่ 1/10 ของรูปทั้งหมด
X = np.array([plt.imread(x) for x in sorted(glob('ruprang-raisi-25x25x1000x5/*/*1.png'))])
X = X.reshape(-1,25*25)
z = np.arange(5).repeat(100)
n = len(z) # จำนวนข้อมูลทั้งหมด
n_fuek = int(n*0.8) # จำนวนข้อมูลฝึกเป็น 4 ใน 5
np.random.seed(9)
sumlueak = np.random.permutation(n)
X_fuek,X_truat = X[sumlueak[:n_fuek]],X[sumlueak[n_fuek:]]
z_fuek,z_truat = z[sumlueak[:n_fuek]],z[sumlueak[n_fuek:]]
plt.figure(figsize=[6.5,5])
for drop in [0,1]:
plt.subplot(1,2,1+drop,ylim=[0.5,1.005])
drop *= 0.2
prasat = Prasat(m=[625,100,100,100,6],drop=drop)
prasat.rianru(X_fuek,z_fuek,X_truat,z_truat,n_thamsam=600)
plt.plot(prasat.khanaen_fuek,'#cc99ee')
plt.plot(prasat.khanaen_truat,'#55cc77')
plt.title(u'dropout %.1f'%drop,family='Tahoma',size=12)
if(drop==0):
plt.legend([u'ข้อมูลฝึก',u'ข้อมูลตรวจสอบ'],prop={'family':'Tahoma','size':14})
else:
plt.yticks([])
plt.tight_layout()
plt.show()
จะเห็นว่าเมื่อไม่มีดรอปเอาต์แล้วความแม่นในการทำนายข้อมูลฝึกเพิ่มขึ้นอย่างรวดเร็วจนแทบเต็ม 100% ในขณะที่ความแม่นสำหรับข้อมูลตรวจสอบไม่ได้เพิ่มขนาดนั้น แต่พอมีดรอปเอาต์แล้วความแตกต่างระหว่างข้อมูลฝึกและข้อมูลตรวจสอบก็ลดลง
อาจลองปรับแบบจำลองโดยเปลี่ยนอัตราดรอปหรือจำนวนชั้นแล้วลองใหม่ดูได้
>> อ่านต่อ บทที่ ๑๘
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy