โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๙: ฟังก์ชันกระตุ้นแบบต่างๆ
เขียนเมื่อ 2018/09/04 19:07
แก้ไขล่าสุด 2022/07/10 21:08
>> ต่อจาก บทที่ ๑๘
ฟังก์ชันกระตุ้น (激活函数, activation function) เป็นส่วนประกอบที่สำคัญของโครงข่ายประสาทเทียม ใช้ทั้งแทรกระหว่างแต่ละชั้นเพื่อให้เกิดการคำนวณที่ไม่เป็นเชิงเส้น และใช้ทั้งในชั้นสุดท้ายก่อนคำนวณค่าเสียหายเพื่อจะทำการแพร่ย้อนกลับ
ที่ผ่านมาได้แนะนำฟังก์ชันกระตุ้นไปแค่ฟังก์ชันซิกมอยด์, ซอฟต์แม็กซ์ และ ReLU แต่จริงๆแล้วฟังก์ชันกระตุ้นมีหลากหลายรูปแบบมาก ถูกเลือกใช้ในสถานการณ์ต่างๆกันไป
คราวนี้จะมาลองแนะนำให้รู้จักกับฟังก์ชันกระตุ้นแบบอื่นๆซึ่งถูกใช้ระหว่างชั้นในโครงข่ายประสาทเทียม (เพื่อให้ได้เปรียบเทียบ ทั้งซิกมอยด์และ ReLU ก็จะเขียนสรุปในนี้ด้วย)
sigmoid
ฟังก์ชันกระตุ้นที่นิยมใช้กันมาช้านานตั้งแต่ยุคแรก
..(19.1)
นิยามคลาสได้ดังนี้ (คลาส Chan ให้นำเข้าจาก unagi.py เช่นเคย)
ขอสร้างฟังก์ชันขึ้นมาเพื่อสำหรับใช้วาดทั้งฟังก์ชันนี้และฟังก์ชันต่อไปด้วย และทำการวาดขึ้นมา

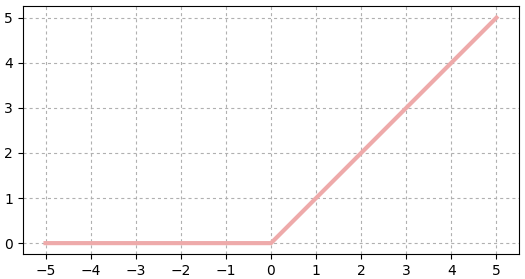
ReLU
ย่อมาจาก rectified linear unit
ถูกนำมาใช้ในโครงข่ายประสาทเทียมตั้งแต่ปี 2011 ด้วยโครงสร้างที่เรียบง่ายแต่กลับใช้ได้ผลดีจึงกลายเป็นฟังก์ชันกระตุ้นที่เป็นที่นิยมใช้ที่สุด
..(19.2)
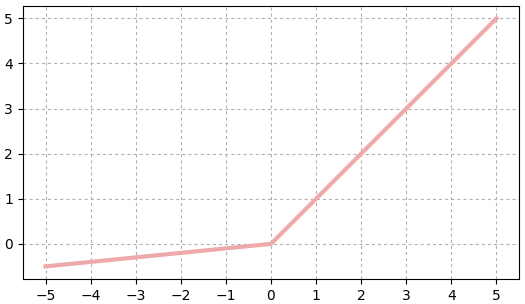
LReLU
ย่อมาจาก leaky rectified linear unit นิยามโดย
..(19.3)
คล้ายกับ ReLU แต่ว่าช่วงที่ต่ำกว่า 0 จะมีค่า โดยขึ้นกับค่า a ซึ่งเป็นค่าที่จะกำหนดเท่าไหร่ก็ได้ (ถ้า a=0 ก็จะกลายเป็น ReLU ธรรมดา)
PReLU
ย่อมาจาก parametric rectified linear unit นิยามโดย
..(19.4)
คล้ายกับ LReLU เพียงแต่ a ในที่นี้เป็นพารามิเตอร์ซึ่งมีจำนวนเท่ากับจำนวนตัวแปรในชั้นนั้น และต้องปรับค่าให้เหมาะสมไปในขณะเรียนรู้
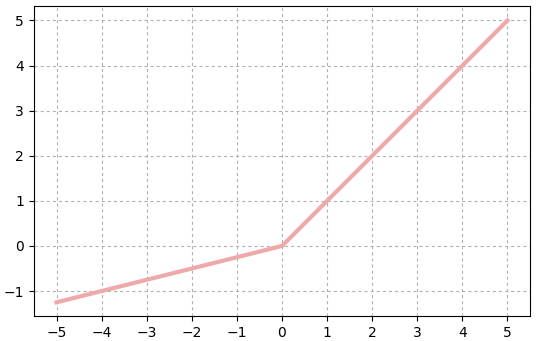
จะเห็นว่ามีพารามิเตอร์ที่ต้องเรียนรู้และปรับค่า ซึ่งต่างจากฟังก์ชันกระตุ้นทั่วๆไปชนิดอื่น
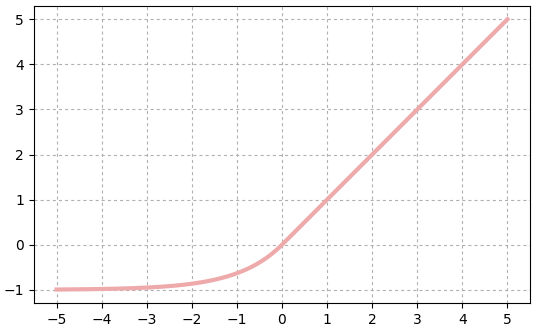
ELU
ย่อมาจาก exponential rectified linear unit
คล้าย ReLU แต่ครึ่งลบจะนิยามโดยเอกซ์โพเนนเชียล
..(19.5)
SELU
ย่อมาจาก scaled exponential rectified linear unit
คล้ายกับ ELU แต่มีการคูณ λ เข้าไปอีก
..(19.6)
โดยที่ λ และ a ในที่นี้เป็นค่าที่ถูกกำหนดตายตัว
λ = 1.0507009873554804934193349852946
a = 1.6732632423543772848170429916717
ค่านี้เป็นค่าปรับสเกลที่ได้จากการวิจัยแล้วพบว่าได้ผลออกมาลงตัวน่าพอใจ
tanh
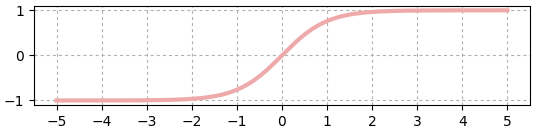
เป็นฟังก์ชันไฮเพอร์โบลิก ซึ่งมีหน้าตาคล้ายซิกมอยด์ เพียงแต่มีค่าอยู่ในช่วง -1 ถึง 1
..(19.7)
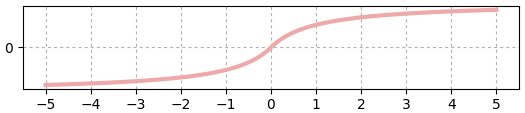
softsign
มีค่าอยู่ในช่วง -1 ถึง 1 คล้าย tanh
..(19.8)
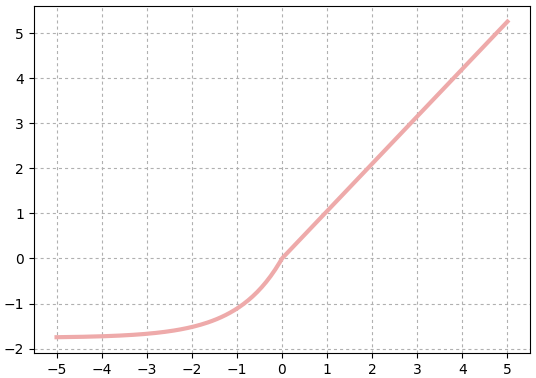
softplus
ที่ค่าไกลจาก 0 จะคล้าย ReLU แต่ที่ค่าใกล้ 0 จะเป็นเส้นโค้งแทนที่จะหักมุม
..(19.9)
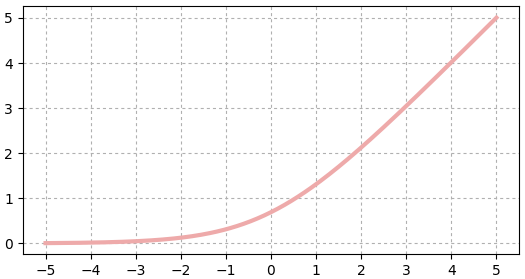
สุดท้ายลองวาดภาพรวมทั้งหมดเทียบกันดู
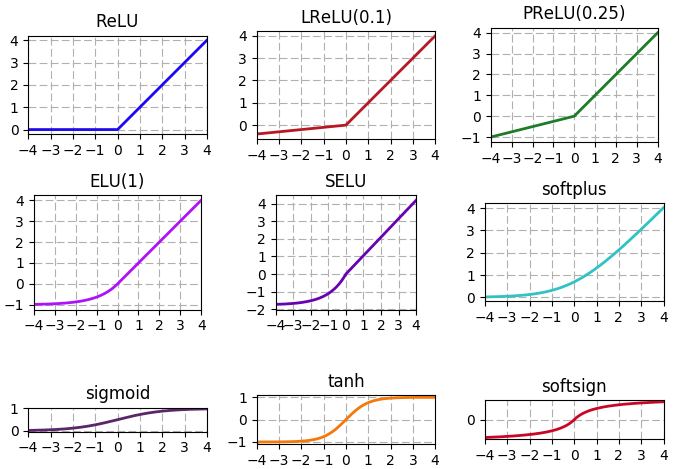
นอกจากนี้ก็ยังมีฟังก์ชันอื่นๆที่ไม่ได้แนะนำ และยังอาจมีฟังก์ชันใหม่ๆถูกคิดขึ้นมาและเป็นที่นิยมขึ้นมาอีกในอนาคต
>> อ่านต่อ บทที่ ๒๐
ฟังก์ชันกระตุ้น (激活函数, activation function) เป็นส่วนประกอบที่สำคัญของโครงข่ายประสาทเทียม ใช้ทั้งแทรกระหว่างแต่ละชั้นเพื่อให้เกิดการคำนวณที่ไม่เป็นเชิงเส้น และใช้ทั้งในชั้นสุดท้ายก่อนคำนวณค่าเสียหายเพื่อจะทำการแพร่ย้อนกลับ
ที่ผ่านมาได้แนะนำฟังก์ชันกระตุ้นไปแค่ฟังก์ชันซิกมอยด์, ซอฟต์แม็กซ์ และ ReLU แต่จริงๆแล้วฟังก์ชันกระตุ้นมีหลากหลายรูปแบบมาก ถูกเลือกใช้ในสถานการณ์ต่างๆกันไป
คราวนี้จะมาลองแนะนำให้รู้จักกับฟังก์ชันกระตุ้นแบบอื่นๆซึ่งถูกใช้ระหว่างชั้นในโครงข่ายประสาทเทียม (เพื่อให้ได้เปรียบเทียบ ทั้งซิกมอยด์และ ReLU ก็จะเขียนสรุปในนี้ด้วย)
sigmoid
ฟังก์ชันกระตุ้นที่นิยมใช้กันมาช้านานตั้งแต่ยุคแรก
..(19.1)
นิยามคลาสได้ดังนี้ (คลาส Chan ให้นำเข้าจาก unagi.py เช่นเคย)
import numpy as np
import matplotlib.pyplot as plt
from unagi import chan
class Sigmoid(Chan):
def pai(self,a):
self.h = 1/(1+np.exp(-a))
return self.h
def yon(self,g):
return g*(1.-self.h)*self.hขอสร้างฟังก์ชันขึ้นมาเพื่อสำหรับใช้วาดทั้งฟังก์ชันนี้และฟังก์ชันต่อไปด้วย และทำการวาดขึ้นมา
def plot(f):
a = np.linspace(-5,5,201)
h = f.pai(a)
plt.axes(aspect=1,xticks=range(-5,6),yticks=range(-5,6))
plt.plot(a,h,'#eeaaaa',lw=3)
plt.grid(ls=':')
plt.show()
plot(Sigmoid())
ReLU
ย่อมาจาก rectified linear unit
ถูกนำมาใช้ในโครงข่ายประสาทเทียมตั้งแต่ปี 2011 ด้วยโครงสร้างที่เรียบง่ายแต่กลับใช้ได้ผลดีจึงกลายเป็นฟังก์ชันกระตุ้นที่เป็นที่นิยมใช้ที่สุด
..(19.2)
plot(Relu())
class Relu(Chan):
def pai(self,x):
self.krong = (x>0)
return np.where(self.krong,x,0)
def yon(self,g):
return np.where(self.krong,g,0)
plot(Relu())
LReLU
ย่อมาจาก leaky rectified linear unit นิยามโดย
..(19.3)
คล้ายกับ ReLU แต่ว่าช่วงที่ต่ำกว่า 0 จะมีค่า โดยขึ้นกับค่า a ซึ่งเป็นค่าที่จะกำหนดเท่าไหร่ก็ได้ (ถ้า a=0 ก็จะกลายเป็น ReLU ธรรมดา)
class Lrelu(Chan):
def __init__(self,a=0.01):
self.a = a
def pai(self,x):
self.krong = (x>0)
return x*np.where(self.krong,1,self.a)
def yon(self,g):
return g*np.where(self.krong,1,self.a)
plot(Lrelu(0.1))
PReLU
ย่อมาจาก parametric rectified linear unit นิยามโดย
..(19.4)
คล้ายกับ LReLU เพียงแต่ a ในที่นี้เป็นพารามิเตอร์ซึ่งมีจำนวนเท่ากับจำนวนตัวแปรในชั้นนั้น และต้องปรับค่าให้เหมาะสมไปในขณะเรียนรู้
class Prelu(Chan):
def __init__(self,m,a=0.25):
self.param = [Param(np.ones(m)*a)]
def pai(self,x):
self.krong = (x>0)
self.x = x
return x*np.where(self.krong,1,self.param[0].kha)
def yon(self,g):
self.param[0].g += (self.x*(self.krong==0)).sum(0)
return g*np.where(self.krong,1,self.param[0].kha)
plot(Prelu(1,0.25))
จะเห็นว่ามีพารามิเตอร์ที่ต้องเรียนรู้และปรับค่า ซึ่งต่างจากฟังก์ชันกระตุ้นทั่วๆไปชนิดอื่น
ELU
ย่อมาจาก exponential rectified linear unit
คล้าย ReLU แต่ครึ่งลบจะนิยามโดยเอกซ์โพเนนเชียล
..(19.5)
class Elu(Chan):
def __init__(self,a=1):
self.a = a
def pai(self,x):
self.krong = (x>0)
self.h = np.where(self.krong,x,self.a*(np.exp(x)-1))
return self.h
def yon(self,g):
return g*np.where(self.krong,1,(self.h+self.a))
plot(Elu(1))
SELU
ย่อมาจาก scaled exponential rectified linear unit
คล้ายกับ ELU แต่มีการคูณ λ เข้าไปอีก
..(19.6)
โดยที่ λ และ a ในที่นี้เป็นค่าที่ถูกกำหนดตายตัว
λ = 1.0507009873554804934193349852946
a = 1.6732632423543772848170429916717
ค่านี้เป็นค่าปรับสเกลที่ได้จากการวิจัยแล้วพบว่าได้ผลออกมาลงตัวน่าพอใจ
class Selu(Chan):
a = 1.6732632423543772848170429916717
l = 1.0507009873554804934193349852946
def pai(self,x):
self.krong = (x>0)
self.h = self.l*np.where(self.krong,x,self.a*(np.exp(x)-1))
return self.h
def yon(self,g):
return g*self.l*np.where(self.krong,1,(self.h+self.a))
plot(Selu())
tanh
เป็นฟังก์ชันไฮเพอร์โบลิก ซึ่งมีหน้าตาคล้ายซิกมอยด์ เพียงแต่มีค่าอยู่ในช่วง -1 ถึง 1
..(19.7)
class Tanh(Chan):
def pai(self,x):
self.h = np.tanh(x)
return self.h
def yon(self,g):
return g*(1-self.h**2)
plot(Tanh())
softsign
มีค่าอยู่ในช่วง -1 ถึง 1 คล้าย tanh
..(19.8)
class Softsign(Chan):
def pai(self,x):
self.abs_x_1 = np.abs(x)+1
return x/self.abs_x_1
def yon(self,g):
return g/self.abs_x_1**2
plot(Softsign())
softplus
ที่ค่าไกลจาก 0 จะคล้าย ReLU แต่ที่ค่าใกล้ 0 จะเป็นเส้นโค้งแทนที่จะหักมุม
..(19.9)
class Softplus(Chan):
def pai(self,x):
self.exp_x = np.exp(x)
return np.log(1+self.exp_x)
def yon(self,g):
return g*self.exp_x/(1+self.exp_x)
plot(Softplus())
สุดท้ายลองวาดภาพรวมทั้งหมดเทียบกันดู
chue = [u'ReLU',u'LReLU(0.1)',u'PReLU(0.25)',u'ELU(1)',u'SELU',u'softplus',u'sigmoid',u'tanh',u'softsign']
plt.figure(figsize=[7,5])
for i,f in enumerate([Relu(),Lrelu(0.1),Prelu(1,0.25),Elu(1),Selu(),Softplus(),Sigmoid(),Tanh(),Softsign()]):
a = np.linspace(-4,4,201)
h = f.pai(a)
plt.subplot(331+i,aspect=1,xlim=[-4,4],xticks=range(-5,6),yticks=range(-5,6))
plt.title(chue[i])
plt.plot(a,h,color=np.random.random(3),lw=2)
plt.grid(ls='--')
plt.tight_layout()
plt.show()
นอกจากนี้ก็ยังมีฟังก์ชันอื่นๆที่ไม่ได้แนะนำ และยังอาจมีฟังก์ชันใหม่ๆถูกคิดขึ้นมาและเป็นที่นิยมขึ้นมาอีกในอนาคต
>> อ่านต่อ บทที่ ๒๐
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy