[python] การเรกูลาไรซ์เพื่อป้องกันการเรียนรู้เกิน
เขียนเมื่อ 2017/09/28 07:59
แก้ไขล่าสุด 2021/09/28 16:42
ก่อนหน้านี้ได้พูดถึงการป้องกันการเรียนรู้เกินด้วยการแบ่งข้อมูลส่วนหนึ่งมาใช้ตรวจสอบ https://phyblas.hinaboshi.com/20170924
คราวนี้จะพูดถึงอีกวิธีหนึ่งในการแก้ปัญหาการเรียนรู้เกิน ก็คือการเรกูลาไรซ์ (正规化, regularize)
คำนี้หากแปลเป็นไทยตรงๆก็คือการทำให้เป็นแบบแผนหรือเป็นปกติทั่วไป แต่ความหมายในที่นี้ก็คือ การทำให้ค่าพารามิเตอร์น้ำหนักบางตัวภายในโมเดลไม่สูงมากจนเกินไป
ที่ค่าน้ำหนักบางตัวมากเกินแล้วจะไม่ดี นั่นเพราะจะทำให้ผลลัพธ์ขึ้นกับตัวแปรที่มีน้ำหนักเยอะนั่นมากเกินไป ดังนั้นถ้าหากค่าตัวนั้นอยู่ดีๆเปลี่ยนไปมาก ผลลัพธ์การทายก็อาจจะพลิกกลับทันทีเลย
ยกตัวอย่างเช่นว่า ในสังคมกลุ่มที่เราอยู่นั้น พบว่าคนที่เขียนไพธอนส่วนใหญ่นิสัยดี ดังนั้นเลยทำให้เกิดอคติขึ้นมาว่า ถ้าเจอคนเขียนไพธอนแสดงว่าคนนั้นน่าจะนิสัยดี
แต่ว่านั่นอาจจะเป็นแค่เพราะว่าในสังคมที่เราอยู่บังเอิญเจอคนเขียนไพธอนที่นิสัยดีเยอะเท่านั้นเอง ถ้าออกมาสู่สังคมอื่นอาจจะเจอคนเขียนไพธอนที่นิสัยไม่ดีเยอะก็เป็นได้
นี่เป็นลักษณะของความโน้มเอียงที่เกิดจากข้อมูลกลุ่มใดกลุ่มหนึ่งที่มีอยู่จำกัด ถ้าหลงไปตัดสินปรับเปลี่ยนระบบความคิดการติดสินของตัวเองจากข้อมูลที่มีอยู่แค่นั้นก็อาจจะทำให้เราประเมินข้อมูลกลุ่มใหม่ได้ผิด
ดังนั้นการเรกูลาไรซ์ในที่นี้จึงเปรียบเหมือนเป็นการลดการสร้างอคติ ให้เราไม่รีบด่วนตัดสินอะไรอย่างสุดขั้วจากแค่ข้อมูลที่มีอยู่
คนเรามักจำเป็นต้องตัดสินอะไรจากประสบการณ์ตรงที่ตัวเองเคยเจอและข้อมูลที่มีในมือ นั่นไม่ใช่เรื่องผิดอะไร เพราะข้อมูลที่มีมักถูกจำกัดด้วยฐานะและเวลา
แต่ควรเผื่อใจไว้ว่าบางทีอาจเจอสิ่งใหม่ที่ไม่เป็นไปตามนั้นก็เป็นได้ ยิ่งถ้าเจอสังคมใหม่ที่แปลกไปจากเดิมมากๆ
ยังไงการตัดสินอะไรอย่างสุดขั้วจากข้อมูลที่มีอยู่แค่เพียงจำกัดไม่น่าจะใช่เรื่องดี
ที่จริงจะไม่ใช่ปัญหาอะไรมากถ้าหากตัวอย่างที่เราให้โปรแกรมใช้ในการเรียนรู้นั้นมีความครอบคลุมแทบทุกรูปแบบที่เป็นไปได้
แต่ในสถานการณ์ทั่วไปเป็นไปได้ยากที่จะเตรียมตัวอย่างให้ครอบคลุม ดังนั้นจึงต้องมีการป้องกันการเรียนรู้เกิน
ยิ่งข้อมูลที่นำมาใช้ฝึกฝนนั้นมีความหลากหลายไม่พอ ไม่ครอบคลุม การเรียนรู้เกินจะยิ่งเกิดขึ้นได้ง่าย
ขอยกตัวอย่างที่เราสามารถลองเขียนโปรแกรมดูผลได้เห็นชัดเจน ก็คือการแยกแยะตัวเลขจากข้อมูล MNIST ซึ่งได้พูดถึงไปแล้วตั้งแต่หน้า https://phyblas.hinaboshi.com/20170922
ต่อไปจะลองเขียนโค้ดแสดงผลการเรียนรู้ข้อมูล MNIST โดยใช้คลาส ThotthoiLogistic ซึ่งเขียนขึ้นและใช้ไปใน https://phyblas.hinaboshi.com/20170924
ส่วนของโค้ดที่นิยามตัวคลาสสามารถคัดลอกมาจากหน้านี้ได้ https://github.com/phyblas/rianrupython/blob/master/kanrianrukhongkhrueang/thotthoi_mnist_2.py
ลองดึงข้อมูล MNIST ทั้งหมดซึ่งมีถึง 70000 ภาพมาแล้วให้โมเดลของเราอันนี้ทำการเรียนรู้ จากนั้นลองวาดภาพที่แสดงถึงน้ำหนัก
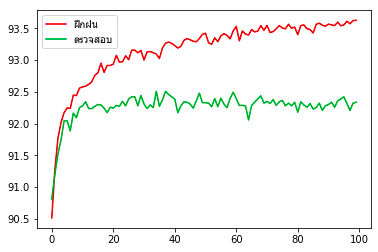
ผลที่ได้จะเห็นแบบนี้ ความแม่นยำในการทายข้อมูลฝึกกับข้อมูลตรวจสอบนั้นต่างกันนิดเดียว แสดงว่าการเรียนรู้เกินเกิดขึ้นน้อย นั่นเพราะจำนวนข้อมูลรวมมีถึง 70000 (ใช้ฝึกฝนจริง 80% = 56000) นั้นเป็นจำนวนที่มากพอสมควร
ส่วนภาพแสดงการกระจายของน้ำหนักนั้น ในที่นี้สีแดงคือบริเวณที่น้ำหนักเป็นบวกมาก คือถ้าหากโดนขีดแล้วจะมีโอกาสเป็นเลขนั้นมาก
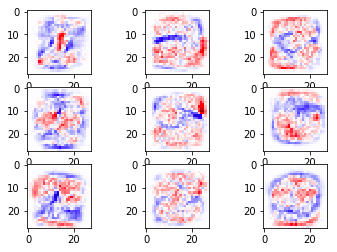
ส่วนสีน้ำเงินคือบริเวณที่น้ำหนักติดลบ ถ้าโดนขีดจะไม่น่าเป็น
และสีขาวคือบริเวณที่น้ำหนักเป็น 0 คือแทบไม่สำคัญ แทบไม่ถูกนำมาพิจารณา
จากนั้นลองวาดใหม่โดยคราวนี้สุ่มดึงข้อมูลมาใช้แค่ 1% ก็คือ 700 ภาพ
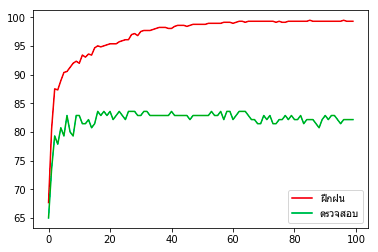
นำมาแยกเป็นข้อมูลฝึกฝนและทดสอบ แล้วให้เรียนรู้แบบเดิม แล้ววาดภาพแบบเดิมใหม่ ผลที่ได้ก็คือความแม่นยำในการทายข้อมูลพุ่งขึ้นสูงเกือบ 100% แต่พอทำนายชุดข้อมูลตรวจสอบกลับได้ถูก 83% เท่านั้น
ส่วนภาพแสดงน้ำหนักก็เห็นเป็นเค้าโครงตัวเลขชัดเจนขึ้นมาก
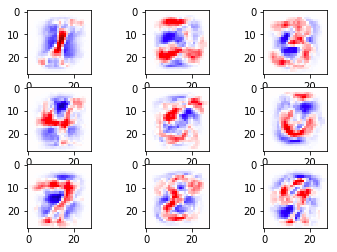
สาเหตุที่เป็นแบบนี้เพราะว่าพอตัวอย่างมีน้อยลง ผลที่ได้ก็เกิดจากการสรุปจากในกลุ่มข้อมูลที่น้อยลง จึงมีความเป็นทั่วไปลดลง ถ้าบังเอิญตัวอย่างที่ยกมานั้นมีการขีดบริเวณนั้นเยอะ ตรงนั้นก็จะเป็นสีแดงได้ง่าย
ซึ่งแบบนี้จะทายผิดได้ง่าย เมื่อเจอตัวอย่างใหม่ที่เส้นไม่ได้ลากไปโดนตรงนั้น
นี่จึงเป็นสิ่งที่แสดงถึงการเรียนรู้เกินอย่างเห็นได้ชัด
ดังนั้นคราวนี้จะมาเขียนคลาสขึ้นใหม่ โดยเพิ่มการเรกูลาไรซ์เข้าไป
วิธีการเรกูลาไรซ์เพื่อไม่ให้ค่าน้ำหนักมากเกินไปก็คือการเพิ่มค่าเสียหายขึ้นตามค่าน้ำหนักขณะนั้น
ฟังก์ชันที่นิยมใช้บวกเพิ่มเข้าไปนั้นมี ๒ แบบคือ l1 กับ l2
l2 คือการคิดค่าเสียหายเพิ่มตามค่าน้ำหนักยกกำลังสอง กล่าวคือ
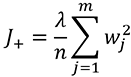
ในที่นี้ λ คือขนาดของการเรกูลาไรซ์ ยิ่งมากก็จะยิ่งถ่วงให้ค่ำน้ำหนักเพิ่มสูงได้ยาก เป็นพารามิเตอร์หนึ่งที่สำคัญ ต้องพิจารณาเลือกค่าให้เหมาะสม
ส่วน l1 จะคิดค่าเสียหายเพิ่มตามค่าสัมบูรณ์ของน้ำหนัก
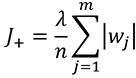
ค่าเสียหายส่วนนี้จะไปบวกเพิ่มจากค่าเสียหายเดิมซึ่งมาจากเอนโทรปีไขว้ หรือค่าเฉลี่ยผลรวมความคลาดเคลื่อนกำลังสอง
ส่วนค่าน้ำหนักที่ต้องปรับแก้ในแต่ละรอบนั้นก็ขึ้นกับอนุพันธ์ของค่านี้ กรณี l2 คำนวณค่าอนุพันธ์ได้เป็น
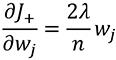
ส่วน l1 นั้นเป็นฟังก์ชันไม่ต่อเนื่อง ต้องแบ่งเป็น ๓ ส่วนคือถ้ามากกว่า 0 จะเป็น λ/n ถ้าน้อยกว่า 0 จะเป็น -λ/n ถ้าเป็น 0 อยู่แล้วก็เป็น 0
หากเขียนเป็นโค้ดก็จะได้แบบนี้
ในที่นี้ l แทน λ ส่วน n คือจำนวนข้อมูลฝึก ส่วน J และ w เป็นอาเรย์
J คือค่าเสียหายที่มาจากเอนโทรปีหรือค่าเฉลี่ยผลรวมความคลาดเคลื่อนกำลังสองอยู่ก่อนแล่้ว นำมาบวกเพิ่มค่าเสียหายจาก
ของ l1 นั้น np.where(self.w>0,1,-1) หมายความว่าถ้า w มากกว่า 0 จะเป็น 1 แต่ถ้า w น้อยกว่า 0 จะเป็น -1
ส่วน (self.w!=0) นั้นจะทำให้เป็น 0 เมื่อ w เป็น 0 นอกนั้นจะเป็น 1
เพื่อให้เข้าใจง่ายมาวาดภาพแสดงค่าเสียหายกันให้เห็นภาพชัดว่าพอเพิ่มเรกูลาไรซ์ลงไปในค่าเสียหายแล้วจะเกิดอะไรขึ้น
สมมุติว่าฟังก์ชันค่าเสียหายเดิมของเราเป็นดังระนาบสีน้ำเงินแบบนี้ เป็นแอ่งที่มีจุดต่ำสุดอยู่ที่จุดสีน้ำเงิน คือจุด (1,2)
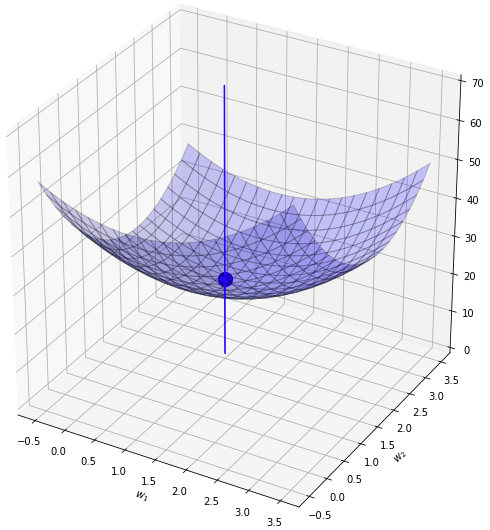
จากนั้นเพิ่มเรกูลาไรซ์แบบ l2 เข้ามาก็เหมือนเป็นการบวกเพิ่มฟังก์ชันที่มีการบุ๋มตรงจุด (0,0) ดังรูปนี้
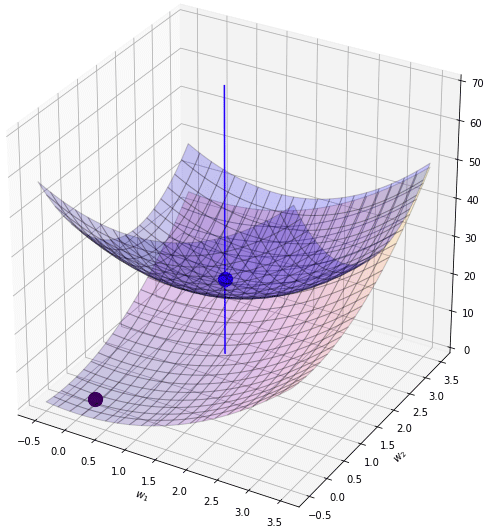
พอนำค่าทั้ง ๒ มาบวกกันก็จะได้กลายเป็นระนาบเขียว ซึ่งมีจุดต่ำสุดใหม่ที่ใกล้ใจกลางมากขึ้น คืออยู่ที่ (0.6,1.43)
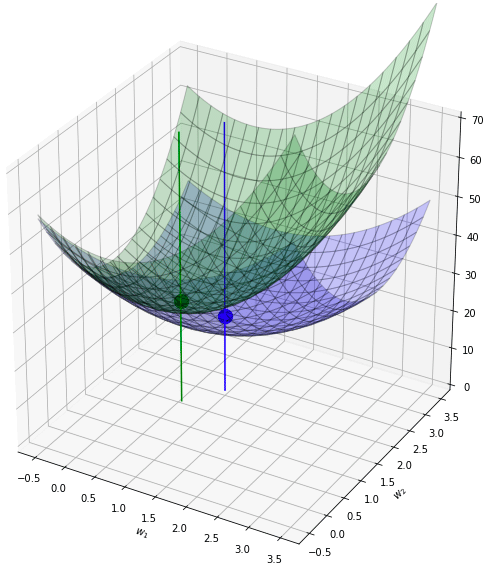
ทีนี้ถ้าหากเปลี่ยนใหม่มาเป็น l1 จะเป็นยังไง? l1 นั้นคล้ายๆกับ l2 คือทำให้เกิดการยุบตรงกลาง แต่จะเห็นว่าร่องเป็นเหลี่ยม เป็นหุบเขาแหลมชัน
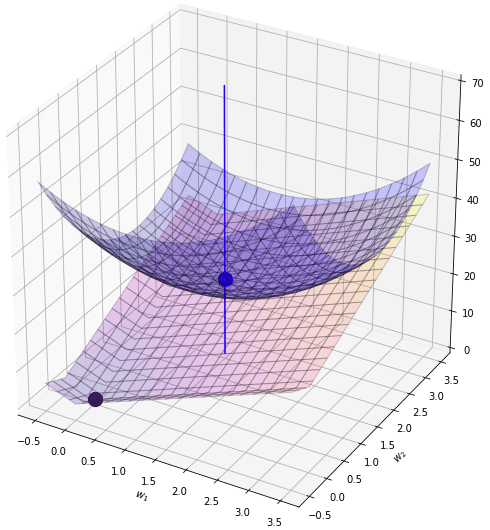
ตรงนี้ที่จุดที่ w1 หรือ w2 เป็น 0 เป็นจุดหักมุมอย่างชัดเจน ดังนั้นพอนำมาบวกกันจึงทำให้จุดต่ำสุดไปเกิดที่ 0 ได้อย่างง่ายได้
ลองรวมกันดู ผลก็คือจุดต่ำสุดไปอยู่ที่ (0.0,1.4) ดูแล้วก็เหมือนกับว่าเป็นการตกร่อง
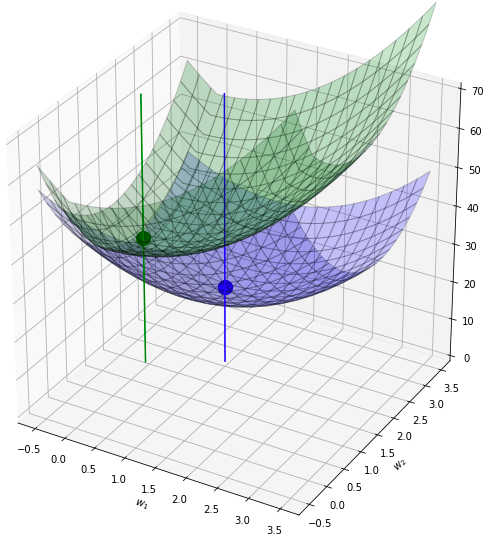
ดังนั้นลักษณะเด่นของ l1 ก็คือ ทำให้ค่าน้ำหนักบางตัวที่น้อยอยู่แล้วกลายเป็น 0 ได้อย่างง่ายดาย
นี่เป็นตัวอย่างของระบบที่มีค่าน้ำหนักแค่ 2 ตัว ส่วนข้อมูล MNIST มี 784 ตัวอาจมองภาพได้ยากสักหน่อยแต่ก็หลักการเดียวกัน
ภาพข้างต้นนี้วาดโดยโค้ดตามนี้
ต่อมา ลองนิยามคลาสของโมเดลใหม่ที่ได้เพิ่มการเรกูลาไรซ์นี้ขึ้นมา จากนั้นก็นำมาใช้เพื่อเรียนรู้ข้อมูลชุดเดิม ลองให้ λ เป็น 80 แล้วใช้การเรกูลาไรซ์แบบ l2
λ ในที่นี้แทนด้วยตัวแปร l ส่วนรูปแบบของการเรกูลาไรซ์แทนด้วยตัวแปร reg โดยจะมีค่าได้แค่ ๒ แบบคือ l1 และ l2 ทั้งสองอย่างนี้ให้กำหนดตั้งแต่ตอนสร้างคลาสขึ้นเลย แต่ถ้าไม่ใส่ก็จะถือว่าเป็น 0 คือไม่มีการเรกูลาไรซ์
ผลที่ได้ลองเอามาเปรียบเทียบกับผลก่อนหน้าซึ่งไม่มีการเรกูลาไรซ์ก็จะพบว่าความแม่นของการทำนายชุดข้อมูลตรวจสอบไม่ได้ต่างจากเดิมมาก แต่ของชุดข้อมูลฝึกฝนลดลงอย่างมาก แสดงว่าการเรียนรู้เกินลดลงไปมาก
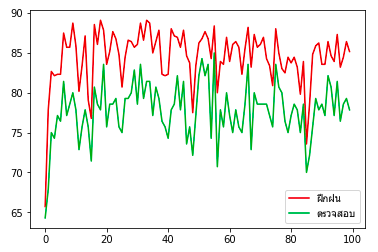
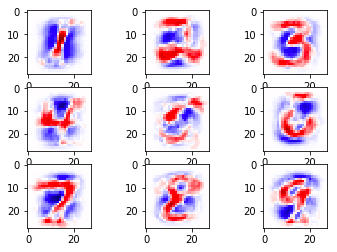
เพียงแต่ว่าค่า λ (ในที่นี้คือ l) นั้นจำเป็นต้องปรับให้เหมาะสม หากมากไปก็กลับจะทำให้การเรียนรู้ไม่คืบหน้า เพราะน้ำหนักจะเข้าใกล้ 0 กันมากไป กลับกลายเป็นผลเสีย
เช่นลองให้ l = 800 คราวนี้จะพบว่าผลการทายกลายเป็นไม่แม่นไปเลย
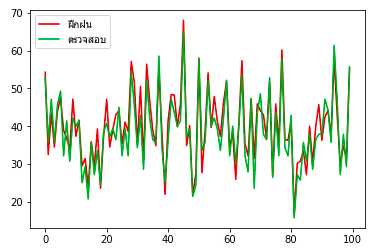
ต่อมาลองดูแบบ l1 บ้าง ลองแก้ reg เป็น l1 แล้วก็วาดภาพแสดงการกระจายของค่าน้ำหนัก
จะได้ภาพแบบนี้ ซึ่งเห็นได้ว่าบริเวณสีขาวมีมากขึ้น คือถูกลดค่ากลายเป็น 0 เห็นได้ชัดเจน
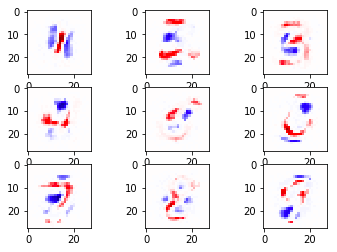
นี่แสดงให้เห็นถึงลักษณะเด่นของ l1 ที่ว่าจะทำให้เกิดค่าน้ำหนักเป็น 0 มาก
อ้างอิง
คราวนี้จะพูดถึงอีกวิธีหนึ่งในการแก้ปัญหาการเรียนรู้เกิน ก็คือการเรกูลาไรซ์ (正规化, regularize)
คำนี้หากแปลเป็นไทยตรงๆก็คือการทำให้เป็นแบบแผนหรือเป็นปกติทั่วไป แต่ความหมายในที่นี้ก็คือ การทำให้ค่าพารามิเตอร์น้ำหนักบางตัวภายในโมเดลไม่สูงมากจนเกินไป
ที่ค่าน้ำหนักบางตัวมากเกินแล้วจะไม่ดี นั่นเพราะจะทำให้ผลลัพธ์ขึ้นกับตัวแปรที่มีน้ำหนักเยอะนั่นมากเกินไป ดังนั้นถ้าหากค่าตัวนั้นอยู่ดีๆเปลี่ยนไปมาก ผลลัพธ์การทายก็อาจจะพลิกกลับทันทีเลย
ยกตัวอย่างเช่นว่า ในสังคมกลุ่มที่เราอยู่นั้น พบว่าคนที่เขียนไพธอนส่วนใหญ่นิสัยดี ดังนั้นเลยทำให้เกิดอคติขึ้นมาว่า ถ้าเจอคนเขียนไพธอนแสดงว่าคนนั้นน่าจะนิสัยดี
แต่ว่านั่นอาจจะเป็นแค่เพราะว่าในสังคมที่เราอยู่บังเอิญเจอคนเขียนไพธอนที่นิสัยดีเยอะเท่านั้นเอง ถ้าออกมาสู่สังคมอื่นอาจจะเจอคนเขียนไพธอนที่นิสัยไม่ดีเยอะก็เป็นได้
นี่เป็นลักษณะของความโน้มเอียงที่เกิดจากข้อมูลกลุ่มใดกลุ่มหนึ่งที่มีอยู่จำกัด ถ้าหลงไปตัดสินปรับเปลี่ยนระบบความคิดการติดสินของตัวเองจากข้อมูลที่มีอยู่แค่นั้นก็อาจจะทำให้เราประเมินข้อมูลกลุ่มใหม่ได้ผิด
ดังนั้นการเรกูลาไรซ์ในที่นี้จึงเปรียบเหมือนเป็นการลดการสร้างอคติ ให้เราไม่รีบด่วนตัดสินอะไรอย่างสุดขั้วจากแค่ข้อมูลที่มีอยู่
คนเรามักจำเป็นต้องตัดสินอะไรจากประสบการณ์ตรงที่ตัวเองเคยเจอและข้อมูลที่มีในมือ นั่นไม่ใช่เรื่องผิดอะไร เพราะข้อมูลที่มีมักถูกจำกัดด้วยฐานะและเวลา
แต่ควรเผื่อใจไว้ว่าบางทีอาจเจอสิ่งใหม่ที่ไม่เป็นไปตามนั้นก็เป็นได้ ยิ่งถ้าเจอสังคมใหม่ที่แปลกไปจากเดิมมากๆ
ยังไงการตัดสินอะไรอย่างสุดขั้วจากข้อมูลที่มีอยู่แค่เพียงจำกัดไม่น่าจะใช่เรื่องดี
ที่จริงจะไม่ใช่ปัญหาอะไรมากถ้าหากตัวอย่างที่เราให้โปรแกรมใช้ในการเรียนรู้นั้นมีความครอบคลุมแทบทุกรูปแบบที่เป็นไปได้
แต่ในสถานการณ์ทั่วไปเป็นไปได้ยากที่จะเตรียมตัวอย่างให้ครอบคลุม ดังนั้นจึงต้องมีการป้องกันการเรียนรู้เกิน
ยิ่งข้อมูลที่นำมาใช้ฝึกฝนนั้นมีความหลากหลายไม่พอ ไม่ครอบคลุม การเรียนรู้เกินจะยิ่งเกิดขึ้นได้ง่าย
ขอยกตัวอย่างที่เราสามารถลองเขียนโปรแกรมดูผลได้เห็นชัดเจน ก็คือการแยกแยะตัวเลขจากข้อมูล MNIST ซึ่งได้พูดถึงไปแล้วตั้งแต่หน้า https://phyblas.hinaboshi.com/20170922
ต่อไปจะลองเขียนโค้ดแสดงผลการเรียนรู้ข้อมูล MNIST โดยใช้คลาส ThotthoiLogistic ซึ่งเขียนขึ้นและใช้ไปใน https://phyblas.hinaboshi.com/20170924
ส่วนของโค้ดที่นิยามตัวคลาสสามารถคัดลอกมาจากหน้านี้ได้ https://github.com/phyblas/rianrupython/blob/master/kanrianrukhongkhrueang/thotthoi_mnist_2.py
ลองดึงข้อมูล MNIST ทั้งหมดซึ่งมีถึง 70000 ภาพมาแล้วให้โมเดลของเราอันนี้ทำการเรียนรู้ จากนั้นลองวาดภาพที่แสดงถึงน้ำหนัก
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
np.random.seed(0)
mnist = datasets.fetch_mldata('MNIST original')
X,z = mnist.data,mnist.target
X = X/255.
X_fuek,X_truat,z_fuek,z_truat = train_test_split(X,z,test_size=0.2)
eta = 0.24
n_thamsam = 50
n_batch = 100
tl = ThotthoiLogistic(eta)
tl.rianru(X_fuek,z_fuek,n_thamsam,n_batch,X_truat,z_truat)
plt.plot(tl.maen_fuek,'#dd0000')
plt.plot(tl.maen_truat,'#00aa33')
plt.legend([u'ฝึกฝน',u'ตรวจสอบ'],prop={'family':'Tahoma'})
plt.figure()
w = tl.w[1:]
si = plt.get_cmap('seismic')(w/np.abs(w).max()/2+0.5)
for i in range(1,10):
plt.subplot(330+i)
plt.imshow(si[:,i].reshape(28,28,4))
plt.show()
print('%.3f%% / %.3f%%'%(max(tl.maen_fuek),max(tl.maen_truat)))ผลที่ได้จะเห็นแบบนี้ ความแม่นยำในการทายข้อมูลฝึกกับข้อมูลตรวจสอบนั้นต่างกันนิดเดียว แสดงว่าการเรียนรู้เกินเกิดขึ้นน้อย นั่นเพราะจำนวนข้อมูลรวมมีถึง 70000 (ใช้ฝึกฝนจริง 80% = 56000) นั้นเป็นจำนวนที่มากพอสมควร

ส่วนภาพแสดงการกระจายของน้ำหนักนั้น ในที่นี้สีแดงคือบริเวณที่น้ำหนักเป็นบวกมาก คือถ้าหากโดนขีดแล้วจะมีโอกาสเป็นเลขนั้นมาก

ส่วนสีน้ำเงินคือบริเวณที่น้ำหนักติดลบ ถ้าโดนขีดจะไม่น่าเป็น
และสีขาวคือบริเวณที่น้ำหนักเป็น 0 คือแทบไม่สำคัญ แทบไม่ถูกนำมาพิจารณา
จากนั้นลองวาดใหม่โดยคราวนี้สุ่มดึงข้อมูลมาใช้แค่ 1% ก็คือ 700 ภาพ
sumriang = np.random.permutation(len(mnist.target))
X = mnist.data[sumriang[:700]]
z = mnist.target[sumriang[:700]]นำมาแยกเป็นข้อมูลฝึกฝนและทดสอบ แล้วให้เรียนรู้แบบเดิม แล้ววาดภาพแบบเดิมใหม่ ผลที่ได้ก็คือความแม่นยำในการทายข้อมูลพุ่งขึ้นสูงเกือบ 100% แต่พอทำนายชุดข้อมูลตรวจสอบกลับได้ถูก 83% เท่านั้น

ส่วนภาพแสดงน้ำหนักก็เห็นเป็นเค้าโครงตัวเลขชัดเจนขึ้นมาก

สาเหตุที่เป็นแบบนี้เพราะว่าพอตัวอย่างมีน้อยลง ผลที่ได้ก็เกิดจากการสรุปจากในกลุ่มข้อมูลที่น้อยลง จึงมีความเป็นทั่วไปลดลง ถ้าบังเอิญตัวอย่างที่ยกมานั้นมีการขีดบริเวณนั้นเยอะ ตรงนั้นก็จะเป็นสีแดงได้ง่าย
ซึ่งแบบนี้จะทายผิดได้ง่าย เมื่อเจอตัวอย่างใหม่ที่เส้นไม่ได้ลากไปโดนตรงนั้น
นี่จึงเป็นสิ่งที่แสดงถึงการเรียนรู้เกินอย่างเห็นได้ชัด
ดังนั้นคราวนี้จะมาเขียนคลาสขึ้นใหม่ โดยเพิ่มการเรกูลาไรซ์เข้าไป
วิธีการเรกูลาไรซ์เพื่อไม่ให้ค่าน้ำหนักมากเกินไปก็คือการเพิ่มค่าเสียหายขึ้นตามค่าน้ำหนักขณะนั้น
ฟังก์ชันที่นิยมใช้บวกเพิ่มเข้าไปนั้นมี ๒ แบบคือ l1 กับ l2
l2 คือการคิดค่าเสียหายเพิ่มตามค่าน้ำหนักยกกำลังสอง กล่าวคือ
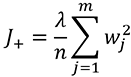
ในที่นี้ λ คือขนาดของการเรกูลาไรซ์ ยิ่งมากก็จะยิ่งถ่วงให้ค่ำน้ำหนักเพิ่มสูงได้ยาก เป็นพารามิเตอร์หนึ่งที่สำคัญ ต้องพิจารณาเลือกค่าให้เหมาะสม
ส่วน l1 จะคิดค่าเสียหายเพิ่มตามค่าสัมบูรณ์ของน้ำหนัก
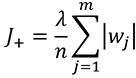
ค่าเสียหายส่วนนี้จะไปบวกเพิ่มจากค่าเสียหายเดิมซึ่งมาจากเอนโทรปีไขว้ หรือค่าเฉลี่ยผลรวมความคลาดเคลื่อนกำลังสอง
ส่วนค่าน้ำหนักที่ต้องปรับแก้ในแต่ละรอบนั้นก็ขึ้นกับอนุพันธ์ของค่านี้ กรณี l2 คำนวณค่าอนุพันธ์ได้เป็น
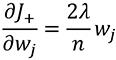
ส่วน l1 นั้นเป็นฟังก์ชันไม่ต่อเนื่อง ต้องแบ่งเป็น ๓ ส่วนคือถ้ามากกว่า 0 จะเป็น λ/n ถ้าน้อยกว่า 0 จะเป็น -λ/n ถ้าเป็น 0 อยู่แล้วก็เป็น 0
หากเขียนเป็นโค้ดก็จะได้แบบนี้
J += 2*w*l/n #l2
J += (w!=0)*np.where(w>0,1,-1)*l/n #l1ในที่นี้ l แทน λ ส่วน n คือจำนวนข้อมูลฝึก ส่วน J และ w เป็นอาเรย์
J คือค่าเสียหายที่มาจากเอนโทรปีหรือค่าเฉลี่ยผลรวมความคลาดเคลื่อนกำลังสองอยู่ก่อนแล่้ว นำมาบวกเพิ่มค่าเสียหายจาก
ของ l1 นั้น np.where(self.w>0,1,-1) หมายความว่าถ้า w มากกว่า 0 จะเป็น 1 แต่ถ้า w น้อยกว่า 0 จะเป็น -1
ส่วน (self.w!=0) นั้นจะทำให้เป็น 0 เมื่อ w เป็น 0 นอกนั้นจะเป็น 1
เพื่อให้เข้าใจง่ายมาวาดภาพแสดงค่าเสียหายกันให้เห็นภาพชัดว่าพอเพิ่มเรกูลาไรซ์ลงไปในค่าเสียหายแล้วจะเกิดอะไรขึ้น
สมมุติว่าฟังก์ชันค่าเสียหายเดิมของเราเป็นดังระนาบสีน้ำเงินแบบนี้ เป็นแอ่งที่มีจุดต่ำสุดอยู่ที่จุดสีน้ำเงิน คือจุด (1,2)

จากนั้นเพิ่มเรกูลาไรซ์แบบ l2 เข้ามาก็เหมือนเป็นการบวกเพิ่มฟังก์ชันที่มีการบุ๋มตรงจุด (0,0) ดังรูปนี้

พอนำค่าทั้ง ๒ มาบวกกันก็จะได้กลายเป็นระนาบเขียว ซึ่งมีจุดต่ำสุดใหม่ที่ใกล้ใจกลางมากขึ้น คืออยู่ที่ (0.6,1.43)

ทีนี้ถ้าหากเปลี่ยนใหม่มาเป็น l1 จะเป็นยังไง? l1 นั้นคล้ายๆกับ l2 คือทำให้เกิดการยุบตรงกลาง แต่จะเห็นว่าร่องเป็นเหลี่ยม เป็นหุบเขาแหลมชัน

ตรงนี้ที่จุดที่ w1 หรือ w2 เป็น 0 เป็นจุดหักมุมอย่างชัดเจน ดังนั้นพอนำมาบวกกันจึงทำให้จุดต่ำสุดไปเกิดที่ 0 ได้อย่างง่ายได้
ลองรวมกันดู ผลก็คือจุดต่ำสุดไปอยู่ที่ (0.0,1.4) ดูแล้วก็เหมือนกับว่าเป็นการตกร่อง

ดังนั้นลักษณะเด่นของ l1 ก็คือ ทำให้ค่าน้ำหนักบางตัวที่น้อยอยู่แล้วกลายเป็น 0 ได้อย่างง่ายดาย
นี่เป็นตัวอย่างของระบบที่มีค่าน้ำหนักแค่ 2 ตัว ส่วนข้อมูล MNIST มี 784 ตัวอาจมองภาพได้ยากสักหน่อยแต่ก็หลักการเดียวกัน
ภาพข้างต้นนี้วาดโดยโค้ดตามนี้
from mpl_toolkits.mplot3d import Axes3D
x,y = np.meshgrid(np.linspace(-0.5,3.5,401),np.linspace(-0.5,3.5,401))
z = 20+(x-1)**2*3+(y-2)**2*5
l1 = (np.abs(x)+np.abs(y))*6
l2 = (x**2+y**2)*2
z2 = z+l1
# z2 = z+l2
zargmin = z.argmin()
ct = (zargmin//401,zargmin%401)
z2argmin = z2.argmin()
ct2 = (z2argmin//401,z2argmin%401)
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d',xlabel='$w_1$',ylabel='$w_2$')
ax.set_zlim(0,z.max())
ax.plot_surface(x,y,z,rstride=20,cstride=20,alpha=0.2,color='b',edgecolor='k')
ax.scatter(x[ct],y[ct],z.min(),c='b',sizes=[200])
ax.plot([x[ct]]*2,[y[ct]]*2,[0,z.max()],c='b')
# ax.plot_surface(x,y,l2,rstride=20,cstride=20,alpha=0.2,cmap='plasma',edgecolor='k')
# ax.plot_surface(x,y,l1,rstride=20,cstride=20,alpha=0.2,cmap='plasma',edgecolor='k')
# ax.scatter(0,0,0,c='#770077',sizes=[200])
ax.plot_surface(x,y,z2,rstride=20,cstride=20,alpha=0.2,color='g',edgecolor='k')
ax.scatter(x[ct2],y[ct2],z2.min(),c='g',sizes=[200])
ax.plot([x[ct2]]*2,[y[ct2]]*2,[0,z.max()],c='g')
plt.show()ต่อมา ลองนิยามคลาสของโมเดลใหม่ที่ได้เพิ่มการเรกูลาไรซ์นี้ขึ้นมา จากนั้นก็นำมาใช้เพื่อเรียนรู้ข้อมูลชุดเดิม ลองให้ λ เป็น 80 แล้วใช้การเรกูลาไรซ์แบบ l2
λ ในที่นี้แทนด้วยตัวแปร l ส่วนรูปแบบของการเรกูลาไรซ์แทนด้วยตัวแปร reg โดยจะมีค่าได้แค่ ๒ แบบคือ l1 และ l2 ทั้งสองอย่างนี้ให้กำหนดตั้งแต่ตอนสร้างคลาสขึ้นเลย แต่ถ้าไม่ใส่ก็จะถือว่าเป็น 0 คือไม่มีการเรกูลาไรซ์
def softmax(x):
exp_x = np.exp(x.T-x.max(1))
return (exp_x/exp_x.sum(0)).T
class ThotthoiLogistic:
def __init__(self,eta,reg='l2',l=0):
self.eta = eta # อัตราการเรียนรู้
self.reg = reg # รูปแบบการเรกูลาไรซ์
self.l = l # ขนาดของเรกูลาไรซ์
def rianru(self,X,z,n_thamsam,n_batch=0,X_truat=0,z_truat=0,romaiphoem=0):
n = len(z)
if(type(X_truat)!=np.ndarray): # ถ้าไม่ได้ป้อนข้อมูลตรวจสอบมาด้วย ก็ให้ใช้ข้อมูลฝึกฝนเป็นข้อมูลตรวจสอบ
X_truat,z_truat = X,z
if(n_batch==0 or n<n_batch):
n_batch = n
self.kiklum = int(z.max()+1) # จำนวนผลลัพธ์
z_1h = z[:,None]==range(self.kiklum) # แปลงเป็น one-hot
self.w = np.zeros([X.shape[1]+1,self.kiklum]) # ค่าน้ำหนักตั้งต้นเป็น 0
self.dw = self.w.copy() # สร้างอาเรย์สำหรับพักค่าการเปลี่ยนแปลงน้ำหนักด้วย
self.khasiahai = [] # ลิสต์บันทึกค่าเสียหาย (เอนโทรปี+เรกูลาไรซ์)
self.maen_fuek = [] # ลิสต์บันทึกค่าความแม่นยำในการทำนายข้อมุลฝึก
self.maen_truat = [] # ลิสต์บันทึกค่าความแม่นยำในการทำนายข้อมุลตรวจสอบ
disut = 0 # ค่าความแม่นยำดีสุดที่ได้
maiphoem = 0 # นับว่าความแม่นยำไม่เพิ่มมาแล้วกี่ครั้ง
for j in range(n_thamsam):
lueak = np.random.permutation(n)
for i in range(0,n,n_batch):
Xn = X[lueak[i:i+n_batch]]
zn = z_1h[lueak[i:i+n_batch]]
phi = self.ha_softmax(Xn)
eee = (zn-phi)/len(zn)
self.dw[1:] = np.dot(eee.T,Xn).T
self.dw[0] = eee.sum(0)
# หาก l ไม่เป็น 0 ให้ปรับค่าน้ำหนักตามผลจากการเรกูลาไรซ์ด้วย
if(self.l>0):
if(self.reg=='l1'):
self.dw[1:] -= (self.w[1:]!=0)*np.where(self.w[1:]>0,1,-1)*self.l/n
else: # l2
self.dw[1:] -= 2*self.w[1:]*self.l/n
self.w += self.dw*self.eta
thukmai = self.thamnai(X)==z
maen_fuek = thukmai.mean()*100
thukmai = self.thamnai(X_truat)==z_truat
maen_truat = thukmai.mean()*100
khasiahai = self.ha_entropy(X,z_1h) # ค่าเสียหายจากเอนโทรปี
# หาก l ไม่เป็น 0 ให้บวกเรกูลาไรซ์เพิ่มเข้าไปในค่าเสียหายด้วย
if(self.l>0):
if(reg=='l1'):
khasiahai += self.l*np.abs(self.w[1:]).sum()
else: # l2
khasiahai += self.l*((self.w[1:])**2).sum()
if(maen_truat > disut):
# ถ้าจำนวนที่ถูกมากขึ้นกว่าเดิมก็บันทึกค่าจำนวนนั้น และน้ำหนักในตอนนั้นไว้
disut = maen_truat
maiphoem = 0
w = self.w.copy()
else:
maiphoem += 1 # ถ้าไม่ถูกมากขึ้นก็นับไว้ว่าไม่เพิ่มไปอีกครั้งแล้ว
self.maen_fuek.append(maen_fuek)
self.maen_truat.append(maen_truat)
self.khasiahai.append(khasiahai)
print(u'ครั้งที่ %d ถูก %.3f%% สูงสุด %.3f%% ไม่เพิ่มมาแล้ว %d ครั้ง'%(j+1,self.maen_truat[-1],disut,maiphoem))
if(romaiphoem!=0 and maiphoem>=romaiphoem):
break # ถ้าจำนวนที่ถูกไม่เพิ่มเลย 10 ครั้งก็เลิกทำ
self.w = w # ค่าน้ำหนักที่ได้ในท้ายสุด เอาตามค่าที่ทำให้ทายถูกมากที่สุด
def thamnai(self,X):
return (np.dot(X,self.w[1:])+self.w[0]).argmax(1)
def ha_softmax(self,X):
return softmax(np.dot(X,self.w[1:])+self.w[0])
def ha_entropy(self,X,z_1h):
return -(z_1h*np.log(self.ha_softmax(X)+1e-7)).mean()
eta = 0.2
n_thamsam = 100
n_batch = 100
reg = 'l2'
l = 800
tl = ThotthoiLogistic(eta,reg,l)
tl.rianru(X_fuek,z_fuek,n_thamsam,n_batch,X_truat,z_truat)
# โค้ดส่วนวาดกราฟขอละไว้ ไปดึงจากด้านบนมาใช้ผลที่ได้ลองเอามาเปรียบเทียบกับผลก่อนหน้าซึ่งไม่มีการเรกูลาไรซ์ก็จะพบว่าความแม่นของการทำนายชุดข้อมูลตรวจสอบไม่ได้ต่างจากเดิมมาก แต่ของชุดข้อมูลฝึกฝนลดลงอย่างมาก แสดงว่าการเรียนรู้เกินลดลงไปมาก


เพียงแต่ว่าค่า λ (ในที่นี้คือ l) นั้นจำเป็นต้องปรับให้เหมาะสม หากมากไปก็กลับจะทำให้การเรียนรู้ไม่คืบหน้า เพราะน้ำหนักจะเข้าใกล้ 0 กันมากไป กลับกลายเป็นผลเสีย
เช่นลองให้ l = 800 คราวนี้จะพบว่าผลการทายกลายเป็นไม่แม่นไปเลย

ต่อมาลองดูแบบ l1 บ้าง ลองแก้ reg เป็น l1 แล้วก็วาดภาพแสดงการกระจายของค่าน้ำหนัก
tl = ThotthoiLogistic(eta=0.24,reg='l1',l=5)
tl.rianru(X_fuek,z_fuek,50,100,X_truat,z_truat)จะได้ภาพแบบนี้ ซึ่งเห็นได้ว่าบริเวณสีขาวมีมากขึ้น คือถูกลดค่ากลายเป็น 0 เห็นได้ชัดเจน

นี่แสดงให้เห็นถึงลักษณะเด่นของ l1 ที่ว่าจะทำให้เกิดค่าน้ำหนักเป็น 0 มาก
อ้างอิง
https://www.amazon.co.jp/Python機械学習プログラミング-達人データサイエンティストによる理論と実践-impress-top-gearシリーズ-ebook/dp/B01HGIPIAK
https://www.techcrowd.jp/machinelearning/regularization
https://ja.wikipedia.org/wiki/正則化
https://medium.com/@ken90242/學習日記-c05b8ba3b36f
http://blog.fukuball.com/lin-xuan-tian-jiao-shou-ji-qi-xue-xi-ji-shi-machine-learning-foundations-di-shi-si-jiang-xue-xi-bi-ji
https://morvanzhou.github.io/tutorials/machine-learning/ML-intro/3-09-l1l2regularization
https://www.techcrowd.jp/machinelearning/regularization
https://ja.wikipedia.org/wiki/正則化
https://medium.com/@ken90242/學習日記-c05b8ba3b36f
http://blog.fukuball.com/lin-xuan-tian-jiao-shou-ji-qi-xue-xi-ji-shi-machine-learning-foundations-di-shi-si-jiang-xue-xi-bi-ji
https://morvanzhou.github.io/tutorials/machine-learning/ML-intro/3-09-l1l2regularization
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib