[python] วิเคราะห์แบ่งกลุ่มข้อมูลด้วยวิธีการเพื่อนบ้านใกล้สุด k ตัว (KNN)
เขียนเมื่อ 2017/10/28 19:56
แก้ไขล่าสุด 2022/07/21 14:56
ที่ผ่านมาก่อนหน้านี้ได้เขียนบทความที่เกี่ยวกับการวิเคราะห์แบ่งกลุ่มด้วยวิธีการถดถอยโลจิสติกและเนื้อหาที่เกี่ยวข้องไปหลายตอนด้วยกัน
ที่จริงแล้วเทคนิคการเรียนรู้ของเครื่องนั้นยังมีวิธีอื่นอีกหลายอย่าง ดังนั้นคราวนี้จึงอยากแนะนำเทคนิคที่เรียกว่า วิธีการเพื่อนบ้านใกล้สุด k ตัว (K-近邻算法, k-nearest neighbor, มักย่อเป็น KNN) ซึ่งเป็นวิธีที่อาจถือได้ว่าเข้าใจง่ายที่สุด
หลักการของวิธีการเพื่อนบ้านใกล้สุดนี้ใช้ความคล้ายคลึงหรือใกล้ชิดเป็นตัวตัดสินการแบ่งกลุ่ม
ความคล้ายคลึงใกล้ชิดในที่นี้คืออะไร เพื่อให้เห็นภาพชัดขอเริ่มจากการยกตัวอย่างจะเข้าใจได้ง่ายกว่า
เริ่มจาก สมมุติว่ามีฝูงมด ๓ ชนิดยืนอยู่ตามแหน่งนี้
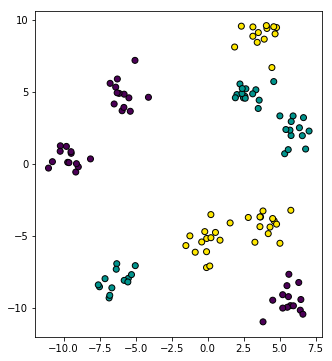
โดยสีแสดงถึงชนิดของมด โดยแบ่งออกเป็น ๓ สายพันธุ์ มดเขียว มดเหลือง มดม่วง
ข้อมูลและภาพนี้สามารถสร้างได้ด้วยการเขียนโค้ดตามนี้ (ข้อมูลกลุ่มก้อนสร้างโดยใช้คำสั่ง make_blobs รายละเอียด https://phyblas.hinaboshi.com/20161127)
ทีนี้หากเราสุ่มตำแหน่งขึ้นมาสักที่ เราจะรู้ได้ยังไงว่าตำแหน่งตรงนั้นเป็นเขตของมดชนิดไหน?
โจทย์ข้อนี้หากใช้การถดถอยโลจิสติกย่อมไม่มีทางหาคำตอบได้ เพราะจุดอ่อนของวิธีนั้นก็คือแบ่งได้เป็นเส้นตรงเท่านั้น แต่หากการกระจายตัวเป็นไปอย่างซับซ้อนแบบนี้ย่อมทำไม่ได้
แต่วิธีการเพื่อนบ้านใกล้สุด k ตัวเป็นวิธีที่สามารถแบ่งกลุ่มได้ไม่ว่าเส้นแบ่งจะซับซ้อนแค่ไหนก็ตาม
วิธีการก็คือ ดูว่าตรงไหนที่อยู่ใกล้ชนิดไหนมากก็แสดงว่าเป็นอาณาเขตของมดชนิดนั้นเลย
การวัดระยะก็ทำได้ง่าย กรณีเป็นพื้นที่สองมิติอย่างในตัวอย่างนี้ก็ (x**2+y**2)**0.5 คำนวณระยะระหว่างตำแหน่งที่เราพิจารณาอยู่กับจุดทุกจุดแล้วหาว่าจุดไหนใกล้สุด จุดนั้นเป็นสีอะไร เท่านี้ก็ได้คำตอบ
ว่าแล้วก็เริ่มจากลองดูตัวอย่างง่ายๆ
เพียงแต่ว่าหากใช้ค่าเดียวแบบนี้ออกจะดูหยาบไปหน่อย เพราะบางทีอาจจะแค่บังเอิญไปใกล้จุดนี้ แต่ที่ใกล้เป็นอันดับ ๒ ๓ ๔ กลับเป็นอีกกลุ่มหนึ่งหมดเลย แบบนั้นก็เป็นไปได้
จำนวนที่นิยมใช้กันมากที่สุดก็คือ ๕ ตัว คือตัดสินว่า ๕ ตัวที่ใกล้ที่สุดเป็นกลุ่มไหนอยู่กี่ตัว กลุ่มไหนมากที่สุดคำตอบก็คือกลุ่มนั้น
การหาจุดที่ใกล้สุดเป็นอันดับต้นๆอาจใช้คำสั่ง argsort
ได้
ต่อมาลองสุ่มจุดในบริเวณนี้มาสัก ๑๕ จุด แล้วหากลุ่มของแต่ละจุด
เพื่อความรวดเร็วควรทำให้สามารถป้อนค่าตำแหน่งหลายจุดเป็นอาเรย์คำนวณพร้อมกันได้ เขียนใหม่ได้ดังนี้
นำมาวาดภาพ โดยจุดที่ทำนายกลุ่มให้เป็นสี่เหลี่ยมขอบแดง ถูกแบ่งกลุ่มตรงกับจุดกลมที่อยู่ใกล้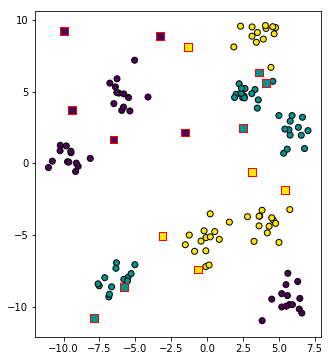
เพื่อความเป็นระเบียบใช้งานสะดวก ต่อไปจะลองทำให้อยู่ในรูปแบบของคลาส เป็นแบบนี้
ในที่นี้เขียนในลักษณะคล้ายกับคลาสของการถดถอยโลจิสติกที่แนะนำไปแล้ว (ดูได้ใน https://phyblas.hinaboshi.com/20171006)
เพียงแต่จะเห็นว่าเมธอดที่เป็นการเรียนรู้นั้นจะเป็นแค่การรับข้อมูลมาเก็บไว้เท่านั้น แต่ที่จะหนักจริงๆคือตอนคำนวณทำนายค่าคำตอบ
จากลักษณะตรงนี้จะเห็นว่าวิธีนี้ต่างจากการถดถอยโลจิสติกมาก เพราะการถดถอยโลจิสติกนั้นพอได้รับข้อมูลมาจะเอาไปคำนวณพารามิเตอร์ค่าน้ำหนัก จากนั้นเวลาจะทำนายค่าก็แค่เอาค่ำน้ำหนักนั้นมาคำนวณ ส่วนค่าข้อมูลที่ใช้เรียนรู้จะทิ้งไปก็ได้ ประมาณว่าเรียนเสร็จความรู้อยู่ในหัวแล้วก็เผาตำราได้เลย
แต่วิธีการเพื่อนบ้านใกล้สุด k ตัวจะต้องเก็บข้อมูลที่ป้อนเข้ามาเอาไว้เป็นตัวเปรียบเทียบตำแหน่งเพื่อใช้คำนวณระยะทางแล้วหาว่าอันไหนใกล้สุดเพื่อจะทำนาย ดังนั้นจะทิ้งข้อมูลไม่ได้
มีชื่อเรียกแบ่งประเภทการเรียนรู้แบบนี้ว่าเป็น นอนพาราเมทริก (nonparametric) คือไม่ใช้พารามิเตอร์ แต่การถดถอยโลจิสติกเป็นแบบพาราเมทริก (parametric)
การถดถอยโลจิสติกเป็นตัวอย่างของอัลกอริธึมในรูปแบบที่ต้องมีการป้อนข้อมูลเรียนรู้เพื่อให้โปรแกรมทำการคำนวณซ้ำๆเพื่อปรับค่าพารามิเตอร์ความชันไปเรื่อย
แต่วิธีการเพื่อนบ้านใกล้สุด k ตัวต่างไปจากการถดถอยโลจิสติกโดยสิ้นเชิง เนื่องจากว่าไม่ต้องมีการสร้างพารามิเตอร์อะไรขึ้นมา
ในโค้ดยังมีส่วนที่น่าขยายความถึงอีกคือตรงส่วนก้อน ((Xn[None]-self.X[:,None])**2).sum(2) ตรงนี้เป็นเทคนิคที่ทำให้สร้างอาเรย์สามมิติซึ่งทำให้คำนวณได้เร็ว แต่มีข้อควรระวังว่าถ้าหากอาเรย์ใหญ่เกินไปจะกลับทำให้ช้าลงได้ ดังนั้นไม่เหมาะจะใช้กับข้อมูลขนาดใหญ่
ลองนำมาใช้ดู โดยคราวนี้สร้างข้อมูลเป็น ๔ กลุ่ม สุ่มหาค่าของจุดในบริเวณดูสัก ๒๐ จุด แล้วก็ลองทำการระบายสีพื้นที่เพื่อให้เห็นอาณาเขตชัดเจนไปด้วย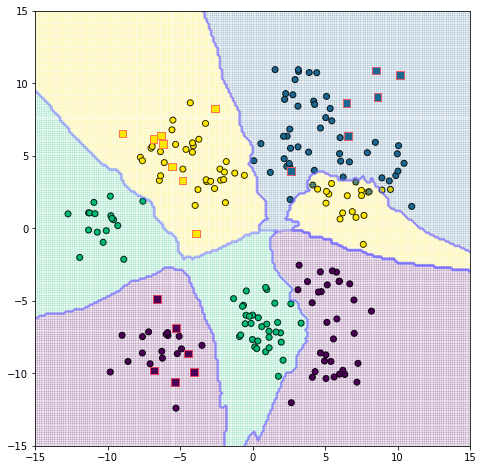
น่าสังเกตว่ามีบางส่วนที่ถูกแบ่งผิดเนื่องจากไปอยู่ท่ามกลางดงของกลุ่มอื่น คือจุดสีเหลืองและน้ำเงินทางขวา เนื่องจากบริเวณนั้นมีการปนซ้อนทับกัน
แต่หากเปลี่ยนจำนวนเพื่อนบ้านเป็น 1 (nk = 1) แล้วดูใหม่จะเป็นแบบนี้
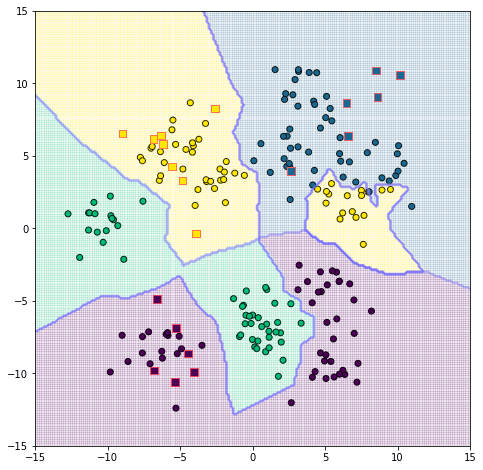
จะเห็นว่าเส้นขีดแบ่งลัดเลาะไปมาแบบดูจงใจกว่าเดิมมาก และตรงจุดที่เป็นตัวข้อมูลฝึกจะไม่มีการถูกแบ่งผิด เพราะที่ใกล้ตัวจุดนั้นเองที่สุดก็คือตัวมันเองอยู่แล้ว
แต่พอเพื่อนบ้านมี 3 ขึ้นไป หากจุดอื่นที่เหลือที่อยู่ใกล้เป็นกลุ่มอื่นก็เท่ากับว่าจุดนั้นโดยจัดไปอยู่กลุ่มอื่นทันที
ดังนั้นเห็นได้ว่าค่าจำนวนเพื่อนบ้านที่พิจารณานั้นมีผลต่อผลลัพธ์
บางทีการที่มีสมาชิกเดียวของกลุ่มหนึ่งอยู่ท่ามกลางดงของกลุ่มอื่นนั้นอาจแค่เพราะจุดนั้นเป็นข้อยกเว้นพิเศษหรือมีปัจจัยบางอย่างที่ไม่คาดคิดก็เป็นได้ ดังนั้นจะให้ใช้จุดนั้นจุดเดียวเป็นตัวพิจารณาก็อาจไม่ใช่ทางเลือกที่ดี อาจทำให้เกิดการเรียนรู้เกิน (over-learning) ได้ง่าย


แต่ก็ไม่ได้หมายความว่าเลือกจำนวนเพื่อนบ้านเยอะแล้วจะดี ยังไงก็ควรเลือกให้เหมาะสมตามกรณี
โดยรวมแล้วก็จะเห็นได้ว่าวิธีการนี้โดยหลักการแล้วดูเข้าใจได้ง่ายดี แค่พิจารณาระยะห่าง
แต่ก็มีข้อควรระวังอยู่เล็กน้อย ที่สำคัญที่สุดก็คือ "ระยะห่าง" ในที่นี้หมายถึงอะไร
จากตัวอย่างข้างต้นนั้นเพื่อให้เห็นภาพชัดจึงให้ระยะทางในที่นี้เป็นระยะทางบนพื้นที่จับต้องได้จริงๆ
แต่ในการคำนวณทั่วไประยะทางที่ว่านี้คือค่าตัวแปรต่างๆที่อาจเป็นอะไรก็ได้
เช่นสมมุติว่าทำนายการงอกของต้นไม้ชนิดหนึ่งโดยดูจากตัวแปรที่นำมาใช้คิดก็อาจเป็นอุณหภูมิและความชื้น
หรือจะแบ่งกลุ่มคนจากคุณสมบัติเช่นส่วนสูงและน้ำหนัก
ปริมาณที่เป็นคนละหน่วยกันแบบนั้นไม่น่าจะเอามาเปรียบเทียบกันได้
ไม่เช่นนั้นคนสูง 1.6 ม. หนัก 50 กก. จะดูใกล้เคียงกับคนสูง 1.8 ม. หนัก 50 กก. พอๆกับคนสูง 1.6 ม. หนัก 50.2 กก. เพราะหากคิดระยะห่างแล้วก็คือ 0.2 เท่ากัน ?? แน่นอนว่าคงจะดูแปลก
กรณีแบบนี้จึงควรมีการทำข้อมูลให้เป็นมาตรฐาน เช่นเดียวกับที่ทำในการถดถอยโลจิสติก แม้ว่าจะเนื่องมาจากคนละเหตุผลกันก็ตาม
เกี่ยวกับเรื่องนี้ได้เขียนถึงไว้แล้วใน https://phyblas.hinaboshi.com/20161124
สามารถเอามาประยุกต์ใช้กับวิธีการเพื่อนบ้านใกล้สุด k ตัวได้เช่นกัน
การทำข้อมูลให้เป็นมาตรฐานจะทำให้ความสำคัญของตัวแปรต่างๆเป็นไปตามการกระจายของข้อมูล ช่วยให้เกณฑ์การหาระยะเป็นไปอย่างเหมาะสมขึ้น
เช่นถ้ากลุ่มคนที่พิจารณามีส่วนสูง 1.4~1.8 หนัก 40~80 แบบนี้ก็จะเท่ากับว่าความต่างส่วนสูง 0.4 สำคัญพอๆกับความต่างน้ำหนัก 40 เวลานำมาคิดระยะห่างก็จะได้ผลออกมาเป็นธรรมชาติมากกว่า
เพื่อให้เห็นภาพ ขอยกตัวอย่าง เช่น มีสัตว์ชนิดหนึ่ง ตัวผู้กับตัวเมียดูเผินๆหน้าตาเหมือนกันมากแยกไม่ออก แต่ว่าน้ำหนักและส่วนสูงมีแนวโน้มต่างกันอยู่เล็กน้อย เมื่อลองนำมาชั่งและวัดดูก็พบการกระจายตามนี้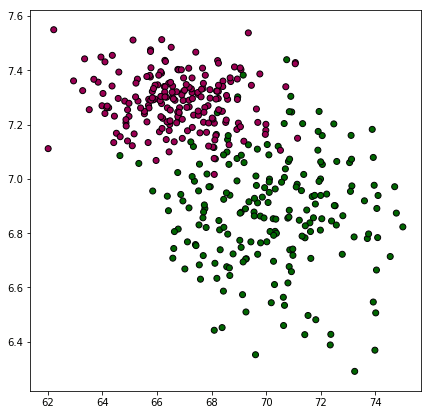
ลองเอามาแบ่งกลุ่มดู หาขอบเขตแบ่งระหว่างตัวผู้กับตัวเมียในปริภูมิของน้ำหนักและส่วนสูง โดยเปรียบเทียบระหว่างทำให้เป็นมาตรฐานแล้วกับยังไม่ได้ทำ
จะเห็นว่าภาพแรกซึ่งยังไม่ได้ทำให้เป็นมาตรฐานนั้นเส้นแบ่งจะค่อนข้างวางตัวในแนวตั้ง นั่นเพราะส่วนสูงมีผลมากกว่าอย่างเห็นได้ชัด ส่วนภาพหลังปรับสัดส่วนแล้ว จึงเห็นว่าแบ่งตามระยะที่ดูสมเหตุสมผลดีกว่า
อีกเรื่องที่ต้องคิดก็ยังมีเรื่องของวิธีการคิดระยะทาง ซึ่งโดยทั่วไปแล้วจะคิดโดยผลรวมกำลังสอง แต่ในบางกรณีก็อาจใช้หลักการคิดระยะแบบอื่นๆ
อีกคำถามที่น่าคิดก็คือ ถ้ามีจุดจำนวนมากมายเป็นพันๆจะต้องมาคำนวณระยะจุดทั้งหมดนี้เลยหรือ? แบบนั้นเสียเวลาเยอะแน่นอน
ใช่แล้ว ในทางปฏิบัติแล้วที่จริงมีอัลกอริธึมที่ช่วยให้เราไม่ต้องคำนวณระยะทั้งหมด เช่นวิธีที่เรียกว่า KD tree หรือ Ball tree เพียงแต่ว่าค่อนข้างซับซ้อนจึงไม่ขอพูดถึง ในที่นี่แต่ต้องการแนะนำแนวคิดจึงใช้วิธีที่เข้าใจง่าย คือคำนวณทั้งหมด
ในตอนต่อไปจะแนะนำการใช้วิธีนี้ด้วย sklearn ซึ่งช่วยให้สามารถทำได้อย่างง่ายดายขึ้นมาก https://phyblas.hinaboshi.com/20171031
อ้างอิง
ที่จริงแล้วเทคนิคการเรียนรู้ของเครื่องนั้นยังมีวิธีอื่นอีกหลายอย่าง ดังนั้นคราวนี้จึงอยากแนะนำเทคนิคที่เรียกว่า วิธีการเพื่อนบ้านใกล้สุด k ตัว (K-近邻算法, k-nearest neighbor, มักย่อเป็น KNN) ซึ่งเป็นวิธีที่อาจถือได้ว่าเข้าใจง่ายที่สุด
หลักการของวิธีการเพื่อนบ้านใกล้สุดนี้ใช้ความคล้ายคลึงหรือใกล้ชิดเป็นตัวตัดสินการแบ่งกลุ่ม
ความคล้ายคลึงใกล้ชิดในที่นี้คืออะไร เพื่อให้เห็นภาพชัดขอเริ่มจากการยกตัวอย่างจะเข้าใจได้ง่ายกว่า
เริ่มจาก สมมุติว่ามีฝูงมด ๓ ชนิดยืนอยู่ตามแหน่งนี้

โดยสีแสดงถึงชนิดของมด โดยแบ่งออกเป็น ๓ สายพันธุ์ มดเขียว มดเหลือง มดม่วง
ข้อมูลและภาพนี้สามารถสร้างได้ด้วยการเขียนโค้ดตามนี้ (ข้อมูลกลุ่มก้อนสร้างโดยใช้คำสั่ง make_blobs รายละเอียด https://phyblas.hinaboshi.com/20161127)
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
np.random.seed(10)
n_klum = 3
tamnaeng,klum = datasets.make_blobs(n_samples=120,n_features=2,centers=9,cluster_std=0.8)
klum %= n_klum
plt.figure(figsize=[6,6])
plt.axes(aspect=1)
plt.scatter(tamnaeng[:,0],tamnaeng[:,1],c=klum,edgecolor='k',cmap='viridis')
plt.show()ทีนี้หากเราสุ่มตำแหน่งขึ้นมาสักที่ เราจะรู้ได้ยังไงว่าตำแหน่งตรงนั้นเป็นเขตของมดชนิดไหน?
โจทย์ข้อนี้หากใช้การถดถอยโลจิสติกย่อมไม่มีทางหาคำตอบได้ เพราะจุดอ่อนของวิธีนั้นก็คือแบ่งได้เป็นเส้นตรงเท่านั้น แต่หากการกระจายตัวเป็นไปอย่างซับซ้อนแบบนี้ย่อมทำไม่ได้
แต่วิธีการเพื่อนบ้านใกล้สุด k ตัวเป็นวิธีที่สามารถแบ่งกลุ่มได้ไม่ว่าเส้นแบ่งจะซับซ้อนแค่ไหนก็ตาม
วิธีการก็คือ ดูว่าตรงไหนที่อยู่ใกล้ชนิดไหนมากก็แสดงว่าเป็นอาณาเขตของมดชนิดนั้นเลย
การวัดระยะก็ทำได้ง่าย กรณีเป็นพื้นที่สองมิติอย่างในตัวอย่างนี้ก็ (x**2+y**2)**0.5 คำนวณระยะระหว่างตำแหน่งที่เราพิจารณาอยู่กับจุดทุกจุดแล้วหาว่าจุดไหนใกล้สุด จุดนั้นเป็นสีอะไร เท่านี้ก็ได้คำตอบ
ว่าแล้วก็เริ่มจากลองดูตัวอย่างง่ายๆ
X = np.array([-1.5,6]) # สร้างจุดขึ้นมาจุดหนึ่ง
raya2 = ((tamnaeng-X)**2).sum(1) # คำนวณระยะสู่แต่ละจุดกำลังสอง (ไม่จำเป็นต้องถอดรากเพราะแค่จะใช้เปรียบเทียบ)
i = raya2.argmin() # ดัชนีของจุดที่ระยะน้อยที่สุด
print(klum[i]) # คำตอบ 0เพียงแต่ว่าหากใช้ค่าเดียวแบบนี้ออกจะดูหยาบไปหน่อย เพราะบางทีอาจจะแค่บังเอิญไปใกล้จุดนี้ แต่ที่ใกล้เป็นอันดับ ๒ ๓ ๔ กลับเป็นอีกกลุ่มหนึ่งหมดเลย แบบนั้นก็เป็นไปได้
จำนวนที่นิยมใช้กันมากที่สุดก็คือ ๕ ตัว คือตัดสินว่า ๕ ตัวที่ใกล้ที่สุดเป็นกลุ่มไหนอยู่กี่ตัว กลุ่มไหนมากที่สุดคำตอบก็คือกลุ่มนั้น
การหาจุดที่ใกล้สุดเป็นอันดับต้นๆอาจใช้คำสั่ง argsort
nk = 5 # จำนวนจุดที่จะพิจารณา
raya2 = ((tamnaeng-X)**2).sum(1)
an_thi_klai = raya2.argsort() # หาดัชนีของจุดที่มีค่าใกล้สุดไล่มาเรื่อยๆ
klum_thi_klai = klum[an_thi_klai] # ดูว่าดัชนีที่ว่านี้คือกลุ่มไหนบ้าง
n_nai_klum = np.array([(klum_thi_klai[:nk]==k).sum() for k in range(n_klum)]) # ดูว่า ๕ อันแรกที่ใกล้สุดมีกลุ่มไหนอยู่กี่ตัว
mi_maksut = n_nai_klum.max() # จำนวนมากที่สุดมีเท่าไหร่
maksutmai = n_nai_klum==mi_maksut # ดูว่ากลุ่มนี้มากสุดหรือไม่
for j in range(nk):
k = klum_thi_klai[j]
if(maksutmai[k]):
z = k # ถ้ามากสุดก็ได้คำตอบเป็นกลุ่มนี้
break
print(u'5 กลุ่มใกล้สุด %s\nคำตอบ %d'%(klum_thi_klai[:5],z))ได้
5 กลุ่มใกล้สุด [0 1 1 0 1]
คำตอบ 1ต่อมาลองสุ่มจุดในบริเวณนี้มาสัก ๑๕ จุด แล้วหากลุ่มของแต่ละจุด
n = 15
x = np.random.uniform(tamnaeng[:,0].min(),tamnaeng[:,0].max(),n)
y = np.random.uniform(tamnaeng[:,1].min(),tamnaeng[:,1].max(),n)
X = np.stack([x,y],1)เพื่อความรวดเร็วควรทำให้สามารถป้อนค่าตำแหน่งหลายจุดเป็นอาเรย์คำนวณพร้อมกันได้ เขียนใหม่ได้ดังนี้
nk = 5
raya2 = ((X[None]-tamnaeng[:,None])**2).sum(2)
klum_thi_klai = klum[raya2.argsort(0)]
n_nai_klum = np.stack([(klum_thi_klai[:nk]==k).sum(0) for k in range(n_klum)])
mi_maksut = n_nai_klum.max(0)
maksutmai = (n_nai_klum==mi_maksut)
z = np.empty(n,dtype=int)
for i in range(n):
for j in range(nk):
k = klum_thi_klai[j,i]
if(maksutmai[k,i]):
z[i] = k
breakนำมาวาดภาพ โดยจุดที่ทำนายกลุ่มให้เป็นสี่เหลี่ยมขอบแดง ถูกแบ่งกลุ่มตรงกับจุดกลมที่อยู่ใกล้
plt.figure(figsize=[6,6])
plt.axes(aspect=1)
plt.scatter(tamnaeng[:,0],tamnaeng[:,1],c=klum,edgecolor='k',cmap='viridis')
plt.scatter(x,y,60,c=z,marker='s',edgecolor='r')
plt.show()
เพื่อความเป็นระเบียบใช้งานสะดวก ต่อไปจะลองทำให้อยู่ในรูปแบบของคลาส เป็นแบบนี้
class Phueanban:
def __init__(self,nk):
self.nk = nk # จำนวนเพื่อนบ้านที่จะพิจารณา
def rianru(self,X,z):
self.X = X # เก็บข้อมูลตำแหน่ง
self.z = z # เก็บข้อมูลการแบ่งกลุ่ม
self.n_klum = z.max()+1 # จำนวนกลุ่ม
def thamnai(self,X):
n = len(X) # จำนวนข้อมูลที่จะคำนวณหา
raya2 = ((X[None]-self.X[:,None])**2).sum(2)
klum_thi_klai = self.z[raya2.argsort(0)]
n_nai_klum = np.stack([(klum_thi_klai[:self.nk]==k).sum(0) for k in range(self.n_klum)])
mi_maksut = n_nai_klum.max(0)
maksutmai = (n_nai_klum==mi_maksut)
z = np.empty(n,dtype=int)
for i in range(n):
for j in range(self.nk):
k = klum_thi_klai[j,i]
if(maksutmai[k,i]):
z[i] = k
break
return zในที่นี้เขียนในลักษณะคล้ายกับคลาสของการถดถอยโลจิสติกที่แนะนำไปแล้ว (ดูได้ใน https://phyblas.hinaboshi.com/20171006)
เพียงแต่จะเห็นว่าเมธอดที่เป็นการเรียนรู้นั้นจะเป็นแค่การรับข้อมูลมาเก็บไว้เท่านั้น แต่ที่จะหนักจริงๆคือตอนคำนวณทำนายค่าคำตอบ
จากลักษณะตรงนี้จะเห็นว่าวิธีนี้ต่างจากการถดถอยโลจิสติกมาก เพราะการถดถอยโลจิสติกนั้นพอได้รับข้อมูลมาจะเอาไปคำนวณพารามิเตอร์ค่าน้ำหนัก จากนั้นเวลาจะทำนายค่าก็แค่เอาค่ำน้ำหนักนั้นมาคำนวณ ส่วนค่าข้อมูลที่ใช้เรียนรู้จะทิ้งไปก็ได้ ประมาณว่าเรียนเสร็จความรู้อยู่ในหัวแล้วก็เผาตำราได้เลย
แต่วิธีการเพื่อนบ้านใกล้สุด k ตัวจะต้องเก็บข้อมูลที่ป้อนเข้ามาเอาไว้เป็นตัวเปรียบเทียบตำแหน่งเพื่อใช้คำนวณระยะทางแล้วหาว่าอันไหนใกล้สุดเพื่อจะทำนาย ดังนั้นจะทิ้งข้อมูลไม่ได้
มีชื่อเรียกแบ่งประเภทการเรียนรู้แบบนี้ว่าเป็น นอนพาราเมทริก (nonparametric) คือไม่ใช้พารามิเตอร์ แต่การถดถอยโลจิสติกเป็นแบบพาราเมทริก (parametric)
การถดถอยโลจิสติกเป็นตัวอย่างของอัลกอริธึมในรูปแบบที่ต้องมีการป้อนข้อมูลเรียนรู้เพื่อให้โปรแกรมทำการคำนวณซ้ำๆเพื่อปรับค่าพารามิเตอร์ความชันไปเรื่อย
แต่วิธีการเพื่อนบ้านใกล้สุด k ตัวต่างไปจากการถดถอยโลจิสติกโดยสิ้นเชิง เนื่องจากว่าไม่ต้องมีการสร้างพารามิเตอร์อะไรขึ้นมา
ในโค้ดยังมีส่วนที่น่าขยายความถึงอีกคือตรงส่วนก้อน ((Xn[None]-self.X[:,None])**2).sum(2) ตรงนี้เป็นเทคนิคที่ทำให้สร้างอาเรย์สามมิติซึ่งทำให้คำนวณได้เร็ว แต่มีข้อควรระวังว่าถ้าหากอาเรย์ใหญ่เกินไปจะกลับทำให้ช้าลงได้ ดังนั้นไม่เหมาะจะใช้กับข้อมูลขนาดใหญ่
ลองนำมาใช้ดู โดยคราวนี้สร้างข้อมูลเป็น ๔ กลุ่ม สุ่มหาค่าของจุดในบริเวณดูสัก ๒๐ จุด แล้วก็ลองทำการระบายสีพื้นที่เพื่อให้เห็นอาณาเขตชัดเจนไปด้วย
n_klum = 4
np.random.seed(10)
tamnaeng,klum = datasets.make_blobs(n_samples=200,n_features=2,centers=12,cluster_std=1.4)
klum %= n_klum
plt.figure(figsize=[8,8])
plt.axes(aspect=1)
plt.scatter(tamnaeng[:,0],tamnaeng[:,1],c=klum,edgecolor='k',cmap='viridis')
nk = 5 # จำนวนเพื่อนบ้าน
pb = Phueanban(nk)
pb.rianru(tamnaeng,klum)
# จุดข้อมูลทดสอบ
n = 20
x = np.random.uniform(tamnaeng[:,0].min(),tamnaeng[:,0].max(),n)
y = np.random.uniform(tamnaeng[:,1].min(),tamnaeng[:,1].max(),n)
X = np.stack([x,y],1)
z = pb.thamnai(X)
plt.scatter(x,y,60,c=z,marker='s',edgecolor='#ff6666')
# ระบายสีพื้น
nmesh = 200
mx,my = np.meshgrid(np.linspace(-15,15,nmesh),np.linspace(-15,15,nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = pb.thamnai(mX).reshape(nmesh,nmesh)
plt.pcolormesh(mx,my,mz,alpha=0.1,cmap='viridis')
plt.contour(mx,my,mz,alpha=0.3,colors='#6666ff')
plt.show()
น่าสังเกตว่ามีบางส่วนที่ถูกแบ่งผิดเนื่องจากไปอยู่ท่ามกลางดงของกลุ่มอื่น คือจุดสีเหลืองและน้ำเงินทางขวา เนื่องจากบริเวณนั้นมีการปนซ้อนทับกัน
แต่หากเปลี่ยนจำนวนเพื่อนบ้านเป็น 1 (nk = 1) แล้วดูใหม่จะเป็นแบบนี้

จะเห็นว่าเส้นขีดแบ่งลัดเลาะไปมาแบบดูจงใจกว่าเดิมมาก และตรงจุดที่เป็นตัวข้อมูลฝึกจะไม่มีการถูกแบ่งผิด เพราะที่ใกล้ตัวจุดนั้นเองที่สุดก็คือตัวมันเองอยู่แล้ว
แต่พอเพื่อนบ้านมี 3 ขึ้นไป หากจุดอื่นที่เหลือที่อยู่ใกล้เป็นกลุ่มอื่นก็เท่ากับว่าจุดนั้นโดยจัดไปอยู่กลุ่มอื่นทันที
ดังนั้นเห็นได้ว่าค่าจำนวนเพื่อนบ้านที่พิจารณานั้นมีผลต่อผลลัพธ์
บางทีการที่มีสมาชิกเดียวของกลุ่มหนึ่งอยู่ท่ามกลางดงของกลุ่มอื่นนั้นอาจแค่เพราะจุดนั้นเป็นข้อยกเว้นพิเศษหรือมีปัจจัยบางอย่างที่ไม่คาดคิดก็เป็นได้ ดังนั้นจะให้ใช้จุดนั้นจุดเดียวเป็นตัวพิจารณาก็อาจไม่ใช่ทางเลือกที่ดี อาจทำให้เกิดการเรียนรู้เกิน (over-learning) ได้ง่าย


แต่ก็ไม่ได้หมายความว่าเลือกจำนวนเพื่อนบ้านเยอะแล้วจะดี ยังไงก็ควรเลือกให้เหมาะสมตามกรณี
โดยรวมแล้วก็จะเห็นได้ว่าวิธีการนี้โดยหลักการแล้วดูเข้าใจได้ง่ายดี แค่พิจารณาระยะห่าง
แต่ก็มีข้อควรระวังอยู่เล็กน้อย ที่สำคัญที่สุดก็คือ "ระยะห่าง" ในที่นี้หมายถึงอะไร
จากตัวอย่างข้างต้นนั้นเพื่อให้เห็นภาพชัดจึงให้ระยะทางในที่นี้เป็นระยะทางบนพื้นที่จับต้องได้จริงๆ
แต่ในการคำนวณทั่วไประยะทางที่ว่านี้คือค่าตัวแปรต่างๆที่อาจเป็นอะไรก็ได้
เช่นสมมุติว่าทำนายการงอกของต้นไม้ชนิดหนึ่งโดยดูจากตัวแปรที่นำมาใช้คิดก็อาจเป็นอุณหภูมิและความชื้น
หรือจะแบ่งกลุ่มคนจากคุณสมบัติเช่นส่วนสูงและน้ำหนัก
ปริมาณที่เป็นคนละหน่วยกันแบบนั้นไม่น่าจะเอามาเปรียบเทียบกันได้
ไม่เช่นนั้นคนสูง 1.6 ม. หนัก 50 กก. จะดูใกล้เคียงกับคนสูง 1.8 ม. หนัก 50 กก. พอๆกับคนสูง 1.6 ม. หนัก 50.2 กก. เพราะหากคิดระยะห่างแล้วก็คือ 0.2 เท่ากัน ?? แน่นอนว่าคงจะดูแปลก
กรณีแบบนี้จึงควรมีการทำข้อมูลให้เป็นมาตรฐาน เช่นเดียวกับที่ทำในการถดถอยโลจิสติก แม้ว่าจะเนื่องมาจากคนละเหตุผลกันก็ตาม
เกี่ยวกับเรื่องนี้ได้เขียนถึงไว้แล้วใน https://phyblas.hinaboshi.com/20161124
สามารถเอามาประยุกต์ใช้กับวิธีการเพื่อนบ้านใกล้สุด k ตัวได้เช่นกัน
การทำข้อมูลให้เป็นมาตรฐานจะทำให้ความสำคัญของตัวแปรต่างๆเป็นไปตามการกระจายของข้อมูล ช่วยให้เกณฑ์การหาระยะเป็นไปอย่างเหมาะสมขึ้น
เช่นถ้ากลุ่มคนที่พิจารณามีส่วนสูง 1.4~1.8 หนัก 40~80 แบบนี้ก็จะเท่ากับว่าความต่างส่วนสูง 0.4 สำคัญพอๆกับความต่างน้ำหนัก 40 เวลานำมาคิดระยะห่างก็จะได้ผลออกมาเป็นธรรมชาติมากกว่า
เพื่อให้เห็นภาพ ขอยกตัวอย่าง เช่น มีสัตว์ชนิดหนึ่ง ตัวผู้กับตัวเมียดูเผินๆหน้าตาเหมือนกันมากแยกไม่ออก แต่ว่าน้ำหนักและส่วนสูงมีแนวโน้มต่างกันอยู่เล็กน้อย เมื่อลองนำมาชั่งและวัดดูก็พบการกระจายตามนี้
np.random.seed(0)
sung = np.hstack([np.random.normal(70,2.1,200),np.random.normal(67,1.8,200)])
nak = np.hstack([np.random.normal(6.9,0.2,200),np.random.normal(7.3,0.1,200)])
z = np.hstack([np.zeros(200),np.ones(200)]).astype(int)
plt.figure(figsize=[7,7])
plt.scatter(sung,nak,c=z,edgecolor='k',cmap='PiYG_r')
plt.show()
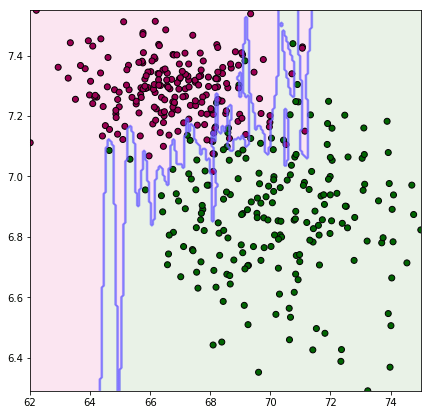
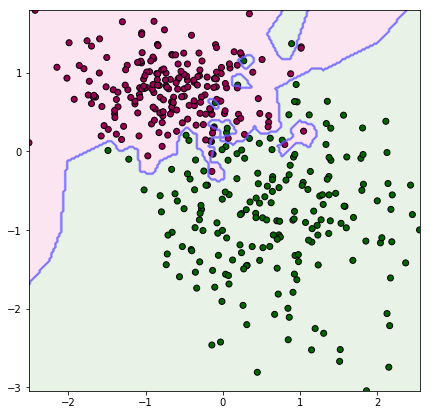
ลองเอามาแบ่งกลุ่มดู หาขอบเขตแบ่งระหว่างตัวผู้กับตัวเมียในปริภูมิของน้ำหนักและส่วนสูง โดยเปรียบเทียบระหว่างทำให้เป็นมาตรฐานแล้วกับยังไม่ได้ทำ
X = np.stack([sung,nak],1)
for i in [0,1]:
if(i==1): # สำหรับรอบที่ 2 ทำให้เป็นมาตรฐาน
X = (X-X.mean(0))/X.std(0)
pb = Phueanban(nk=1)
pb.rianru(X,z)
nmesh = 200
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),nmesh),np.linspace(X[:,1].min(),X[:,1].max(),nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = pb.thamnai(mX).reshape(nmesh,nmesh)
plt.figure(figsize=[7,7])
plt.axes(xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.contourf(mx,my,mz,alpha=0.1,cmap='PiYG_r')
plt.contour(mx,my,mz,alpha=0.3,colors='#6666ff')
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='PiYG_r')
plt.show()

จะเห็นว่าภาพแรกซึ่งยังไม่ได้ทำให้เป็นมาตรฐานนั้นเส้นแบ่งจะค่อนข้างวางตัวในแนวตั้ง นั่นเพราะส่วนสูงมีผลมากกว่าอย่างเห็นได้ชัด ส่วนภาพหลังปรับสัดส่วนแล้ว จึงเห็นว่าแบ่งตามระยะที่ดูสมเหตุสมผลดีกว่า
อีกเรื่องที่ต้องคิดก็ยังมีเรื่องของวิธีการคิดระยะทาง ซึ่งโดยทั่วไปแล้วจะคิดโดยผลรวมกำลังสอง แต่ในบางกรณีก็อาจใช้หลักการคิดระยะแบบอื่นๆ
อีกคำถามที่น่าคิดก็คือ ถ้ามีจุดจำนวนมากมายเป็นพันๆจะต้องมาคำนวณระยะจุดทั้งหมดนี้เลยหรือ? แบบนั้นเสียเวลาเยอะแน่นอน
ใช่แล้ว ในทางปฏิบัติแล้วที่จริงมีอัลกอริธึมที่ช่วยให้เราไม่ต้องคำนวณระยะทั้งหมด เช่นวิธีที่เรียกว่า KD tree หรือ Ball tree เพียงแต่ว่าค่อนข้างซับซ้อนจึงไม่ขอพูดถึง ในที่นี่แต่ต้องการแนะนำแนวคิดจึงใช้วิธีที่เข้าใจง่าย คือคำนวณทั้งหมด
ในตอนต่อไปจะแนะนำการใช้วิธีนี้ด้วย sklearn ซึ่งช่วยให้สามารถทำได้อย่างง่ายดายขึ้นมาก https://phyblas.hinaboshi.com/20171031
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib