การทำเครื่องเวกเตอร์ค้ำยัน (SVM) โดยใช้ sklearn
เขียนเมื่อ 2018/07/12 18:04
แก้ไขล่าสุด 2022/07/19 05:49
ในบทความที่แล้วได้เขียนหลักการของเครื่องเวกเตอร์ค้ำยัน (support vector machine) หรือ SVM ไปแล้ว https://phyblas.hinaboshi.com/20180709
แม้โปรแกรมสำหรับสร้าง SVM นั้นค่อนข้างซับซ้อน แต่เนื่องจากมีมอดูลที่ได้เขียน SVM ไว้อย่างดีอยู่แล้วอย่าง sklearn ดังนั้นจึงดึงมาใช้ได้เลย
วิธีการคำนวณ SVM ของ sklearn นั้นอาศัยไลบรารีภาษาซีชื่อ LIBSVM ซึ่งถูกพัฒนาขึ้นโดย ศ.หลิน จื้อเหริน (林智仁) แห่งมหาวิทยาลัยแห่งชาติไต้หวัน (國立台灣大學) ทำให้มีความรวดเร็วสูง เหมาะกับการใช้งานจริงมากกว่าโปรแกรมที่เขียนขึ้นเองจากไพธอนล้วนๆ
การใช้งานเบื้องต้น
SVM ภายใน sklearn อยู่ในมอดูลย่อย sklearn.svm ในนี้มีคลาสของ SVM อยู่หลายตัว แต่ที่เป็นพื้นฐานที่จะแนะนำตรงนี้คือ SVC (ย่อมาจาก support vector classifier) ซึ่งเป็นคลาสสำหรับ SVM ที่ใช้ทั่วไปมากที่สุด สามารถใช้เคอร์เนลชนิดไหนก็ได้
นอกจากนี้ยังมี LinearSVC ซึ่งมีไว้ใช้ SVM เชิงเส้นโดยเฉพาะอยู่ด้วย ที่จริง SVC สามารถใช้เคอร์เนลเชิงเส้นได้อยู่แล้ว แต่เนื่องจากอัลกอริธึมต่างกัน หากใช้ LinearSVC จะเร็วกว่า
โดยค่าตั้งต้นแล้ว SVC จะใช้เคอร์เนลชนิด RBF หากไม่ได้มีการระบุชนิดเคอร์เนลลงไป
ตัวอย่างการใช้ ให้ SMC เรียนรู้จากข้อมูลที่ป้อนเข้าไปแล้วให้ทำนายผลการแบ่งที่จุดต่างๆแล้วสร้างเป็นคอนทัวร์แสดงการแบ่งเขต
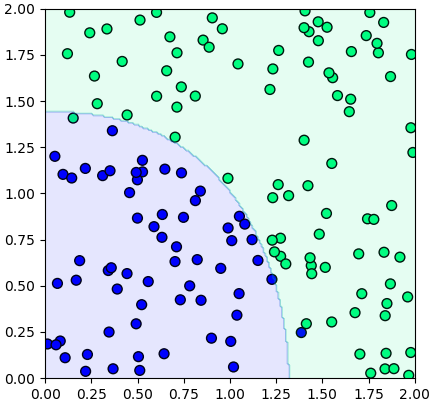
จะเห็นว่าแบ่งออกมาเป็นเส้นโค้งได้ดี
หากต้องการใช้เคอร์เนลชนิดอื่นก็สามารถระบุชื่อชนิดเคอร์เนลลงไปตอนสร้างได้ เคอร์เนลที่ใช้ใน SVC ได้คือ
- 'linear' เชิงเส้น
- 'poly' พหุนาม
- 'rbf'
- 'sigmoid'
- 'precomputed' ใช้ค่าที่คำนวณโดยเคอร์เนลที่เตรียมเองเอาไว้แล้ว
นอกจากนี้ยังสามารถนิยามฟังก์ชันเคอร์เนลใส่ลงไปเองได้ โดยใส่ฟังก์ชันที่ต้องการลงไป
ต่อไปลองเทียบเคอร์เนลแบบต่างๆ
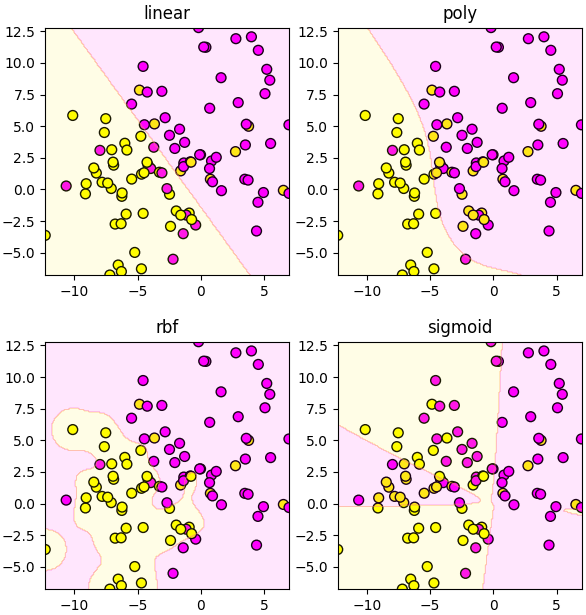
ข้อมูลในตัวอย่างนี้ถูกสร้างโดยคำสั่ง make_blobs ซึ่งแนะนำไปใน https://phyblas.hinaboshi.com/20161127
ปรับไฮเพอร์พารามิเตอร์
ตัวอย่างที่เพิ่งยกไปนั้นเป็นการสร้างขึ้นใช้อย่างง่ายโดยใช้ค่าทุกอย่างเป็นพื้นฐาน ไม่ได้ปรับอะไร แต่ SVC นั้นมีค่าหลายอย่างที่สามารถปรับได้
ที่สำคัญที่สุดคือค่า C ซึ่งเป็นตัวกำหนดขนาดของเรกูลาไรซ์
นอกจากนี้ยังมีพารามิเตอร์ตามแต่ละชนิดของเคอร์เนล ซึ่งสำหรับกรณีของ RBF แล้วก็จะมี gamma () คือส่วนกลับของอัตราการลดค่าตามระยะห่างจากใจกลาง
ถ้าไม่ได้ระบุ ค่าพารามิเตอร์จะเป็นค่าตั้งต้น คือ C=1 ส่วน gamma จะถูกเลือกโดยอัตโนมัติเป็น 1/จำนวนตัวแปร
การเลือกพารามิเตอร์ที่เหมาะสมกับปัญหาก็มีความสำคัญ เพราะมีผลกับผลลัพธ์ที่ได้มาก
ตัวอย่างแสดงการเปลี่ยนค่าพารามิเตอร์และเปรียบเทียบ ข้อมูลสร้างโดยคำสั่ง make_moons ซึ่งแนะนำไปใน https://phyblas.hinaboshi.com/20171202
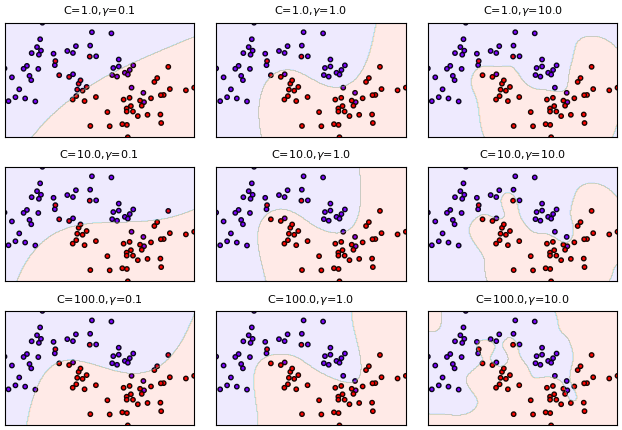
จะเห็นได้ว่ายิ่งค่า gamma หรือ C มากก็ยิ่งทำให้รูปร่างซับซ้อนมากขึ้น ปรับเส้นแบ่งเข้ากับข้อมูลที่ป้อนเข้าไปได้มากขึ้น แต่ก็มีแนวโน้มจะทำให้เกิดการเรียนรู้เกิน
ลองหาค่า C ที่เหมาะสมด้วยการใช้ validation_curve ตามวิธีที่เขียนไปใน https://phyblas.hinaboshi.com/20171020
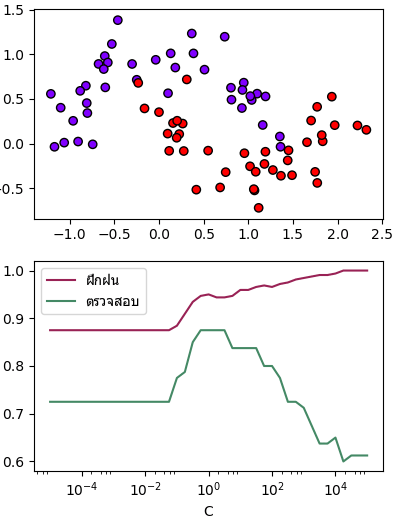
ผลที่ได้จะเห็นว่าค่าที่เหมาะสมที่ทำให้ทายข้อมูลตรวจสอบได้มากที่สุดอยู่ที่ประมาณ 1 ถ้ามากไปก็จะเรียนรู้เกิน ถ้าน้อยไปก็จะเรียนรู้ไม่พอ
ฟังก์ชันตัดสิน
ฟังก์ชันตัดสิน (决策函数, decision function) คือฟังก์ชันที่จะกำหนดผลการทำนายแบ่งกลุ่มโดยค่ามากกว่า 0 เป็นกลุ่มนึง น้อยกว่า 0 เป็นอีกกลุ่ม ฟังก์ชันตัดสินใจคำนวณจากเคอร์เนลและตัวคูณลากรองจ์ตามสมการ (4.2) ในบทความที่แล้ว
สำหรับใน SVC ของ sklearn สามารถคำนวณฟังก์ชันตัดสินได้โดยใช้เมธอด .decision_function() วิธีใช้เหมือนกับการใช้ .predict() เพื่อทำนาย แต่ผลที่ได้จะเป็นค่าฟังก์ชันค่าต่อเนื่อง ไม่ใช่ผลการแบ่ง
ตัวอย่าง ลองสร้างคอนทัวร์แสดงค่าฟังก์ชันตัดสินที่จุดต่างๆ
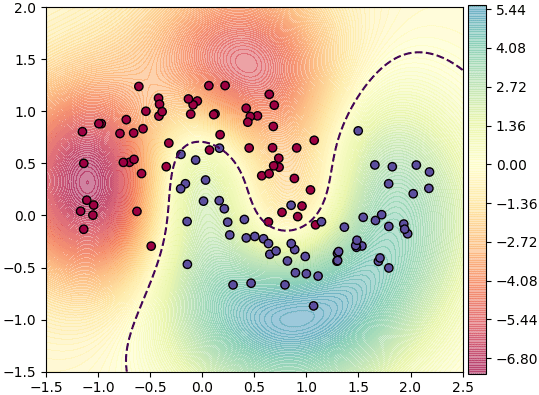
การแบ่งมากกว่า ๒ กลุ่ม
หลักการทำงานของ SVM คือสร้างเส้นกั้นระหว่างกลุ่มข้อมูล ๒ กลุ่ม ดังนั้นโดยพื้นฐานแล้วมีไว้แบ่งกลุ่มข้อมูลแค่ ๒ กลุ่มออกจากกัน
แต่วิธีการนี้ก็ยังสามารถต่อยอดเพื่อแบ่งกลุ่มข้อมูลกี่กลุ่มก็ได้ วิธีการก็คือจับคู่แบ่งทีละคู่ แล้วเทียบผลลัพธ์ทั้งหมด ดูว่าอันไหนมีค่ารวมสูงสุดในจุดนั้นๆ
เวลาที่ใช้ SVC ใน sklearn หากข้อมูลที่ป้อนเข้าไปมีมากกว่า ๒ กลุ่ม โปรแกรมจะทำการสร้าง SVM มากกว่าหนึ่งตัวขึ้นให้ภายในโดยอัตโนมัติ ทำให้สามารถแบ่งหลายกลุ่มได้โดยไม่ต้องทำอะไรเพิ่มเติมเอง
ตัวอย่างกรณีแบ่งหลายกลุ่ม
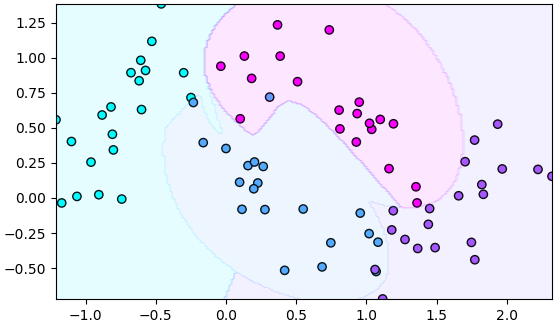
จะเห็นว่าสามารถแบ่งออกมาได้เช่นกัน
แม้จะคำนวณออกมาได้ดูเผินๆไม่ต่างจากกรณีแบ่ง ๒ กลุ่ม แต่ว่าจริงๆกลไกภายในเพิ่มความซับซ้อนขึ้นไปกว่า มีรายละเอียดเพิ่มเติมพอสมควร
เช่น เวลาที่คำนวณฟังก์ชันตัดสิน จะพบว่าผลที่ได้ออกมาเป็นอาเรย์สองมิติ ซึ่งเป็นผลจากการเทียบกลุ่มนึงกับกลุ่มที่เหลือ ดังนั้นจึงได้อาเรย์ขนาด (จำนวนจุดข้อมูล, จำนวนตัวแปร)
ลองแสดงค่าฟังก์ชันตัดสินทั้ง ๔ อันออกมาดูได้ดังนี้
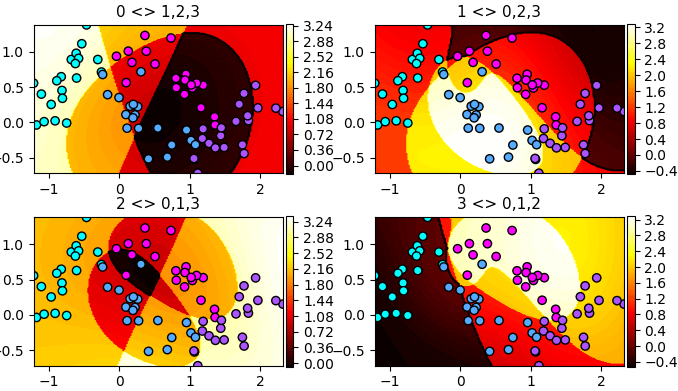
จะเห็นว่าบริเวณที่มีค่ามากจนเป็นสีขาวๆในแต่ละภาพคือบริเวณที่ถูกแบ่งให้เป็นของกลุ่มนั้น รูปร่างที่ออกมาดูเหมือนมีจุดตัดมากมายนั่นที่จริงก็เกิดจากการแบ่งด้วยเส้นโค้งหลายเส้นตัดกัน
แต่นอกจากนี้ยังสามารถให้แสดงฟังก์ชันตัดสินใจของกลุ่มหนึ่งเทียบกับอีกกลุ่มหนึ่ง เทียบกันเป็นคู่ๆ
โดยไปปรับที่แอตทริบิวต์ decision_function_shape โดยให้ svc.decision_function_shape = 'ovo'
หรือจะกำหนดให้ชัดตั้งแต่ตอนสร้างออบเจ็กต์ก็ได้ คือเขียนเป็น scv = SVC(decision_function_shape='ovo')
เพียงแค่นี้ พอใช้ .decision_function() ผลที่ได้ก็จะเปลี่ยนไป กลายเป็นแบบที่เทียบกลุ่มหนึ่งกับอีกกลุ่มเป็นคู่ๆ
ซึ่งกรณีแบบนี้จะได้อาเรย์ขนาดเป็น (จำนวนจุดข้อมูล, m*(m-1)/2) โดย m คือจำนวนตัวแปร เช่น กรณีที่มีอยู่ ๔ ตัว ก็จะได้ออกมาเป็น ๖
ลองแสดงฟังก์ชันตัดสินใจทั้ง ๖ ออกมาดู
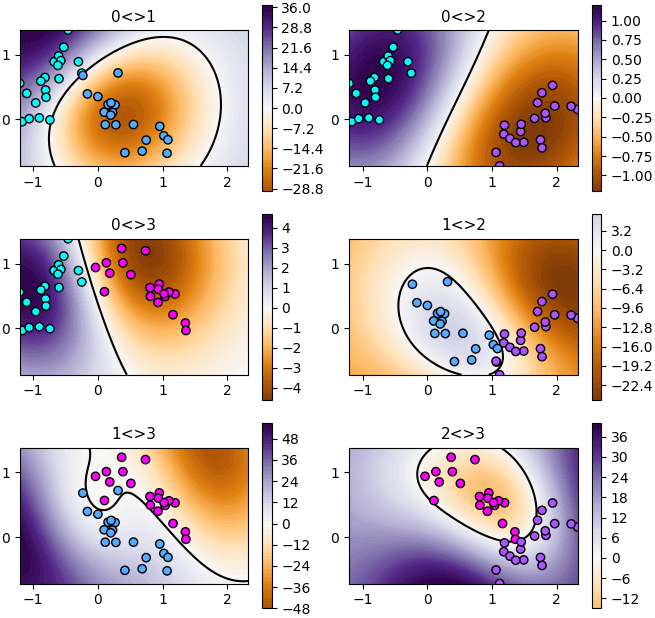
จะเห็นว่าโดยพื้นฐานแล้วภายใน SVC ได้สร้างตัวแบ่งแบบนี้ขึ้นมา ๖ อัน แล้วจึงนำไปแปลงผลเพื่อตัดสินว่าเขตไหนควรเป็นของกลุ่มไหนอีกที
ในทางกลับกันหากต้องการเปลี่ยนกลับเป็นแบบเปรียบเทียบกลุ่มหนึ่งกับกลุ่มที่เหลือก็ใส่ svc.decision_function_shape = 'ovr'
ข้อมูลเวกเตอร์ค้ำยันที่ได้
เมื่อทำการเรียนรู้จากข้อมูลที่ป้อนเข้าไปให้เสร็จ โปรแกรมจะบันทึกไว้ว่าจุดไหนที่ถูกใช้เป็นเวกเตอร์ค้ำยัน และจุดนั้นมีค่าตัวคูณลากรองจ์เป็นเท่าไหร่
.support_ คือ ดัชนีของตัวที่เป็นเวกเตอร์ค้ำยัน
.support_vectors_ คือ ค่าตำแหน่ง
.dual_coef_ คือ ตัวคูณลากรองจ์คูณกับคำตอบจริง (a*z)
dual_coef_ นั้นบ่งบอกถึงความสำคัญของเวกเตอร์ค้ำยันตัวนั้น ยิ่งห่างจากศูนย์มากก็ยิ่งมีผลต่อการคำนวณมาก
ลองใช้ SVC แบ่งกลุ่มเสร็จแล้วหาว่าเวกเตอร์ค้ำยันอยู่ตรงไหนบ้าง โดยแสดงเป็นรูปดาวที่มีขนาดแปรตามขนาดความสำคัญ
จะเห็นว่าเวกเตอร์ค้ำยันมีอยู่จำนวนมากมายยืนอยู่ตามแถบรอบนอกของกลุ่ม
ทั้งหมดนี้เป็นตัวอย่างส่วนหนึ่งของการใช้ SVC ใน sklearn
นอกจากนี้แล้วก็ยังมีรายละเอียดปลีกย่อยและคำสั่งอีกหลายอย่างในนี้ที่ยังไม่ได้แนะนำอยู่ สามารถลองไปศึกษสและใช้กันต่อดูได้
อ้างอิง
แม้โปรแกรมสำหรับสร้าง SVM นั้นค่อนข้างซับซ้อน แต่เนื่องจากมีมอดูลที่ได้เขียน SVM ไว้อย่างดีอยู่แล้วอย่าง sklearn ดังนั้นจึงดึงมาใช้ได้เลย
วิธีการคำนวณ SVM ของ sklearn นั้นอาศัยไลบรารีภาษาซีชื่อ LIBSVM ซึ่งถูกพัฒนาขึ้นโดย ศ.หลิน จื้อเหริน (林智仁) แห่งมหาวิทยาลัยแห่งชาติไต้หวัน (國立台灣大學) ทำให้มีความรวดเร็วสูง เหมาะกับการใช้งานจริงมากกว่าโปรแกรมที่เขียนขึ้นเองจากไพธอนล้วนๆ
การใช้งานเบื้องต้น
SVM ภายใน sklearn อยู่ในมอดูลย่อย sklearn.svm ในนี้มีคลาสของ SVM อยู่หลายตัว แต่ที่เป็นพื้นฐานที่จะแนะนำตรงนี้คือ SVC (ย่อมาจาก support vector classifier) ซึ่งเป็นคลาสสำหรับ SVM ที่ใช้ทั่วไปมากที่สุด สามารถใช้เคอร์เนลชนิดไหนก็ได้
นอกจากนี้ยังมี LinearSVC ซึ่งมีไว้ใช้ SVM เชิงเส้นโดยเฉพาะอยู่ด้วย ที่จริง SVC สามารถใช้เคอร์เนลเชิงเส้นได้อยู่แล้ว แต่เนื่องจากอัลกอริธึมต่างกัน หากใช้ LinearSVC จะเร็วกว่า
โดยค่าตั้งต้นแล้ว SVC จะใช้เคอร์เนลชนิด RBF หากไม่ได้มีการระบุชนิดเคอร์เนลลงไป
ตัวอย่างการใช้ ให้ SMC เรียนรู้จากข้อมูลที่ป้อนเข้าไปแล้วให้ทำนายผลการแบ่งที่จุดต่างๆแล้วสร้างเป็นคอนทัวร์แสดงการแบ่งเขต
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
X = np.random.uniform(0,2,[150,2])
z = (X[:,0]**2+X[:,1]**2)>2
svc = SVC()
svc.fit(X,z)
plt.axes(aspect=1,xlim=[0,2],ylim=[0,2])
plt.scatter(X[:,0],X[:,1],s=50,c=z,edgecolor='k',cmap='winter')
mx,my = np.meshgrid(np.linspace(0,2,200),np.linspace(0,2,200))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = svc.predict(mX).reshape(200,200)
plt.contourf(mx,my,mz,alpha=0.1,cmap='winter')
plt.show()
จะเห็นว่าแบ่งออกมาเป็นเส้นโค้งได้ดี
หากต้องการใช้เคอร์เนลชนิดอื่นก็สามารถระบุชื่อชนิดเคอร์เนลลงไปตอนสร้างได้ เคอร์เนลที่ใช้ใน SVC ได้คือ
- 'linear' เชิงเส้น
- 'poly' พหุนาม
- 'rbf'
- 'sigmoid'
- 'precomputed' ใช้ค่าที่คำนวณโดยเคอร์เนลที่เตรียมเองเอาไว้แล้ว
นอกจากนี้ยังสามารถนิยามฟังก์ชันเคอร์เนลใส่ลงไปเองได้ โดยใส่ฟังก์ชันที่ต้องการลงไป
ต่อไปลองเทียบเคอร์เนลแบบต่างๆ
from sklearn import datasets
X,z = datasets.make_blobs(n_samples=100,n_features=2,cluster_std=4,centers=2,random_state=3)
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),200),np.linspace(X[:,1].min(),X[:,1].max(),200))
mX = np.stack([mx.ravel(),my.ravel()],1)
plt.figure(figsize=[6,7])
kernel = ['linear','poly','rbf','sigmoid']
for i in range(4):
svc = SVC(kernel=kernel[i])
svc.fit(X,z)
mz = svc.predict(mX).reshape(200,200)
plt.subplot(2,2,i+1,aspect=1,xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.scatter(X[:,0],X[:,1],s=50,c=z,edgecolor='k',cmap='spring')
plt.contourf(mx,my,mz,alpha=0.1,cmap='spring')
plt.title(kernel[i])
plt.tight_layout()
plt.show()
ข้อมูลในตัวอย่างนี้ถูกสร้างโดยคำสั่ง make_blobs ซึ่งแนะนำไปใน https://phyblas.hinaboshi.com/20161127
ปรับไฮเพอร์พารามิเตอร์
ตัวอย่างที่เพิ่งยกไปนั้นเป็นการสร้างขึ้นใช้อย่างง่ายโดยใช้ค่าทุกอย่างเป็นพื้นฐาน ไม่ได้ปรับอะไร แต่ SVC นั้นมีค่าหลายอย่างที่สามารถปรับได้
ที่สำคัญที่สุดคือค่า C ซึ่งเป็นตัวกำหนดขนาดของเรกูลาไรซ์
นอกจากนี้ยังมีพารามิเตอร์ตามแต่ละชนิดของเคอร์เนล ซึ่งสำหรับกรณีของ RBF แล้วก็จะมี gamma () คือส่วนกลับของอัตราการลดค่าตามระยะห่างจากใจกลาง
ถ้าไม่ได้ระบุ ค่าพารามิเตอร์จะเป็นค่าตั้งต้น คือ C=1 ส่วน gamma จะถูกเลือกโดยอัตโนมัติเป็น 1/จำนวนตัวแปร
การเลือกพารามิเตอร์ที่เหมาะสมกับปัญหาก็มีความสำคัญ เพราะมีผลกับผลลัพธ์ที่ได้มาก
ตัวอย่างแสดงการเปลี่ยนค่าพารามิเตอร์และเปรียบเทียบ ข้อมูลสร้างโดยคำสั่ง make_moons ซึ่งแนะนำไปใน https://phyblas.hinaboshi.com/20171202
X,z = datasets.make_moons(n_samples=80,shuffle=0,noise=0.25,random_state=0)
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),200),np.linspace(X[:,1].min(),X[:,1].max(),200))
mX = np.stack([mx.ravel(),my.ravel()],1)
plt.figure(figsize=[6.5,4.5])
for i,C in enumerate([1,10,100]):
for j,gamma in enumerate([0.1,1,10]):
svc = SVC(C=C,gamma=gamma)
svc.fit(X,z)
mz = svc.predict(mX).reshape(200,200)
plt.subplot2grid((3,3),(i,j),xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()],xticks=[],yticks=[],aspect=1)
plt.scatter(X[:,0],X[:,1],s=10,c=z,edgecolor='k',cmap='rainbow')
plt.contourf(mx,my,mz,alpha=0.1,cmap='rainbow')
plt.title('C=%.1f,$\\gamma$=%.1f'%(C,gamma),size=8)
plt.tight_layout()
plt.show()
จะเห็นได้ว่ายิ่งค่า gamma หรือ C มากก็ยิ่งทำให้รูปร่างซับซ้อนมากขึ้น ปรับเส้นแบ่งเข้ากับข้อมูลที่ป้อนเข้าไปได้มากขึ้น แต่ก็มีแนวโน้มจะทำให้เกิดการเรียนรู้เกิน
ลองหาค่า C ที่เหมาะสมด้วยการใช้ validation_curve ตามวิธีที่เขียนไปใน https://phyblas.hinaboshi.com/20171020
from sklearn.model_selection import validation_curve
X,z = datasets.make_moons(n_samples=80,shuffle=0,noise=0.2,random_state=0)
ccc = 10**np.linspace(-5,5,41)
khanaen_fuek,khanaen_truat = validation_curve(SVC(gamma=1),X,z,param_name='C',param_range=ccc,cv=5)
plt.figure(figsize=[4.5,6])
plt.subplot(211,aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='rainbow')
plt.subplot(212,xscale='log',xlabel='C')
plt.plot(ccc,np.mean(khanaen_fuek,1),color='#992255')
plt.plot(ccc,np.mean(khanaen_truat,1),color='#448965')
plt.legend([u'ฝึกฝน',u'ตรวจสอบ'],prop={'family':'Tahoma'})
plt.show()
ผลที่ได้จะเห็นว่าค่าที่เหมาะสมที่ทำให้ทายข้อมูลตรวจสอบได้มากที่สุดอยู่ที่ประมาณ 1 ถ้ามากไปก็จะเรียนรู้เกิน ถ้าน้อยไปก็จะเรียนรู้ไม่พอ
ฟังก์ชันตัดสิน
ฟังก์ชันตัดสิน (决策函数, decision function) คือฟังก์ชันที่จะกำหนดผลการทำนายแบ่งกลุ่มโดยค่ามากกว่า 0 เป็นกลุ่มนึง น้อยกว่า 0 เป็นอีกกลุ่ม ฟังก์ชันตัดสินใจคำนวณจากเคอร์เนลและตัวคูณลากรองจ์ตามสมการ (4.2) ในบทความที่แล้ว
สำหรับใน SVC ของ sklearn สามารถคำนวณฟังก์ชันตัดสินได้โดยใช้เมธอด .decision_function() วิธีใช้เหมือนกับการใช้ .predict() เพื่อทำนาย แต่ผลที่ได้จะเป็นค่าฟังก์ชันค่าต่อเนื่อง ไม่ใช่ผลการแบ่ง
ตัวอย่าง ลองสร้างคอนทัวร์แสดงค่าฟังก์ชันตัดสินที่จุดต่างๆ
X,z = datasets.make_moons(n_samples=120,shuffle=0,noise=0.2,random_state=2)
svc = SVC(C=1e2,gamma=1)
svc.fit(X,z)
plt.axes(aspect=1)
mX = np.stack(np.meshgrid(np.linspace(-1.5,2.5,200),np.linspace(-1.5,2,200)),2)
mz = svc.decision_function(mX.reshape(-1,2)).reshape(200,-1)
vmax = np.abs(mz).max()
plt.contourf(mX[:,:,0],mX[:,:,1],mz,200,alpha=0.5,cmap='Spectral',vmin=-vmax,vmax=vmax)
plt.colorbar(pad=0.01)
plt.contour(mX[:,:,0],mX[:,:,1],mz,[0],linestyles='--')
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='Spectral')
plt.show()
การแบ่งมากกว่า ๒ กลุ่ม
หลักการทำงานของ SVM คือสร้างเส้นกั้นระหว่างกลุ่มข้อมูล ๒ กลุ่ม ดังนั้นโดยพื้นฐานแล้วมีไว้แบ่งกลุ่มข้อมูลแค่ ๒ กลุ่มออกจากกัน
แต่วิธีการนี้ก็ยังสามารถต่อยอดเพื่อแบ่งกลุ่มข้อมูลกี่กลุ่มก็ได้ วิธีการก็คือจับคู่แบ่งทีละคู่ แล้วเทียบผลลัพธ์ทั้งหมด ดูว่าอันไหนมีค่ารวมสูงสุดในจุดนั้นๆ
เวลาที่ใช้ SVC ใน sklearn หากข้อมูลที่ป้อนเข้าไปมีมากกว่า ๒ กลุ่ม โปรแกรมจะทำการสร้าง SVM มากกว่าหนึ่งตัวขึ้นให้ภายในโดยอัตโนมัติ ทำให้สามารถแบ่งหลายกลุ่มได้โดยไม่ต้องทำอะไรเพิ่มเติมเอง
ตัวอย่างกรณีแบ่งหลายกลุ่ม
X,y = datasets.make_moons(n_samples=80,shuffle=0,noise=0.2,random_state=0)
y[60:] = 2
y[:20] = 3
svc = SVC(C=1e4)
svc.fit(X,y)
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),200),np.linspace(X[:,1].min(),X[:,1].max(),200))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = svc.predict(mX).reshape(200,200)
plt.axes(aspect=1,xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.scatter(X[:,0],X[:,1],c=y,edgecolor='k',cmap='cool')
plt.contourf(mx,my,mz,alpha=0.1,cmap='cool')
plt.show()
จะเห็นว่าสามารถแบ่งออกมาได้เช่นกัน
แม้จะคำนวณออกมาได้ดูเผินๆไม่ต่างจากกรณีแบ่ง ๒ กลุ่ม แต่ว่าจริงๆกลไกภายในเพิ่มความซับซ้อนขึ้นไปกว่า มีรายละเอียดเพิ่มเติมพอสมควร
เช่น เวลาที่คำนวณฟังก์ชันตัดสิน จะพบว่าผลที่ได้ออกมาเป็นอาเรย์สองมิติ ซึ่งเป็นผลจากการเทียบกลุ่มนึงกับกลุ่มที่เหลือ ดังนั้นจึงได้อาเรย์ขนาด (จำนวนจุดข้อมูล, จำนวนตัวแปร)
ลองแสดงค่าฟังก์ชันตัดสินทั้ง ๔ อันออกมาดูได้ดังนี้
plt.figure(figsize=[7,4])
df = svc.decision_function(mX).reshape(200,200,-1)
for i in range(4):
plt.subplot(2,2,i+1,aspect=1,xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.scatter(X[:,0],X[:,1],c=y,edgecolor='k',cmap='cool')
plt.contourf(mx,my,df[:,:,i],100,cmap='hot',zorder=0)
plt.colorbar(pad=0.01)
plt.contour(mx,my,df[:,:,i],[0],cmap='hot',zorder=0.2)
plt.title(u'%d <> %d,%d,%d'%tuple([i]+list(set(range(4))-{i})),size=11)
plt.tight_layout()
plt.show()
จะเห็นว่าบริเวณที่มีค่ามากจนเป็นสีขาวๆในแต่ละภาพคือบริเวณที่ถูกแบ่งให้เป็นของกลุ่มนั้น รูปร่างที่ออกมาดูเหมือนมีจุดตัดมากมายนั่นที่จริงก็เกิดจากการแบ่งด้วยเส้นโค้งหลายเส้นตัดกัน
แต่นอกจากนี้ยังสามารถให้แสดงฟังก์ชันตัดสินใจของกลุ่มหนึ่งเทียบกับอีกกลุ่มหนึ่ง เทียบกันเป็นคู่ๆ
โดยไปปรับที่แอตทริบิวต์ decision_function_shape โดยให้ svc.decision_function_shape = 'ovo'
หรือจะกำหนดให้ชัดตั้งแต่ตอนสร้างออบเจ็กต์ก็ได้ คือเขียนเป็น scv = SVC(decision_function_shape='ovo')
เพียงแค่นี้ พอใช้ .decision_function() ผลที่ได้ก็จะเปลี่ยนไป กลายเป็นแบบที่เทียบกลุ่มหนึ่งกับอีกกลุ่มเป็นคู่ๆ
ซึ่งกรณีแบบนี้จะได้อาเรย์ขนาดเป็น (จำนวนจุดข้อมูล, m*(m-1)/2) โดย m คือจำนวนตัวแปร เช่น กรณีที่มีอยู่ ๔ ตัว ก็จะได้ออกมาเป็น ๖
ลองแสดงฟังก์ชันตัดสินใจทั้ง ๖ ออกมาดู
svc.decision_function_shape = 'ovo'
plt.figure(figsize=[7,7])
df = svc.decision_function(mX).reshape(200,200,-1)
k = [(i,j) for i in range(4) for j in range(4) if i<j]
for i in range(6):
plt.subplot(3,2,i+1,aspect=1,xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
s = np.maximum(y==k[i][0],y==k[i][1])
plt.scatter(X[s,0],X[s,1],c=y[s],edgecolor='k',cmap='cool',vmin=0,vmax=3)
vmax = np.abs(df[:,:,i]).max()
plt.contourf(mx,my,df[:,:,i],100,cmap='PuOr',zorder=0,vmin=-vmax,vmax=vmax)
plt.colorbar()
plt.contour(mx,my,df[:,:,i],[0],cmap='hot',zorder=0.1)
plt.title('%d<>%d'%k[i],size=11)
plt.tight_layout()
plt.show()
จะเห็นว่าโดยพื้นฐานแล้วภายใน SVC ได้สร้างตัวแบ่งแบบนี้ขึ้นมา ๖ อัน แล้วจึงนำไปแปลงผลเพื่อตัดสินว่าเขตไหนควรเป็นของกลุ่มไหนอีกที
ในทางกลับกันหากต้องการเปลี่ยนกลับเป็นแบบเปรียบเทียบกลุ่มหนึ่งกับกลุ่มที่เหลือก็ใส่ svc.decision_function_shape = 'ovr'
ข้อมูลเวกเตอร์ค้ำยันที่ได้
เมื่อทำการเรียนรู้จากข้อมูลที่ป้อนเข้าไปให้เสร็จ โปรแกรมจะบันทึกไว้ว่าจุดไหนที่ถูกใช้เป็นเวกเตอร์ค้ำยัน และจุดนั้นมีค่าตัวคูณลากรองจ์เป็นเท่าไหร่
.support_ คือ ดัชนีของตัวที่เป็นเวกเตอร์ค้ำยัน
.support_vectors_ คือ ค่าตำแหน่ง
.dual_coef_ คือ ตัวคูณลากรองจ์คูณกับคำตอบจริง (a*z)
dual_coef_ นั้นบ่งบอกถึงความสำคัญของเวกเตอร์ค้ำยันตัวนั้น ยิ่งห่างจากศูนย์มากก็ยิ่งมีผลต่อการคำนวณมาก
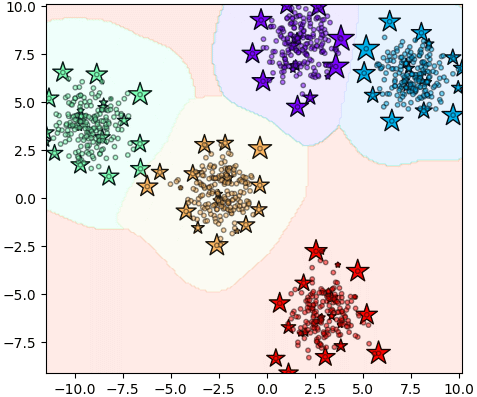
ลองใช้ SVC แบ่งกลุ่มเสร็จแล้วหาว่าเวกเตอร์ค้ำยันอยู่ตรงไหนบ้าง โดยแสดงเป็นรูปดาวที่มีขนาดแปรตามขนาดความสำคัญ
X,z = datasets.make_blobs(n_samples=1000,n_features=2,cluster_std=1,centers=5,random_state=20)
svc = SVC()
svc.fit(X,z)
print(svc.support_)
print(svc.support_vectors_)
print(svc.dual_coef_)
x_sv = svc.support_vectors_[:,0]
y_sv = svc.support_vectors_[:,1]
s_sv = np.abs(svc.dual_coef_)
s_sv = s_sv/s_sv.max()*400
c_sv = z[svc.support_]
plt.axes(aspect=1,xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.scatter(x_sv,y_sv,s=s_sv,c=c_sv,edgecolor='k',marker='*',cmap='rainbow')
plt.scatter(X[:,0],X[:,1],s=10,c=z,edgecolor='k',alpha=0.5,cmap='rainbow')
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),200),np.linspace(X[:,1].min(),X[:,1].max(),200))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = svc.predict(mX).reshape(200,200)
plt.contourf(mx,my,mz,alpha=0.1,cmap='rainbow')
plt.show()
จะเห็นว่าเวกเตอร์ค้ำยันมีอยู่จำนวนมากมายยืนอยู่ตามแถบรอบนอกของกลุ่ม
ทั้งหมดนี้เป็นตัวอย่างส่วนหนึ่งของการใช้ SVC ใน sklearn
นอกจากนี้แล้วก็ยังมีรายละเอียดปลีกย่อยและคำสั่งอีกหลายอย่างในนี้ที่ยังไม่ได้แนะนำอยู่ สามารถลองไปศึกษสและใช้กันต่อดูได้
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn