การบีบอัดข้อมูลรูปภาพด้วยการวิเคราะห์องค์ประกอบหลัก
เขียนเมื่อ 2019/09/28 19:37
แก้ไขล่าสุด 2021/09/28 16:42
การวิเคราะห์องค์ประกอบหลัก (主成分分析, principle component Analysis, PCA) นั้นใช้ประโยชน์ได้หลากหลายมาก
การบีบอัดข้อมูลก็เป็นเรื่องหนึ่งที่สามารถใช้การวิเคราะห์องค์ประกอบหลักทำได้
วิธีการแบบนี้บางทีก็เรียกว่า การแปลงกะร์ฮุเน็น-โลแอฟ (Karhunen–Loève transform)
การแปลงกะร์ฮุเน็น-โลแอฟนั้นจริงๆแล้วมีที่มาจากทฤษฎีบทกะร์ฮุเน็น-โลแอฟ (Karhunen–Loève theorem) หรือ ทฤษฎีบทโกสัมพี-กะร์ฮุเน็น-โลแอฟ (Kosambi–Karhunen–Loève theorem)
ชื่อนี้มาจากชื่อของ ๓ คน
- กะริ กะร์ฮุเน็น (Kari Karhunen) ชาวฟินแลนด์
- มีแชล โลแอฟ (Michel Loève) ชาวซีเรียเชื้อสายยิว แต่ใช้ชื่อภาษาฝรั่งเศส
- ทาโมทร ธรรมานันทะ โกสัมพี (Damodar Dharmananda Kosambi, दामोदर धर्मानन्द कोसाम्बी) ชาวอินเดีย
สำหรับบทนี้จะอธิบายการใช้การวิเคราะห์องค์ประกอบหลักเพื่อการบีดอัดข้อมูลรูปภาพ
ในส่วนของพื้นฐานเกี่ยวกับการวิเคราะห์องค์ประกอบหลักนั้นจะไม่อธิบายละเอียดในนี้ แต่มีเขียนไว้ใน https://phyblas.hinaboshi.com/20180727
วิธีการ
ปกติแล้วข้อมูลรูปภาพในคอมพิวเตอร์จะประกอบด้วยค่าสีของแต่ละจุดพิกเซล (pixel) โดยทั่วไปจำนวนข้อมูลที่ประกอบเป็นรูปภาพก็คือจำนวนพิกเซล
ข้อมูลภาพถือเป็นข้อมูลที่มีจำนวนมิติเท่ากับจำนวนจุดพิกเซล เช่น เช่นภาพขนาด ๖×๗ = ๔๒ พิกเซล ก็คือมี ๔๒ มิติ
ถ้าเป็นไฟล์ชนิด bmp จะบันทึกค่าสีของรูปภาพทั้งหมดจริงๆ ซึ่งจะเปลืองพื้นที่มาก โดยปกติจึงไฟล์ที่เก็บข้อมูลรูปภาพจึงมักจะมีการบีบอัดข้อมูล ไฟล์ไม่ได้มีขนาดใหญ่เท่าจำนวนพิกเซลจริงๆ
การวิเคราะห์องค์ประกอบหลักสามารถลดมิติของข้อมูลลง เมื่อลดมิติลงก็จะทำให้ประหยัดพื้นที่เก็บข้อมูล
สมมุติว่ามีภาพ n ภาพ แต่ละภาพมีจำนวนพิกเซล m (คือ กว้าง mx × สูง my) ก่อนอื่นต้องทำการแปลงให้แต่ละภาพกลายเป็นมิติเดียวก่อน เมื่อรวมทุกรูปเข้าด้วยกันก็ใส่ในอาเรย์ขนาด n แถว × m หลัก
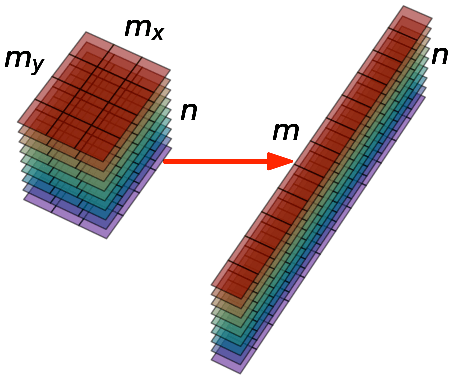
จากนั้นก็นำอาเรย์ที่ได้นี้มาทำการวิเคราะห์องค์ประกอบหลัก ลดจำนวนตัวแปรของข้อมูลลงจาก m มิติเหลือแค่จำนวนมิติเท่าที่ต้องการ
ต่อจากตรงนี้ขอยกตัวอย่างโดยใช้ข้อมูลตัวเลขของ MNIST ซึ่งใช้ sklearn โหลดมาได้ง่ายๆโดยตรง ส่วนการวิเคราะห์องค์ประกอบหลักก็ทำโดยใช้ sklearn
รายละเอียดและวิธีการใช้ข้อมูล MNIST นี้อ่านได้ใน https://phyblas.hinaboshi.com/20170920
ภาพตัวเลขของ MNIST เป็นภาพสีเดียวขนาด ๒๘×๒๘ = ๗๘๔ พิกเซล จึงมีจำนวนมิติข้อมูลเป็น ๗๘๔ มิติ
ข้อมูล MNIST มี ๗๐๐๐๐ ตัว แต่ในตัวอย่างนี้ขอดึงมาใช้ทดสอบแค่ ๑๐๐๐ ตัวเพื่อประหยัดเวลา จำนวนแค่นี้ก็เพียงพอ
ลองทำการวิเคราะห์องค์ประกอบหลัก เลือกเอา ๒๕ องค์ประกอบแรกมาเป็นองค์ประกอบหลัก จากนั้นลองเอาค่าน้ำหนักขององค์ประกอบมาวาดดู
จะได้ภาพซึ่งแสดงน้ำหนักของแต่ละองค์ประกอบที่มีต่อข้อมูลรูปภาพนี้ แต่ละภาพคือน้ำหนักของแต่ละองค์ประกอบ

ต่อมาลองดูค่าของข้อมูลตัวแรกที่แปลงมาอยู่ในพิกัดขององค์ประกอบทั้ง ๒๕ องค์ประกอบนี้ (เพื่อให้แสดงผลสะดวกจะแสดงในรูป กว้าง ๕ สูง ๕ แต่การเรียงแบบนี้ไม่ได้มีความหมายเป็นพิเศษ)
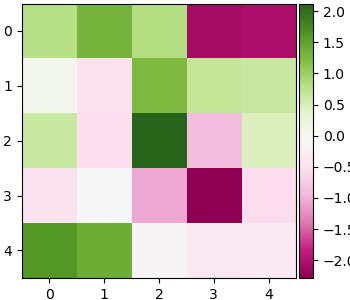
ในที่นี้เราแปลงข้อมูลจากข้อมูลเดิมซึ่งมี ๗๘๔ มิติ มาเป็นพิกัดขององค์ประกอบซึ่งมี ๒๕ มิติ ถ้าเก็บข้อมูลในรูปแบบนี้ได้จริงๆก็ประหยัดพื้นที่ไปได้ถึง ๓๐ เท่าเลยทีเดียว
ข้อมูล ๒๕ มิตินี้สามารถจะเอามาแปลงกลับเป็นข้อมูลเดิมได้โดย .inverse_transform() จะเป็นการเอาค่ามาคำนวณกับเมทริกซ์น้ำหนักแล้วรวมกันจนได้ภาพเดิม
ลองเอาข้อมูลนี้มาแปลงกลับแล้วเทียบกับภาพเดิมดู
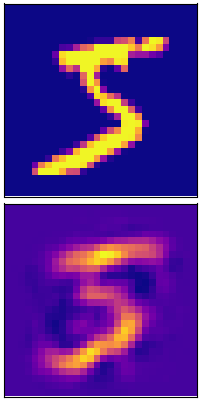
จะเห็นว่าได้เลข 5 คืนกลับมา แม้ว่าจะไม่ชัดเจน เพราะข้อมูลสูญเสียไปพอสมควรจากการบีบอัดจาก ๗๘๔ มิติเหลือ ๒๕ มิติ
การลดมิติข้อมูลจะทำให้สูญเสียรายละเอียดไปไม่มากก็น้อย ยิ่งลดมิติลงมากก็ยิ่งเสียไปมาก แลกมากับการที่ใช้พื้นที่ลดลง
ลองแสดงให้เห็นภาพชัดโดยการใส่องค์ประกอบเพิ่มไปเรื่อยๆทีละตัวแล้วเทียบรายละเอียดที่ได้
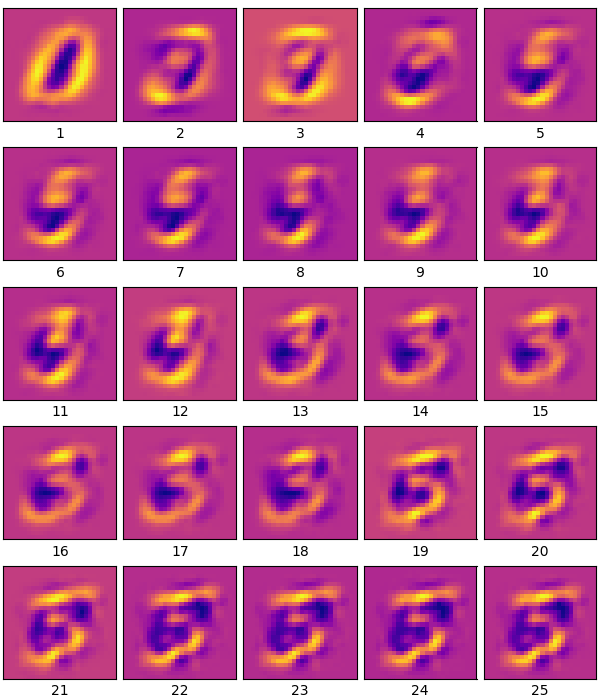
ภาพแรกจะมีองค์ประกอบเดียว ภาพต่อมาบวกเพิ่มองค์ประกอบที่ ๒ เข้าไป ยิ่งภาพต่อๆไปยิ่งบวกเพิ่มขึ้นเรื่อยๆ จนภาพสุดท้ายครบ ๒๕ ค่อยๆเห็นเป็นรูปเป็นร่างมากขึ้นเรื่อยๆตามลำดับ
ข้อมูลที่สูญหายไปกับมิติ
ลองพิจารณาค่าอัตราความบ่งบอกความแปรปรวน ซึ่งเก็บอยู่ในแอตทริบิวต์ .explained_variance_ratio_
ค่านี้จะเป็นตัวบอกว่าองค์ประกอบไหนมีผลต่อการคืนสู่ค่าเดิมแค่ไหน องค์ประกอบตัวแรกจะมีค่ามากที่สุด และยิ่งตัวหลังๆจะน้อยจนแทบเป็น 0 ดังนั้นตัดทิ้งไปก็แทบไม่มีผล
ผลรวมระหว่างค่าอัตราความบ่งบอกความแปรปรวนขององค์ประกอบทั้งหมดที่เลือก แล้วเอามาลบออกจาก 1 ก็จะได้เป็นอัตราของข้อมูลที่สูญเสียไป
ลองดูว่าใช้กี่มิติแล้วจะเหลือข้อมูลแค่ไหน
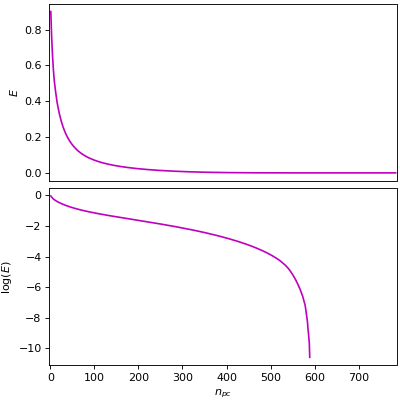
ข้อมูลเดิมมีทั้งหมด ๗๘๔ พิกเซล จึงแยกออกได้เป็น ๗๘๔ องค์ประกอบ
จะเห็นว่าองค์ประกอบสักแค่ ๕๐๐ ตัวแรกก็แทบจะอธิบายข้อมูลได้ทั้งหมดแล้ว ยิ่งตัวหลังๆยิ่งไม่มีความสำคัญตัดทิ้งได้
ลองสร้างภาพตัวเลขแต่ละตัวแล้วเอามาเทียบดูว่าใช้องค์ประกอบกี่ตัวจะคืนภาพมาได้ชัดแค่ไหน
1 องค์ประกอบ แทบไม่เห็นเค้า

4 พอจะเริ่มเห็นเค้าแต่ยังอ่านยาก

25 ชัดพอที่จะเริ่มอ่านได้

100 ค่อนข้างชัดแล้ว แต่ยังเห็นความเบลอเล็กๆน้อยๆ

400 แทบจะเหมือนภาพเดิมแล้ว แต่จริงๆยังมีความต่างอยู่เล็กน้อยในระดับที่ตาเปล่าแยกไม่ออก
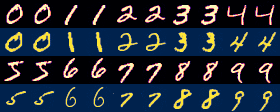
784 องค์ประกอบทั้งหมดใช้ครบ แน่นอนว่ากลับมาเป็นเหมือนภาพเดิม
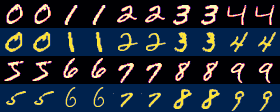
ข้อมูลที่ใช้เรียนรู้ (ข้อมูลฝึก) กับข้อมูลที่ไม่ได้ใช้เรียนรู้ (ข้อมูลทดสอบ)
วิธีการนี้จะได้ผลดีแค่ไหนก็ขึ้นอยู่กับตัวอย่างที่เอามาใช้เป็นข้อมูลในการเรียนรู้
ข้อมูลจำนวนน้อยๆมีแนวโน้มที่จะให้ประสิทธิภาพดีเมื่อใช้กับข้อมูลที่อยู่ในกลุ่มที่ใช้เรียนรู้ แต่ถ้าลองใช้กับข้อมูลที่ไม่ได้เรียนรู้ก็จะได้ผลแย่ลง
ยิ่งใช้ข้อมูลในการเรียนรู้มากก็ยิ่งสามารถคืนค่าข้อมูลที่ไม่ได้เรียนรู้ได้ใกล้เคียงมากขึ้น
ลองทดสอบด้วยข้อมูลตัวเลขชุดเดิม แต่ให้เรียนรู้ด้วยจำนวนต่างๆกัน แล้วให้ลองใช้กับภาพที่ไม่ได้อยู่ในข้อมูลกลุ่มฝึก ดูว่าจะทำให้ภาพกลับคืนมาได้ใกล้เคียงเดิมแค่ไหน
ผลที่ได้
64 ภาพ

225 ภาพ

784 ภาพ

2025 ภาพ

16000 ภาพ

จะเห็นว่ายิ่งมีข้อมูลมากก็ยิ่งทำให้ได้ภาพใกล้เคียงเดิมมากขึ้น
ต่อมาลองมาทดสอบดูโดยสร้างข้อมูลสุ่มขึ้นมา ๒ ชุด เป็นข้อมูล ๑๐๐ มิติ จากนั้นการใช้วิเคราะห์องค์ประกอบหลักเอาองค์ประกอบแค่ ๔ ตัว แล้วลองแปลงข้อมูลไปแล้วแปลงกลับแล้วเทียบดูว่าต่างจากเดิมแค่ไหนโดยคำนวณผลรวมของผลต่างกำลังสอง ข้อมูลเทียบระหว่างข้อมูลที่อยู่ในกลุ่มที่ใช้ฝึกและข้อมูลที่ไม่ได้อยู่ในกลุ่มที่เรียนรู้
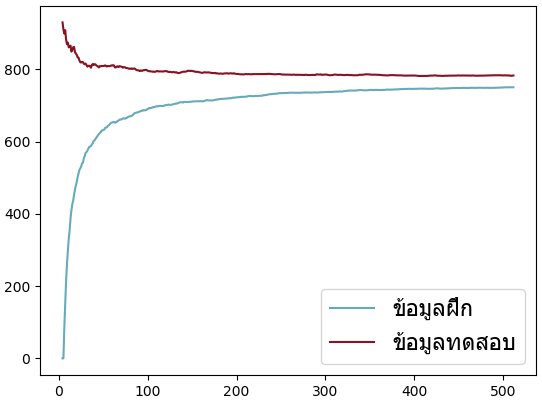
จากผลที่ได้จะเห็นว่าเมื่อใช้ข้อมูลน้อยๆความแตกต่างระหว่างข้อมูลที่ใช้ฝึกกับที่ใช้ทดสอบจะมากอย่างเห็นได้ชัด ยิ่งเรียนรู้ไปมากความแตกต่างนั้นก็ยิ่งเข้าใกล้กัน
แต่สำหรับข้อมูลที่ไม่ได้อยู่ในขอบเขตกลุ่มใกล้เคียงกับที่ฝึกเลย ไม่ว่าจะเรียนรู้ด้วยข้อมูลมากแค่ไหนก็ไม่มีประโยชน์ เพราะข้อมูลจะใช้งานได้ดีกับข้อมูลที่อยู่ในข่ายเดียวกันกับที่ใช้ฝึกเท่านั้น
ตัวอย่างเช่น ข้อมูลฝึกเป็นเลข 0 ถึง 99 แต่กลับใช้ข้อมูลที่เป็นเลข 100 ถึง 199 มาทดสอบ แบบนี้
ดังนั้นถ้าจะบีบอัดข้อมูลด้วยวิธีนี้ก็ควรรู้ว่าข้อมูลที่มีอยู่นั้นเป็นข้อมูลประเภทไหนมีค่าอยู่ในขอบเขตไหน
สิ่งที่สำคัญสำหรับข้อมูลที่ใช้ในการเรียนรู้ก็คือ ความครอบคลุม เพื่อให้ข้อมูลที่ใช้เรียนรู้สามารถเป็นตัวแทนของข้อมูลทั่วๆไปได้
อ้างอิง
การบีบอัดข้อมูลก็เป็นเรื่องหนึ่งที่สามารถใช้การวิเคราะห์องค์ประกอบหลักทำได้
วิธีการแบบนี้บางทีก็เรียกว่า การแปลงกะร์ฮุเน็น-โลแอฟ (Karhunen–Loève transform)
การแปลงกะร์ฮุเน็น-โลแอฟนั้นจริงๆแล้วมีที่มาจากทฤษฎีบทกะร์ฮุเน็น-โลแอฟ (Karhunen–Loève theorem) หรือ ทฤษฎีบทโกสัมพี-กะร์ฮุเน็น-โลแอฟ (Kosambi–Karhunen–Loève theorem)
ชื่อนี้มาจากชื่อของ ๓ คน
- กะริ กะร์ฮุเน็น (Kari Karhunen) ชาวฟินแลนด์
- มีแชล โลแอฟ (Michel Loève) ชาวซีเรียเชื้อสายยิว แต่ใช้ชื่อภาษาฝรั่งเศส
- ทาโมทร ธรรมานันทะ โกสัมพี (Damodar Dharmananda Kosambi, दामोदर धर्मानन्द कोसाम्बी) ชาวอินเดีย
สำหรับบทนี้จะอธิบายการใช้การวิเคราะห์องค์ประกอบหลักเพื่อการบีดอัดข้อมูลรูปภาพ
ในส่วนของพื้นฐานเกี่ยวกับการวิเคราะห์องค์ประกอบหลักนั้นจะไม่อธิบายละเอียดในนี้ แต่มีเขียนไว้ใน https://phyblas.hinaboshi.com/20180727
วิธีการ
ปกติแล้วข้อมูลรูปภาพในคอมพิวเตอร์จะประกอบด้วยค่าสีของแต่ละจุดพิกเซล (pixel) โดยทั่วไปจำนวนข้อมูลที่ประกอบเป็นรูปภาพก็คือจำนวนพิกเซล
ข้อมูลภาพถือเป็นข้อมูลที่มีจำนวนมิติเท่ากับจำนวนจุดพิกเซล เช่น เช่นภาพขนาด ๖×๗ = ๔๒ พิกเซล ก็คือมี ๔๒ มิติ
ถ้าเป็นไฟล์ชนิด bmp จะบันทึกค่าสีของรูปภาพทั้งหมดจริงๆ ซึ่งจะเปลืองพื้นที่มาก โดยปกติจึงไฟล์ที่เก็บข้อมูลรูปภาพจึงมักจะมีการบีบอัดข้อมูล ไฟล์ไม่ได้มีขนาดใหญ่เท่าจำนวนพิกเซลจริงๆ
การวิเคราะห์องค์ประกอบหลักสามารถลดมิติของข้อมูลลง เมื่อลดมิติลงก็จะทำให้ประหยัดพื้นที่เก็บข้อมูล
สมมุติว่ามีภาพ n ภาพ แต่ละภาพมีจำนวนพิกเซล m (คือ กว้าง mx × สูง my) ก่อนอื่นต้องทำการแปลงให้แต่ละภาพกลายเป็นมิติเดียวก่อน เมื่อรวมทุกรูปเข้าด้วยกันก็ใส่ในอาเรย์ขนาด n แถว × m หลัก

จากนั้นก็นำอาเรย์ที่ได้นี้มาทำการวิเคราะห์องค์ประกอบหลัก ลดจำนวนตัวแปรของข้อมูลลงจาก m มิติเหลือแค่จำนวนมิติเท่าที่ต้องการ
ต่อจากตรงนี้ขอยกตัวอย่างโดยใช้ข้อมูลตัวเลขของ MNIST ซึ่งใช้ sklearn โหลดมาได้ง่ายๆโดยตรง ส่วนการวิเคราะห์องค์ประกอบหลักก็ทำโดยใช้ sklearn
รายละเอียดและวิธีการใช้ข้อมูล MNIST นี้อ่านได้ใน https://phyblas.hinaboshi.com/20170920
ภาพตัวเลขของ MNIST เป็นภาพสีเดียวขนาด ๒๘×๒๘ = ๗๘๔ พิกเซล จึงมีจำนวนมิติข้อมูลเป็น ๗๘๔ มิติ
ข้อมูล MNIST มี ๗๐๐๐๐ ตัว แต่ในตัวอย่างนี้ขอดึงมาใช้ทดสอบแค่ ๑๐๐๐ ตัวเพื่อประหยัดเวลา จำนวนแค่นี้ก็เพียงพอ
ลองทำการวิเคราะห์องค์ประกอบหลัก เลือกเอา ๒๕ องค์ประกอบแรกมาเป็นองค์ประกอบหลัก จากนั้นลองเอาค่าน้ำหนักขององค์ประกอบมาวาดดู
from sklearn.decomposition import PCA
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
mnist = datasets.fetch_openml('mnist_784') # อ่านข้อมูล
X = mnist.data[:1000]/255 # เอาแค่ 1000 ตัว
z = mnist.target[:1000].astype(int)
pca = PCA(25) # ออบเจ็กต์วิเคราะห์องค์ประกอบหลัก จำนวนองค์ประกอบหลักเป็น 25
pca.fit(X) # เริ่มเรียนรู้
# ได้ค่าน้ำหนักของแต่ละองค์ประกอบมา เอามาลองแสดงผลดู
compo = pca.components_.reshape(25,28,28)
plt.figure(figsize=[6,6])
for i in range(25):
plt.subplot(5,5,1+i,xticks=[],yticks=[])
plt.imshow(compo[i],cmap='plasma')
plt.axis('off')
plt.tight_layout(1)
plt.show()จะได้ภาพซึ่งแสดงน้ำหนักของแต่ละองค์ประกอบที่มีต่อข้อมูลรูปภาพนี้ แต่ละภาพคือน้ำหนักของแต่ละองค์ประกอบ

ต่อมาลองดูค่าของข้อมูลตัวแรกที่แปลงมาอยู่ในพิกัดขององค์ประกอบทั้ง ๒๕ องค์ประกอบนี้ (เพื่อให้แสดงผลสะดวกจะแสดงในรูป กว้าง ๕ สูง ๕ แต่การเรียงแบบนี้ไม่ได้มีความหมายเป็นพิเศษ)
Xi = pca.transform(X)
plt.figure(figsize=[3.5,3])
plt.imshow(Xi[0].reshape(5,5),cmap='PiYG')
plt.colorbar(pad=0.01)
plt.tight_layout(0)
plt.show()
ในที่นี้เราแปลงข้อมูลจากข้อมูลเดิมซึ่งมี ๗๘๔ มิติ มาเป็นพิกัดขององค์ประกอบซึ่งมี ๒๕ มิติ ถ้าเก็บข้อมูลในรูปแบบนี้ได้จริงๆก็ประหยัดพื้นที่ไปได้ถึง ๓๐ เท่าเลยทีเดียว
ข้อมูล ๒๕ มิตินี้สามารถจะเอามาแปลงกลับเป็นข้อมูลเดิมได้โดย .inverse_transform() จะเป็นการเอาค่ามาคำนวณกับเมทริกซ์น้ำหนักแล้วรวมกันจนได้ภาพเดิม
ลองเอาข้อมูลนี้มาแปลงกลับแล้วเทียบกับภาพเดิมดู
plt.figure(figsize=[2,4])
# ภาพเดิม
plt.subplot(211,xticks=[],yticks=[])
plt.imshow(X[0].reshape(28,28),cmap='plasma')
# ภาพหลังแปลงกลับด้วยองค์ประกอบหลัก ๒๕ ตัว
plt.subplot(212,xticks=[],yticks=[])
plt.imshow(pca.inverse_transform(Xi[0]).reshape(28,28),cmap='plasma')
plt.tight_layout(0)
plt.show()
จะเห็นว่าได้เลข 5 คืนกลับมา แม้ว่าจะไม่ชัดเจน เพราะข้อมูลสูญเสียไปพอสมควรจากการบีบอัดจาก ๗๘๔ มิติเหลือ ๒๕ มิติ
การลดมิติข้อมูลจะทำให้สูญเสียรายละเอียดไปไม่มากก็น้อย ยิ่งลดมิติลงมากก็ยิ่งเสียไปมาก แลกมากับการที่ใช้พื้นที่ลดลง
ลองแสดงให้เห็นภาพชัดโดยการใส่องค์ประกอบเพิ่มไปเรื่อยๆทีละตัวแล้วเทียบรายละเอียดที่ได้
plt.figure(figsize=[6,7])
for n_pc in range(1,26):
plt.subplot(5,5,n_pc,xticks=[],yticks=[],xlabel=n_pc)
X2 = (Xi[0,:n_pc].dot(pca.components_[:n_pc])).reshape(28,28)
plt.imshow(X2,cmap='plasma')
plt.tight_layout(0)
plt.show()
ภาพแรกจะมีองค์ประกอบเดียว ภาพต่อมาบวกเพิ่มองค์ประกอบที่ ๒ เข้าไป ยิ่งภาพต่อๆไปยิ่งบวกเพิ่มขึ้นเรื่อยๆ จนภาพสุดท้ายครบ ๒๕ ค่อยๆเห็นเป็นรูปเป็นร่างมากขึ้นเรื่อยๆตามลำดับ
ข้อมูลที่สูญหายไปกับมิติ
ลองพิจารณาค่าอัตราความบ่งบอกความแปรปรวน ซึ่งเก็บอยู่ในแอตทริบิวต์ .explained_variance_ratio_
ค่านี้จะเป็นตัวบอกว่าองค์ประกอบไหนมีผลต่อการคืนสู่ค่าเดิมแค่ไหน องค์ประกอบตัวแรกจะมีค่ามากที่สุด และยิ่งตัวหลังๆจะน้อยจนแทบเป็น 0 ดังนั้นตัดทิ้งไปก็แทบไม่มีผล
ผลรวมระหว่างค่าอัตราความบ่งบอกความแปรปรวนขององค์ประกอบทั้งหมดที่เลือก แล้วเอามาลบออกจาก 1 ก็จะได้เป็นอัตราของข้อมูลที่สูญเสียไป
ลองดูว่าใช้กี่มิติแล้วจะเหลือข้อมูลแค่ไหน
mnist = datasets.fetch_openml('mnist_784')
X = mnist.data[:1000]/255
z = mnist.target[:1000].astype(int)
pca = PCA(784)
pca.fit(X)
E = 1-pca.explained_variance_ratio_.cumsum()
plt.figure(figsize=[5,5],dpi=80)
# สเกลธรรมดา
plt.subplot(211,ylabel='$E$',xlim=[-2,786],xticks=[])
plt.plot(range(1,785),E,'m')
# สเกลลอการิธึม
plt.subplot(212,ylabel='$\log(E)$',xlim=[-2,786],xlabel='$n_{pc}$')
plt.plot(range(1,785),np.log10(E),'m')
plt.tight_layout(0)
plt.show()
ข้อมูลเดิมมีทั้งหมด ๗๘๔ พิกเซล จึงแยกออกได้เป็น ๗๘๔ องค์ประกอบ
จะเห็นว่าองค์ประกอบสักแค่ ๕๐๐ ตัวแรกก็แทบจะอธิบายข้อมูลได้ทั้งหมดแล้ว ยิ่งตัวหลังๆยิ่งไม่มีความสำคัญตัดทิ้งได้
ลองสร้างภาพตัวเลขแต่ละตัวแล้วเอามาเทียบดูว่าใช้องค์ประกอบกี่ตัวจะคืนภาพมาได้ชัดแค่ไหน
lis_n_pc = [784,400,100,25,4,1] # จำนวนองค์ประกอบหลัก
pca = PCA(784)
pca.fit(X)
for n_pc in lis_n_pc:
pca.components_ = pca.components_[:n_pc] # เอาจำนวนองค์ประกอบหลักเหลือตามจำนวนที่กำหนดแต่ละรอบ
X2 = pca.inverse_transform(pca.transform(X)) # แปลงไปแล้วแปลงกลับทันที
XXX = []
for lek in range(0,10):
i1,i2 = np.where(z==lek)[0][:2]
X11 = X.reshape(-1,28,28)[i1] # ภาพเดิม ภาพที่ ๑
X12 = X.reshape(-1,28,28)[i2] # ภาพเดิม ภาพที่ ๒
X21 = X2.reshape(-1,28,28)[i1] # ภาพหลังแปลงกลับ ภาพที่ ๑
X22 = X2.reshape(-1,28,28)[i2] # ภาพหลังแปลงกลับ ภาพที่ ๒
XXX.append(np.vstack([plt.get_cmap('magma')(np.hstack([X11,X21])),plt.get_cmap('cividis')(np.hstack([X12,X22]))]))
XXX = np.hstack(np.hstack(np.array(XXX).reshape(2,5,*XXX[0].shape)))
plt.imsave('kl%03d.png'%(n_pc),XXX)
plt.close()
print('%d: %f'%(n_pc,pca.explained_variance_ratio_[:n_pc].sum()))1 องค์ประกอบ แทบไม่เห็นเค้า

4 พอจะเริ่มเห็นเค้าแต่ยังอ่านยาก

25 ชัดพอที่จะเริ่มอ่านได้

100 ค่อนข้างชัดแล้ว แต่ยังเห็นความเบลอเล็กๆน้อยๆ

400 แทบจะเหมือนภาพเดิมแล้ว แต่จริงๆยังมีความต่างอยู่เล็กน้อยในระดับที่ตาเปล่าแยกไม่ออก
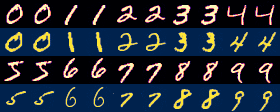
784 องค์ประกอบทั้งหมดใช้ครบ แน่นอนว่ากลับมาเป็นเหมือนภาพเดิม
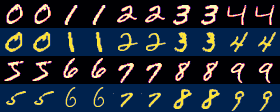
ข้อมูลที่ใช้เรียนรู้ (ข้อมูลฝึก) กับข้อมูลที่ไม่ได้ใช้เรียนรู้ (ข้อมูลทดสอบ)
วิธีการนี้จะได้ผลดีแค่ไหนก็ขึ้นอยู่กับตัวอย่างที่เอามาใช้เป็นข้อมูลในการเรียนรู้
ข้อมูลจำนวนน้อยๆมีแนวโน้มที่จะให้ประสิทธิภาพดีเมื่อใช้กับข้อมูลที่อยู่ในกลุ่มที่ใช้เรียนรู้ แต่ถ้าลองใช้กับข้อมูลที่ไม่ได้เรียนรู้ก็จะได้ผลแย่ลง
ยิ่งใช้ข้อมูลในการเรียนรู้มากก็ยิ่งสามารถคืนค่าข้อมูลที่ไม่ได้เรียนรู้ได้ใกล้เคียงมากขึ้น
ลองทดสอบด้วยข้อมูลตัวเลขชุดเดิม แต่ให้เรียนรู้ด้วยจำนวนต่างๆกัน แล้วให้ลองใช้กับภาพที่ไม่ได้อยู่ในข้อมูลกลุ่มฝึก ดูว่าจะทำให้ภาพกลับคืนมาได้ใกล้เคียงเดิมแค่ไหน
nnn = [64,225,784,2025,16000] # จำนวนข้อมูลที่ใช้
for n in nnn:
# ข้อมูลที่ใช้ฝึก
X = mnist.data[:n]/255
z = mnist.target[:n].astype(int)
pca = PCA(64)
pca.fit(X)
# ข้อมูลทดสอบ ใช้ส่วนที่ไม่ซ้ำกับข้อมูลที่ใช้ฝึกเรียนรู้
X = mnist.data[16000:16100]/255
z = mnist.target[16000:16100].astype(int)
# แปลงข้อมูลไปแล้วแปลงกลับทันที
X2 = pca.inverse_transform(pca.transform(X))
XXX = []
for lek in range(0,10):
i1,i2 = np.where(z==lek)[0][:2]
X11 = X.reshape(-1,28,28)[i1] # ภาพเดิม ภาพที่ ๑
X12 = X.reshape(-1,28,28)[i2] # ภาพเดิม ภาพที่ ๒
X21 = X2.reshape(-1,28,28)[i1] # ภาพหลังแปลงกลับ ภาพที่ ๑
X22 = X2.reshape(-1,28,28)[i2] # ภาพหลังแปลงกลับ ภาพที่ ๒
XXX.append(np.vstack([plt.get_cmap('magma')(np.hstack([X11,X21])),plt.get_cmap('cividis')(np.hstack([X12,X22]))]))
XXX = np.hstack(np.hstack(np.array(XXX).reshape(2,5,*XXX[0].shape)))
plt.imsave('kln%05d.png'%n,XXX)
plt.close()ผลที่ได้
64 ภาพ

225 ภาพ

784 ภาพ

2025 ภาพ

16000 ภาพ

จะเห็นว่ายิ่งมีข้อมูลมากก็ยิ่งทำให้ได้ภาพใกล้เคียงเดิมมากขึ้น
ต่อมาลองมาทดสอบดูโดยสร้างข้อมูลสุ่มขึ้นมา ๒ ชุด เป็นข้อมูล ๑๐๐ มิติ จากนั้นการใช้วิเคราะห์องค์ประกอบหลักเอาองค์ประกอบแค่ ๔ ตัว แล้วลองแปลงข้อมูลไปแล้วแปลงกลับแล้วเทียบดูว่าต่างจากเดิมแค่ไหนโดยคำนวณผลรวมของผลต่างกำลังสอง ข้อมูลเทียบระหว่างข้อมูลที่อยู่ในกลุ่มที่ใช้ฝึกและข้อมูลที่ไม่ได้อยู่ในกลุ่มที่เรียนรู้
m = 100 # จำนวนมิติข้อมูลเดิม
n = 512 # จำนวนข้อมูล
k = 4 # จำนวนองค์ประกอบหลัก
X1 = np.random.randint(0,99,[n,m]) # ชุดข้อมูลฝึก
X2 = np.random.randint(0,99,[n,m]) # ชุดข้อมูลทดสอบ สุ่มค่าในช่วงเดียวกัน
v = [[],[]]
nn = range(k,n+1)
for i in nn:
pca = PCA(k)
pca.fit(X1[:i])
v[0].append(((X1[:i]-pca.inverse_transform(pca.transform(X1[:i])))**2).mean())
v[1].append(((X2[:i]-pca.inverse_transform(pca.transform(X2[:i])))**2).mean())
plt.plot(nn,v[0],'#66AABB',label='ข้อมูลฝึก')
plt.plot(nn,v[1],'#881122',label='ข้อมูลทดสอบ')
plt.legend(prop={'family':'Tahoma', 'size':16})
plt.show()
จากผลที่ได้จะเห็นว่าเมื่อใช้ข้อมูลน้อยๆความแตกต่างระหว่างข้อมูลที่ใช้ฝึกกับที่ใช้ทดสอบจะมากอย่างเห็นได้ชัด ยิ่งเรียนรู้ไปมากความแตกต่างนั้นก็ยิ่งเข้าใกล้กัน
แต่สำหรับข้อมูลที่ไม่ได้อยู่ในขอบเขตกลุ่มใกล้เคียงกับที่ฝึกเลย ไม่ว่าจะเรียนรู้ด้วยข้อมูลมากแค่ไหนก็ไม่มีประโยชน์ เพราะข้อมูลจะใช้งานได้ดีกับข้อมูลที่อยู่ในข่ายเดียวกันกับที่ใช้ฝึกเท่านั้น
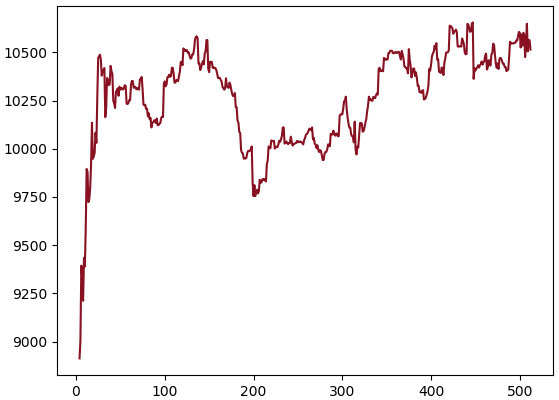
ตัวอย่างเช่น ข้อมูลฝึกเป็นเลข 0 ถึง 99 แต่กลับใช้ข้อมูลที่เป็นเลข 100 ถึง 199 มาทดสอบ แบบนี้
X1 = np.random.randint(0,100,[n,m]) # ชุดข้อมูลฝึก
X3 = X1+100 # ชุดข้อมูลทดสอบ บวกค่าเพิ่มไปให้ค่าอยู่ในช่วงต่างจากชุดข้อมูลฝึก
v = []
for i in nn:
pca = PCA(k)
pca.fit(X1[:i])
v.append(((X3[:i]-pca.inverse_transform(pca.transform(X3[:i])))**2).mean())
plt.plot(nn,v,'#881122')
plt.show()
ดังนั้นถ้าจะบีบอัดข้อมูลด้วยวิธีนี้ก็ควรรู้ว่าข้อมูลที่มีอยู่นั้นเป็นข้อมูลประเภทไหนมีค่าอยู่ในขอบเขตไหน
สิ่งที่สำคัญสำหรับข้อมูลที่ใช้ในการเรียนรู้ก็คือ ความครอบคลุม เพื่อให้ข้อมูลที่ใช้เรียนรู้สามารถเป็นตัวแทนของข้อมูลทั่วๆไปได้
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy