ต่อจาก บทที่ ๑๕

ในบทนี้จะเป็นเรื่องของการแจกแจงแกมมา ซึ่งใช้เป็นการแจกแจงความน่าจะเป็นของค่าพารามิเตอร์ของการแจกแจงอื่นๆหลายชนิด

การแจกแจงแกมมา

การแจกแจงแกมมา (γ分布, gamma distribution) เป็นการแจกแจงที่อาจใช้เป็นความน่าจะเป็นก่อนหน้าสังยุคของการแจกแจงแบบปกติ, การแจกแจงปัวซง และ การแจกแจงแบบเลขชี้กำลัง

ก่อนอื่นขอเริ่มจากแนะนำรูปทั่วไปของการแจกแจงแกมมา

ฟังก์ชันการแจกแจงความหนาแน่นความน่าจะเป็นของการแจกแจงแกมมาเป็นดังนี้


พารามิเตอร์มีอยู่ 2 ตัวคือ ν กับ β ซึ่งค่าอาจเป็นจำนวนจริงบวกใดๆ

ในบางครั้งอาจเขียนในรูปแบบนี้แทน


โดย θ=1/β เป็นส่วนกลับของ β

จะเขียนแบบไหนแล้วแต่ว่าจะใช้ในสมการไหน สำหรับกรณีที่กำลังจะใช้ต่อไปนี้จะเขียนในรูป β เนื่องจากสะดวกในการคำนวณมากกว่า

นอกจากนี้อักษรที่ใช้เป็นตัวแปรก็ต่างกันไปมากขึ้นอยู่กับว่าตำราไหน ที่จริงตัวแปรที่เขียนเป็น ν ในที่นี้มักถูกเขียนด้วย α หรือ λ มากกว่า แต่ทั้งสองตัวนี้ถูกใช้เป็นตัวแปรอย่างอื่นไปแล้วจึงขอใช้ ν (นิว)

ส่วน Γ คือฟังก์ชันแกมมา ซึ่งในกรณีทั่วไปคำนวณได้จาก


ถ้า ν มีค่าเป็นจำนวนเต็ม ก็จะเท่ากับแฟกทอเรียลลบหนึ่ง ซึ่งสามารถคำนวณได้ง่ายเป็น


หรือกรณีที่เป็นจำนวนเต็มบวกด้วย 1/2 จะคำนวณได้เป็น


กรณีที่ใช้กับพารามิเตอร์ของการแจกแจงแบบเลขชี้กำลังหรือการแจกแจงปัวซง ปกติแล้ว ν มักจะเป็นจำนวนเต็ม และเมื่อใช้กับการแจกแจงแบบปกติมักเป็นจำนวนเต็มหรือมีเศษ 1/2

กราฟแสดงตัวอย่างค่าความหนาแน่นของความน่าจะเป็นของการแจกแจงแกมมาในกรณีต่างๆ



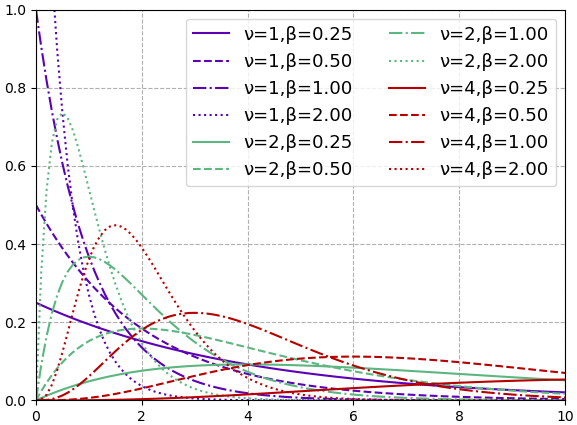
ค่าคาดหมายของการแจกแจงแกมมาจะอยู่ที่


ค่าสูงสุดของการแจกแจงแกมมาจะอยู่ที่


เพียงแต่ถ้า ν<1 จะไม่มีจุดสูงสุด

ความแปรปรวนเท่ากับ


ในที่นี้จะใช้ $\mathcal{Gã}$ แทนการแจกแจงแกมมาโดยเขียนแบบนี้





การแจกแจงความน่าจะเป็นของพารามิเตอร์ความเที่ยงตรงในการแจกแจงแบบปกติ

ต่อไปเริ่มยกตัวอย่างการใช้การแจกแจงแกมมา โดยเริ่มจากใช้เป็นความน่าจะเป็นก่อนหน้าสังยุคของการแจกแจงแบบปกติ

รูปทั่วไปของการแจกแจงแบบปกติคือ


ในบทที่ ๑๕ ได้เขียนถึงการแจกแจงพารามิเตอร์ μ โดยถือว่า σ เป็นค่าที่รู้อยู่แน่นอนแล้ว ส่วนในบทนี้จะทำในกรณีตรงกันข้ามกัน คือมีค่า μ อยู่ตายตัวแล้วต้องการหา σ

เพียงแต่เพื่อความสะดวก แทนที่จะพิจารณาการแจกแจงของส่วนเบี่ยงเบนมาตรฐาน σ หรือความแปรปรวน σ² โดยทั่วไปมักจะคำนวณในรูปของส่วนกลับของความแปรปรวน เรียกว่า พารามิเตอร์ความเที่ยงตรง (精度参数, precision parameter)


ที่จริงถ้าจะหาการแจกแจงในรูปของความแปรปรวน σ² ก็ทำได้ แต่จะกลายเป็นการแจกแจงแกมมาผกผัน (逆γ分布, inverse gamma distribution) ซึ่งก็คล้ายการแจกแจงแกมมาแต่ไม่นิยมใช้มากเท่า ในที่นี้ก็จะใช้ α เพื่อจะได้เป็นการแจกแจงแกมมาธรรมดา

เมื่อแทนด้วย α การแจกแจงแบบปกติจะเขียนใหม่ได้เป็นดังนี้


ปกติเมื่อเขียนแทนด้วย $\mathcal{N}$ ค่าตัวขวาสุดจะเขียนเป็นความแปรปรวน σ² ในที่นี้แม้จะเขียนในรูปของ α ก็ให้เขียนเป็นส่วนกลับ α^-1 ซึ่งเท่ากับ σ²

ในที่นี้จะพิจารณาค่าพารามิเตอร์ α โดยใช้ทฤษฎีบทของเบส์ เช่นเดียวกับที่ทำกับ μ ในบทที่แล้ว แต่ครั้งนี้ตัวแปรที่พิจารณาคือ α

เมื่อมีข้อมูล x₁ ที่เกิดจากการสุ่มโดยมีการแจกแจงความน่าจะเป็นแบบปกติ สามารถหา α ตามทฤษฎีบทของเบส์ได้โดย


ความน่าจะเป็นก่อนหน้าเมื่อไม่มีข้อมูลอะไรอาจให้เป็นค่าคงตัวไป ซึ่งการแจกแจงแบบค่าคงตัวก็ถือเป็นฟังก์ชันแกมมารูปแบบหนึ่ง คือในกรณีที่ ν=1 และ β เป็นค่าเล็กๆเข้าใกล้ 0


ส่วนฟังก์ชันควรจะเป็นคือ


เมื่อแทนลงไปแล้วก็จะคำนวณการแจกแจงความน่าจะเป็นภายหลังได้เป็น


เมื่อพิจารณาค่า α จะพบว่า α สามารถเขียนในรูปการแจกแจงแกมมาเป็น


ก็จะได้ว่า


และถ้าหากมีข้อมูล x₂ ที่เป็นผลจากการแจกเดิมเพิ่มเข้ามาอีกก็จะได้ว่า


และเมื่อมีข้อมูลเข้ามาทั้งหมด n ตัวก็จะได้ว่า


จะเห็นว่าเมื่อมีข้อมูลใส่เข้ามา ค่า α จะบวกเพิ่มไปตัวละ 1/2 ส่วน β จะเป็นครึ่งหนึ่งของผลรวมของระยะห่างกำลังสองจาก μ

ในกรณีที่ความน่าจะเป็นตั้งต้นมีค่าอยู่แล้วเป็นฟังก์ชันแกมมาที่มีพารามิเตอร์เริ่มต้นเป็น ν=ν₀, β=β₀


การแจกแจงความน่าจะเป็นภายหลังก็จะได้เป็น


ต่อไปเป็นโค้ดตัวอย่าง โดยจะสร้างข้อมูลที่สุ่มโดยแจกแจงแบบปกติ โดยที่รู้ค่า μ จริงอยู่แล้วแต่ไม่รู้ σ แล้วพยายามหาค่า σ จากการแจกแจงนี้ ดูลักษณะการแจกแจงและจุดสูงสุดที่ได้เมื่อเพิ่มข้อมูลเข้ามาเรื่อยๆ

import random

ν0 = 1 # ν เริ่มต้น
β0 = 0.01 # β เริ่มต้น
μ = 8 # μ จริงๆของการแจกแจง
σ = 2 # σ จริงๆของการแจกแจง
α = 1/σ**2 # แปลงจาก σ เป็นค่าความเที่ยงตรง
x = [] # ลิสต์เก็บค่าที่สุ่มได้ทั้งหมด
for n in range(21):
    # คำนวณค่า ν และ β ใหม่ในแต่ละรอบ
    ν = ν0+n/2
    β = β0+sum((xi-μ)**2/2 for xi in x)
    α_max = (ν-1)/β # หาจุดสูงสุด
    print('n=%d, ν=%.2f, β=%.2f, α_max=%.2f'%(n,ν,β,α_max))
    # สุ่มค่าใหม่ในแต่ละรอบ
    x += [random.gauss(μ,σ)]

ผลที่ได้

n=0, ν=1.00, β=0.01, α_max=0.00
n=1, ν=1.50, β=0.55, α_max=0.91
n=2, ν=2.00, β=0.55, α_max=1.80
n=3, ν=2.50, β=0.56, α_max=2.70
n=4, ν=3.00, β=1.32, α_max=1.51
n=5, ν=3.50, β=1.36, α_max=1.84
n=6, ν=4.00, β=1.45, α_max=2.06
n=7, ν=4.50, β=9.46, α_max=0.37
n=8, ν=5.00, β=11.80, α_max=0.34
n=9, ν=5.50, β=12.79, α_max=0.35
n=10, ν=6.00, β=13.37, α_max=0.37
n=11, ν=6.50, β=17.01, α_max=0.32
n=12, ν=7.00, β=17.28, α_max=0.35
n=13, ν=7.50, β=17.91, α_max=0.36
n=14, ν=8.00, β=17.93, α_max=0.39
n=15, ν=8.50, β=18.33, α_max=0.41
n=16, ν=9.00, β=24.77, α_max=0.32
n=17, ν=9.50, β=25.38, α_max=0.33
n=18, ν=10.00, β=25.44, α_max=0.35
n=19, ν=10.50, β=35.43, α_max=0.27
n=20, ν=11.00, β=39.57, α_max=0.25

เมื่อนำมาแสดงเป็นภาพเคลื่อนไหวจะได้แบบนี้



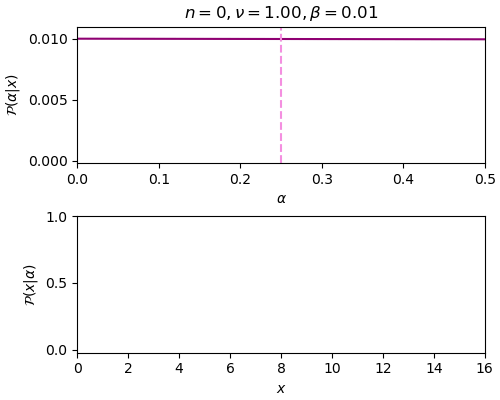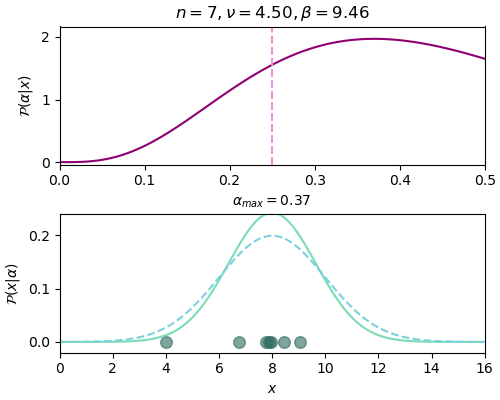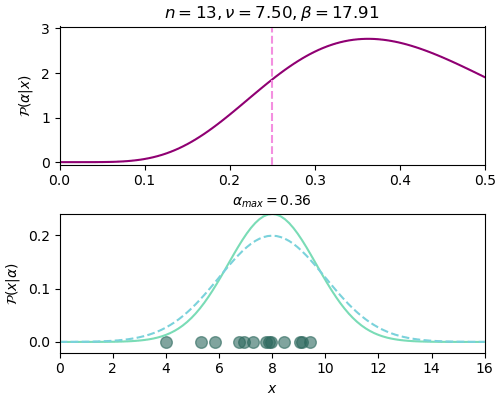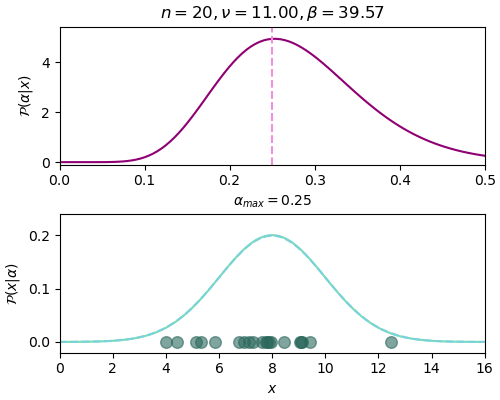
ภาพด้านบนแสดงการแจกแจงของ α จะเห็นว่ายิ่งเพิ่มข้อมูล ตำแหน่ง α ที่ค่าสูงสุดก็ยิ่งลู่เข้าตำแหน่งเส้นประสีชมพู คือ α=0.25 ซึ่งเป็นค่าจริง และกราฟการแจกแจงก็ค่อยๆบีบแคบลงมา

ส่วนภาพด้านล่างแสดงจุดตำแหน่งของข้อมูลที่สุ่มได้ และเส้นกราฟแสดงการแจกแจงของค่า x โดยเส้นประสีฟ้าคือค่าจริง ส่วนเส้นเขียนคือค่าที่ใช้ α สูงสุดจากการแจกแจงในแต่ละรอบซึ่งเปลี่ยนไปเรื่อยๆเมื่อได้ข้อมูลเข้ามา ยิ่งผ่านไปกราฟทั้งสองก็ยิ่งใกล้เคียงกัน นั่นคือเราสามารถหาค่า α ได้ใกล้เคียงค่าจริง

สำหรับการแจกแจงแบบปกติหลายตัวแปรจะทำคล้ายกันแต่จะใช้การแจกแจงวิชาร์ตเป็นความน่าจะเป็นก่อนหน้าสังยคแทน ซึ่งเขียนถึงในบทที่ ๑๗


การแจกแจงความน่าจะเป็นของพารามิเตอร์ของการแจกแจงแบบเลขชี้กำลัง

ต่อไปมาดูกรณีของการแจกแจงแบบเลขชี้กำลัง ซึ่งใช้การแจกแจงแกมมาเป็นความน่าจะเป็นก่อนหน้าสังยุคเช่นกัน

ในที่นี้ขอเขียนแทนการแจกแจงแบบเลขชี้กำลังด้วย $\mathcal{E}\mathscr{x̉}$ แบบนี้


ค่าพารามิเตอร์ที่พิจารณาคราวนี้คือ λ

เนื่องจากขั้นตอนต่างๆก็จะคล้ายกับที่ทำไปในกรณีการแจกแจงแบบปกติ ต่อไปนี้จะอธิบายแค่คร่าวๆอย่างรวบรัด

รายละเอียดเกี่ยวกับการแจกแจงแบบเลขชี้กำลังอ่านได้ในบทที่ ๑๐

เมื่อมีค่า x₁ ซึ่งได้จากการสุ่มด้วยการแจกแจงแบบเลขชี้กำลัง ฟังก์ชันควรจะเป็นคือ


ให้การแจกแจงความน่าจะเป็นก่อนหน้าเป็นค่าคงตัว


แล้วก็จะคำนวณความน่าจะเป็นภายหลังได้ในรูปของการแจกแจงแกมมาตามนี้


และถ้ามีข้อมูลจากการสุ่มอยู่ n ตัว ก็จะได้ผลตามนี้


โดย ν จะเพิ่มขึ้นทีละ 1 ตามจำนวนข้อมูล และ β จะเป็นผลรวมของค่า

หากเตรียมความน่าจะเป็นก่อนหน้าเป็นฟังก์ชันแกมมาซึ่งมีค่าเริ่มต้น νเป็นν₀ และ β เป็น ₀


ก็จะได้การแจกแจงความน่าจะเป็นภายหลังของ λ เป็น




ตัวอย่าง ลองทำการสุ่มจริงแล้วหาการแจกแจงความน่าจะเป็นของพารามิเตอร์ λ จากข้อมูลที่ได้ซึ่งเพิ่มขึ้นเรื่อยๆในแต่ละขั้น

ν0 = 1 # ν เริ่มต้น
β0 = 0.01 # β เริ่มต้น
λ = 20 # λ จริงๆของการแจกแจง
# สุ่มค่า t
t = []
for i in range(100*λ):
    t += [random.uniform(0,100)]
t = sorted(t) # จัดเรียงใหม่
n = 0
x = [] # ลิสต์เก็บค่าระยะห่างระหว่าง t
for i in range(13):
    # คำนวณค่า ν และ β ใหม่ในแต่ละรอบ
    ν = ν0+n
    β = β0+sum(x)
    λ_max = (ν-1)/β # λ ที่ค่าสูงที่สุด
    print('n=%d, ν=%d, β=%.2f, λ_max=%.2f'%(n,ν,β,λ_max))
    
    # เอาค่า t ที่สุ่มได้มาเทียบระยะห่างทีละคู่
    for j in range(24):
        x += [t[n+1]-t[n]]
        n += 1

ผลที่ได้

n=0, ν=1, β=0.01, λ_max=0.00
n=24, ν=25, β=1.17, λ_max=20.54
n=48, ν=49, β=2.68, λ_max=17.91
n=72, ν=73, β=4.38, λ_max=16.44
n=96, ν=97, β=5.30, λ_max=18.10
n=120, ν=121, β=6.38, λ_max=18.80
n=144, ν=145, β=8.29, λ_max=17.37
n=168, ν=169, β=9.57, λ_max=17.55
n=192, ν=193, β=10.44, λ_max=18.40
n=216, ν=217, β=11.75, λ_max=18.38
n=240, ν=241, β=12.70, λ_max=18.89
n=264, ν=265, β=13.73, λ_max=19.23
n=288, ν=289, β=14.70, λ_max=19.59

ทำเป็นภาพเคลื่อนไหวได้แบบนี้



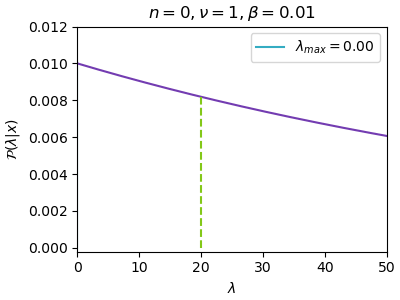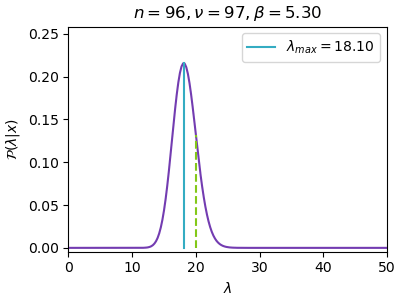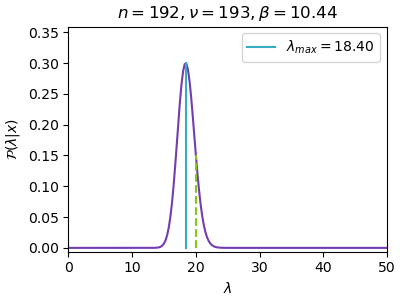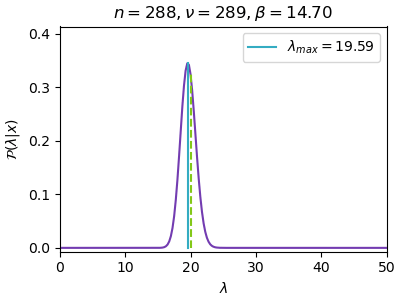
เส้นสีฟ้าคือจุดสูงสุดที่หาได้ขณะนั้น ส่วนเส้นประสีเขียวคือที่ λ=20 ซึ่งเป็นค่าจริง

ยิ่งใช้ผลการสุ่มหลายค่ามาก การแจกแจงก็ยิ่งบีบแคลลงโดยไปกองรวมที่ λ=20




การแจกแจงความน่าจะเป็นของพารามิเตอร์ของการแจกแจงปัวซง

สุดท้ายมาดูกรณีของการแจกแจงปัวซง ซึ่งใช้การแจกแจงแกมมาเป็นความน่าจะเป็นก่อนหน้าสังยุคเช่นกัน

รายละเอียดเกี่ยวกับการแจกแจงปัวซงอ่านได้ในบทที่ ๗

ในที่นี้จะเขียนแทนการแจกแจงปัวซงด้วย $\mathcal{Pő}$ ดังนี้


พารามิเตอร์ของการแจกแจงปัวซงก็คือค่า λ

ให้ข้อมูล k₁ ซึ่งมีการแจกแจงแบบปัวซง ฟังก์ชันควรจะเป็นคือ


เมื่อให้การแจกแจงความน่าจะเป็นก่อนหน้าเป็นค่าคงตัว


ก็จะได้การแจกแจงภายหลังดังนี้


เมื่อมีข้อมูล n ตัวก็จะได้เป็น


จะเห็นว่าตรงกันข้ามกับกรณีของการแจกแจงแบบเลขชี้กำลัง โดย ν จะเพิ่มขึ้นตามผลรวมของค่าของข้อมูล ส่วน β จะเพิ่มตามจำนวนข้อมูล

กรณีที่ให้ความน่าจะเป็นก่อนหน้าเป็นฟังก์ชันแกมมาที่มีพารามิเตอร์เริ่มต้นเป็น ν₀ และ β₀


ก็จะได้การแจกแจงความน่าจะเป็นภายหลังดังนี้


ตัวอย่าง ทำการสุ่มข้อมูลให้มีการแจกแจงแบบปัวซง ค่อยๆเพิ่มข้อมูลเข้ามาทีละนิดแล้วดูความเปลี่ยนแปลงของการแจกแจงความน่าจะเป็นของค่า λ ที่ทำนายได้

ν0 = 1 # ค่า ν เริ่มต้น
β0 = 0.5 # ค่า β เริ่มต้น
λ = 4 # ค่า λ จริงๆของการแจกแจง
k = [0]*300
for i in range(300*λ):
    k[random.randint(0,299)] += 1

for i in range(11):
    n = i*30 # จำนวนข้อมูลที่จะใช้ในรอบนั้นๆ
    ν = ν0+sum(k[:n])
    β = β0+n
    λ_max = (ν-1)/β
    print('n=%d, ν=%d, β=%.1f, λ_max=%.3f'%(n,ν,β,λ_max))

ผลที่ได้

n=0, ν=1, β=0.5, λ_max=0.000
n=30, ν=125, β=30.5, λ_max=4.066
n=60, ν=233, β=60.5, λ_max=3.835
n=90, ν=346, β=90.5, λ_max=3.812
n=120, ν=468, β=120.5, λ_max=3.876
n=150, ν=610, β=150.5, λ_max=4.047
n=180, ν=737, β=180.5, λ_max=4.078
n=210, ν=850, β=210.5, λ_max=4.033
n=240, ν=969, β=240.5, λ_max=4.025
n=270, ν=1090, β=270.5, λ_max=4.026
n=300, ν=1201, β=300.5, λ_max=3.993

นำมาวาดเป็นภาพเคลื่อนไหวแสดงแต่ละขั้นตอนได้ดังนี้



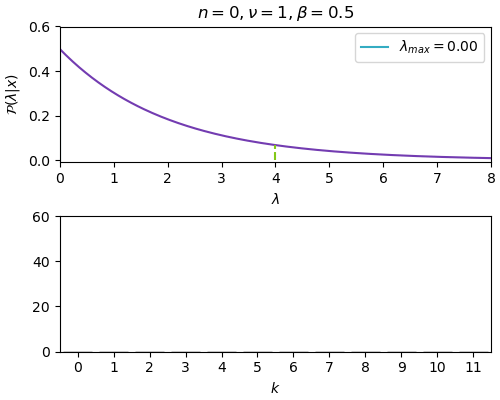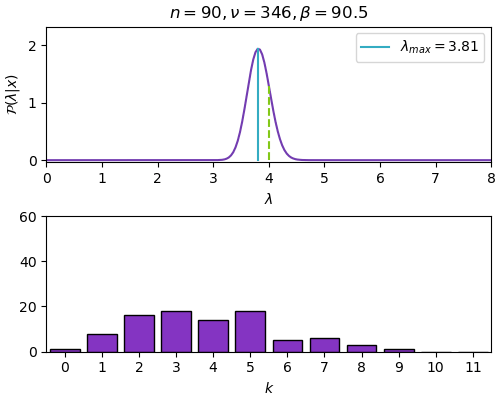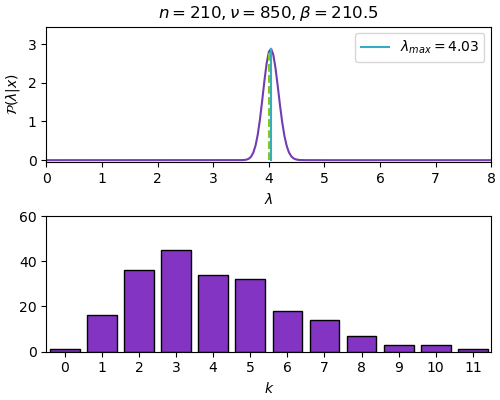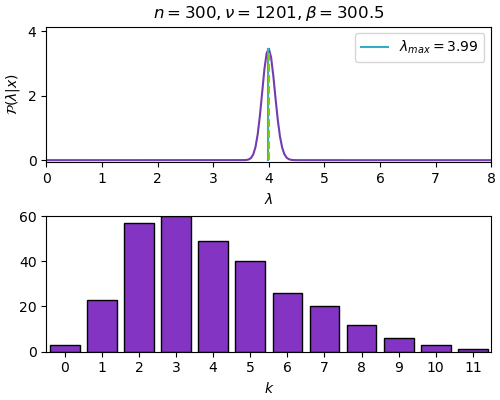
ในที่นี้ภาพด้านบนคือการแจกแจงของค่า λ ส่วนภาพด้านล่างคือจำนวนรวมของค่า k แต่ละค่า ซึ่งรวมกันทั้งหมดเท่ากับ n แต่ละขั้นให้เพิ่ม n ทีละ 30

เมื่อข้อมูลเพิ่มมากขึ้นก็จะหาจุดสูงสุดได้ใกล้เคียงค่าจริงคือที่ λ=4 และการแจกแจงก็จะบีบแคบลง



บทถัดไป >> บทที่ ๑๗

~ 自己紹介 ~

目次

日本による名言集

python モジュール -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 機械学習 -- ニューラル      ネットワーク

javascript

モンゴル語

言語学

maya

確率論

日本での日記

中国での日記 -- 北京での日記 -- 香港での日記 -- 澳門での日記

台灣での日記

北欧での日記

他の国での日記

qiita

その他の記事

記事の類別

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --MATLAB --SQL --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม --สเตเบิลดิฟฟิวชัน ---comfyui -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ -ซางะ -นางาซากิ -คุมาโมโตะ -โออิตะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ -ออสเตรเลีย ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -ภูเขาไฟ -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม เรื่องแต่ง บันทึก

　 記事を検索

　 最新記事

　 おすすめの記事

月別記事

もっと前の記事

ไทย

日本語

中文