เข้าใจ MCMC แบบรวบรัด

มอนเตการ์โลห่วงโซ่มาร์คอฟ (马尔可夫链蒙特卡洛, Markov chain Monte Carlo) หรือนิยมเรียกย่อๆว่า MCMC เป็นวิธีการสุ่มตัวอย่างชนิดหนึ่งที่เป็นที่นิยมใช้อย่างมาก

ในบทความก่อนหน้านี้ได้เขียนถึงเรื่องที่ว่าการสร้างค่าสุ่มให้แจกแจงในแบบที่ต้องการนั้นไม่ใช่เรื่องง่าย มีวิธีการต่างๆมากมาย ซึ่งที่เป็นพื้นฐานก็ได้แก่

- วิธีการยอมรับและปฏิเสธ (คัดเอาหรือคัดทิ้ง) ซึ่งเข้าใจง่าย ใช้งานได้ทั่วไป แต่มักจะประสิทธิภาพต่ำจนไม่เหมาะใช้งานจริง โดยเฉพาะกับข้อมูลหลายมิติ

- วิธีการแปลงผกผัน ซึ่งเป็นวิธีที่มีประสิทธิภาพที่สุดเมื่อใช้กับการแจกแจงแบบต่อเนื่องบางส่วนที่ใช้วิธีนี้ได้ แต่จำเป็นต้องรู้ฟังก์ชันผกผันของความน่าจะเป็นสะสม ซึ่งโดยมากแล้วอาจหาไม่ได้ง่ายๆ จึงไม่ใช่ว่าจะใช้ได้ทั่วไป

- ถ้าเป็นการแจกแจงในแบบที่พบได้บ่อยถูกใช้มากอยู่แล้วมักมีอยู่ในมอดูล scipy.stats หากมีก็ใช้อันนี้จะเป็นวิธีที่ดีที่สะดวกที่สุด

ส่วน MCMC นั้นก็เป็นอีกวิธีหนึ่งที่ถูกคิดขึ้นมาเพื่อใช้ในการสร้างค่าสุ่มให้มีการแจกแจงเป็นไปตามที่ต้องการ ซึ่งหลังๆมานี้ได้รับความสนใจมากเพราะว่าใช้งานได้ทั่วไป คือใช้กับการแจกแจงแบบไหนก็ได้ขอแค่ทราบฟังก์ชันการแจกแจง และนอกจากนี้ก็มีประสิทธิภาพดีด้วย แม้แต่กับข้อมูลที่มีหลายมิติ

แต่ว่าหลักการของ MCMC นั้นค่อนข้างเข้าใจยากและมีรายละเอียดมาก โดยมีพื้นฐานมาจากวิธีการมอนเตการ์โล (蒙特卡洛方法, Monte Carlo method) และห่วงโซ่มาร์คอฟ (马尔可夫链, Markov chain) ซึ่งวิธีพิสูจน์ต้องอาศัยความเข้าใจเรื่องความน่าจะเป็นพอสมควร

ในบทความนี้จะอธิบายวิธีการใช้ MCMC อย่างง่ายๆโดยยังไม่พูดถึงหลักการว่ามันทำงานยังไง ทำไมทำแบบนี้แล้วถึงได้ค่าสุ่มในแบบที่ต้องการได้ เหมาะกับคนที่ต้องการใช้งาน แต่ไม่ได้คิดจะรู้ลึก เพราะการเข้าใจว่าอะไรใช้งานอย่างไรนั้นมักจะง่ายกว่าการเข้าใจว่ามันทำงานได้อย่างไร

ในที่นี้จะให้มองข้ามรายละเอียดว่า "อะไรคือห่วงโซ่มาร์คอฟ?" "อะไรคือมอนเตการ์โล?" แค่ให้เข้าใจว่ารวมกันแล้วกลายเป็น "มอนเตการ์โลห่วงโซ่มาร์คอฟ" ซึ่งเป็นวิธีการหนึ่งที่ใช้ในการสร้างค่าสุ่ม

และที่จริง MCMC ยังไม่ใช่แค่ตัวสร้างค่าสุ่ม แต่ยังถูกเอาไปประยุกต์ต่อยอดใช้งานมากกว่านั้น รวมถึงในสาขาการเรียนรู้ของเครื่องด้วย

สำหรับรายละเอียดเบื้องลึกเพื่อความเข้าใจโดยละเอียดจริงๆจะอธิบายแยกในบทความหลังจากนี้อีกที




วิธีการเมโทรโพลิส

วิธีการที่เรียกว่า MCMC นั้นจริงๆเป็นวิธีที่เรียกรวมๆหลายวิธี ซึ่งต่างกันไปในรายละเอียด แต่วิธีที่เป็นพื้นฐานและเข้าใจได้ง่ายที่สุดก็คือวิธีการเมโทรโพลิส (梅特罗波利斯方法, Metropolis method) ซึ่งเป็นเป็นกรณีพิเศษของวิธีที่เรียกว่าวิธีการเมโทรโพลิส-เฮสติงส์ (梅特罗波利斯－黑斯廷斯方法, Metropolis–Hastings method) อีกที

ในที่นี้จะขอข้ามเรื่องการพิสูจน์ แต่จะมุ่งไปที่การอธิบายขั้นตอนวิธีใช้งาน

สมมุติว่ามีฟังก์ชันการแจกแจงความน่าจะเป็นที่ต้องการ f(x) อยู่ ซึ่งต้องการที่จะสร้างค่าสุ่มให้ได้เป็นไปตามฟังก์ชันนี้ แต่ไม่สามารถทำได้โดยตรง แต่เรามีการแจกแจงอีกแบบคือ q(x) ซึ่งสุ่มได้ง่ายซึ่งมีวิธีที่จะสุ่มให้เป็นไปตามการแจกแจงนี้ได้และมีความสมมาตร คือค่าขึ้นกับระยะทางเท่านั้น (เช่นการแจกแจงเอกรูปหรือการแจกแจงแบบปกติ)

เราสามารถสร้างค่าสุ่มที่แจกแจงตาม f(x) ได้โดยการสุ่ม q(x) แทนโดยมีขั้นตอนโดยรวมดังนี้


จะเห็นว่าในแต่ละรอบมีการสุ่ม ๒ ครั้ง รอบแรกคือสุ่มตำแหน่งเป้าหมาย x' ตามการแจกแจง q(x) โดยมี x_t เป็นศูนย์กลาง และอีกครั้งคือกรณีที่ r<1 ให้สุ่มว่าจะเอาหรือทิ้งตำแหน่งเป้าหมาย โดยสุ่มค่า 0 ถึง 1 แล้วมาเทียบกับ r แต่ถ้า r≥1 อยู่แล้วก็ถือว่าย้ายแน่นอน ไม่ต้องทำการสุ่ม

เมื่อทำแบบนี้แล้วจะได้ตำแหน่งใหม่จากการสุ่มไปเรื่อยๆโดยสัดส่วนการแจกแจงที่เป็นไปตาม f(x)

ด้วยวิธีนี้ทำให้แม้ค่าที่เราทำการสุ่มไปจริงๆคือการแจกแจง q(x) ไม่ได้สุ่ม f(x) โดยตรง แต่ผลที่ได้จะออกมามีการแจกแจงเต็มไปตาม f(x)

ที่จริงแล้ว f(x) นั้นได้ถูกใช้แค่ตอนที่พิจารณาค่า r เพื่อตัดสินว่าจะย้ายไปตำแหน่งเป้าหมายหรือไม่

แม้เราจะไม่ได้สุ่มด้วย f(x) โดยตรง แต่การพิจารณาในจุดนี้เองที่เป็นตัวทำให้การแจกแจงเป็นไปตาม f(x) ได้ เพราะยิ่งตำแหน่งที่ f(x) มากก็ยิ่งมีโอกาสย้ายไปถึงมาก แต่ถ้า f(x) น้อย โอกาสไปถึงก็น้อย

ฟังแล้วอาจชวนให้แปลกใจว่าทำตามวิธีการแบบนี้แล้วจะทำให้ได้ค่าสุ่มตามการแจกแจง f(x) ได้จริงหรือ ซึ่งอันนี้ก็สามารถพิสูจน์ได้ แต่จะยังไม่พูดถึงในที่นี้ ให้เชื่อไปก่อนว่าวิธีนี้ได้ผลจริงๆ




MCMC ในหนึ่งมิติ

หลังจากเข้าใจวิธีการไปแล้ว ขั้นต่อไปก็คือลงมือปฏิบัติโดยเขียนโค้ดจริงๆเพื่อพิสูจน์ว่าวิธีนี้ใช้การได้จริงๆ โดยขอเริ่มจากกรณีมิติเดียวซึ่งเข้าใจได้ง่ายๆก่อน

ก่อนอื่น สมมุติว่าฟังก์ชันแจกแจงที่เป็นเป้าหมายที่ต้องการคือฟังก์ชันที่สร้างยากแบบนี้


ลองสร้างฟังก์ชันขึ้นมาในไพธอนแล้ววาดกราฟดู

import matplotlib.pyplot as plt
import numpy as np

def f_paomai(x):
    return np.where(x>=5,np.where(x<10,(x-10)**2,0),np.where(x>0,x**2,0))/250*3

x = np.linspace(0,10,101)
y = f_paomai(x)
plt.xlabel('x')
plt.plot(x,y,c='#055b25')
plt.grid(ls='--')
plt.show()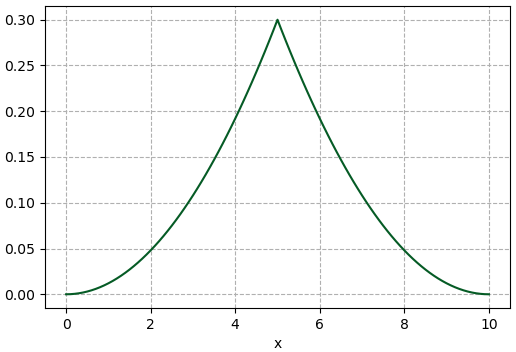

ต่อไปก็ฟังก์ชันการแจกแจง q(x) ซึ่งเป็นการแจกแจงที่เราสามารถสร้างขึ้นได้ง่ายๆ ซึ่งถ้าพูดถึงสร้างง่ายๆแล้ว แน่นอนว่าคือการแจกแจงเอกรูป ในที่นี้จะใช้ตามนี้


โดย x_t เป็นจุดกึ่งกลาง ซึ่งก็คือตำแหน่ง x ปัจจุบันก่อนที่จะย้าย ส่วน σ เป็นค่าความกว้างซึ่งถือเป็นไฮเพอร์พารามิเตอร์ตัวหนึ่งที่ต้องกำหนดขึ้นเองตามความเหมาะสม

ในที่นี้จะให้ σ=2

เขียนโค้ดทำ MCMC เมโทรโพลิสดูได้ดังนี้

# วาดกราฟฟังก์ชัน f(x)
x = np.linspace(0,10,101)
y = f_paomai(x)
plt.xlabel('x')
plt.plot(x,y,c='#553a25')

x = [1] # จุดเริ่มต้น
for _ in range(100000):
    x0 = x[-1] # ตำแหน่ง x เดิม
    x1 = x0 + np.random.uniform(-1,1) # สุ่มตำแหน่ง x เป้าหมาย
    # คำนวณ f(x) ที่จุดเดิมและจุดเป้าหมาย
    f0 = f_paomai(x0)
    f1 = f_paomai(x1)
    r = f1/f0 # คำนวณ r
    # ถ้า r>1 ให้เอาค่าเป้าหมายเป็นค่าใหม่ แต่ถ้า r<1 ให้สุ่มค่าเพื่อตัดสินว่าจะเอาค่าใหม่หรือไม่
    if(r<1 or r>np.random.random()):
        # ถ้าตัดสินใจเอาค่าเป้าหมายเป็นค่าใหม่
        x.append(x1)
    else:
        # ถ้าไม่เอาค่าเป้าหมายก็ใช้ค่าเดิมมาเป็นค่าใหม่ซ้ำต่ออีก
        x.append(x0)

# แสดงการแจกแจงเป็นฮิสโตแกรมความหนาแน่น
plt.hist(x,np.linspace(0,10,61),density=1,fc='#fdde7d',ec='k')
plt.grid(ls='--')
plt.show()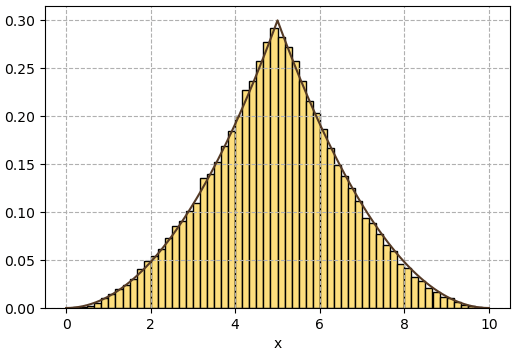

ผลที่ได้จะเห็นว่าการแจกแจงเป็นไปตามการแจกแจงที่ต้องการจริงๆ

แต่ผลที่ได้ก็ไม่ได้ออกมาเป็นไปอย่างที่ต้องการเสมอไป ซึ่งขึ้นอยู่กับปัจจัยต่างๆ เช่นตำแหน่ง x เริ่มต้น และการแจกแจง q ที่เราเลือกใช้สุ่ม หากผลการสุ่มออกมาไม่เป็นตรงกับที่ควรจะเป็นก็อาจลองปรับตำแหน่งเริ่มต้นหรือฟังก์ชันการแจกแจงดู โดยทั่วไปแล้วควรให้ส่วนเบี่ยงเบนมาตรฐานของการแจกแจง q ใกล้เคียงกับ f จะดีกว่า ไม่ควรให้มากหรือน้อยกว่าจนเกินไป

ในตัวอย่างนี้ใช้ฟังก์ชันการแจกแจงเป็นแบบเอกรูป แต่ก็อาจใช้การแจกแจงอื่นๆที่มีความสมมาตรเหมือนกัน ที่นิยมใช้มากคือการแจกแจงแบบปกติ ซึ่งก็เป็นการแจกแจงพื้นฐานอีกอย่างที่สร้างได้ง่ายและใช้อยู่ทั่วไป




การตัดช่วงระยะทดลอง

ปัญหาอย่างหนึ่งของ MCMC ก็คือข้อมูลในช่วงต้นๆที่เริ่มสุ่มนั้นจะขึ้นอยู่กับตำแหน่งเริ่มต้น การแจกแจงจะยังไม่ได้เป็นไปตามฟังก์ชันเป้าหมาย จนกว่าจะผ่านไปสักระยะหนึ่ง ซึ่งบางครั้งมักจะมีการตัดช่วงต้นนี้ทิ้งไป

ช่วงตรงต้นที่ถูกตัดทิ้งนี้มักถูกเรียกว่า burn-in ซึ่งคำนี้เดิมเป็นศัพท์ที่ใช้เรียกระยะทดลองของอุปกรณ์อิเล็กทรอนิกส์ ซึ่งต้องมีช่วงแรกๆเป็นระยะทดลองจนกว่าจะเริ่มเข้าที่เข้าทางแล้วเหมาะจะใช้ได้จริงๆ

เพื่อที่จะดูว่าช่วงไหนที่ควรจะต้องตัดทิ้ง อาจลองพิจารณาโดยวาดกราฟแสดงค่าเฉลี่ยของค่าทั้งหมดที่สุ่มได้จนถึงขั้นนั้น

ยกตัวอย่างเช่น MCMC ที่เขียนในตัวอย่างที่แล้ว ถ้าเอาช่วง 10000 ขั้นแรกมาลองวาดกราฟค่าเฉลี่ยดูก็จะได้ดังนี้

n = np.arange(1,10000+1)
plt.xlabel('จำนวนรอบ',family='Tahoma')
plt.ylabel(r'$\bar{x}$')
plt.plot(n,np.cumsum(x[:10000])/n,c='#d9a048')
plt.grid(ls='--')
plt.show()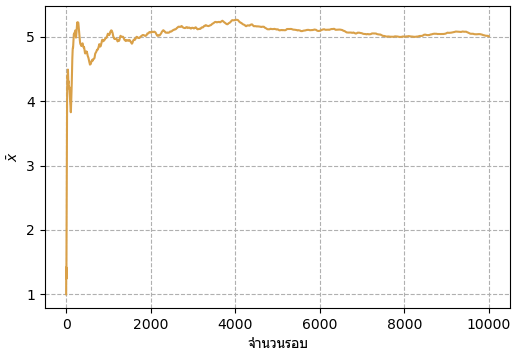

เนื่องจากเริ่มต้นจาก x=1 ค่าในช่วงแรกจะเอียงไปทางแถวนั้นมาก แต่จะค่อยๆเข้าใกล้ค่าที่เป็นค่าเฉลี่ยของการแจกเข้าไปเรื่อยๆ ในที่นี้คือ x=5 จากในรูปนี้ดูแล้วอาจพิจารณาตัดช่วง 3000 แรกทิ้งไป

แต่จำนวนในช่วงต้นที่ต้องตัดทิ้งนั้นจะมีจำนวนเป็นเท่าไหร่ก็ไม่ใช่อะไรที่ตายตัว ขึ้นอยู่กับฟังก์ชันเป้าหมาย แล้วยังขึ้นอยู่กับจุดเริ่มต้นที่ใช้สุ่มด้วย

โดยรวมแล้วการสุ่มด้วย MCMC วิธีการเมโทรโพลิสนี้จะมีการทิ้งข้อมูลที่สุ่มไปจำนวนหนึ่ง ทั้งค่าช่วงต้นในระยะทดลอง และค่าที่คัดทิ้งในตอนที่เคลื่อนไปตำแหน่งที่ความน่าจะเป็นน้อยลง

แต่หากเทียบกับบางวิธีเช่นวิธีการยอมรับและปฏิเสธ (คัดเอาหรือคัดทิ้ง) ซึ่งต้องมีการทิ้งตัวอย่างไปจำนวนมากแล้ว ก็ถือว่าทิ้งน้อยกว่ามาก โดยเฉพาะยิ่งกรณีที่ใช้กับหลายมิติก็จะยิ่งเห็นความแตกต่างได้ชัดขึ้น




MCMC ในสองมิติ

เมื่อเข้าใจวิธีการทำในหนึ่งมิติแล้ว ต่อมาก็มาดูกรณีหลายมิติ โดยเริ่มจากสองมิติก่อน

วิธีการโดยรวมแล้วเหมือนเดิม แต่ครั้งนี้เปลี่ยนจาก x ที่เป็นมิติเดียวไปเป็น X ซึ่งมีหลายมิติ

ลองให้ฟังก์ชันการแจกแจงความน่าจะเป็นเป็นฟังก์ชันยากๆดังนี้ โดยแจกแจงสองมิติให้ X เป็น x,y


* อนึ่ง ฟังก์ชันแจกแจงตัวนี้ให้ค่าที่ยังไม่ได้ทำการนอร์มาไลซ์ให้ความน่าจะเป็นรวมกันแล้วได้ 1 แต่จริงๆแล้วก็ไม่จำเป็น เพราะสิ่งสำคัญคือสัดส่วนว่าความน่าจะเป็นที่ไหนมากหรือน้อยเป็นกี่เท่าของที่ไหน

ลองเขียนโค้ดแสดงคอนทัวร์บอกค่าความหนาแน่นความน่าจะเป็นดูว่าหน้าตาเป็นยังไง

def f_paomai(x,y):
    return np.exp(-(3*x**2+y**2)/20)*(1+np.cos((x**2+2*y**2)/4))*(x**2)

x,y = np.meshgrid(np.linspace(-10,10,101),np.linspace(-10,10,101))
plt.figure(figsize=[6,5])
plt.axes(aspect=1)
plt.contourf(x,y,f_paomai(x,y),100,cmap='plasma')
plt.colorbar(pad=0.01)
plt.show()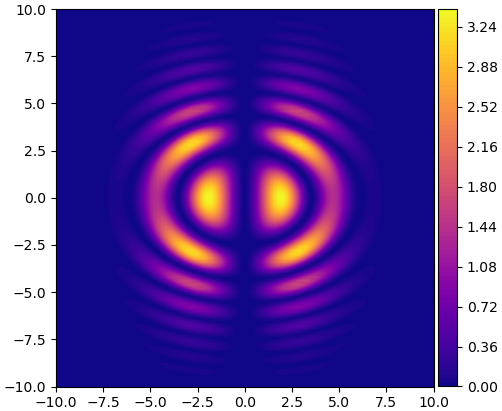

ใช้ MCMC เพื่อทำการสุ่มตัวอย่างค่า x,y โดยคราวนี้ก็ใช้ฟังก์ชันการสุ่ม q(x,y) เป็นการแจกแจงแบบเอกรูปเช่นกัน แต่คราวนี้มี ๒​ ตัวแปร กำหนดขอบเขตให้อยู่ใน ±3 ทั้งในแกน x และ y


โดยที่ x_t,y_t คือจุดที่อยู่ปัจจุบัน ซึ่งให้ใช้เป็นจุดกึ่งกลางของการแจกแจง

เขียนโค้ดทำการสุ่มตัวอย่างโดย MCMC เมโทรโพลิสได้ดังนี้

X = [np.array([2,3])] # จุดเริ่มต้น
for _ in range(100000):
    X0 = X[-1] # ตำแหน่ง x,y เดิม
    X1 = X0 + np.random.uniform(-3,3,2) # สุ่มตำแหน่ง x,y เป้าหมาย
    # คำนวณ f(x,y) ที่จุดเดิมและจุดเป้าหมาย
    f0 = f_paomai(*X0)
    f1 = f_paomai(*X1)
    r = f1/f0 # คำนวณ r
    # ใช้ค่า r ตัดสินว่าจะเอาค่าใหม่หรือไม่
    if(r>1 or r>np.random.random()):
        # ถ้าตัดสินใจเอาค่าเป้าหมายเป็นค่าใหม่
        X.append(X1)
    else:
        # ถ้าไม่เอาค่าเป้าหมายก็ใช้ค่าเดิมมาเป็นค่าใหม่ซ้ำต่ออีก
        X.append(X0)

x,y = np.array(X).T
plt.figure(figsize=[5,6])
plt.axes(aspect=1)
plt.scatter(x,y,s=4,alpha=0.1,c=np.random.random([100001,3]))
plt.tight_layout()
plt.show()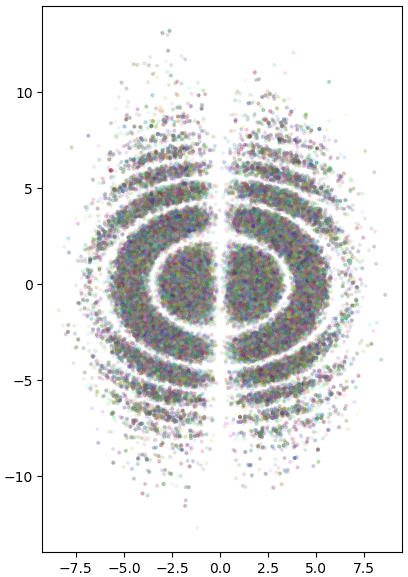

ลักษณะการแจกแจงเป็นไปตามความหนาแน่นดังที่แสดงในคอนทัวร์ดังที่ต้องการ

นี่เป็นตัวอย่างการใช้กับข้อมูลสองมิติ เมื่อเข้าใจหลักการแล้วก็สามารถนำไปใช้กับการแจกแจงในกี่มิติก็ได้ตามที่ต้องการ




สรุปทิ้งท้าย

ในบทความนี้ก็ได้แนะนำการใช้วิธีการมอนเตการ์โลห่วงโซ่มาร์คอฟ MCMC โดยข้ามรายละเอียดต่างๆไปมาก เพื่อแค่ต้องการให้เข้าใจภาพรวมและวิธีใช้เบื้องต้นเป็นหลัก

เกี่ยวกับ MCMC นั้นยังมีรายละเอียดอีกมากมายซึ่งถ้าจะใช้งานจริงๆอาจต้องศึกษาเพิ่มเติม

ยังมีเรื่องอีกมากมายเกี่ยวกับ MCMC ที่ยังจะต้องเขียนถึงต่อจากตรงนี้ไปอีก ทั้งเรื่องหลักการที่อยู่เบื้องหลังของวิธีการนี้ อย่างเรื่องของห่วงโซ่มาร์คอฟ และมิธีการมอนเตการ์โล ทั้งเรื่องวิธีอื่นนอกจากวิธีการเมโทโพลิสซึ่งเป็นวิธีง่ายสุดที่ได้กล่าวไป อีกทั้งยังวิธีการนำไปประยุกต์ใช้ในงานต่างๆด้วย



---------------

แหล่งอ้างอิง

~ 自己紹介 ~

目次

日本による名言集

python モジュール -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 機械学習 -- ニューラル      ネットワーク

javascript

モンゴル語

言語学

maya

確率論

日本での日記

中国での日記 -- 北京での日記 -- 香港での日記 -- 澳門での日記

台灣での日記

北欧での日記

他の国での日記

qiita

その他の記事

記事の類別

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --MATLAB --SQL --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม --สเตเบิลดิฟฟิวชัน ---comfyui -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ -ซางะ -นางาซากิ -คุมาโมโตะ -โออิตะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ -ออสเตรเลีย ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม เรื่องแต่ง บันทึก

　 記事を検索

　 最新記事

　 おすすめの記事

月別記事

もっと前の記事

ไทย

日本語

中文