วิธีการมอนเตการ์โล (蒙特卡洛方法, Monte Carlo method) เป็นอัลกอริธึมแบบหนึ่งที่นิยมใช้ในการแก้ปัญหาเชิงคำนวณ

ชื่อเรียกนี้จริงๆถูกใช้อย่างกว้างขวาง ซึ่งโดยรวมมักจะหมายถึงกลุ่มอัลกอริธึมที่อาศัยผลจากการสุ่มตัวอย่าง ซึ่งคำตอบที่ได้จะมีความไม่แน่นอน ต่างกันไปในแต่ละครั้งที่ทำการคำนวณ

และวิธีการมอนเตการ์โลก็เป็นพื้นฐานสำคัญของวิธีการมอนเตการ์โลห่วงโซ่มาร์คอฟ (MCMC) ซึ่งเป็นที่นิยมใช้มากในปัจจุบัน

ในบทความนี้จะเขียนถึงพื้นฐานของวิธีการมอนเตการ์โลส่วนหนึ่ง โดยยกตัวอย่างเรื่องการคำนวณหาปริพันธ์ และการหาค่า π




การหาปริพันธ์ด้วยวิธีการมอนเตการ์โล

ประโยชน์ใช้งานอย่างหนึ่งของวิธีการมอนเตการ์โลก็คือใช้หาปริพันธ์ของฟังก์ชันบางอย่างที่ไม่อาจแก้ได้ง่ายๆ

เช่นสมมุติว่ามีฟังก์ชัน f(x) เป็นฟังก์ชันอะไรบางอย่างที่ยุ่งๆเช่นแบบนี้


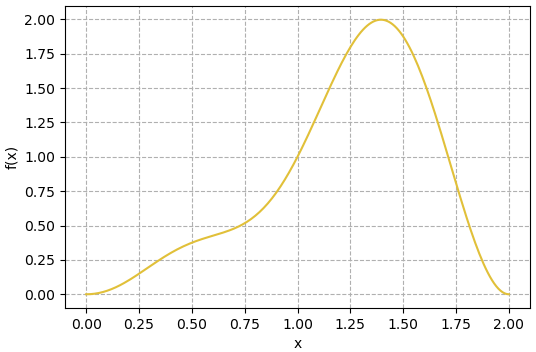
หากต้องการหาปริพันธ์ โดยทั่วไปก็จะคำนวณดังนี้


แต่ว่าถ้า f(x) ไม่อาจคำนวณปริพันธ์ได้ในเชิงวิเคราะห์ เพราะยุ่งเกินไป แบบนั้นก็ได้แต่ใช้วิธีเชิงคำนวณ

หากใช้วิธีการมอนเตการ์โล อาจหาปริพันธ์ได้โดยทำโดยสุ่มค่า x ซึ่งมีการแจกแจงความน่าจะเป็นเป็น $\mathcal{P}(x)$ ขึ้นมาทั้งหมด n ค่า แล้วคำนวณ


โดยการแจกแจง $\mathcal{P}$ นั้นจะใช้เป็นการแจกแจงแบบไหนก็ได้ที่เราสามารถสุ่มขึ้นมาได้จริงง่ายๆ ถ้าให้ง่ายที่สุดก็คือการแจกแจงแบบเอกรูป คือให้เท่ากันทั้งหมดในพื้นที่ที่กำหนด

ขอลองยกตัวอย่างฟังก์ชันที่สามารถคำนวณจริงๆได้ เพื่อจะได้เปรียบเทียบผลลัพธ์ได้ เช่น


วาดเป็นกราฟออกมาดู

import matplotlib.pyplot as plt
import numpy as np

def f(x):
    return np.pi*np.sin(np.pi*x/3)

x = np.linspace(0,3,201)
fx = f(x)
plt.axes(xlabel='x',ylabel='f(x)')
plt.plot(x,fx,c='#63e')
plt.grid(ls='--')
plt.show()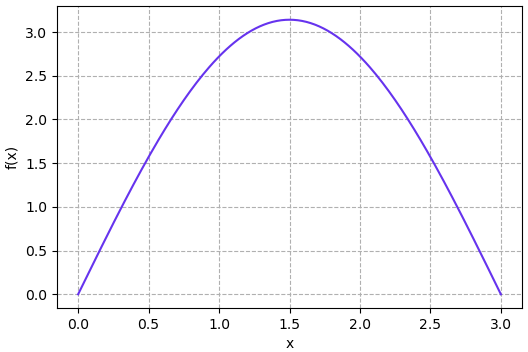

ลองหาปริพันธ์ตั้งแต่ 0 ถึง 3 ซึ่งจริงๆสามารถคำนวณออกมาได้ง่ายๆคือ


คราวนี้ลองหาด้วยวิธีการมอนเตการ์โล โดยการแจกแจงในที่นี้ก็ใช้ง่ายๆเป็นการแจกแจงเอกรูปในช่วง 0 ถึง 3


ก็จะคำนวณได้โดย


ลองเขียนโค้ดจำลองการหาคำนวณ โดยสุ่มสักแสนตัว

x = np.random.uniform(0,3,100000)
fx = f(x)
print(3*fx.mean()) # แสดงผลการคำนวณ

คำตอบออกมาควรจะได้ประมาณใกล้เคียงกับ 6 ซึ่งเป็นคำตอบจริงๆที่ควรจะเป็น

แต่เนื่องจากเป็นผลที่ได้จากการสุ่ม ย่อมมีความคลาดเคลื่อนอยู่ คำตอบที่ได้จึงไม่อาจเรียกได้ว่าเที่ยงตรง แต่สามารถเพิ่มความเที่ยงตรงได้โดยการเพิ่มตัวอย่างให้มากขึ้น

ลองดูผลลัพธ์ของตัวอย่างเดิมโดยเทียบค่าความคลาดเคลื่อนกำลังสองเมื่อเทียบกับจำนวนค่าที่ใช้ดู

n = np.arange(1,1+len(x))
plt.plot(n,((6-3*fx.cumsum()/n)**2),c='#63e')
plt.loglog() # แสดงสัดส่วนเป็นลอการิธึมทั้งสองแกน
plt.grid(ls='--')
plt.show()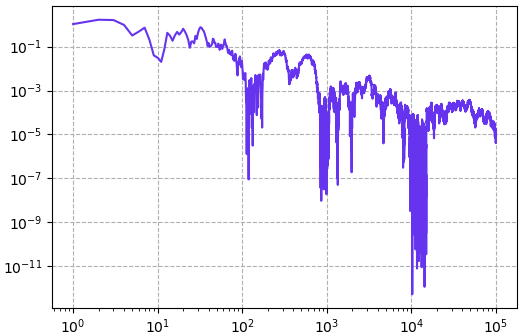

จะเห็นได้ว่ายิ่งเพิ่มจำนวนการสุ่มก็ยิ่งมีแนวโน้มจะแม่นขึ้นจริงๆ หากจำนวนมากเป็นอนันต์ผลที่ได้ก็จะมีความแน่นอน

ดังนั้นวิธีการนี้จะเห็นว่าแม้จะให้ผลลัพธ์ที่มีความไม่แน่นอนอยู่ แต่ก็ให้ผลดีขึ้นได้เมื่อจำนวนการสุ่มมากๆเข้า




การหาค่าไพจากพื้นที่วงกลมด้วยวิธีการมอนเตการ์โลในสองมิติ

ตัวอย่างที่แล้วเป็นกรณีหนึ่งมิติ คราวนี้ลองมาลองดูมอนเตการ์โลในสองมิติบ้าง ซึ่งตัวอย่างที่มักจะเจอบ่อยที่สุดเวลาพูดถึงวิธีการมอนเตการ์โลก็คือการหาค่า π จากพื้นที่วงกลม

สมมุติว่ามีข้อมูลสองมิติ x,y ปกติแล้วคำนวนปริพันธ์ได้ดังนี้


แต่ถ้าใช้วิธีการมอนเตการ์โลอาจคำนวณแบบนี้


สำหรับกรณีปัญหาพื้นที่วงกลมนั้นอาจพิจารณาฟังก์ชันลักษณะนี้


ให้การแจกแจงความน่าจะเป็นเป็น


เขียนโค้ดแสดงการคำนวณพร้อมวาดรูปประกอบได้ดังนี้

def f(x,y):
    return np.where(x**2+y**2<=1,1,0)

x = np.random.uniform(-1,1,10000)
y = np.random.uniform(-1,1,10000)
fxy = f(x,y)
plt.figure(figsize=[6,5])
plt.axes(aspect=1)
plt.scatter(x,y,c=fxy,ec='k',alpha=0.1,cmap='jet')
plt.grid(ls='--')
plt.tight_layout()
plt.show()
print(fxy.mean()/0.25) # แสดงค่าที่คำนวณได้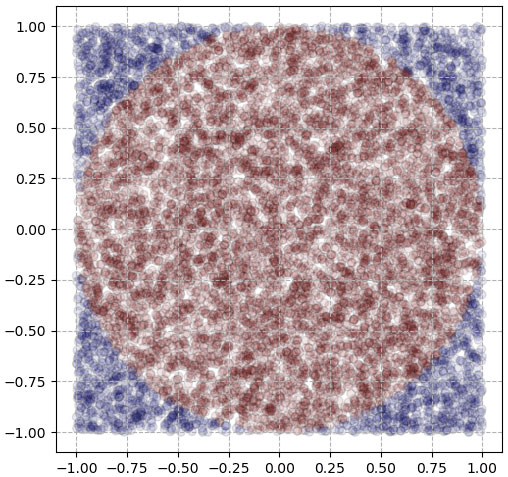

ในที่นี้พื้นที่สีแดงคือส่วนที่อยู่ในขอบเขตวงกลม คือส่วนที่จะให้มีค่าเป็น 1 ส่วนสีน้ำเงินอยู่ด้านนอก ให้เป็น 0 เมื่อหาค่าเฉลี่ยแล้วหารด้วยความน่าจะเป็นก็จะออกมาเป็นพื้นที่วงกลม ซึ่งในที่นี้ก็คือเท่ากับค่า π≈3.14

ผลที่ได้จากการคำนวณนี้ควรจะใกล้เคียงกับค่า 3.14




เทียบกับอัลกอริธึมเชิงกำหนดชัด

อัลกอริธึมที่ให้ผลไม่แน่นอนขึ้นอยู่กับการสุ่มอย่างวิธีการมอนเตการ์โลแบบนี้อาจเรียกว่าเป็นอัลกอริธึมเชิงไม่กำหนดชัด (非确定性算法, nondeterministic algorithm)

ซึ่งอาจนำไปเทียบกับอัลกอริธึมอีกแบบคือ เช่นหาพื้นที่ใต้กราฟโดยการแบ่งพื้นที่ออกเป็นช่วงๆย่อยๆ เช่นฟังก์ชันยุ่งๆในภาพนี้ ก็แบ่งเป็นแท่งๆแล้วคำนวณ



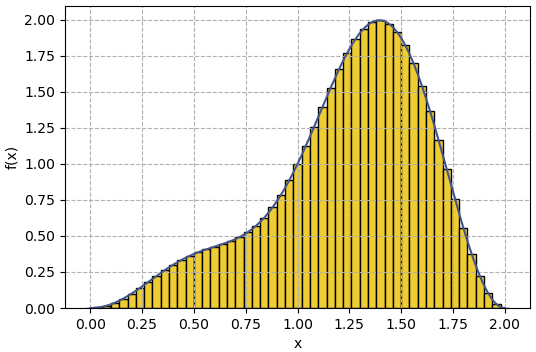
หรือรวมทั้งอาจทำเป็นสี่เหลี่ยมคางหมู (梯形, trapezoid) หรือซับซ้อนกว่านั้นก็เป็นวิธีรุงเงอ-คุททา (龙格－库塔法, Runge-Kutta method) ซึ่งยิ่งแบ่งละเอียดย่อยผลการคำนวณก็ยิ่งเที่ยงตรง อีกทั้งคำนวณทุกครั้งก็จะได้ผลแบบเดิมทุกครั้งแบบนี้เรียกว่าอัลกอริธึมเชิงกำหนดชัด (确定性算法, deterministic algorithm)

วิธีการมอนเตการ์โลนั้นมีการสุ่มและให้คำตอบไม่แน่นอน ซึ่งดูเผินๆแล้วเหมือนจะด้อยกว่าอัลกอริธึมเชิงกำหนดชัด

แต่หากลองพิจารณาปัญหาในหลายมิติ เช่นถ้าปริมาณมี m มิติ เมื่อทำการหาปริพันธ์ก็ต้องคำนวณทุกมิติแบบนี้


ถ้าจะทำการแบ่งเป็นช่วงย่อยๆแล้วคำนวณ มิติเดียวคงไม่มีปัญหาอะไร แต่เมื่อยิ่งมีมิติมากๆเข้าจำนวนช่วงที่แบ่งยิ่งเพิ่มมากอย่างรวดเร็ว

แต่ถ้าใช้วิธีการมอนเตการ์โล ไม่ว่าจะกี่มิติก็คำนวณเหมือนเดิม คือแค่คำนวณค่าฟังก์ชันและความน่าจะเป็นที่แต่ละตำแหน่งที่สุ่มได้นั้น โดยจำนวนการสุ่มก็ไม่ได้จำเป็นต้องเปลี่ยนไปตามจำนวนมิติที่เพิ่มขึ้น


จำนวนตัวอย่าง n เราเป็นคนกำหนดเอาเองได้ตามความเหมาะสม แน่นอนว่ายิ่ง n มากยิ่งเที่ยงตรง แต่ก็ไม่ได้มีความจำเป็นต้องเพิ่มมหาศาลแบบอย่างวิธีแบ่งช่วงคำนวณ

ดังนั้นข้อดีอย่างหนึ่งของวิธีการมอนเตการ์โลนั้นคือเมื่อเจอปัญหาที่มีจำนวนมิติมาก

แม้คำตอบที่ได้อาจมีความแม่แน่นอนอยู่ แต่ว่าในงานวิจัยทางวิทยาศาสตร์นั้นสถานการณ์แบบนี้ก็มีโอกาสเจออยู่มากมาย มอนเตการ์โลจึงเป็นวิธีหนึ่งที่ถูกใช้อย่างกว้างขวาง



แหล่งอ้างอิง

~ 自己紹介 ~

目次

日本による名言集

python モジュール -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 機械学習 -- ニューラル      ネットワーク

javascript

モンゴル語

言語学

maya

確率論

日本での日記

中国での日記 -- 北京での日記 -- 香港での日記 -- 澳門での日記

台灣での日記

北欧での日記

他の国での日記

qiita

その他の記事

記事の類別

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --MATLAB --SQL --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม --สเตเบิลดิฟฟิวชัน ---comfyui -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ -ซางะ -นางาซากิ -คุมาโมโตะ -โออิตะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ -ออสเตรเลีย ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -ภูเขาไฟ -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม เรื่องแต่ง บันทึก

　 記事を検索

　 最新記事

　 おすすめの記事

月別記事

もっと前の記事

ไทย

日本語

中文