โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๓: ฟังก์ชันกระตุ้นและการเคลื่อนลงตามความชัน
เขียนเมื่อ 2018/08/26 23:22
แก้ไขล่าสุด 2022/07/10 21:13
>> ต่อจาก บทที่ ๒
ในบทที่แล้วได้อธิบายหลักการเรียนรู้ปรับปรุงพารามิเตอร์ของเพอร์เซปตรอนอย่างง่ายไปแล้ว
วิธีการปรับพารามิเตอร์อย่างง่ายนั้นยังไม่ดีพอที่จะใช้งานจริง ดังนั้นในบทนี้จะเรียนรู้วิธีการที่นิยมนำมาใช้จริงๆภายในโครงข่ายประสาทเทียมในปัจจุบัน นั่นคือการใช้ฟังก์ชันกระตุ้น (激活函数, activation function)
ฟังก์ชันกระตุ้น
เดิมทีในอัลกอริธีมการปรับพารามิเตอร์ของเพอร์เซปตรอนแบบง่ายนั้นเมื่อนำค่าตัวแปรต้นคูณกับค่าน้ำหนักและบวกไบแอสแล้ว จะทำการทำนายคำตอบให้เป็น 0 หรือ 1 โดยพิจารณาว่าค่าเป็น 0 ขึ้นไปหรือไม่ นั่นคือ
..(3.1)
..(3.2)
โดย h คือค่าที่ทำนายได้ ซึ่งเราจะเอาค่านี้ไปเปรียบเทียบกับคำตอบจริง (z) เพื่อพิจารณาว่าควรปรับพารามิเตอร์เท่าไหร่
แต่ว่าถ้าคำนวณให้ h เป็นแค่ 0 หรือ 1 เท่านั้นแบบนี้ปัญหาคือมันจะไม่ได้บ่งบอกถึงระดับความผิดพลาดในการทำนาย แบบนี้ไม่ว่าค่าจะเกินหรือต่ำกว่าไปแค่ไหนก็จะถูกตัดสินแค่ว่าเป็น 0 หรือ 1 เหมือนกัน
ดังนั้นแทนที่จะตัดสินค่าทำนายเป็น 0 หรือ 1 ไปเลย จึงมีแนวคิดที่จะเปลี่ยนเป็นให้นำ a มาเข้าฟังก์ชันอะไรบางอย่าง เรียกฟังก์ชันนั้นว่าฟังก์ชันกระตุ้น
ฟังก์ชันกระตุ้นอาจเป็นอะไรก็ได้ที่มีลักษณะเป็นฟังก์ชันเพิ่ม (คือมีค่ามากเมื่อ x มาก และน้อยเมื่อ x น้อย x ที่ค่ามากกว่าจะต้องได้ค่าฟังก์ชันที่มากกว่าหรือเท่ากับค่า x ที่น้อยกว่าเสมอ)
ในการวิเคราะห์จำแนกประเภท ๒ กลุ่ม ฟังก์ชันกระตุ้นที่นิยมที่สุดคือฟังก์ชันซิกมอยด์ (sigmoid) นิยามดังนี้
..(3.3)
เมื่อนำฟังก์ชันนี้มาใช้เป็นฟังก์ชันกระตุ้นก็จะเขียนแทนสมการ (3.2) ได้ว่า
..(3.4)
ในขณะที่สมการ (3.2) นั้นก็สามารถจัดว่าเป็นฟังก์ชันกระตุ้นชนิดหนึ่งด้วยเหมือนกัน เรียกว่าเป็นฟังก์ชันขั้นบันได (阶跃函数, step function)
ลองสร้างฟังก์ชันซิกมอยด์และฟังก์ชันขั้นบันไดขึ้นมาในไพธอน แล้ววาดเทียบกันดู
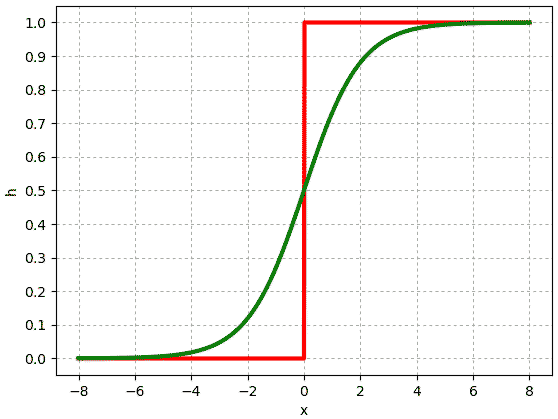
โดยสีเขียวคือฟังก์ชันซิกมอยด์ ส่วนสีแดงคือฟังก์ชันขั้นบันได จะเห็นว่าที่ค่า x มากๆฟังก์ชันซิกมอยด์จะให้ค่าเข้าใกล้ 1 และถ้า x น้อยๆค่าจะเข้าใกล้ 0 ซึ่งจะเหมือนกับฟังก์ชันขั้นบันได
เพียงแต่ถ้าค่า x อยู่ใกล้ 0 ค่าจะอยู่ที่ประมาณ 0.5 ซึ่งอันนี้ต่างจากฟังก์ชันขั้นบันไดมาก
ดังนั้นด้วยการใช้ฟังก์ชันซิกมอยด์ ทำให้เราสามารถได้คำตอบที่หลากหลายขึ้นมาใช้ในการพิจารณา
ฟังก์ชันกระตุ้นนั้นนอกจากซิกมอยด์แล้วก็ยังมีแบบอื่นอีก ซึ่งจะแนะนำต่อไป
ฟังก์ชันค่าเสียหายและการเคลื่อนลงตามความชัน
เพื่อที่จะกำหนดเป้าหมายว่าเราควรจะปรับพารามิเตอร์ในทางใด ในที่นี้จะกำหนดฟังก์ชันตัวนึงขึ้นมา เรียกว่าฟังก์ชันค่าเสียหาย (损失函数, loss function)
ฟังก์ชันค่าเสียหายนี้ถูกกำหนดขึ้นมาเพื่อเป็นตัวบ่งบอกถึงความผิดพลาดของผลการทำนาย กล่าวคือฟังก์ชันค่าเสียหายยิ่งมากยิ่งไม่ดี ดังนั้นเราจึงต้องปรับพารามิเตอร์ไปในทางที่ทำให้ค่านี้ลดลง
ฟังก์ชันค่าเสียหายที่เข้าใจง่ายที่สุดก็คือคำนวณจากผลต่างกำลังสอง
..(3.5)
ซึ่งมาจากแนวคิดง่ายๆว่าถ้าคำตอบจริงต่างจากค่าคำตอบที่ทำนายได้มากเท่าไหร่ก็ยิ่งแสดงว่าผลการทำนายแย่
ผลต่างกำลังสองนิยมใช้ในปัญหาการวิเคราะห์การถดถอย อย่างไรก็ตาม ในปัญหาการจำแนกประเภทข้อมูล ฟังก์ชันค่าเสียหายที่นิยมใช้จริงๆคือ เอนโทรปีไขว้ (交叉熵, cross entropy) คำนวณโดย
..(3.6)
ที่มาของเอนโทรปีไขว้นี้มาจากการพิจารณาค่าความควรจะเป็น (似然函数, likelihood)
ในที่นี้จะไม่อธิบายละเอียด แต่สำหรับคนที่สนใจ มีเขียนอธิบายโดยละเอียดไว้ใน https://phyblas.hinaboshi.com/20161207
สรุปสั้นๆคือเป็นค่าที่แสดงถึงความผิดพลาดในการทำนายความน่าจะเป็น เป็นฟังก์ชันเป้าหมายที่เราต้องการลด ยิ่งมีค่าน้อยก็ยิ่งดี
ต่อมาพิจารณาว่าถ้าปรับค่าพารามิเตอร์ตัวไหนไป ค่าเสียหายจะมีค่าเปลี่ยนแปลงไปยังไง นั่นคือทำการหาอนุพันธ์ย่อย (偏导数, partial derivative) ของ J เทียบกับพารามิเตอร์ตัวนั้น
ค่าอนุพันธ์ในที่นี้มักจะเรียกว่าเป็นค่าความชัน (梯度, gradient)
จะเห็นว่าค่า J ขึ้นอยู่กับ h และ h ขึ้นอยู่กับ a แล้ว a ก็ขึ้นอยู่กับ w และ b อีกที ดังนั้นเราสามารถหาความชันของ J เทียบกับ w ได้ดังนี้
..(3.7)
และอนุพันธ์ย่อยของ J เทียบกับ b เป็นดังนี้
..(3.8)
โดยจากสมการ (3.6) หาอนุพันธ์ได้
..(3.9)
จากสมการ (3.4) ได้
..(3.10)
จากสมการ (3.1) ได้
..(3.11)
..(3.12)
จาก (3.9) และ (3.10) จะได้ว่าความชันของค่าเสียหายเทียบกับ ai เป็น
..(3.13)
ซึ่งจะเห็นว่ามีรูปแบบที่เรียบง่าย แค่นำค่าที่ทำนายได้มาลบกับคำตอบจริง
สุดท้ายจาก (3.11),(3.12),(3.13) แทนลง (3.7) และ (3.8) ก็จะได้ค่าอนุพันธ์ของค่าเสียหายเทียบกับ w และ b
..(3.14)
..(3.15)
เมื่อรู้ว่าพารามิเตอร์แต่ละตัวส่งผลให้ J เปลี่ยนแปลงไปในทางใดแล้ว ที่เหลือก็คือทำการปรับค่าพารามิเตอร์ตัวนั้นไปในทิศทางที่ทำให้ J ลดลง
ค่าน้ำหนัก wj แต่ละตัวปรับได้โดย
..(3.16)
โดย η คืออัตราการเรียนรู้ เช่นเดียวกับในบทที่แล้ว
โดยทั่วไปเราจะพิจารณา w พร้อมกันทั้งอาเรย์ ซึ่งจะได้ว่า
..(3.17)
ส่วนไบแอส b จะปรับโดย
..(3.18)
สุดท้ายสมการที่ใช้ในการปรับก็แทบเหมือนกับตอนใช้อัลกอริธึมอย่างง่าย แต่ต่างตรงที่ ϕ ในครั้งนี้คำนวณด้วยฟังก์ชันซิกมอยด์ แทนที่จะเป็นฟังก์ชันขั้นบันได จึงมีความยืดหยุ่นกว่า
วิธีการที่พิจารณาหาค่าความชันแล้วปรับพารามิเตอร์ไปในทิศทางตามความชันนั้น เรียกว่า การเคลื่อนลงตามความชัน (梯度下降法, gradient descent)
อาจจินตนาการว่าเหมือนเรามีวาดกราฟแสดงความสัมพันธ์ระหว่างตัวแปรต้นกับค่าฟังก์ชันอะไรบางอย่างก็จะเห็นว่าเป็นพื้นผิวโค้งๆ แล้วเราพยายามจะหาจุดต่ำสุดโดยเริ่มจากจุดใดจุดหนึ่ง แล้วเปลี่ยนตำแหน่งไปเรื่อยๆ การย้ายตำแหน่งที่ดีที่สุดก็คือไปตามแนวทางลาด ซึ่งก็คือทิศตรงข้ามกับค่าความชัน แบบนี้ก็จะเป็นการเคลื่อนลง
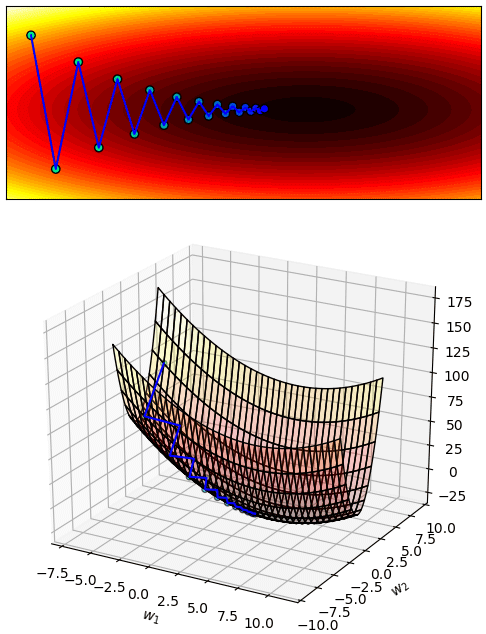
เพียงแต่ว่าในการเคลื่อนที่ครั้งหนึ่งจะเคลื่อนไปเท่าไหร่นั้นก็ขึ้นอยู่กับค่าอัตราการเรียนรู้ (η) ถ้ากำหนดให้สูงเกินไปแทนที่จะเคลื่อนลงเขาก็อาจกลายเป็นโดดข้ามช่องเขาไปมา ไม่ได้ลงร่องสักที
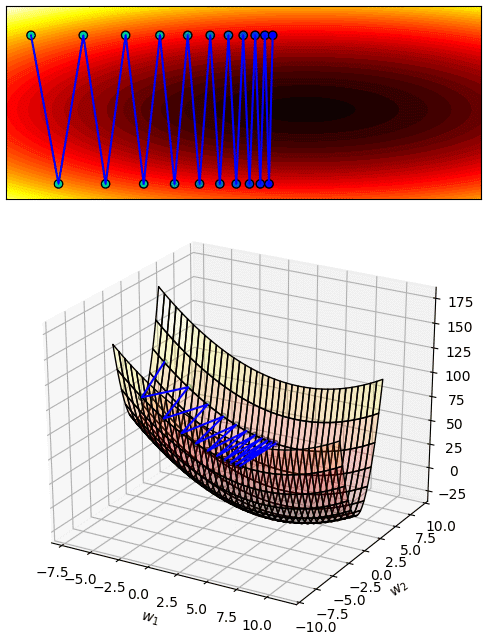
แต่ถ้ากำหนดเล็กเกินไปก็จะเคลื่อนที่ช้ามาก แบบนี้กว่าจะลงไปถึงจุดต่ำสุดก็จะเสียเวลามาก
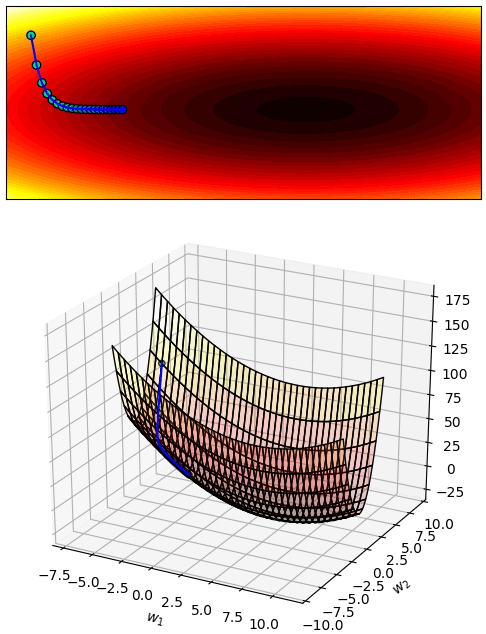
ดังนั้นการกำหนด η ให้เหมาะสมก็เป็นสิ่งที่ต้องพิจารณา ไม่มีคำตอบตายตัวโดยทั่วไป
เกี่ยวกับเรื่องการเคลื่อนลงตามความชันและค่า η ได้เขียนอธิบายละเอียดกว่านี้ไว้ในบทความนี้ แนะนำให้อ่านกัน https://phyblas.hinaboshi.com/20161210
เมื่อจะใช้วิธีการเคลื่อนลงตามความชัน สิ่งสำคัญอย่างหนึ่งก็คือฟังก์ชันกระตุ้นที่ใช้จำเป็นจะต้องเป็นฟังก์ชันต่อเนื่องจึงจะหาอนุพันธ์ของค่าเสียหายได้ แต่ฟังก์ชันขั้นบันไดไม่สามารถหาได้ นี่ก็เป็นเหตุผลหนึ่งที่จำเป็นต้องใช้ฟังก์ชันซิกมอยด์
เทคนิคการจำแนกประเภทข้อมูลโดยใช้เพอร์เซปตรอนที่มีการปรับพารามิเตอร์โดยใช้ฟังก์ชันซิกมอยด์เป็นฟังก์ชันกระตุ้นจะเรียกว่า การวิเคราะห์การถดถอยโลจิสติก (逻辑回归, logistic regression)
ที่จริงแล้วการวิเคราะห์การถดถอยโลจิสติกนั้นมักถูกกล่าวถึงในฐานะเทคนิคการเรียนรู้ของเครื่องเทคนิคนึง แยกออกจากเรื่องของโครงข่ายประสาทเทียม แต่แนวคิดของวิธีนี้ก็ถือเป็นพื้นฐานที่สำคัญที่นำมาใช้ในโครงข่ายประสาทเทียม
อนึ่ง แต่เดิมแล้วในการใช้วิธีการเคลื่อนลงตามความชันเราจะไม่ได้พิจารณาข้อมูลแค่ทีละตัว แต่ใช้ข้อมูลทั้งหมดที่มีพร้อมกัน ดังนั้นค่าเสียหายก็เป็นค่าเฉลี่ยของค่าเสียหายของ x หลายตัวในเวลาเดียวกันแบบนี้
..(3.19)
แบบนี้จะได้ว่าค่าพารามิเตอร์ที่ต้องปรับกลายเป็น
..(3.20)
..(3.21)
ที่เป็นแบบนี้เพราะว่าค่าความเสียหายที่คำนวณได้จากข้อมูลแต่ละตัวไม่เท่ากัน จุดต่ำสุดก็ย่อมไม่เท่ากัน ถ้าในการปรับพารามิเตอร์แต่ละครั้งใช้ค่าคนละตัวกันก็เท่ากับกำลังมุ่งหน้าไปยังจุดต่ำสุดคนละจุด จึงมีความไม่แน่นอน
การคำนวณค่าเสียหายทีละจุดแล้วปรับพารามิเตอร์ทันทีแบบนี้ปกติจะไม่เรียกว่าการเคลื่อนลงตามความชันเฉยๆ แต่จะเรียกว่าการเคลื่อนลงตามความชันแบบสุ่ม (随机梯度下降法, stochastic gradient descent) มักเรียกย่อๆว่า SGD
การทำแบบนี้แม้ว่าจะมีความไม่แน่นอนอยู่บ้างแต่ก็ทำให้การเรียนรู้คืบหน้าไปได้เช่นเดียวกัน เหมือนกับคนที่กำลังเดินลงทางลาดขณะเกิดแผ่นดินไหวทำให้กะความชันได้ไม่แม่นเลยเดินโซเซไปมาอาจมีเบนออกนอกทิศทางหลักไปบ้างแต่ถ้าทิศทางโดยรวมยังแน่นอนอยู่สุดท้ายก็ไปถึงเป้าหมายที่อยู่ด้านล่างได้เหมือนกัน
ข้อดีที่เห็นได้ชัดก็คือคำนวณเร็วกว่า เพราะคำนวณแค่ตัวเดียวก็ปรับค่าเลย ยิ่งถ้าข้อมูลมีจำนวนมากยิ่งเห็นผลชัดเจน
เขียนโปรแกรม
ต่อมาเราจะมาเขียนโค้ดด้วยวิธีใหม่ที่ได้ โดยจะลองทั้งแบบปรับค่าด้วยข้อมูลทีละตัวและปรับค่าด้วยข้อมูลทั้งหมด
เริ่มแรกเพื่อความง่ายจะใช้วิธีการปรับค่าด้วยข้อมูลทีละตัวก่อน
และเพื่อให้เปรียบเทียบกับบทที่แล้ว เราจะใช้ตัวอย่างเดียวกันลองดู นั่นคือเกต AND
เขียนได้แบบนี้
ผลที่ได้จะได้การแบ่งพื้นที่ออกมาอย่างสวยงาม เส้นแบ่งอยู่ค่อนข้างจะตรงกลางระหว่างข้อมูล ๒ ชนิด
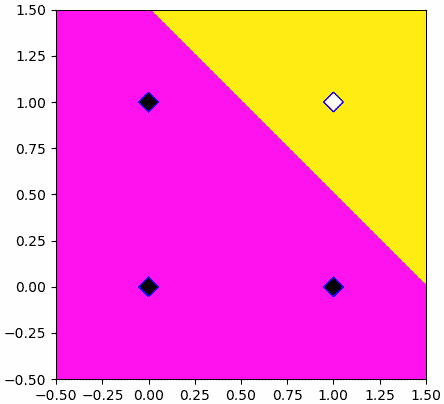
ในที่นี้เรายังคงตัดสินคำตอบในจุดต่างๆโดยดูจากว่าค่าที่คำนวณได้นั้นมากถึง 0 หรือเปล่า จึงแบ่งคำตอบออกเป็นสองเขต เพียงแต่ว่าตอนที่ปรับพารามิเตอร์เปลี่ยนมาใช้คำนวณจากฟังก์ชันกระตุ้นซิกมอยด์แทน
เรายังสามารถนำค่าที่คำนวณจากฟังก์ชันซิกมอยด์มาวาดภาพแสดงการค่าความน่าจะเป็นในแต่ละพื้นที่ได้
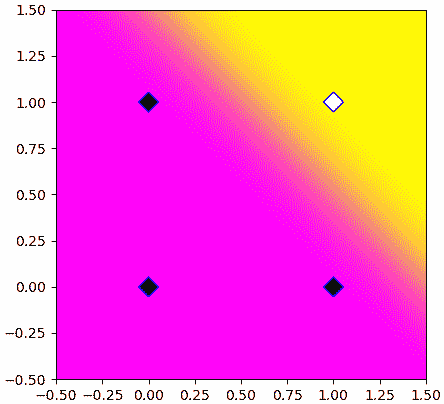
จะเห็นว่าพอใช้ฟังก์ชันซิกมอยด์แล้วเขตแบ่งกลายเป็นค่อยๆเปลี่ยนสีไปทีละนิดแทนที่จะตัดเปลี่ยนไปเลย นี่เป็นความแตกต่างระหว่างฟังก์ชันซิกมอยด์และฟังก์ชันขั้นบันได
สรุปแล้วคือเวลาต้องการหาคำตอบที่แน่ชัดไปเลยเราจะยังคงใช้ฟังก์ชันขั้นบันได แต่เวลาต้องการหาความน่าจะเป็นจะใช้ฟังก์ชันซิกมอยด์
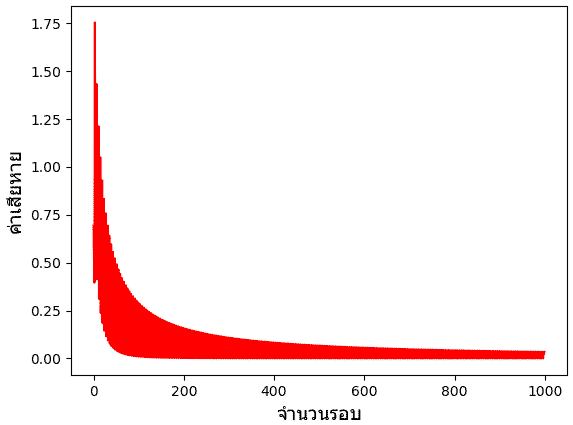
นอกจากนี้ ค่าเอนโทรปีที่คำนวณได้มาขณะเรียนรู้ก็ได้เก็บมาด้วย ในที่นี้ลองเอามาวาดกราฟดู
จะเห็นได้ว่าค่าลดลงเรื่อยๆระหว่างเรียนรู้ เป็นไปตามที่ควรจะเป็น แม้จะมีลักษณะไม่แน่นอนขึ้นๆลงๆ ซึ่งเกิดจากการที่มีการเปลี่ยนเวียนใช้ข้อมูลคนละจุดกันไป
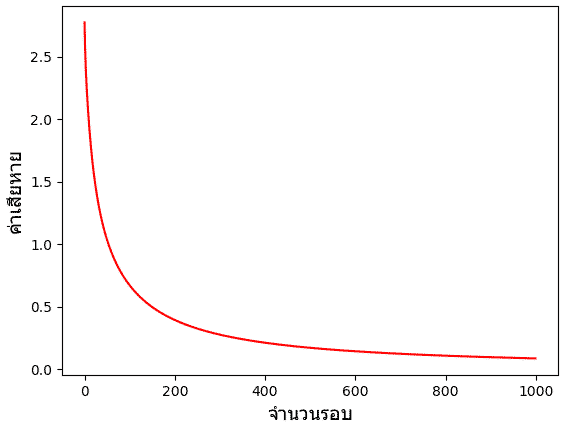
สุดท้าย ลองมาลองอีกวิธีที่คำนวณค่าเสียหายรวมของทุกตัวแล้วจึงนำมาเฉลี่ยแล้วค่อยปรับพารามิเตอร์ทีเดียว
ในที่นี้ผลลัพธ์การแบ่งพื้นที่จะได้ไม่ต่างจากเดิมมากดังนั้นไม่วาดใหม่แล้ว แต่ที่ต่างกันอย่างเห็นได้ชัดก็คือค่าเสียหาย ซึ่งจะเห็นว่าลดลงอย่างสม่ำเสมอ เพราะคราวนี้เราคิดค่าเสียหายจากข้อมูลทั้งหมด จึงมีแนวโน้มลดลงอย่างแน่นอน ค่าลดลงไปเรื่อยๆสู่จุดต่ำสุดอย่างราบรื่น
นอกจากวิธีการที่ใช้ข้อมูลทั้งหมดกับใช้ข้อมูลทีละตัวแล้ว ยังมีวิธีการที่อยู่กึ่งกลางระหว่างนั้น ก็คือการแบ่งข้อมูลเป็นกลุ่มย่อยแล้วใช้ทีละกลุ่ม แบบนี้เรียกว่ามินิแบตช์ (minibatch) ซึ่งเป็นวิธีที่ใช้มากสุดจริงๆในทางปฏิบัติ อย่างไรก็ตามจะยังไม่กล่าวถึงตอนนี้ จะยกไปพูดถึงในบทที่ ๑๕
จนกว่าจะไปถึงบทนั้น เพื่อความสะดวก บทต่อจากนี้ไปเราจะใช้วิธีการปรับค่าพารามิเตอร์โดยพิจารณาค่าเอนโทรปีเฉลี่ยของข้อมูลทุกตัว
>> อ่านต่อ บทที่ ๔
ในบทที่แล้วได้อธิบายหลักการเรียนรู้ปรับปรุงพารามิเตอร์ของเพอร์เซปตรอนอย่างง่ายไปแล้ว
วิธีการปรับพารามิเตอร์อย่างง่ายนั้นยังไม่ดีพอที่จะใช้งานจริง ดังนั้นในบทนี้จะเรียนรู้วิธีการที่นิยมนำมาใช้จริงๆภายในโครงข่ายประสาทเทียมในปัจจุบัน นั่นคือการใช้ฟังก์ชันกระตุ้น (激活函数, activation function)
ฟังก์ชันกระตุ้น
เดิมทีในอัลกอริธีมการปรับพารามิเตอร์ของเพอร์เซปตรอนแบบง่ายนั้นเมื่อนำค่าตัวแปรต้นคูณกับค่าน้ำหนักและบวกไบแอสแล้ว จะทำการทำนายคำตอบให้เป็น 0 หรือ 1 โดยพิจารณาว่าค่าเป็น 0 ขึ้นไปหรือไม่ นั่นคือ
..(3.1)
..(3.2)
โดย h คือค่าที่ทำนายได้ ซึ่งเราจะเอาค่านี้ไปเปรียบเทียบกับคำตอบจริง (z) เพื่อพิจารณาว่าควรปรับพารามิเตอร์เท่าไหร่
แต่ว่าถ้าคำนวณให้ h เป็นแค่ 0 หรือ 1 เท่านั้นแบบนี้ปัญหาคือมันจะไม่ได้บ่งบอกถึงระดับความผิดพลาดในการทำนาย แบบนี้ไม่ว่าค่าจะเกินหรือต่ำกว่าไปแค่ไหนก็จะถูกตัดสินแค่ว่าเป็น 0 หรือ 1 เหมือนกัน
ดังนั้นแทนที่จะตัดสินค่าทำนายเป็น 0 หรือ 1 ไปเลย จึงมีแนวคิดที่จะเปลี่ยนเป็นให้นำ a มาเข้าฟังก์ชันอะไรบางอย่าง เรียกฟังก์ชันนั้นว่าฟังก์ชันกระตุ้น
ฟังก์ชันกระตุ้นอาจเป็นอะไรก็ได้ที่มีลักษณะเป็นฟังก์ชันเพิ่ม (คือมีค่ามากเมื่อ x มาก และน้อยเมื่อ x น้อย x ที่ค่ามากกว่าจะต้องได้ค่าฟังก์ชันที่มากกว่าหรือเท่ากับค่า x ที่น้อยกว่าเสมอ)
ในการวิเคราะห์จำแนกประเภท ๒ กลุ่ม ฟังก์ชันกระตุ้นที่นิยมที่สุดคือฟังก์ชันซิกมอยด์ (sigmoid) นิยามดังนี้
..(3.3)
เมื่อนำฟังก์ชันนี้มาใช้เป็นฟังก์ชันกระตุ้นก็จะเขียนแทนสมการ (3.2) ได้ว่า
..(3.4)
ในขณะที่สมการ (3.2) นั้นก็สามารถจัดว่าเป็นฟังก์ชันกระตุ้นชนิดหนึ่งด้วยเหมือนกัน เรียกว่าเป็นฟังก์ชันขั้นบันได (阶跃函数, step function)
ลองสร้างฟังก์ชันซิกมอยด์และฟังก์ชันขั้นบันไดขึ้นมาในไพธอน แล้ววาดเทียบกันดู
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
def bandai(x):
return x>0
x = np.linspace(-8,8,1001)
plt.axes(yticks=np.linspace(0,1,11),xlabel='x',ylabel='h')
plt.plot(x,bandai(x),'r',lw=3)
plt.plot(x,sigmoid(x),'g',lw=3)
plt.grid(ls=':')
plt.show()
โดยสีเขียวคือฟังก์ชันซิกมอยด์ ส่วนสีแดงคือฟังก์ชันขั้นบันได จะเห็นว่าที่ค่า x มากๆฟังก์ชันซิกมอยด์จะให้ค่าเข้าใกล้ 1 และถ้า x น้อยๆค่าจะเข้าใกล้ 0 ซึ่งจะเหมือนกับฟังก์ชันขั้นบันได
เพียงแต่ถ้าค่า x อยู่ใกล้ 0 ค่าจะอยู่ที่ประมาณ 0.5 ซึ่งอันนี้ต่างจากฟังก์ชันขั้นบันไดมาก
ดังนั้นด้วยการใช้ฟังก์ชันซิกมอยด์ ทำให้เราสามารถได้คำตอบที่หลากหลายขึ้นมาใช้ในการพิจารณา
ฟังก์ชันกระตุ้นนั้นนอกจากซิกมอยด์แล้วก็ยังมีแบบอื่นอีก ซึ่งจะแนะนำต่อไป
ฟังก์ชันค่าเสียหายและการเคลื่อนลงตามความชัน
เพื่อที่จะกำหนดเป้าหมายว่าเราควรจะปรับพารามิเตอร์ในทางใด ในที่นี้จะกำหนดฟังก์ชันตัวนึงขึ้นมา เรียกว่าฟังก์ชันค่าเสียหาย (损失函数, loss function)
ฟังก์ชันค่าเสียหายนี้ถูกกำหนดขึ้นมาเพื่อเป็นตัวบ่งบอกถึงความผิดพลาดของผลการทำนาย กล่าวคือฟังก์ชันค่าเสียหายยิ่งมากยิ่งไม่ดี ดังนั้นเราจึงต้องปรับพารามิเตอร์ไปในทางที่ทำให้ค่านี้ลดลง
ฟังก์ชันค่าเสียหายที่เข้าใจง่ายที่สุดก็คือคำนวณจากผลต่างกำลังสอง
..(3.5)
ซึ่งมาจากแนวคิดง่ายๆว่าถ้าคำตอบจริงต่างจากค่าคำตอบที่ทำนายได้มากเท่าไหร่ก็ยิ่งแสดงว่าผลการทำนายแย่
ผลต่างกำลังสองนิยมใช้ในปัญหาการวิเคราะห์การถดถอย อย่างไรก็ตาม ในปัญหาการจำแนกประเภทข้อมูล ฟังก์ชันค่าเสียหายที่นิยมใช้จริงๆคือ เอนโทรปีไขว้ (交叉熵, cross entropy) คำนวณโดย
..(3.6)
ที่มาของเอนโทรปีไขว้นี้มาจากการพิจารณาค่าความควรจะเป็น (似然函数, likelihood)
ในที่นี้จะไม่อธิบายละเอียด แต่สำหรับคนที่สนใจ มีเขียนอธิบายโดยละเอียดไว้ใน https://phyblas.hinaboshi.com/20161207
สรุปสั้นๆคือเป็นค่าที่แสดงถึงความผิดพลาดในการทำนายความน่าจะเป็น เป็นฟังก์ชันเป้าหมายที่เราต้องการลด ยิ่งมีค่าน้อยก็ยิ่งดี
ต่อมาพิจารณาว่าถ้าปรับค่าพารามิเตอร์ตัวไหนไป ค่าเสียหายจะมีค่าเปลี่ยนแปลงไปยังไง นั่นคือทำการหาอนุพันธ์ย่อย (偏导数, partial derivative) ของ J เทียบกับพารามิเตอร์ตัวนั้น
ค่าอนุพันธ์ในที่นี้มักจะเรียกว่าเป็นค่าความชัน (梯度, gradient)
จะเห็นว่าค่า J ขึ้นอยู่กับ h และ h ขึ้นอยู่กับ a แล้ว a ก็ขึ้นอยู่กับ w และ b อีกที ดังนั้นเราสามารถหาความชันของ J เทียบกับ w ได้ดังนี้
..(3.7)
และอนุพันธ์ย่อยของ J เทียบกับ b เป็นดังนี้
..(3.8)
โดยจากสมการ (3.6) หาอนุพันธ์ได้
..(3.9)
จากสมการ (3.4) ได้
..(3.10)
จากสมการ (3.1) ได้
..(3.11)
..(3.12)
จาก (3.9) และ (3.10) จะได้ว่าความชันของค่าเสียหายเทียบกับ ai เป็น
..(3.13)
ซึ่งจะเห็นว่ามีรูปแบบที่เรียบง่าย แค่นำค่าที่ทำนายได้มาลบกับคำตอบจริง
สุดท้ายจาก (3.11),(3.12),(3.13) แทนลง (3.7) และ (3.8) ก็จะได้ค่าอนุพันธ์ของค่าเสียหายเทียบกับ w และ b
..(3.14)
..(3.15)
เมื่อรู้ว่าพารามิเตอร์แต่ละตัวส่งผลให้ J เปลี่ยนแปลงไปในทางใดแล้ว ที่เหลือก็คือทำการปรับค่าพารามิเตอร์ตัวนั้นไปในทิศทางที่ทำให้ J ลดลง
ค่าน้ำหนัก wj แต่ละตัวปรับได้โดย
..(3.16)
โดย η คืออัตราการเรียนรู้ เช่นเดียวกับในบทที่แล้ว
โดยทั่วไปเราจะพิจารณา w พร้อมกันทั้งอาเรย์ ซึ่งจะได้ว่า
..(3.17)
ส่วนไบแอส b จะปรับโดย
..(3.18)
สุดท้ายสมการที่ใช้ในการปรับก็แทบเหมือนกับตอนใช้อัลกอริธึมอย่างง่าย แต่ต่างตรงที่ ϕ ในครั้งนี้คำนวณด้วยฟังก์ชันซิกมอยด์ แทนที่จะเป็นฟังก์ชันขั้นบันได จึงมีความยืดหยุ่นกว่า
วิธีการที่พิจารณาหาค่าความชันแล้วปรับพารามิเตอร์ไปในทิศทางตามความชันนั้น เรียกว่า การเคลื่อนลงตามความชัน (梯度下降法, gradient descent)
อาจจินตนาการว่าเหมือนเรามีวาดกราฟแสดงความสัมพันธ์ระหว่างตัวแปรต้นกับค่าฟังก์ชันอะไรบางอย่างก็จะเห็นว่าเป็นพื้นผิวโค้งๆ แล้วเราพยายามจะหาจุดต่ำสุดโดยเริ่มจากจุดใดจุดหนึ่ง แล้วเปลี่ยนตำแหน่งไปเรื่อยๆ การย้ายตำแหน่งที่ดีที่สุดก็คือไปตามแนวทางลาด ซึ่งก็คือทิศตรงข้ามกับค่าความชัน แบบนี้ก็จะเป็นการเคลื่อนลง

เพียงแต่ว่าในการเคลื่อนที่ครั้งหนึ่งจะเคลื่อนไปเท่าไหร่นั้นก็ขึ้นอยู่กับค่าอัตราการเรียนรู้ (η) ถ้ากำหนดให้สูงเกินไปแทนที่จะเคลื่อนลงเขาก็อาจกลายเป็นโดดข้ามช่องเขาไปมา ไม่ได้ลงร่องสักที

แต่ถ้ากำหนดเล็กเกินไปก็จะเคลื่อนที่ช้ามาก แบบนี้กว่าจะลงไปถึงจุดต่ำสุดก็จะเสียเวลามาก

ดังนั้นการกำหนด η ให้เหมาะสมก็เป็นสิ่งที่ต้องพิจารณา ไม่มีคำตอบตายตัวโดยทั่วไป
เกี่ยวกับเรื่องการเคลื่อนลงตามความชันและค่า η ได้เขียนอธิบายละเอียดกว่านี้ไว้ในบทความนี้ แนะนำให้อ่านกัน https://phyblas.hinaboshi.com/20161210
เมื่อจะใช้วิธีการเคลื่อนลงตามความชัน สิ่งสำคัญอย่างหนึ่งก็คือฟังก์ชันกระตุ้นที่ใช้จำเป็นจะต้องเป็นฟังก์ชันต่อเนื่องจึงจะหาอนุพันธ์ของค่าเสียหายได้ แต่ฟังก์ชันขั้นบันไดไม่สามารถหาได้ นี่ก็เป็นเหตุผลหนึ่งที่จำเป็นต้องใช้ฟังก์ชันซิกมอยด์
เทคนิคการจำแนกประเภทข้อมูลโดยใช้เพอร์เซปตรอนที่มีการปรับพารามิเตอร์โดยใช้ฟังก์ชันซิกมอยด์เป็นฟังก์ชันกระตุ้นจะเรียกว่า การวิเคราะห์การถดถอยโลจิสติก (逻辑回归, logistic regression)
ที่จริงแล้วการวิเคราะห์การถดถอยโลจิสติกนั้นมักถูกกล่าวถึงในฐานะเทคนิคการเรียนรู้ของเครื่องเทคนิคนึง แยกออกจากเรื่องของโครงข่ายประสาทเทียม แต่แนวคิดของวิธีนี้ก็ถือเป็นพื้นฐานที่สำคัญที่นำมาใช้ในโครงข่ายประสาทเทียม
อนึ่ง แต่เดิมแล้วในการใช้วิธีการเคลื่อนลงตามความชันเราจะไม่ได้พิจารณาข้อมูลแค่ทีละตัว แต่ใช้ข้อมูลทั้งหมดที่มีพร้อมกัน ดังนั้นค่าเสียหายก็เป็นค่าเฉลี่ยของค่าเสียหายของ x หลายตัวในเวลาเดียวกันแบบนี้
..(3.19)
แบบนี้จะได้ว่าค่าพารามิเตอร์ที่ต้องปรับกลายเป็น
..(3.20)
..(3.21)
ที่เป็นแบบนี้เพราะว่าค่าความเสียหายที่คำนวณได้จากข้อมูลแต่ละตัวไม่เท่ากัน จุดต่ำสุดก็ย่อมไม่เท่ากัน ถ้าในการปรับพารามิเตอร์แต่ละครั้งใช้ค่าคนละตัวกันก็เท่ากับกำลังมุ่งหน้าไปยังจุดต่ำสุดคนละจุด จึงมีความไม่แน่นอน
การคำนวณค่าเสียหายทีละจุดแล้วปรับพารามิเตอร์ทันทีแบบนี้ปกติจะไม่เรียกว่าการเคลื่อนลงตามความชันเฉยๆ แต่จะเรียกว่าการเคลื่อนลงตามความชันแบบสุ่ม (随机梯度下降法, stochastic gradient descent) มักเรียกย่อๆว่า SGD
การทำแบบนี้แม้ว่าจะมีความไม่แน่นอนอยู่บ้างแต่ก็ทำให้การเรียนรู้คืบหน้าไปได้เช่นเดียวกัน เหมือนกับคนที่กำลังเดินลงทางลาดขณะเกิดแผ่นดินไหวทำให้กะความชันได้ไม่แม่นเลยเดินโซเซไปมาอาจมีเบนออกนอกทิศทางหลักไปบ้างแต่ถ้าทิศทางโดยรวมยังแน่นอนอยู่สุดท้ายก็ไปถึงเป้าหมายที่อยู่ด้านล่างได้เหมือนกัน
ข้อดีที่เห็นได้ชัดก็คือคำนวณเร็วกว่า เพราะคำนวณแค่ตัวเดียวก็ปรับค่าเลย ยิ่งถ้าข้อมูลมีจำนวนมากยิ่งเห็นผลชัดเจน
เขียนโปรแกรม
ต่อมาเราจะมาเขียนโค้ดด้วยวิธีใหม่ที่ได้ โดยจะลองทั้งแบบปรับค่าด้วยข้อมูลทีละตัวและปรับค่าด้วยข้อมูลทั้งหมด
เริ่มแรกเพื่อความง่ายจะใช้วิธีการปรับค่าด้วยข้อมูลทีละตัวก่อน
และเพื่อให้เปรียบเทียบกับบทที่แล้ว เราจะใช้ตัวอย่างเดียวกันลองดู นั่นคือเกต AND
เขียนได้แบบนี้
def sigmoid(x):
return 1/(1+np.exp(-x))
def ha_entropy(z,h):
return -(z*np.log(h)+(1-z)*np.log(1-h))
# คำตอบของเกต AND
X = np.array([
[0,0],
[0,1],
[1,0],
[1,1]
])
z = np.array([0,0,0,1])
w = np.array([0,0.]) # พารามิเตอร์ตั้งต้น
b = 0
n = len(z) # จำนวนข้อมูล
eta = 0.8 # อัตราการเรียนรู้
thamsam = 250
entropy = []
for o in range(thamsam):
for i in range(n):
ai = np.dot(X[i],w) + b
hi = sigmoid(ai)
gai = hi-z[i]
gwi = gai*X[i]
gbi = gai
w -= eta*gwi # ปรับค่าพารามิเตอร์
b -= eta*gbi
J = ha_entropy(z[i],hi) # คำนวณค่าเสียหายเก็บไว้
entropy.append(J)
# วาดแสดงการแบ่งพื้นที่
mx,my = np.meshgrid(np.linspace(-0.5,1.5,200),np.linspace(-0.5,1.5,200))
mX = np.array([mx.ravel(),my.ravel()]).T
mh = np.dot(mX,w) + b
mz = (mh>=0).astype(int).reshape(200,-1)
plt.axes(aspect=1)
plt.contourf(mx,my,mz,cmap='spring')
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='b',marker='D',cmap='gray')
plt.show()ผลที่ได้จะได้การแบ่งพื้นที่ออกมาอย่างสวยงาม เส้นแบ่งอยู่ค่อนข้างจะตรงกลางระหว่างข้อมูล ๒ ชนิด

ในที่นี้เรายังคงตัดสินคำตอบในจุดต่างๆโดยดูจากว่าค่าที่คำนวณได้นั้นมากถึง 0 หรือเปล่า จึงแบ่งคำตอบออกเป็นสองเขต เพียงแต่ว่าตอนที่ปรับพารามิเตอร์เปลี่ยนมาใช้คำนวณจากฟังก์ชันกระตุ้นซิกมอยด์แทน
เรายังสามารถนำค่าที่คำนวณจากฟังก์ชันซิกมอยด์มาวาดภาพแสดงการค่าความน่าจะเป็นในแต่ละพื้นที่ได้
mz = sigmoid(mh).reshape(200,-1)
plt.axes(aspect=1)
plt.contourf(mx,my,mz,50,cmap='spring')
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='b',marker='D',cmap='gray')
plt.show()
จะเห็นว่าพอใช้ฟังก์ชันซิกมอยด์แล้วเขตแบ่งกลายเป็นค่อยๆเปลี่ยนสีไปทีละนิดแทนที่จะตัดเปลี่ยนไปเลย นี่เป็นความแตกต่างระหว่างฟังก์ชันซิกมอยด์และฟังก์ชันขั้นบันได
สรุปแล้วคือเวลาต้องการหาคำตอบที่แน่ชัดไปเลยเราจะยังคงใช้ฟังก์ชันขั้นบันได แต่เวลาต้องการหาความน่าจะเป็นจะใช้ฟังก์ชันซิกมอยด์
นอกจากนี้ ค่าเอนโทรปีที่คำนวณได้มาขณะเรียนรู้ก็ได้เก็บมาด้วย ในที่นี้ลองเอามาวาดกราฟดู
plt.plot(entropy,'r')
plt.xlabel(u'จำนวนรอบ',family='tahoma',size=14)
plt.ylabel(u'ค่าเสียหาย',family='tahoma',size=14)
plt.show()จะเห็นได้ว่าค่าลดลงเรื่อยๆระหว่างเรียนรู้ เป็นไปตามที่ควรจะเป็น แม้จะมีลักษณะไม่แน่นอนขึ้นๆลงๆ ซึ่งเกิดจากการที่มีการเปลี่ยนเวียนใช้ข้อมูลคนละจุดกันไป

สุดท้าย ลองมาลองอีกวิธีที่คำนวณค่าเสียหายรวมของทุกตัวแล้วจึงนำมาเฉลี่ยแล้วค่อยปรับพารามิเตอร์ทีเดียว
w = np.array([0,0.])
b = 0
eta = 0.8
thamsam = 1000
entropy = []
for o in range(thamsam):
dw = 0
db = 0
J = 0
for i in range(n):
ai = np.dot(X[i],w) + b
hi = sigmoid(ai)
gai = hi-z[i]
gwi = gai*X[i]
gbi = gai
dw -= eta*gwi
db -= eta*gbi
J += ha_entropy(z[i],hi)
w += dw/n
b += db/n
entropy.append(J)
plt.figure()
plt.plot(entropy,'r')
plt.xlabel(u'จำนวนรอบ',family='tahoma',size=14)
plt.ylabel(u'ค่าเสียหาย',family='tahoma',size=14)
plt.show()ในที่นี้ผลลัพธ์การแบ่งพื้นที่จะได้ไม่ต่างจากเดิมมากดังนั้นไม่วาดใหม่แล้ว แต่ที่ต่างกันอย่างเห็นได้ชัดก็คือค่าเสียหาย ซึ่งจะเห็นว่าลดลงอย่างสม่ำเสมอ เพราะคราวนี้เราคิดค่าเสียหายจากข้อมูลทั้งหมด จึงมีแนวโน้มลดลงอย่างแน่นอน ค่าลดลงไปเรื่อยๆสู่จุดต่ำสุดอย่างราบรื่น

นอกจากวิธีการที่ใช้ข้อมูลทั้งหมดกับใช้ข้อมูลทีละตัวแล้ว ยังมีวิธีการที่อยู่กึ่งกลางระหว่างนั้น ก็คือการแบ่งข้อมูลเป็นกลุ่มย่อยแล้วใช้ทีละกลุ่ม แบบนี้เรียกว่ามินิแบตช์ (minibatch) ซึ่งเป็นวิธีที่ใช้มากสุดจริงๆในทางปฏิบัติ อย่างไรก็ตามจะยังไม่กล่าวถึงตอนนี้ จะยกไปพูดถึงในบทที่ ๑๕
จนกว่าจะไปถึงบทนั้น เพื่อความสะดวก บทต่อจากนี้ไปเราจะใช้วิธีการปรับค่าพารามิเตอร์โดยพิจารณาค่าเอนโทรปีเฉลี่ยของข้อมูลทุกตัว
>> อ่านต่อ บทที่ ๔
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy