ต่อจาก บทที่ ๒๐

หลังจากที่บทที่แล้วได้เริ่มแนะนำโครงข่ายประสาทแบบคอนโวลูชัน (CNN) หนึ่งมิติไปแล้ว บทนี้จะเป็นเรื่องของโ่ครงข่ายประสาทแบบคอนโวลูชันสองมิติ ซึ่งก็จะมีความซับซ้อนขึ้นไปอีกขั้นหนึ่ง




ว่าด้วยเรื่องข้อมูลรูปภาพ

ข้อมูลรูปภาพ เป็นข้อมูลสองมิติที่มักถูกนำมาวิเคราะห์ด้วยโครงข่ายประสาทแบบคอนโวลูชัน

ในบทนี้จะใช้ข้อมูลตัวอย่างเป็นรูปภาพ อย่างที่ใช้มาตั้งแต่บทที่ ๔

ข้อมูลสามารถโหลดได้จาก >> ruprang-raisi-25x25x1000x5.rar

เมื่อโหลดแล้วลองเปิดภาพขึ้นมาดู จะเห็นว่าแต่ละภาพเป็นภาพขาวดำขนาด 25×25 พิกเซล

ลองเอารูปหนึ่งในนั้นมาวาดแสดงโดย matplotlib

import numpy as np
import matplotlib.pyplot as plt

X = plt.imread('ruprang-raisi-25x25x1000x5/4/00112.png')
plt.figure(figsize=[6.5,5.7],dpi=100)
tick = np.arange(1,26)
plt.xticks(tick-0.5,tick)
plt.yticks(tick-0.5,tick)
plt.xlabel('ตำแหน่งในมิติ 1 ($t_1$)',family='Tahoma',size=14)
plt.ylabel('ตำแหน่งในมิติ 2 ($t_2$)',family='Tahoma',size=14)
plt.imshow(X,cmap='gray')
plt.colorbar(pad=0.01,aspect=50)
plt.grid(ls='--')
plt.tight_layout()
plt.show()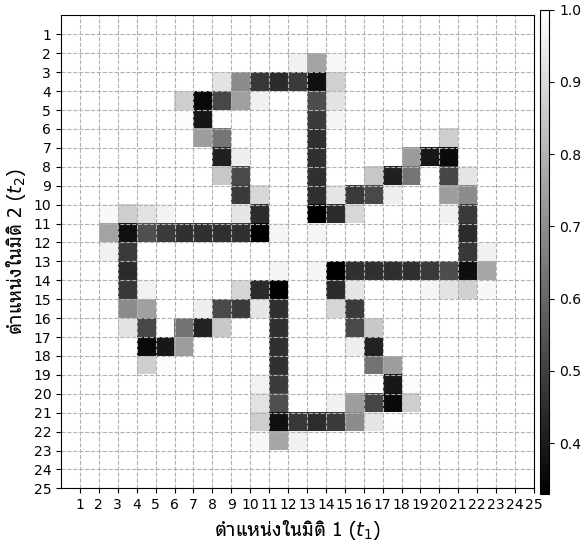

ในที่นี้ข้อมูลมีสองมิติ ให้ตำแหน่งในทั้งสองมิตินี้เป็น $t_1$ และ $t_2$ ในตัวอย่างนี้ข้อมูล 25×25 ก็คือมี $t_1=1,2,⋯,25$ และ $t_2=1,2,\cdots,25$

นอกจากนี้ในบทนี้จะใช้ข้อมูลภาพสีด้วย ซึ่งก็สามารถโหลดได้จาก >> ruprang-misi-25x25x1000x6.rar

ภาพสีประกอบไปด้วยข้อมูลสามสี RGB (แดง,เขียว,น้ำเงิน) ซึ่งถ้านำมาใส่ในโครงข่ายประสาทแบบคอนโวลูชันก็เท่ากับเป็นข้อมูล 3 ช่อง ในขณะที่ข้อมูลภาพขาวดำจะมีแค่ 1 ช่อง

ลองเอารูปหนึ่งในนั้นมาวาดแสดงแยกส่วนประกอบแต่ละสีโดย matplotlib ดู

X = plt.imread('ruprang-misi-25x25x1000x6/4/00005.png')
X = X[:,:,:3]
plt.figure(figsize=[6.5,6.5],dpi=100)
tick = np.arange(1,26)
plt.subplot(2,2,1,xticks=tick-0.5,yticks=tick-0.5,xticklabels=[],yticklabels=[])
plt.title('ภาพเดิม',family='Tahoma',size=13)
plt.imshow(X)
plt.grid(ls='--')

for i in range(3):
    plt.subplot(2,2,2+i,xticks=tick-0.5,yticks=tick-0.5,xticklabels=[],yticklabels=[])
    plt.title(['ส่วน R (ช่อง 1)','ส่วน G (ช่อง 2)','ส่วน B (ช่อง 3)'][i],family='Tahoma',size=13)
    X_ = np.zeros_like(X)
    X_[:,:,i] = X[:,:,i]
    plt.imshow(X_)
    plt.grid(ls='--')
    
plt.tight_layout()
plt.show()

ภาพเหล่านี้จะนำมาใช้เป็นตัวอย่างให้วิเคราะห์จำแนกโดยใช้โครงข่ายประสาทเทียมสองมิติ




โครงสร้างของโครงข่ายประสาทแบบคอนโวลูชันสองมิติ

โครงสร้างของโครงข่ายประสาทแบบคอนโวลูชันสองมิติก็จะมีลักษณะเดียวกับกรณีหนึ่งมิติ แค่ชั้นคำนวณคอนโวลูชันและชั้นบ่อรวมสูงสุดจะใช้เป็นแบบสองมิติ



โครงสร้างจะเริ่มจากส่วนของชั้นคอนโวลูชัน เสร็จแล้วก็จะไปสู่ส่วนของชั้นเชิงเส้น โดยที่เมื่อเปลี่ยนจากชั้นคอนโวลูชันไปชั้นเชิงเส้นจะต้องมีการเปลี่ยนรูป โดย

$\;\;\;จำนวนเซลล์เข้าชั้นเชิงเส้น = \begin{align} จำนวนช่องขาออกจากชั้นคอนโวลูชัน\\×\\ความสูงตัวกรอง\\×\\ความกว้างตัวกรอง\end{align}$

สมมุติว่ามีตัวกรองอยู่ 2 ตัว ขนาดสูง 3 กว้าง 4 ก็จะกลายเป็น 2×3×4=24 เซลล์ ดังในภาพนี้






สหสัมพันธ์ไขว้และคอนโวลูชันในสองมิติ

เช่นเดียวกับที่อธิบายคอนโวลูชันหนึ่งมิติไปในบทที่แล้ว การคำนวณที่เกิดขึ้นในชั้นคอนโวลูชันสองมิติก็คือสหสัมพันธ์ไขว้สองมิติ

การคำนวณภายในตัวกรองแต่ละตัวนั้นอาจแสดงเป็นภาพเคลื่อนไหวได้ดังนี้



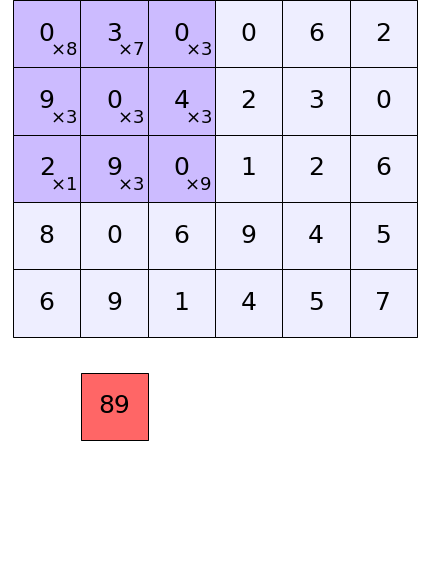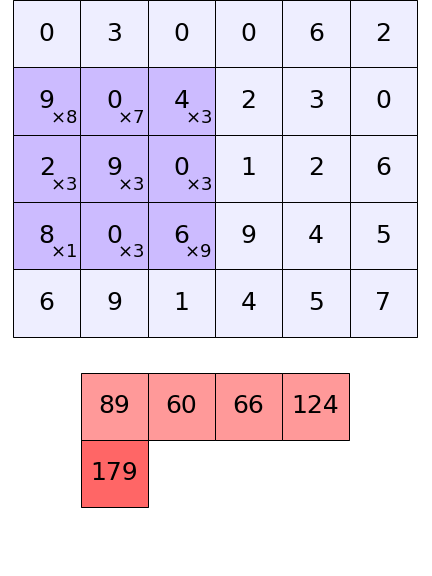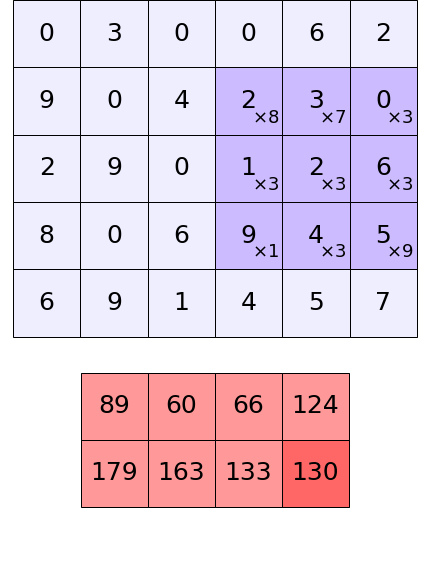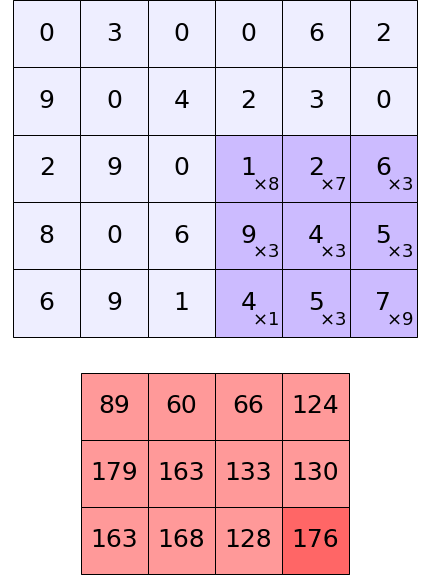
สำหรับการคำนวณจริงๆที่เกิดขึ้นในโครงข่ายประสาทแบบคอนโวลูชันนั้นตัวกรองหลายตัวจะถูกใช้เพื่อคำนวณไปพร้อมๆกัน และยังมีการบวกกับค่าไบแอสด้วย ซึ่งจะซับซ้อนขึ้นไปยิ่งกว่าในภาพนี้




การคำนวณภายในชั้นคอนโวลูชันสองมิติ

ต่อมาพูดถึงการคำนวณที่เกิดขึ้นภายในชั้นคอนโวลูชันสองมิติ

สมมุติว่าชั้นที่ 1 กับ 2 เป็นชั้นคอนโวลูชันสองมิติ ดังที่วาดในภาพแสดงโครงสร้างด้านบน การคำนวณที่เกิดขึ้นภายในนั้นจะเป็นดังนี้

$\begin{align} a_1^{(ι,j,t_1,t_2)} &= \sum_{i=1}^{c_0} \sum_{μ_1=1}^{k_{1,1}} \sum_{μ_2=1}^{k_{1,2}} w_1^{(i,j,μ_1,μ_2)}x^{(ι,i,s_{1,1}(t_1-1)+μ_1,s_{1,2}(t_2-1)+μ_2)} + b_1^{(j)} \end{align}$ ..(21.1)

$\begin{align} a_2^{(ι,j,t_1,t_2)} &= \sum_{i=1}^{c_1} \sum_{μ_1=1}^{k_{2,1}} \sum_{μ_2=1}^{k_{2,2}} w_2^{(i,j,μ_1,μ_2)}h_1^{(ι,i,s_{2,1}(t_1-1)+μ_1,s_{2,2}(t_2-1)+μ_2)} + b_2^{(j)} \end{align}$ ..(21.2)

ให้ลองเทียบกับสมการ (20.11) กับ (20.12) ในบทที่ ๒๐ จะเห็นว่าคล้ายกันแต่เพิ่มความซับซ้อนขึ้นมา

ในที่นี้ $c_0$ และ $c_1$ คือจำนวนข้อมูลขาเข้าและขาออกของชั้นที่ 1 เช่นเดียวกับในกรณีหนึ่งมิติ

กรณีภาพขาวดำ ข้อมูลขาเข้าในชั้นแรกสุดจะมีแค่ค่าเดียว ดังนั้น $c_0=1$ แต่หากเป็นภาพสี จะเป็นข้อมูล RGB (แดง,เขียว,น้ำเงิน) ดังนั้น $c_0=3$

แต่เมื่อเป็นสองมิติ ตัวกรองก็จะมีสองมิติคือ $k_{1,1}k_{1,2}$ เป็นความสูงและความกว้างของตัวกรองชั้นที่ 1 และ $k_{2,1}k_{2,2}$ เป็นความสูงและความกว้างของตัวกรองชั้นที่ 2

ส่วนดัชนีที่อยู่ในวงเล็บด้านบนมี $ι,i,j,t_1,t_2,μ_1,μ_2$

$ι$ คือดัชนีบอกว่าเป็นข้อมูลตัวที่เท่าไหร่

$i$ คือดัชนีบอกลำดับช่องของข้อมูลขาเข้าของชั้นนั้น

$j$ คือดัชนีบอกลำดับช่องของข้อมูลขาออกของชั้นนั้น

$t_1,t_2$ คือดัชนีบอกตำแหน่งข้อมูลตามแนวความสูงและความกว้าง

ถ้าหาก x เป็นค่าในข้อมูลรูปภาพสี จะได้ว่า $x^{(ι,i,t_1,t_2)}$ คือข้อมูลของภาพที่ $ι$ ในสีที่ $i$ (โดย $i=1$ แดง, $i=2$ เขียว, $i=3$ น้ำเงิน) ในตำแหน่ง $(t_1,t_2)$

และ $μ_1,μ_2$ เป็นดัชนีบอกตำแหน่งภายในตัวกรองตามแนวความสูงและความกว้าง

$w_1,w_2$ คือพารามิเตอร์น้ำหนักในตัวกรอง ซึ่งจำนวนพารามิเตอร์นี้จะมีเท่ากับ

$\begin{align}จำนวนช่องของข้อมูลขาเข้า\\×\\จำนวนช่องของข้อมูลขาออก\\×\\ความสูงตัวกรอง\\×\\ความกว้างตัวกรอง\end{align}$

เช่น $w_1$ มีจำนวนเท่ากับ $c_0×c_1×k_{1,1}×k_{1,2}$ และ $w_2$ มีจำนวนเท่ากับ $c_1×c_2×k_{2,1}×k_{2,2}$

ส่วนพารามิเตอร์ค่าไบแอส $b_1,b_2$ นั้นจะมีแค่จำนวนเท่ากับจำนวนช่องขาออก

ความสัมพันธ์ระหว่างขนาดข้อมูลขาเข้าและขาออกเป็นดังนี้

$\begin{align} ความสูงข้อมูลขาออก = \frac{ความสูงข้อมูลขาเข้า−ความสูงตัวกรอง+จำนวนขอบที่เติมบนล่าง×2}{ความกว้างที่เลื่อนในแต่ละครั้ง} \\ ความกว้างข้อมูลขาออก = \frac{ความกว้างข้อมูลขาเข้า−ความกว้างตัวกรอง+จำนวนขอบที่เติมซ้ายขวา×2}{ความสูงที่เลื่อนในแต่ละครั้ง} \\ \end{align}$ ..(21.3)

ซึ่งเหมือนกับสมการ (20.13) ในบทที่แล้ว แค่ต้องคิดพิจารณาทั้งสองมิติ ตามแนวความสูงและความกว้างแยกกัน

สำหรับภาพแสดงการคำนวณที่เกิดขึ้นภายในชั้นนั้นได้ทำเอาไว้เป็นคลิปลงใน facebook ไว้ ให้เข้าไปดูวีดีโอตัวอย่างในลิงก์นี้ >> https://www.facebook.com/watch/?v=904503580382726

เนื่องจากมีขนาดใหญ่ ในที่นี้จะขอลงเฉพาะภาพสุดท้ายซึ่งเป็นผลลัพธ์ตอนท้ายสุดของการคำนวณ แสดงดังภาพนี้ ส่วนภาพเคลื่อนไหวแสดงรายละเอียดขั้นตอนการคำนวณในแต่ละขั้นจะแสดงในคลิป



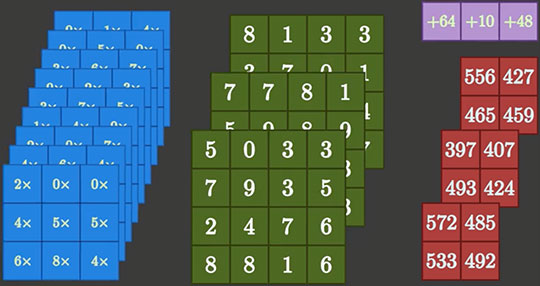
ในภาพนี้เป็นกรณีที่ข้อมูลขาเข้ามี ความสูง×ความกว้าง เป็น 4×4 และ $\begin{align}c_0 = 3,c_1 = 3,k_{1,1} = 3,k_{1,2} = 3\end{align}$

ซึ่งจะได้ข้อมูลขาออกเป็นขนาด 2×2

ช่องสีเขียวในภาพคือข้อมูลขาเข้า

ช่องสีน้ำเงินทางซ้ายที่เอามาวิ่งไล่คูณกับข้อมูลขาเข้าก็คือพารามิเตอร์น้ำหนักบนตัวกรอง ซึ่งมีทั้งหมด 3×3×3×3=27 ตัว

ช่องสีม่วงที่มุมบนขวาคือค่าพารามิเตอร์ไบแอสมี 3 ตัว เท่ากับจำนวนช่องขาออก

เมื่อคูณน้ำหนักบนตัวกรองและบวกด้วยไบแอสแล้ว ผลลัพธ์ที่ได้ก็คือข้อมูลขาออก คือช่องสีแดงทางขวาของภาพ




การเขียนคลาสของชั้นคอนโวลูชันสองมิติ

เมื่อเข้าใจหลักการคำนวณที่เกิดขึ้นแล้ว ต่อมาก็ได้เวลามาเขียนคลาสของชั้นคอนโวลูชันสองมิติขึ้นมา ซึ่งจะคล้ายกับกรณีหนึ่งมิติ แต่จะเพิ่มความซับซ้อนขึ้นมาอีกขั้น

เช่นเคย ก่อนอื่นให้ทำการเรียกคลาสที่จำเป็นต้องใช้ในบทนี้จาก unagi.py พร้อมทั้ง numpy

import numpy as np
from unagi import Chan,Param

โค้ดเขียนคลาสคอนโวลูชันสองมิติ

class Conv2d(Chan):
    def __init__(self,m0,m1,kk,st=1,pad=0,sigma=1):
        '''
        m0 : จำนวนช่องขาเข้า
        m1 : จำนวนช่องขาออก
        kk : ความสูงและความกว้างของตัวกรอง
        st : ความสูงและกว้างที่เลื่อน
        pad : ขอบที่เติมตามแนวความสูงและกว้าง
        sigma : ส่วนเบี่ยงเบนมาตรฐานของค่าสุ่มเริ่มต้นของพารามิเตอร์น้ำหนัก
        
        '''
        # kk,st,pad นั้นควรเป็นลิสต์ของสองค่า แต่หากใส่ค่าเดียวมาให้ทำเป็นเท่ากันทั้งสองมิติ
        if(type(kk)==int):
            kk = [kk,kk] 
        if(type(st)==int):
            st = [st,st]
        if(type(pad)==int):
            pad = [pad,pad]
        
        # พารามิเตอร์ตัวแรกคือน้ำหนักในแต่ละช่อง มีจำนวน [m1,m0,kk[1],k[0]]
        # อีกตัวคือไบแอส มีจำนวนเป็น m1 ให้เริ่มต้นจาก 0
        self.param = [Param(np.random.normal(0,sigma,[m1,m0,kk[1],kk[0]])),
                      Param(np.zeros(m1))]
        self.st = st
        self.pad = pad
    
    def pai(self,X):
        px,py = self.pad
        stx,sty = self.st
        # เติมขอบ ถ้า pad>0
        X = np.pad(X,[(0,0),(0,0),(py,py),(px,px)],'constant')
        # ขนาดในแต่ละมิติของพารามิเตอร์ w (จำนวนช่องขาออก, จำนวนช่องขาเข้า, ความสูงตัวกรอง, ความยาวตัวกรอง)
        m1,m0,kky,kkx = self.param[0].kha.shape
        # ขนาดของข้อมูลขาเข้า (จำนวนข้อมูล, จำนวนช่องขาเข้า, ความสูงตัวกรองหลังเติมขอบ, ความกว้างตัวกรองหลังเติมขอบ)
        n,m0_,ky0,kx0 = X.shape
        # จำนวนช่องของข้อมูลขาเข้าควรเท่ากับจำนวนช่องของพารามิเตอร์ w ขาเข้า
        assert m0_==m0
        # ความสูงข้อมูลขาออก
        kx1 = int((kx0-kkx)/stx)+1
        # ความกว้างข้อมูลขาออก
        ky1 = int((ky0-kky)/sty)+1
        # สร้างอาเรย์ของข้อมูลขาเข้าที่ปรับรูปใหม่เพื่อให้ทำการคำนวณสะดวก
        X_ = np.zeros([n,m0,kky,kkx,ky1,kx1])
        for _j in range(kky):
            j_ = _j+ky1*sty
            for _i in range(kkx):
                i_ = _i+kx1*stx
                X_[:,:,_j,_i,:,:] = X[:,:,_j:j_:sty,_i:i_:stx]
        X_ = X_.transpose(0,4,5,1,2,3).reshape(-1,m0*kkx*kky)
        w = self.param[0].kha.reshape(m1,-1).T
        b = self.param[1].kha
        a = np.dot(X_,w) + b
        a = a.reshape(n,ky1,kx1,-1).transpose(0,3,1,2)
        self.ruprang = n,m1,m0,kky,kkx,ky0,kx0,ky1,kx1
        self.X_ = X_
        return a
    
    def yon(self,g):
        px,py = self.pad
        stx,sty = self.st
        # จำนวนข้อมูล, จำนวนช่องขาเข้า, จำนวนช่องขาออก, ความสูงตัวกรอง, ความกว้างตัวกรอง, ความสูงข้อมูลขาเข้า, ความกว้างข้อมูลขาเข้า, ความสูงข้อมูลขาออก, ความกว้างข้อมูลขาออก
        n,m1,m0,kky,kkx,ky0,kx0,ky1,kx1 = self.ruprang
        g = g.transpose(0,2,3,1).reshape(-1,m1)
        w = self.param[0].kha.reshape(m1,-1).T
        self.param[0].g = np.dot(self.X_.T,g).transpose(1,0).reshape(m1,m0,kky,kkx)
        self.param[1].g = g.sum(0)
        gX_ = np.dot(g,w.T)
        gX_ = gX_.reshape(-1,ky1,kx1,m0,kky,kkx).transpose(0,3,4,5,1,2)
        gX = np.zeros([n,m0,ky0+2*py,kx0+2*px])
        for _j in range(kky):
            j_ = _j+ky1*sty
            for _i in range(kkx):
                i_ = _i+kx1*stx
                gX[:,:,_j:j_:sty,_i:i_:stx] += gX_[:,:,_j,_i,:,:]
        return gX[:,:,py:ky0-py,px:kx0-px]

การเขียนคลาสของชั้นบ่อรวมสูงสุดสองมิติ

เช่นเดียวกับกรณีหนึ่งมิติ สำหรับสองมิติเองก็ต้องมีการใช้ชั้นบ่อรวมสูงสุดเช่นกัน ซึ่งก็เขียนคล้ายกับกรณีหนึ่งมิติ แต่เพิ่มความซับซ้อนขึ้น

import numpy as np
import matplotlib.pyplot as plt
from unagi import Chan,Param

class MaxP2d(Chan):
    def __init__(self,kk,st=None):
        '''
        kk : ความยาวตัวกรอง
        st : ความยาวการเลื่อน (ถ้าไม่กำหนด ก็ให้เท่ากับความยาวตัวกรอง)
        '''
        if(type(kk)==int):
            self.kk = [kk,kk]
        else:
            self.kk = kk
        
        if(st==None):
            self.st = self.kk
        elif(type(st)==int):
            self.st = [st,st]
        else:
            self.st = st
    
    def pai(self,X):
        stx,sty = self.st
        kkx,kky = self.kk
        # ขนาดของข้อมูลขาเข้า (จำนวนข้อมูล, จำนวนช่องขาเข้า, ความสูงข้อมูลขาเข้า, ความกว้างข้อมูลขาเข้า)
        n,m,ky0,kx0 = X.shape
        kx1 = int((kx0-kkx)/stx)+1
        ky1 = int((ky0-kky)/sty)+1
        X_ = np.zeros([n,m,kky,kkx,ky1,kx1])
        for _j in range(kky):
            j_ = _j+ky1*sty
            for _i in range(kkx):
                i_ = _i+kx1*stx
                X_[:,:,_j,_i,:,:] = X[:,:,_j:j_:sty,_i:i_:stx]
        X_ = X_.transpose(0,4,5,1,2,3).reshape(-1,kkx*kky)
        self.argmax = X_.argmax(1)
        self.ruprang = n,m,ky0,kx0,ky1,kx1
        return X_.max(1).reshape(n,ky1,kx1,m).transpose(0,3,1,2)
    
    def yon(self,g):
        g = g.transpose(0,2,3,1)
        stx,sty = self.st
        kkx,kky = self.kk
        # ขนาดของข้อมูลขาเข้า (จำนวนข้อมูล, จำนวนช่องขาเข้า, ความสูงข้อมูลขาเข้า, ความกว้างข้อมูลขาเข้า, ความสูงข้อมูลขาออก, ความกว้างข้อมูลขาออก)
        n,m,ky0,kx0,ky1,kx1 = self.ruprang
        gX_ = np.zeros([g.size,kkx*kky])
        gX_[np.arange(self.argmax.size),self.argmax.flatten()] = g.flatten()
        gX_ = gX_.reshape(-1,ky1,kx1,m,kky,kkx).transpose(0,3,4,5,1,2)
        gX = np.zeros([n,m,ky0,kx0])
        for _j in range(kky):
            j_ = _j+ky1*sty
            for _i in range(kkx):
                i_ = _i+kx1*stx
                gX[:,:,_j:j_:sty,_i:i_:stx] += gX_[:,:,_j,_i,:,:]
        return gX

ตัวอย่างการสร้างและใช้งานโครงข่ายประสาทแบบคอนโวลูชันสองมิติ

เมื่อได้คลาสของชั้นคอนโวลูชันสองมิติและชั้นบ่อรวมสูงสุดสองมิติมาแล้ว ต่อมาจะลองนำมาใช้เพื่อสร้างคลาสของโครงข่ายประสาทขึ้น

คลาสของชั้นต่างๆที่จำเป็น รวมทั้งชั้นคอนโวลูชันสองมิติกับชั้นบ่อรวมสูงสุดสองมิติที่เพิ่งสร้างมาก็ได้ใส่รวมไว้ใน unagi.py แล้ว ทั้งหมด import จากในนั้นมาใช้ได้

เป้าหมายคราวนี้คือข้อมูลรูปร่างต่างๆ ดังที่แสดงในตัวอย่างภาพด้านบน

รูปขาวดำ ขนาด 25×25 แบ่งเป็น 5 กลุ่ม กลุ่มละ 1000 มีรวมทั้งหมด 5000 ภาพ
>> ruprang-raisi-25x25x1000x5.rar

รูปสี ขนาด 25×25 แบ่งเป็น 6 กลุ่ม กลุ่มละ 1000 มีรวมทั้งหมด 6000 ภาพ
>> ruprang-misi-25x25x1000x6.rar

ในที่นี้จะสร้างเป็นคลาสของโครงข่ายประสาทแบบคอนโวลูชันสองมิติที่มีโครงสร้างภายในตายตัวเป็นชั้นคอนโวลูชัน 2 ชั้น และชั้นเชิงเส้น 2 ชั้น

ชั้นที่ 1 ข้อมูลขาออก 32 ช่อง ขนาดตัวกรอง 2×2

ตามด้วยชั้นที่ 2 ข้อมูลขาออก 32 ช่อง ขนาดตัวกรอง 3×3

จำนวนช่องข้อมูลขาเข้านั้นให้กำหนดได้อิสระ ถ้าเป็นภาพขาวดำก็มี 1 ช่อง ภาพเป็นภาพสีก็มี 3 ช่อง

ตัวอย่างที่จะใช้ในที่นี้มีขนาด 25×25 ดังนั้นเมื่อผ่านตัวกรองขนาด 2×2 แล้วตามด้วยบ่อรวมสูงสุด 2×2 อีกก็จะกลายเป็น (25-2+1)/2 × (25-2+1)/2 = 12×12

จากนั้นในชั้นที่ 2 เมื่อเมื่อผ่านตัวกรองขนาด 3×3 แล้วตามด้วยบ่อรวมสูงสุด 2×2 อีกก็จะกลายเป็น (12-3+1)/2 × (12-3+1)/2 = 5×5

ข้อมูลที่ออกจากชั้นคอนโวลูชันนี้มีขนาด 5×5 และมี 32 ช่อง ดังนั้นจำนวนเซลล์ขาเข้าของชั้นเชิงเส้นที่จะตามมาก็จะต้องเป็น 5×5×32=800

จากนั้นให้จำนวนข้อมูลขาออกของชั้นเชิงเส้นชั้นแรก (ชั้นที่ 3) เป็น 64 และชั้นถัดมา (ชั้นที่ 4) เป็นเท่ากับจำนวนกลุ่มของคำตอบที่ต้องการแบ่ง ซึ่งในที่นี้ให้กำหนดได้อิสระ

คลาสเขียนขึ้นมาได้ดังนี้

import numpy as np
import matplotlib.pyplot as plt
from unagi import Affin,Relu,Softmax_entropy,ha_1h,Adam,Conv2d,Plianrup,MaxP2d

class PrasatConvo2D:
    def __init__(self,c0,n,eta):
        '''
        c0: จำนวนช่องขาเข้า
        n: จำนวนกลุ่มของคำตอบ
        eta: อัตราการเรียนรู้
        '''
        self.chan = []
        # ชั้น 1 คอนโวลูชัน (ช่องขาเข้า c0, ช่องขาออก 32, ขนาดตัวกรอง 2×2)
        self.chan.append(Conv2d(c0,32,[2,2],[1,1],[0,0],sigma=1))
        self.chan.append(Relu())
        self.chan.append(MaxP2d(2)) # ชั้นบ่อรวมสูงสุด
        # ชั้น 2 คอนโวลูชัน (ช่องขาเข้า 32, ช่องขาออก 32, ขนาดตัวกรอง 3×3)
        self.chan.append(Conv2d(32,32,[3,3],[1,1],[0,0],sigma=1))
        self.chan.append(Relu())
        self.chan.append(MaxP2d(2)) # ชั้นบ่อรวมสูงสุด
        # ชั้นเปลี่ยนรูปก่อนเข้าสู่ชั้นเชิงเส้น
        self.chan.append(Plianrup(-1))
        # ชั้น 3 เชิงเส้น (เซลล์ขาเข้า 800, เซลล์ขาออก 64)
        self.chan.append(Affin(800,64,np.sqrt(2./800)))
        self.chan.append(Relu())
        # ชั้น 4 (เซลล์ขาเข้า 64, เซลล์ขาออก n)
        self.chan.append(Affin(64,n,np.sqrt(2./64)))
        self.chan.append(Softmax_entropy())
        
        self.opt = Adam(self.param(),eta=eta)
        
        self.n = n
    
    def rianru(self,X,z,X_truat,z_truat,n_thamsam=100,n_batch=50,ro=0):
        n = len(z)
        Z = ha_1h(z,self.n)
        self.entropy = []
        self.khanaen_fuek = []
        self.khanaen_truat = []
        khanaen_sungsut = 0
        for o in range(n_thamsam):
            lueak = np.random.permutation(n)
            for i in range(0,n,n_batch):
                Xb = X[lueak[i:i+n_batch]]
                Zb = Z[lueak[i:i+n_batch]]
                entropy = self.ha_entropy(Xb,Zb)
                entropy.phraeyon()
                self.opt()
            entropy,khanaen_fuek = self.ha_entropy(X_fuek,Z,ao_khanaen=1)
            khanaen_truat = self.ha_khanaen(X_truat,z_truat)
            self.entropy.append(entropy.kha)
            self.khanaen_fuek.append(khanaen_fuek)
            self.khanaen_truat.append(khanaen_truat)
            print('รอบที่ %d. เอนโทรปี=%.3e, ทำนายข้อมูลฝึกแม่น=%.3f, ทำนายข้อมูลตรวจสอบแม่น=%.3f'%(o,entropy.kha,khanaen_fuek,khanaen_truat))
            
            if(khanaen_truat>khanaen_sungsut):
                khanaen_sungsut = khanaen_truat
                maiphoem = 0
            else:
                maiphoem += 1
            
            if(ro>0 and maiphoem>=ro):
                break
    
    def ha_entropy(self,X,Z,ao_khanaen=0):
        for c in self.chan[:-1]:
            X = c(X)
        if(ao_khanaen):
            return self.chan[-1](X,Z),(X.kha.argmax(1)==Z.argmax(1)).mean()
        return self.chan[-1](X,Z)
    
    def ha_khanaen(self,X,z):
        return (self.thamnai(X)==z).mean()
    
    def param(self):
        p = []
        for c in self.chan:
            if(hasattr(c,'param')):
                p.extend(c.param)
        return p
    
    def thamnai(self,X):
        for c in self.chan[:-1]:
            X = c(X)
        return X.kha.argmax(1)

เริ่มจากลองนำมาใช้แบ่งกลุ่มข้อมูลภาพขาวดำ

from glob import glob

X = np.array([plt.imread(x) for x in sorted(glob('ruprang-raisi-25x25x1000x5/*/*.png'))]) # โหลดภาพขาวดำ
X = X.reshape(-1,1,25,25) # แปลงรูป ให้มีมิติของจำนวนช่องซึ่งเป็น 1
z = np.arange(5).repeat(1000) # คำตอบ เป็นเลข 0,1,2,3,4
np.random.seed(0)
sumlueak = np.random.permutation(5000) # สุ่มสลับลำดับ
# ข้อมูลมี 5000 ภาพ ในที่นี้แบ่งให้เป็นข้อมูลฝึก 4000 ภาพ ข้อมูลตรวจสอบ 1000 ภาพ
X_fuek,X_truat = X[sumlueak[:4000]],X[sumlueak[4000:]]
z_fuek,z_truat = z[sumlueak[:4000]],z[sumlueak[4000:]]
# สร้างโครงข่าย จำนวนช่องขาเข้าเป็น 1 เพราะเป็นภาพขาวดำ ส่วนคำตอบมี 5 กลุ่ม
prasat = PrasatConvo2D(1,5,eta=0.005)
prasat.rianru(X_fuek,z_fuek,X_truat,z_truat,n_thamsam=200,n_batch=64,ro=20)
# วาดกราฟแสดงเอนโทรปีและคะแนนสำหรับข้อมูลฝึกและข้อมูลตรวจสอบ
plt.figure(figsize=[5,7],dpi=100)
plt.subplot(211)
plt.semilogy()
plt.plot(prasat.entropy,'b')
plt.title('เอนโทรปี',family='Tahoma',size=14)
plt.grid(ls='--')

plt.subplot(212)
plt.plot(prasat.khanaen_fuek,'m',label='ข้อมูลฝึก')
plt.plot(prasat.khanaen_truat,'g',label='ข้อมูลตรวจสอบ')
plt.grid(ls='--')
plt.title('คะแนน',family='Tahoma',size=14)
plt.legend(prop={'family':'Tahoma','size':14})

plt.tight_layout()
plt.show()

หลังจากรันไปแล้วต้องรอนานหน่อย เนื่องจากข้อมูลจำนวนมากและโครงข่ายประสาทเทียมแบบคอนโวลูชันนั้นค่อนข้างจะกินเวลาในการคำนวณ

สุดท้ายแล้วก็จะได้ผลออกมาดังนี้



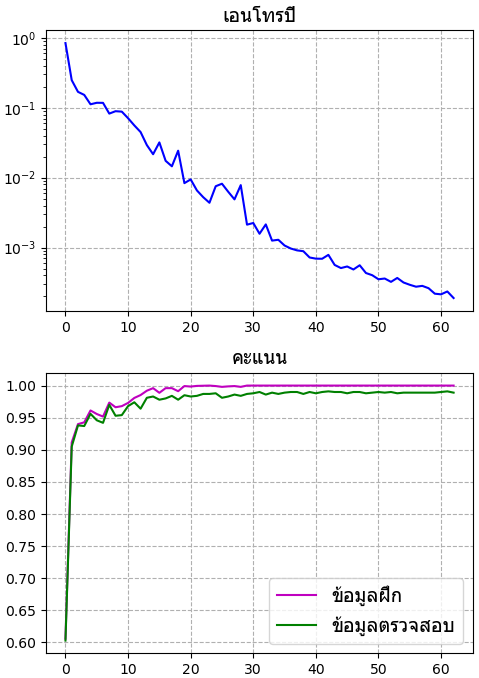
จะเห็นว่าเมื่อฝึกไปแล้วก็จะสามารถทำนายข้อมูลได้แม่นยำเป็นอย่างดีทั้งชุดข้อมูลฝึกและข้อมูลทดสอบ แม้ว่าอาจจะยังทำนายข้อมูลทดสอบได้ไม่ถูกต้องบางส่วนอยู่ แต่ก็ถือว่าเกือบ 100%



จากนั้นมาดูอีกตัวอย่าง คราวนี้มาใช้กับภาพสี ข้อแตกต่างคือโครงสร้างของโครงข่าย ให้มีข้อมูลขาเข้าเป็น 3 ช่อง และขาออกเป็น 6 ตัว นอกนั้นโดยรวมแล้วก็เหมือนเดิม

X = np.array([plt.imread(x) for x in sorted(glob('ruprang-misi-25x25x1000x6/*/*.png'))]) # โหลดภาพสี
X = X.transpose(0,3,1,2)[:,:3] # ภาพที่โหลดมาจะมีมิติของสีสามสีเป็นมิติที่ 4 ให้ทำการสลับเอามิติของสีมาไว้เป็นมิติที่ 2
z = np.arange(6).repeat(1000) # เลขบอกกลุ่ม 0,1,2,3,4,5
np.random.seed(0)
sumlueak = np.random.permutation(6000) # สุ่มสลับลำดับ
# แบ่งข้อมูล 6000 ภาพเป็นข้อมูลฝึก 4800 ภาพ ข้อมูลทดสอบ 1200 ภาพ
X_fuek,X_truat = X[sumlueak[:4800]],X[sumlueak[4800:]]
z_fuek,z_truat = z[sumlueak[:4800]],z[sumlueak[4800:]]
# สร้างโครงข่าย จำนวนช่องขาเข้าเป็น 3 เพราะเป็นภาพสี ส่วนคำตอบมี 6 กลุ่ม
prasat = PrasatConvo2D(3,6,eta=0.005)
prasat.rianru(X_fuek,z_fuek,X_truat,z_truat,n_thamsam=200,n_batch=64,ro=20)
# วาดกราฟแสดงเอนโทรปีและคะแนนสำหรับข้อมูลฝึกและข้อมูลตรวจสอบ
plt.figure(figsize=[5,7],dpi=100)
plt.subplot(211)
plt.semilogy()
plt.plot(prasat.entropy,'b')
plt.title('เอนโทรปี',family='Tahoma',size=14)
plt.grid(ls='--')

plt.subplot(212)
plt.plot(prasat.khanaen_fuek,'m',label='ข้อมูลฝึก')
plt.plot(prasat.khanaen_truat,'g',label='ข้อมูลตรวจสอบ')
plt.grid(ls='--')
plt.title('คะแนน',family='Tahoma',size=14)
plt.legend(prop={'family':'Tahoma','size':14})

plt.tight_layout()
plt.show()

ผลที่ได้



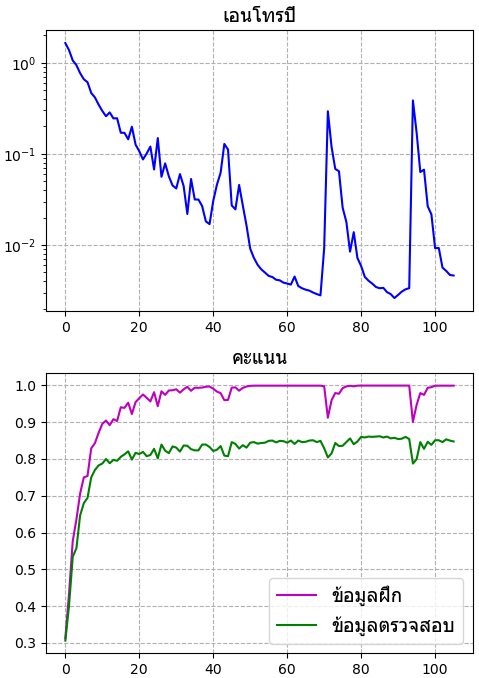
จะเห็นว่าสำหรับภาพสีนั้นค่อนข้างจะยากกว่า ผลที่ออกมาได้จึงอาจไม่ดีเท่า ข้อมูลตรวจสอบทำนายได้ถูกต้องอยู่แค่ที่ประมาณ 85%

ในที่นี้เป็นแค่ตัวอย่างที่กำหนดโครงสร้างขึ้นมาแบบง่ายๆ ไม่ได้ปรับแต่งอะไรมาก อาจลองปรับปรุงผลให้ดีขึ้นได้โดยปรับโครงสร้างของโครงข่ายดูเช่นเพิ่มจำนวนชั้น หรือปรับขนาดตัวกรองหรือจำนวนช่อง หรือใส่ชั้นดรอปเอาต์ หรือแบตช์นอร์ม แล้วเทียบผลที่ได้ดู




สรุปส่งท้ายบท

ในบทนี้ได้แสดงวิธีการสร้างโครงข่ายประสาทเทียมแบบคอนโวลูชันสองมิติ ซึ่งมีโครงสร้างที่ซับซ้อนแต่ถูกใช้อย่างกว้างขวาง

ในที่นี้จะไม่เขียนถึงคอนโวลูชันสามมิติขึ้นไป ซึ่งอาจใช้กับข้อมูลพวกภาพวีดีโอ ซึ่งเป็นภาพที่มีมิติเวลาเพิ่มเข้ามาอีก แต่เมื่อเข้าใจหลักการของแบบสองมิติแล้ว ก็สามารถต่อยอดได้

หากใช้ pytorch ก็มีชั้นคอนโวลูชันสามมิติเตรียมไว้ให้ สามารถใช้ได้ทันที (ลองดูใน pytorch เบื้องต้น บทที่ ๑๒)

เนื้อหาในที่นี้จะจบลงตรงที่โครงข่ายประสาทเทียมแบบคอนโวลูชันสองมิติเพียงเท่านี้ แต่ยังมีเนื้อหาในส่วนลึกลงไปอีกมากมายที่ไม่ได้กล่าวถึง ซึ่งสามารถไปศึกษาเพิ่มเติมต่อไปได้

นอกจากนี้แล้วยังมีโครงข่ายประสาทเทียมอีกหลายรูปแบบซึ่งจะใช้กับงานเฉพาะทางมากขึ้น ดังนั้นจึงอาจไปศึกษาต่อในส่วนของโครงข่ายแบบที่เหมาะกับงานที่ต้องการไปทำต่อไป

~ 自己紹介 ~

目次

日本による名言集

python モジュール -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 機械学習 -- ニューラル      ネットワーク

javascript

モンゴル語

言語学

maya

確率論

日本での日記

中国での日記 -- 北京での日記 -- 香港での日記 -- 澳門での日記

台灣での日記

北欧での日記

他の国での日記

qiita

その他の記事

記事の類別

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --sql --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา บันทึก เรื่องแต่ง ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม

　 記事を検索

　 最新記事

　 おすすめの記事

月別記事

もっと前の記事

ไทย

日本語

中文